第 3 章算法分析

有一个经典的故事，国王委托著名的数学家阿基米德判断黄金王冠是否如声称的那样是纯金的而没有掺白银。当阿基米德进入浴盆洗澡时，他发现了一个解决方法。他注意到，自己身体进入浴盆的体积与水溢出浴盆的数量成比例。这给了阿基米德启示，他立刻跳出浴盆，赤裸着身体奔跑在大街上大喊＂找到了！找到了！＂。他发现了一个分析工具（排水量）。只要用一个简单的天平，就可以判断国王的新王冠是不是纯金的。具体做法就是：阿基米德把王冠和同等质量的黄金分别沉到一碗水里，观察两者的排水最是否一样。这个发现对金匠来说是不幸的，因为如果阿基米德进行分析后，发现王冠溢出的水比同等质量的纯金块所溢出的水多，那就意味着王冠不是纯金的。

在本书中，我们对设计“优秀”的数据结构和算法感兴趣。简言之，数据结构是组织和访问数据的一种系统化方式，算法是在有限的时间里一步步执行某些任务的过程。这些概念对计算极为重要，为了分辨哪些数据结构和算法是“优秀” 的，我们需要一些精确分析算法的方法。

我们在本书中用到的主要分析方法包括算法和数据结构的运行时间和空间利用表示。运行时间是一个很好的度量，因为时间是宝贵的资源一计算机解决方案应该运行得尽可能快。一般来说，一个算法或数据结构操作的运行时间随着输入大小而增加，尽管它可能对相同大小的不同输入也有所变化。另外，运行时间也受硬件环境（例如，处理器、时钟频率、内存、硬盘）以及算法实施和执行的软件环境（例如，操作系统、程序设计语言）的影响。当其他所有因素不变时，如果计算机有更快的处理器，或者程序编译到本机代码来执行而不是解释执行，有相同输入数据的相同算法的运行时间会更少。我们将在本章的开始部分讨论进行实验研究的工具，并讨论将其作为评估算法效率的一种主要方法的局限性。

要研究运行时间这一度量，要求我们会用一些数学工具。尽管可能存在来自不同环境因素的干扰，但是我们主要关注算法的运行时间和其输入大小的关系。我们希望将算法的运行时间表示为输入大小的函数。但是，度量它的合适途径是什么？在本章中，我们将自己动手开发一种分析算法的数学方法。

3.1 实验研究¶

如果算法已经实现了，我们可以通过在不同的输入下执行它并记录每一次执行所花费的时间来研究它的运行时间。python 中一个简单的实现方法是使用 time 模块的 time()函数。这个函数传递的是自新纪元基准时间后已经过去的秒数或分数（新纪元是指 1970 年）。当我们可以通过记录算法运行前的那一刻以及算法执行完毕后的那一刻，并且计算它们之间的差（如下所示）来判定消逝的时间时，新纪元的选择不影响测试时间的结果。

from time import time
start_t ime = time() # record the starting time
run algorithm
end_time = time() # record the ending time
elapsed = end_time - start_time # compute the elapsed time

在第 5 章，我们将演示这种方法的使用，即在 python list 类的效率上收集实验数据。用这样的方法测量消逝的时间很好地反映了算法效率，但绝不意味着完美。time() 函数的测量是相对于“挂钟＂的。因为许多进程共享使用计算机的中央处理器(CPU) ，所以算法执行过程花费的时间依赖于在作业执行时正运行在计算机上的其他进程。一个更公正的度量是算法使用的 CPU 周期的数量。即使用相同的输入重复相同的算法可能没有保持一致性，也要使用 time 模块的 clock() 函数，并且它的粒度依赖于计算机系统。python 包含了一个更高级的模块（名叫 timeit) ，它可以自动地做多次重复实验来评估差异。

通常我们认为运行时间依赖于输入的大小和结构，所以应该在各种大小的不同测试输入上执行独立实验。接下来我们可以通过绘制算法每次运行的性能图来可视化结果， x 坐标表示输入大小 n,y 坐标表示运行时间 t。图 3-1 显示了这样的假设性数据。这种可视化可以提供关于算法的问题大小和执行时间的直观描述。这可用于对实验数据做统计分析，以寻找符合实验数据的最好的输入大小函数。为了使得分析更有意义，要求选择好的样本输入并且对其进行足够多次的测试，使算法运行时间的统计更准确。

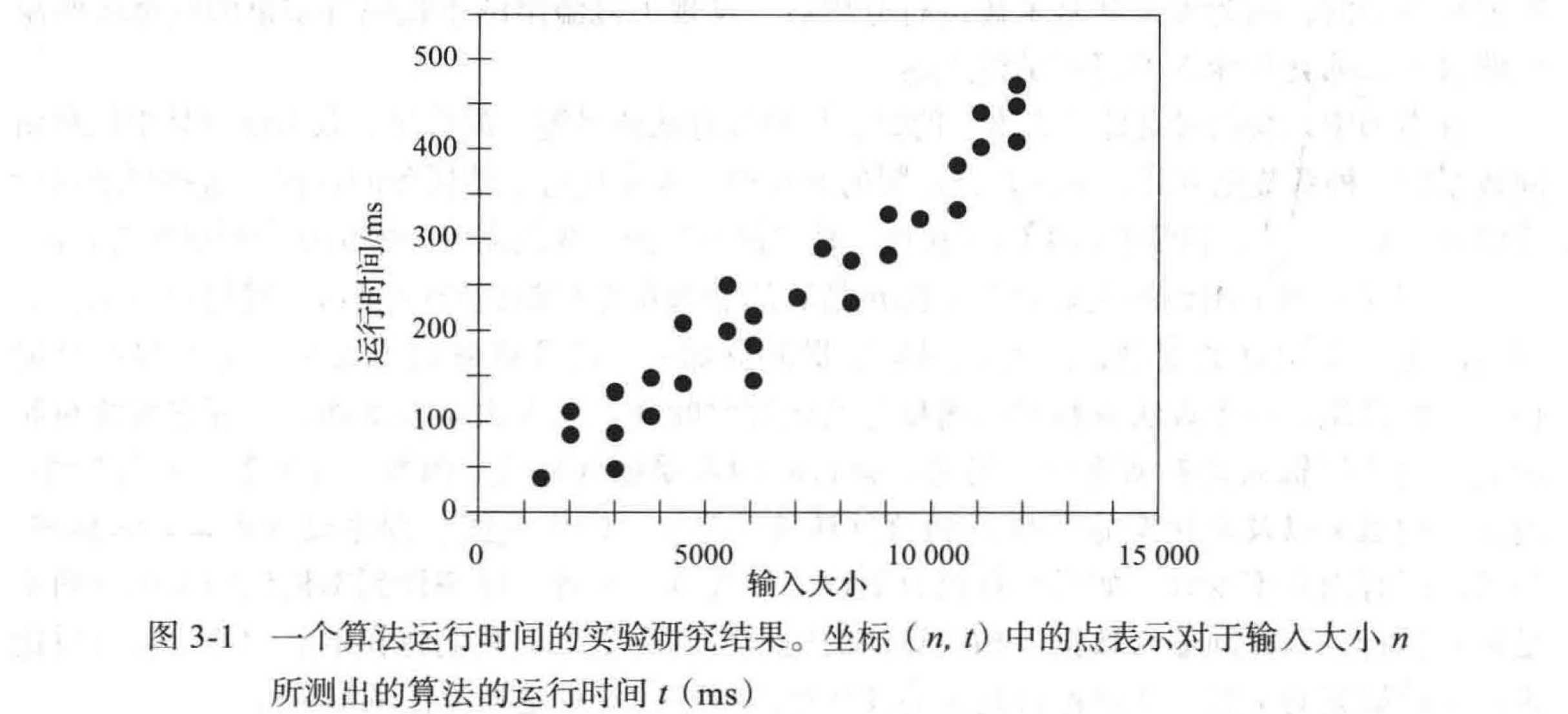
实验分析的挑战¶

虽然执行时间的实验研究是有用的，但是使用这样的算法分析有 3 个主要的局限性（尤其是在优化生产质量代码时）：

很难直接比较两个算法的实验运行时间，除非实验在相同的硬件和软件环境中执行。
实验只有在有限的一组测试输入下才能完成，因此它们忽略了不包括在实验中的输入的运行时间（这些输入可能是重要的）。
为了在实验上执行算法来研究它的执行时间，算法必须完全实现。

最后一个要求是实验研究应用中最严重的缺点。在设计的初期，当考虑数据结构或算法的选择时，花费大量的时间实现一个显然低劣的算法是不明智的。

进—步的实验分析¶

我们的目标是开发一种分析算法效率的方法：

在软硬件环境独立的情况下，在某种程度上允许我们评价任意两个算法的相对效率。

2) 通过研究不需要实现的高层次算法描述来执行算法。 3) 考虑所有可能的输入。

计算原子操作¶

为了在没有执行实验时分析一个算法的执行时间，我们用一个高层次的算法描述直接进行分析（可以是真实的代码片段，也可以是独立于语言的伪代码）。我们定义了一系列原子操作，如下所示：

给对象指定一个标识符
确定与这个标识符相关联的对象
执行算术运算（例如，两个数相加）
比较两个数的大小
通过索引访问 python 列表的一个元素
调用函数（不包括函数内的操作执行）
从函数返回

从形式上说， 一个原子操作相当于一个低级别指令，其执行时间是常数。理想情况下，这可能是被硬件执行的基本操作类型，尽管许多原子操作可能被转换成少量的指令。我们并不是试着确定每一个原子操作的具体执行时间，而是简单地计算有多少原子操作被执行了，用数字 t 作为算法执行时间的度量。

操作的计数与特定计算机中真实的运行时间相关联，每个原子操作相当于固定数量的指令，并且该操作只有固定数量的原子操作。这个方法中的隐含假设是不同原子操作的运行时间是非常相似的。因此算法执行的原子操作数 t 与算法的真实运行时间成正比。

随着输入函数的变化进行测量操作¶

为了获取一个算法运行时间的增长情况，我们把每一个算法和函数 $f(n)$ 联系起来，其中把执行的原子操作的数量描述为输入大小 n 的函数 $f(n)$ 。3.2 节将会介绍 7 个最常见的函数。3.3 节将介绍一个函数之间相互比较的数学框架。

最坏情况输入的研究¶

对于相同大小的输入，算法针对某些输入的运行速度比其他的更快。因此，我们不妨把算法的运行时间表示为所有可能的相同大小输入的平均值的函数。不幸的是，这样的平均情况分析是相当具有挑战性的。它要求定义一组输入的概率分布，这通常是一个困难的工作。图 3 -2 表明，根据输入分布，算法的运行时间可以在最坏和最好情况运行时间之间的任何地方。例如，假设实际上输入只有 “A" 或 “ D " 类型将会怎么样？

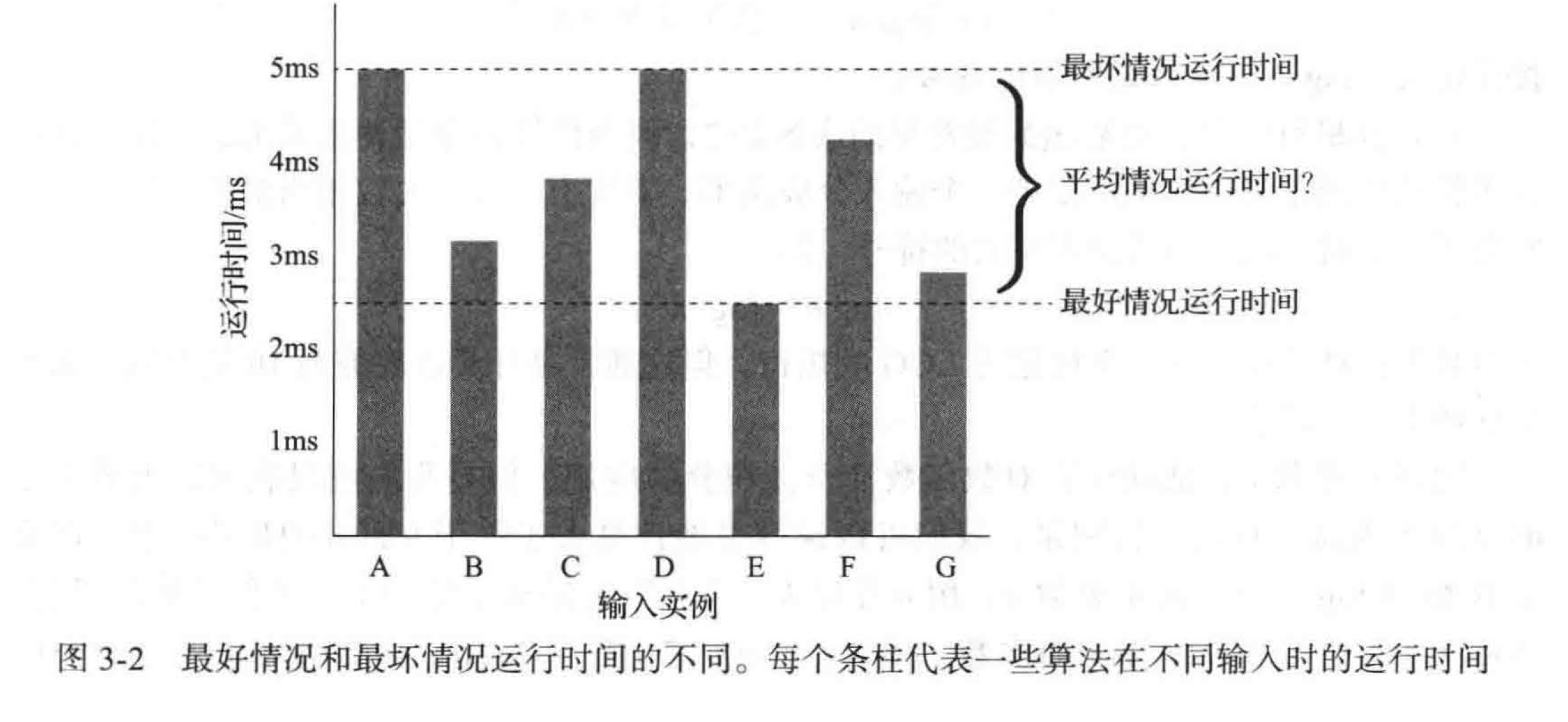
平均情况分析通常要求计算基于给定输入分布的预期运行时间，这通常涉及复杂的概率理论。因此，在本书的其余部分，除非特别指明，一般我们都按照最坏情况把算法的运行时间表示为输入大小 n 的函数。

最坏情况分析比平均情况分析容易很多，它只需要有识别最坏情况输入的能力，这通常是很简单的。另外，这个方法通常会导出更好的算法。算法在最坏情况下很好执行的标准必然是该算法在每一个输入情况都能很好地执行。也就是说，最坏情况的设计会使得算法更加健壮，这很像一个飞毛腿总是在斜坡上练习跑步。

3.2 本书使用的 7 种函数¶

在这一节，我们将简要讨论用在算法分析中最重要的 7 种函数。我们把这 7 种简单的函数用在本书的几乎所有分析中。事实上，某些章节使用的函数不同于这 7 种的将会被标记为星号（＊），以表明这是可选的。除了这 7 种基本的函数，附录 B 包含了其他被应用在数据结构和算法分析中的一系列有用的数学定理。

3.2.1 常数函数¶

我们能想起的最简单的函数是常数函数。这个函数是

\[ f(n) = C \]

对一些固定的常数 C, 例如 $c=5 、c=7$ 或 $c = 210$ 。也就是说，对任意参数 n, 常数函数 $f(n)$ 的值都是 c 。换言之， n 的值是什么并不重要， $f(n)$ 总是为定值 $c$

我们对整数函数最感兴趣，因此最基本的常数函数是 $g(n) = 1$ , 这是用在本书中最经典的常数函数。注意，任何其他的函数 $f(n) = c$ 都可以被写成常数 c 乘以 $g(n)$ ，即 $f(n) =cg(n)$ 。

正因为常数函数简单，所以它在算法分析中是很有用的，它描述了在计算机上需要做的基本操作的步数，例如两个数相加、给一些变量赋值或者比较两个数的大小。

3.2.2 对数函数¶

数据结构和算法分析中令人感兴趣甚至惊奇的是无处不在的对数函数， $f(n) = \log_bn$, 常数 $b > 1$ 。此函数定义如下：

\[ x = \log_b n\ \ \ \ 当且仅当 \ b^x= n \]

按照定义， $\log_b1 = 0$ 。b 是对数的底数。

在计算机科学中，对数函数最常见的底数是 2, 因为计算机存储整数采用二进制，并且许多算法中的常见操作是反复把一个输入分成两半。事实上，这个底数相当常见，以至于当底数等于 2 时，我们通常会省略它的符号，即

\[ \log n = \log_2 n \]

大多数手持计算器上有一个标记为 LOG 的按钮，但这通常是计算以底数为 10 的对数，而不是底数为 2 的对数。

对任意整数 n, 准确计算对数函数涉及微积分的应用，但是我们可以利用近似值来足够好地实现这一目的。特别是，我们可以很容易地计算大于等于 $\log_b n$ 的最小整数（即向上取整， $\left \lceil\log_b n \right \rceil$ ）。对正整数 n, 用 n 除以 b, 只有当结果小于等于 1 时才停止除法操作，$\left \lceil\log_b n \right \rceil$ 的值即为 n 除以 b 的次数。例如，$\left \lceil\log_3 27 \right\rceil$ 等于 3，因为 ((27/3)/3)/3 = 1 。

3.2.3 线性函数¶

另一个简单却很重要的函数是线性函数，

\[ f(n) = n \]

即，给定输入值 n, 线性函数 $f$ 就是 $n$ 本身。

这个函数出现在我们必须对所有 n 个元素做基本操作的算法分析的任何时间。例如，比较数字 x 与大小为 n 的序列中的每一个元素，需要做 n 次比较。线性函数也实现了用任何算法处理不在计算机内存中的 n 个对象的最快运行时间，因为读 n 个对象已经需要 n 次操作了。

3.2.4 $n \log n$ 函数¶

接下来要讨论的函数是 $n \log n$ 函数，

\[ f(n) = n \log n \]

对于一个输入值 n, 这个函数是 n 倍的以 2 为底的 n 的对数。这个函数的增长速度比线性函数快，比二次函数慢。因此，与运行时间是二次的算法相比较，我们更喜欢运行时间与 $n \log n$ 成比例的算法。我们会看到一些运行时间与 $n \log n$ 成比例的重要算法。例如，对 n 个任意数进行排序且运行时间与 $n \log n$ 成比例的最快可能算法。

3.2.5 二次函数¶

另一个经常出现在算法分析中的函数是二次函数，

\[ f(n)=n^2 \]

即，给定输入值 $n$ ，函数 $f$ 的值为 $n$ 与自身的乘积（即 “n 的平方”) 。二次函数用在算法分析中的主要原因是，许多算法中都有嵌套循环，其中内层循环执行一个线性操作数，外层循环则表示执行线性操作数的次数。因此，在这个情况下，算法执行了 $n ·n =n^2$ 个操作。

嵌套循环和二次函数¶

二次函数也可能出现在嵌套循环中，第一次循环迭代使用的操作数为 1 ，第二次为 2，第三次为 3，等等。即操作数为

\[ 1 + 2 + 3 + ··· + (n - 2) + (n - 1) + n \]

换言之，如果内层循环的操作数随外层循环的每次迭代逐次加 1 这个函数即表示嵌套循环总的操作数。这个数量也有一个有趣的典故。

1787 年，一个德国教师让 9 ~ 10 岁大的小学生计算从 1 ~ 100 所有整数之和。立刻有一个孩子说自己已经有答案了！老师很怀疑，因为这个孩子的答题板上只有一个答案。但是，他的答案 5050 却是正确的。这个孩子长大后成了那个时代最伟大的数学家之一，他就是卡尔·高斯。我们推测年轻的高斯用了下面的恒等式。

\[ 1 +2+3+ …+ (n-2) +(n - 1)+n=\frac{n(n+1)}2 \]

图 3 -3 中所示即为命题 3-3 的两个“可视化”的证明。

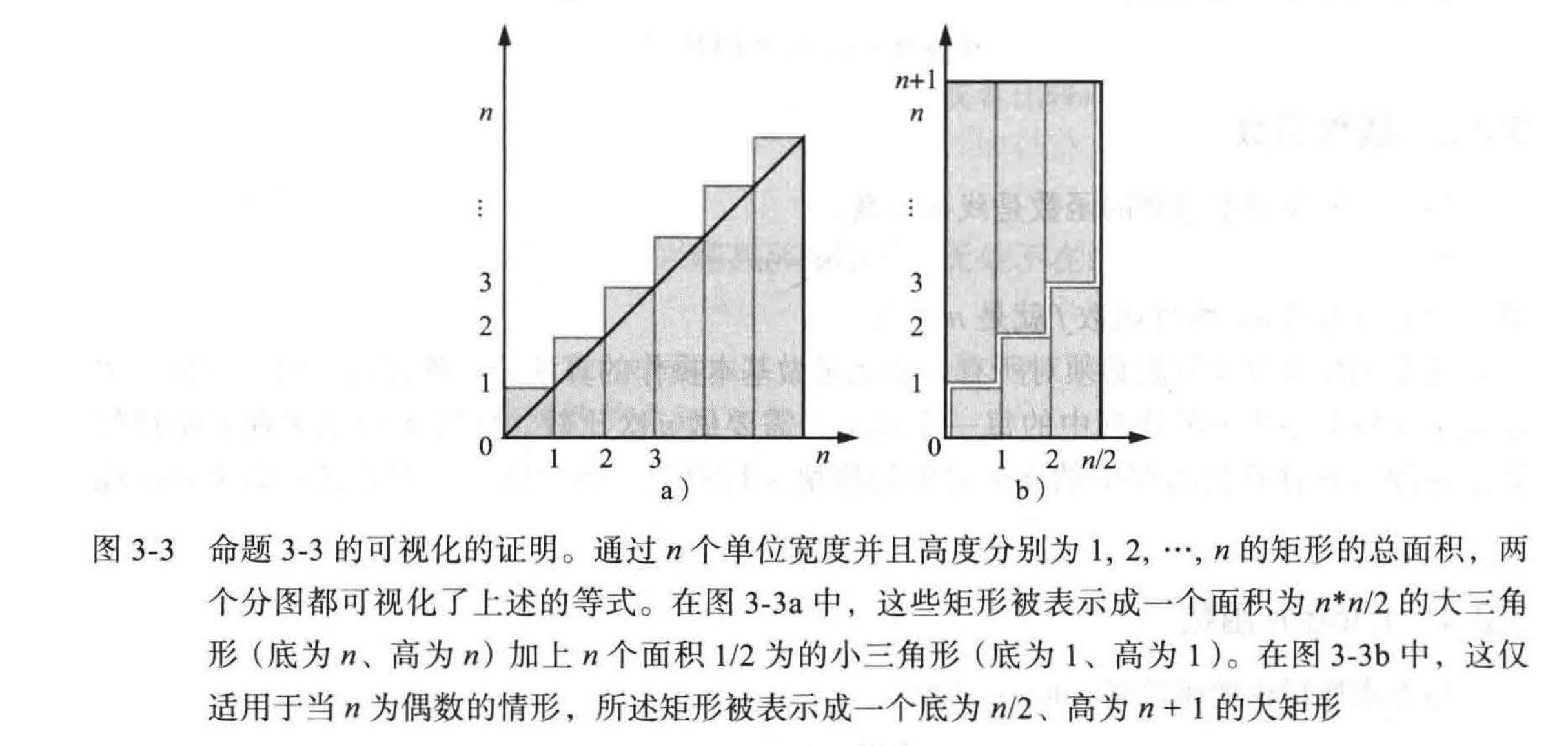
从命题 3-3 得到的结论是，如果我们执行一个含有嵌套循环的算法，那么在内循环中每增加一个操作，执行外循环时操作的总数是 n 的平方。更确切地说，操作的总数是 n*n/2 + n/2, 所以与一个在内循环执行时每次使用 n 个操作的算法相比，这仅仅是这个算法操作总数的一半多一些。但增长的阶数仍然是 n 的平方

3.2.6 三次函数和其他多项式¶

继续我们对函数输入能力的讨论，我们考虑三次函数(cubic function)

\[ f(n)=n^3 \]

这个函数分配一个输入值 n, 可以得到 n 的三次方这样一个输出。与前面提到的常数函数、线性函数和平方函数相比，这个函数在算法分析文章中出现的频率较低，但它确实会时不时地出现。

多项式¶

到目前为止，我们已经列出的大多数函数可以看作一个更大的类函数（多项式）的一部分。一个多项式函数有如下的形式，

\[ f(n) = a_0+a_1n +a_2n^2+ a_3n^3+. .. + a_dn^d \]

其中 $a_0, a_1, …, a_d$ 都是常数，称为多项式的系数，并且整数 $d$ 表示多项式中的最高幕次，称为多项式的次数。

因此，我们可能会质疑，在用于算法分析时本书仅仅提出了 4 个重要的函数，但之所以我们坚持说有 7 个函数，那是因常量函数、线性函数和二次函数太重要而不能与其他多项式放在一起。而且较小次数的多项式的运行时间一般比较大次数的多项式的运行时间要好。

求和¶

在数据结构和算法的分析中一次又一次出现的表示法就是求和，其定义如下：

\[ \sum_{i=a}^{b}f(i)=f(a)+f(a+1)+f(a+2)+...+f(b) \]

其中 a 和 b 都是整数，并且 $a \le b$ 。之所以出现在数据结构与算法分析中，是因为循环的运行时间自然会引起求和。

3.2.7 指数函数¶

用在算法分析中的另一个函数是指数函数，

\[ f(n)=b^n \]

其中 b 是一个正的常数，称为底，参数 n 是指数。也就是说，函数 f(n) 分配给输入参数 n 的值是通过底数 b 乘以它自己 n 次获得的。考虑到对数函数的情况，在算法分析中，指数函数最基本的情况是 b=2 。例如，含有 n 位的整数字可以表示小于 $2^n$ 的所有非负整数。如果通过执行一个操作开始一个循环，然后每次迭代所执行的操作数目翻倍，则在第 n 次迭代所执行的操作数目为 $2^n$ 。

3.2.8 比较增长率¶

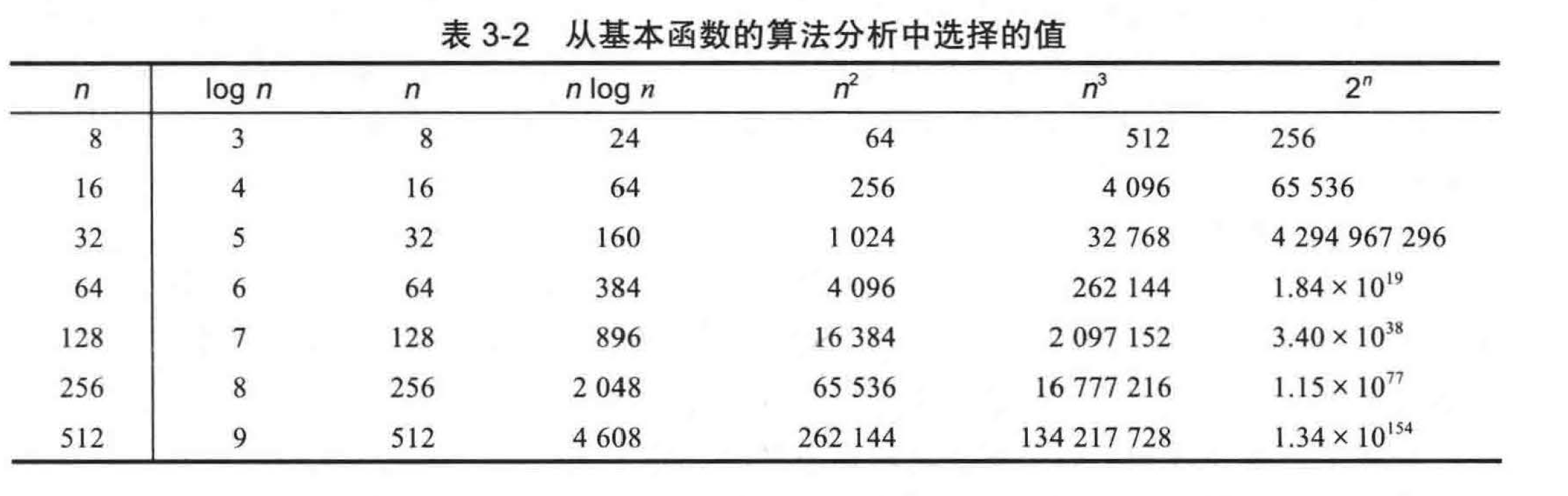
综上所述，按顺序给出的算法分析使用的 7 个常用函数如表 3-1 所示。

理想情况下，我们希望数据结构的操作运行时间与常数函数或者对数函数成正比，而且我们希望算法以线性函数或 $n \log n$ 函数来运行。运行时间为二次或者三次的算法不太实用，除最小输入规模的情况外，运行时间为指数的算法是不可行的。7 个函数的增长率如图 3-4 所示。

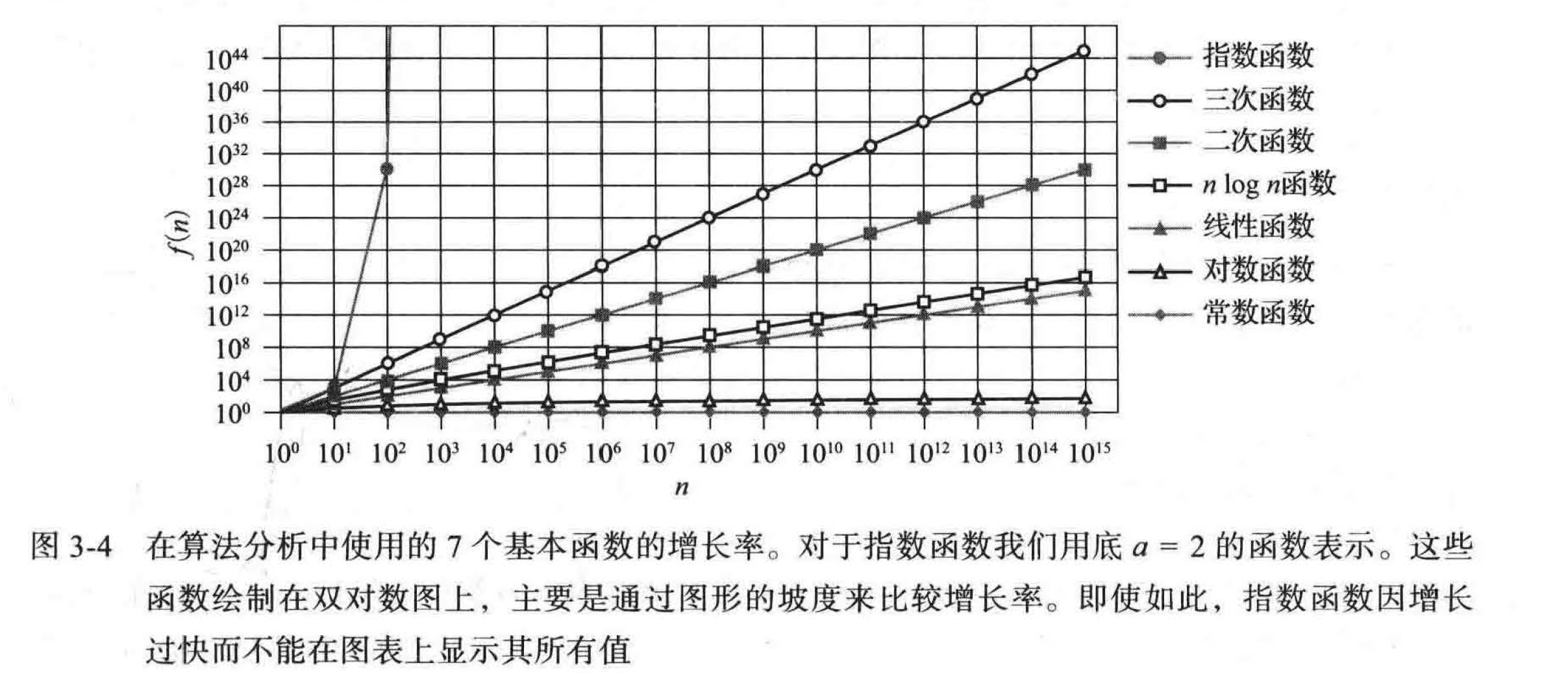
向下取整和向上取整函数¶

以上函数还有一个方面要额外考虑。在讨论到对数时我们指出，对数的值通常不是一个整数，然而一个算法的运行时间通常是通过一个整数来表示的，比如操作的数量。因此，一个算法的分析有时可能涉及向下取整和向上取整函数的使用，它们分别定义如下：

$\left \lfloor x \right \rfloor=$ 小于或者等于 x 的最大整数。
$\left \lceil x \right \rceil=$ 大于或者等于 x 的最小整数。

3.3 渐近分析¶

在算法分析中，我们重点研究运行时间的增长率，采用宏观方法把运行时间视为输入大小为 n 的函数。例如，通常只要知道算法的运行时间为按比例增长到 n 就足够了。

我们用函数的数学符号（不考虑那些不变因子）来分析算法。换句话说，我们这样用函数描述算法的运行时间：输入一个 n 值，对应输出一个数据，用这个数据来反映决定关于 n 的增长率的主要因素。这种方法表明：在伪代码描述或高级语言执行的每一个基本步骤中可以用几个微指令来描述。因此，我们能够通过估计执行不变因子的微指令的个数来执行算法分析，而不必再苦恼于在特定语言或者特定硬件下分析执行在计算机上的操作的精准个数。

作为一个实际的例子，我们再来回想一下 1.4.2 节中在 python 列表中寻找最大数的要求。如代码段 3-1 所示，在介绍循环时，第一次引入了这个例子来表示一个找列表中最大值的函数。

def find_max(data):
  """Return the maximum element from a nonempty python list."""
  biggest = data[0]               # The initial value to beat
  for val in data:                # For each value:
    if val > biggest              # if it is greater than the best so far,
      biggest = val               # we have found a new best (so far)
  return biggest                  # When loop ends, biggest is the max

这是运行时间按比例增长到 n 这种算法的一个经典例子，当循环中的每一个数据元素执行一次时，一些相应数量的微指令也在这个过程中执行了一次。在本节的末尾，我们提供了一个框架来规范这个声明。

3.3.1 大 O 符号¶

令 $f(n)$ 和 $g(n)$ 作为正实数映射正整数的函数。如果有实型常量 $c> 0$ 和整型常量 $n_0\ge 1$ 满足

\[ f(n)\le cg(n)\ \ \ \ \ \ 当\ n\ge n_0 \]

我们就说 $f(n)$ 是 $O(g(n))$

这种定义就是通常说的大 O 符号，因为它有时被说成 “ $f(n)$ 是 $g(n)$ 的大 O ” 。图 3-5 展示了一般的定义。

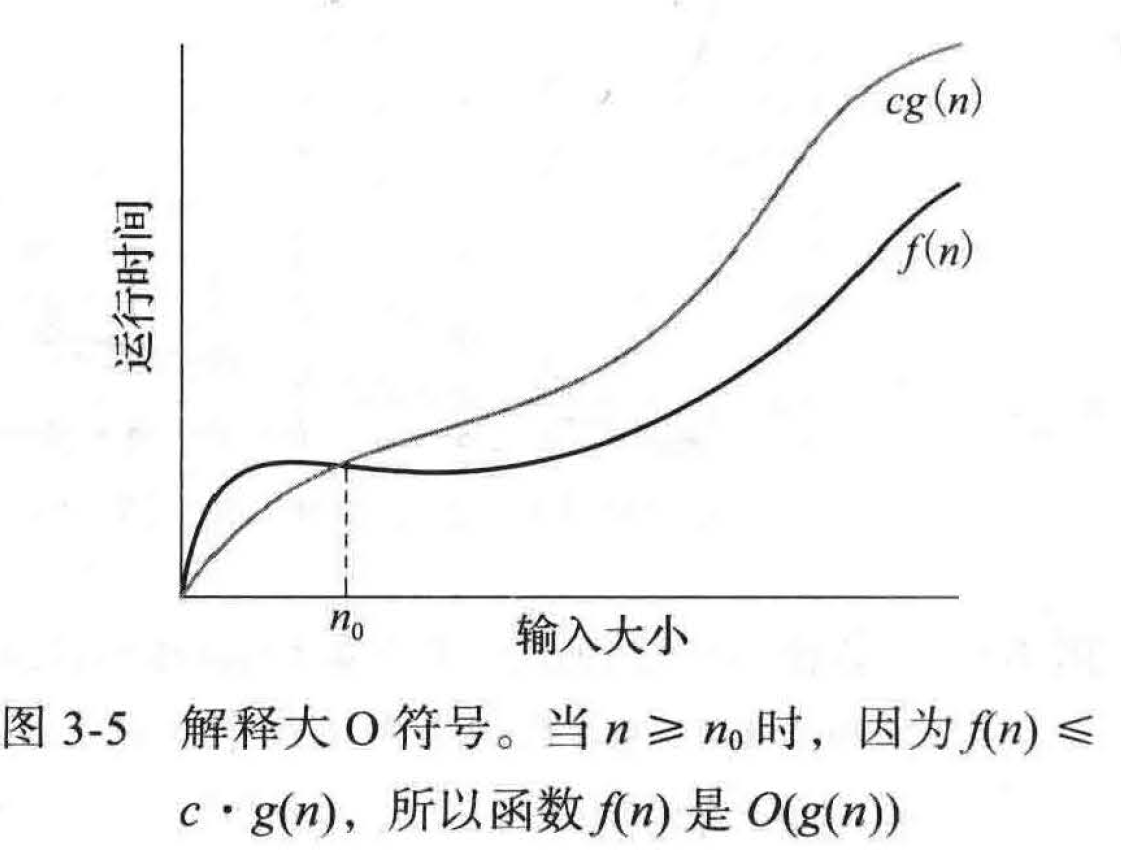
例题 3 - 6: 函数 $8n + 5$ 是 $O(n)$

证明：通过大 O 的定义，我们需要找到一个实型常量 $c > 0$ 和一个整型常量 $n_0\ge 1$, 对于任意一个整数 $n \ge n_0$。，满足 $8n + 5 ~ \le cn$ 。很容易找到一个可能的选择： $c = 9 , n_0= 5$ 。当然，这是无限种可选择组合中的一个，因为在 $c$ 和 $n_0$ 之间有一个权衡。比如说，我们能够设定常数 $c = 13, n_0= 1$ 。

大 $O$ 符号的含义是： 当给定一个常数因子且在渐近意义上 $n$ 趋于无穷时，函数 $f(n)$ “ 小于或等于＂函数 $g(n)$ 。这种思想来源于这样一个事实：从渐近的角度来说，当 $n \ge n_0$ 时，规定用 “ $\le$ ”来比较 $f(n)$ 和 $g(n)$ 与一个常数的乘积。然而，如果说 “$f(n) \le O(g(n))$" 未免显得不合适，因为大 O 已经有“ 小于或等于＂的意思。同样，如果用 “ = “ 关系的一般理解来说， “$f(n) \le O(g(n))$" 也不完全正确，尽管这很常见，因为没办法说明白 “$O(g(n)) = f(n)$" 这种对称语句。最好是说 $f(n)$ 是 $O(g(n))$

或者，我们可以说 “ $f(n)$ 是 $g(n)$ 的量级” 。如果用更倾向于数学的语言，这样说也是正确的：“$f(n)\in O(g(n))$”，从技术上说，大 O 符号代表多个函数的集合。在本书中，我们仍将大 O 声明为 "f(n) 是 O(g(n)）” 。即使这样解释，我们在如何使用大 O 符号参与算术运算上仍有相当大的自由，以及由这种自由所带来的一定的责任。

使用大 O 符号描述运行时间¶

通过设定一些参数 n, 大 O 符号被广泛用于描述运行时间和空间界限，虽然参数的设定依据问题的不同而有所不同，但（大 O 符号）仍是一种测量问题 ” 尺寸＂的可选择的方法。例如，假如我们对在一个序列中找最大数感兴趣，当使用找最大数算法时，我们应该用 n 表示这个集合中元素的个数。运用大 O 符号，我们能够为任意一台计算机写出关于找最大数算法（代码段 3-1 ) 的运行时间的数学化的精准语句。

命题 3 - 7: 找最大数算法（即计算一系列数中的最大数）的运行时间为 $O(n)$ 。

证明：在循环开始之前初始化时，仅仅需要固定数量的基本操作。循环的每一次重复也仅仅需要固定的基本操作，并且循环执行 $n$ 次。因此，我们可以通过选择适当的常数 c' 和 c “ （这两个常数在初始化和循环体中能分别反应执行状况），就可计算出基本操作的数量，即 c'+ c’’ 。因为每一个基本操作的运行时间是固定的，我们可以通过输入一个 n 值来计算找最大数算法的运行时间， 运行时间最多也就是一个常数乘以 n 。所以，我们得出结论，找最大数算法的运行时间为 O(n) 。

大 O 符号的一些性质¶

大 O 符号使得我们忽视常量因子和低阶项，转而关注函数中影响增长的主要成分。

例题 3 - 8: $5n^4 + 3n^3 + 2n^2 + 4n + 1$ 是 $O(n^4)$

证明：注意， $5n^4 + 3n^3 + 2n^2 + 4n + 1\le(5+3+2+4+1)n^4=cn^4$, 令 $c = 15$ ，当 $n\ge n_0＝ 1$ 时即满足题意

事实上，我们可以描述任何多项式函数的增长速率。

命题 3 - 9: 如果 $f(n)$ 是一个指数为 $d$ 的多项式，即

\[ f(n) = a_0+ a_1n + ···+a_dn^d \]

且 $a^d > 0$, 则 $f(n)$ 是 $O(n^d)$。

留给读者自证不难

因此，多项式中的最高阶项决定了该多项式的渐近增长速率。在练习中，我们考虑大 O 符号另外一些性质。接下来让我们来进一步考虑一些例子，这些例子主要集中在用于算法设计中的 7 个基本函数的结合上。我们依据当 $n \ge 1$ 时， $\log n \le n$ 这样的一个数学定理。

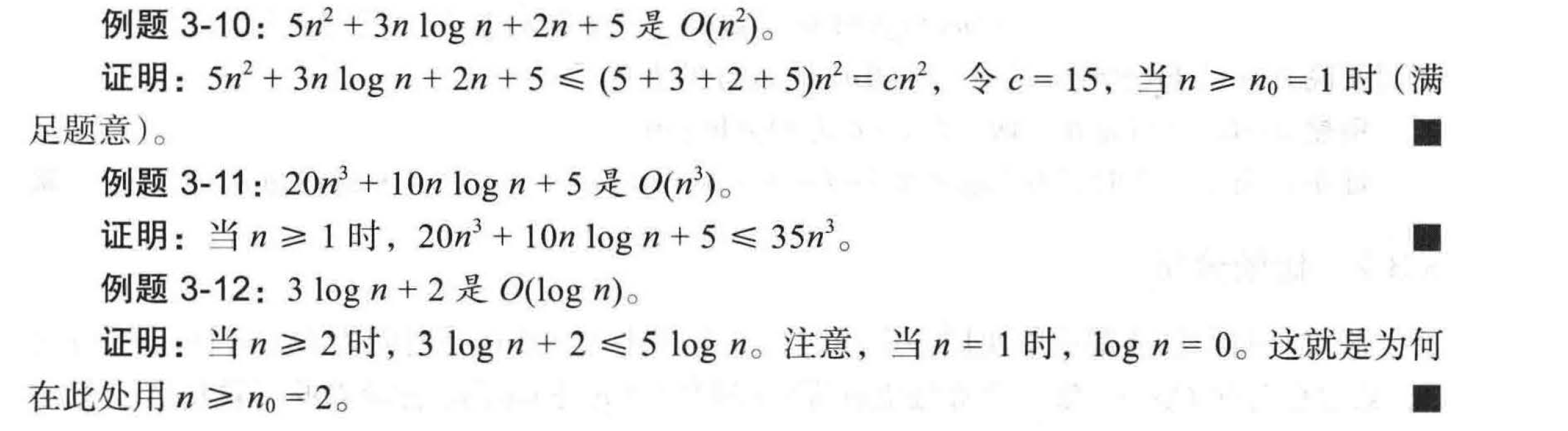
用最简单的术语描述函数¶

总的来说，我们应该用大 O 符号尽可能接近地描述函数。虽然函数 $f(n) = 4n^3 + 3n^2$ 是 $O(n^5)$ 或者甚至是 $O(n^4)$ ，但说 $f(n)$ 是$O(n^3)$ 更精确。通过类比考虑一个场景：

一位饥饿的旅行者在一条漫长的乡村小路开车，突然遇到一位刚从集市回家的农民。假设旅行者问农民自己还要开多久才能找到食物，虽然农民回答“当然不会再超过 12 个小时“也是对的，但告诉旅行者”沿着这条路再行驶几分钟就会看到一个超市”却更精确（且更有用）。因此，即便是使用大 O 符号，我们仍然需要尽可能地还原整个真相。

如果在大 O 符号里使用常数因子和低阶项，也会被认为不得体。例如，函数 $2n^2$ 是 $O(4n^2+ 6n \log n)$ ，尽管说法完全正确，但却不常用。我们应尽力用最简单的术语来描述函数。3.2 节列举的 7 个函数最常和大 O 符号结合起来描述算法的运行时间和空间使用情况。事实上，我们通常用函数的名称来引用其所描述的算法的运行时间。因此，例如，我们可以说以 $O(n^2)$ 运行的二次算法的最坏运行时间为 $4n^2 + n \log n$ 。同样，若一个算法运行时间最大为 $5n + 20 \log n + 4$ , 则这样的算法被称为线性算法。

大 Ω¶

正如大 O 提供了一种渐近说法：一个函数的增长速率“小于或等于”另一个函数，接下来的符号提供了另一种渐近说法：一个函数的增长速率”大于或等于“另一个函数。

设 $f(n)$ 和 $g(n)$ 为正实数映射正整数的函数，如果 $g(n)$ 是 $O(f(n))$，即存在实常数 $c > 0$ 和整型常数 $n_0\ge1$ 满足

\[ f(n)\ge cg(n)\ \ \ \ \ \ 当\ n\ge n_0 \]

我们就说 $f(n)$ 是 $ \Omega(g(n))$，表述为 "$f(n)$ 是 $g(n)$ 的大 $\Omega$” 。这个定义允许我们采用渐近的说法：当给定一个常数因子时，一个函数大于或等于另一个函数

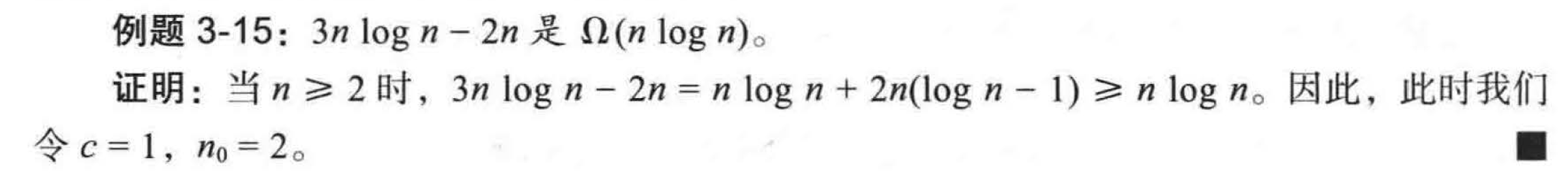
大 Θ¶

此外，有一个符号允许我们说： 当给定一个常数因子时，两个函数的增长速率相同。如果 $f(n)$ 是 $O(g(n))$，且 $f(n)$ 是 $\Omega(g(n))$，即存在实常数 $c'> 0 、c'' > 0$ 和一个整型常数 $n_0\ge1$ 满足

\[ c'g(n)\le f(n)\le c''g(n),\ \ \ 当\ n\ge n_0 \ 时 \]

我们就说 $f(n)$ 是 $\Theta(g(n))$，描述为 “$f(n)$ 是 $g(n)$ 的大 $\Theta$” 。

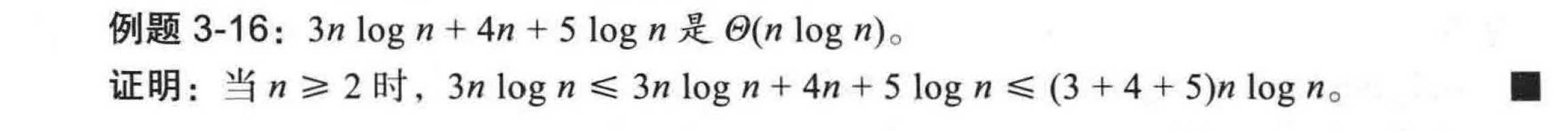
3.3.2 比较分析¶

假设有两个算法都能解决同一个问题：一个算法 A, 其运行时间为 O(n) ；另一个算法 B , 其运行时间 O(n^2) 哪一个算法更好呢？我们知道 n 是 $O(n^2)$ ，这就意味着算法 A 比算法 B 更具有渐近性，虽然当 n 的值较小时，算法 B 的运行时间可能低于 A

我们使用大 O 符号依据渐近增长率来为函数排序。在下面的序列中，我们将 7 个函数按升序排序，即，假如函数 $f(n)$ 在函数 $g(n)$ 之前，那么 $f(n)$ 就是 $O(g(n)) : 1 , \log n , n, n \log n, n^ 2, n^3, 2^n$

在表 3 -3 中，我们进一步举例说明渐近观点的重要性。该表探讨了允许一个输入实例的最大值，该实例由某个算法分别运行在 1 秒、1 分钟和 1 小时的时候产生。该表显示了一个好的算法设计的重要性： 缓慢渐近算法由于运行时间长从而被快速渐近算法所击败，尽管常数因子对于快速渐近算法而言可能更糟。

然而，好的算法设计的重要性不仅仅是在一台给定的计算机上高效地解决问题。如表 3 -4 所示，即使硬件更新速度飞快，我们仍不能克服一个缓慢渐近算法的弊端。假设给定运行时间的算法运行在比以往计算机快 256 倍的计算机上，该表给出了在任意的常量时间所能解决的最大问题量。

一些注意事项¶

这里就渐近符号做一些提醒。首先，注意大 O 符号和其他符号在使用时可能会被误导，因为它们“ 隐藏 ”的常数因子可能非常大。例如，虽然函数 $10^ {100}n$ 是 $O(n)$，但与运行时间为 $10n \log n$ 的算法相比，虽然线性算法渐近速度更快，我们可能更倾向于选择运行时间为 $O(n \log n)$ 的算法。之所以这样，是因为常数 $10^{100}$ 被称为“天文数字”，在观测宇宙时，许多天文学家一致认为该数字是原子数目的上限。所以，我们不可能得到一个像输入大小一样大的现实问题，因此，在使用大 O 符号时，我们应该注意被“隐藏”的常数因子和低阶项。

上述观测引发了这样的问题：什么是“快速＂算法。一般来说，任何算法的运行时间为 $O(n \log n)$ （在给定一个合理的常数因子的情况下），都应被认为是高效的，甚至运行时间为 $O(n^2)$ 的算法在一些情形下，比如 n 很小时，也被认为是快速的。但如果算法的运行时间为 $O(2^n)$ ，则大多数情况不会被认为是高效的。

指数运行时间¶

有一个著名的关于国际象棋发明者的故事。他要求国王在象棋的第一个格只需支付 1 粒米，第二格 2 粒，第三格 4 粒，第四格 8 粒，以此类推。如果使用编程技巧编写一个程序来精确计算国王应支付的米粒数量，这将会是一个有趣的测试。

如果必须在高效和不高效算法之间划清界限，那么很自然，多项式运行时间和指数运行时间将会是一个明显的区别。也就是说，区分运行时间 $O(n^c)$ 是否为快速算法，只需看常数 $c$ 是否满足 $c > 1$; 区分运行时间 $O(b^n)$ 是否为快速算法，只需看常数 $b$ 是否满足 $b>1$ 。本节讨论的许多概念也应该看作 “ 盐粒＂，因为运行时间为 $O(n^{100})$ 的算法可能不被认为是 “ 高效 ” 的。即便如此，多项式运行时间和指数运行时间的区别仍被认为是健壮易处理的方式。

3.3.3 算法分析示例¶

既然我们用大 O 符号能进行算法分析，接下来给出使用该符号来描述一些简单算法的运行时间的若干示例。此外，为了和之前的约定保持一致，我们将介绍本章给出的 7 个函数是如何被用于描述算法实例的运行时间的。

在本节中，我们不再使用伪代码，而是给出完整的能够实现的 python 代码。我们用 python 的 list 类自然地表示数组的值。在第 5 章，我们将深入研究 python 的 list 类以及该类所提供的各种方法的效率。在本节中，我们仅仅介绍几种方法来讨论它们的效率。

常量时间操作¶

给出一个 python 的 list 类的实例，将其命名为 data, 调用函数 len(data) ，在固定的时间内对其进行评估。这是一个非常简单的算法，因为对于每一个列表， list 类包含一个能记录列表当前长度的实例变量。这就使得该算法能立即得出列表的长度，而不用再花时间迭代计算列表中的每个元素。使用渐近符号，我们说函数的运行时间为 O(1) ，也就是说．函数的运行时间是独立于列表长度 n 的。

python 的 list 类的另一个重要特征是能使用整数索引 $j$ 写出 data[j] 来访问列表中的任意元素。因为 python 列表是基于数组序列执行的，列表中的元素存储在连续的内存块内。之所以能搜索到列表中的第 j 个元素，不是靠迭代列表中的元素得到的，而是通过验证索引， 并把该索引作为底层数组的偏移址得到的。反过来，对于某一元素，计算机硬件支持基于内存地址的常量时间访问。因此，我们说 python 列表的 data[j] 元素的运行时间被估计为 O(1) 。

回顾在序列中找最大数的问题¶

在开始下一个示例之前，我们先来回顾一下代码段 3-1 中的 find_max 算法，即在列表中找最大值。在命题 3 -7 中，我们得出该算法的运行时间为 O(n) 。这符合我们之前的分析：语法 data[0] 的初始化运行时间为 O(1) 。该循环执行 n 次，在每次循环中，都执行一次比较，可能也会执行一次赋值语句（以及维持循环变量）。最后，我们注意到 python 返回语句机制运行时间也为 O(1) 。综上所述，我们得出算法 find_max 的运行时间为 O(n) 。

进一步分析找最大值算法¶

关于 findmax 算法，有一个更有趣的问题：我们要更新多少次当前 “ 最大＂值？ *在最坏的情况下，即给出的顺序按升序排列，最大值将会被重新赋值 n - 1 次。但如果给出的是随机序列．即任何情况都可能出现，在这种情况下，如何预测最大值将会被更新多少次**？要回答这个问题，应注意在循环的每一次迭代中，只有当前元素比以往所有元素都更大时才会更新当前最大值。如果给出的是随机序列，则第 $j$ 个元素比前 $j$ 个元素更大的概率是 $1 /j$ （假定元素唯一）。因此，我们更新最大值（包括初始化）的预期次数是 $H_n=\sum*{j=1}^n\frac1j$ ), 这就是著名的 n 调和数。

这（见附录中的命题 B-16) 表明 $H_n$ 的运行时间是 O(log n) 。因此，在 find_max 算法中， 基于随机序列，该算法的最大值被更新的预期次数是 O(log n) 。

前缀平均值¶

我们要讨论的下一个问题是著名的计算一个序列的前缀平均值。换句话说，给出一个包含 $n$ 个数的序列 $S$, 我们想计算出序列 A, 该序列满足的条件为：当 $j＝ 0, ···, n - 1$ 时， $A[j]$ 是 $S[0], ·· ·, S[j]$ 的平均值，即

\[ A[j]=\frac{\sum_{i=0}^jS[i]}{j+1} \]

在经济学和统计学中，有很多计算前缀平均值的方法。比如，给出一个公共资金的每年收益，并把这些收益从过去到现在依次排列，投资者往往关注最近一年、三年或五年等的年平均收益。同样，给出一连串的日常网络使用日志，网站管理者可能希望能追踪不同时期的平均使用趋势。我们将分析三种能用于解决这些问题的方法，且该三种方法的运行时间截然不同。

二次－时间算法

为了计算前缀平均值，我们给出第一个算法（如代码段 3 -2 所示），并将其命名为 prefix_average1 。该算法使用内部循环计算部分和，因而能独立计算出序列 A 的每一个元素。

def prefix_average1(S):
  """Return list such that, for all j, A[j] equals average of S[0], ..., S[j]."""
  n = len(S)
  A = [0] * n                     # create new list of n zeros
  for j in range(n):
    total = 0                     # begin computing S[0] + ... + S[j]
    for i in range(j + 1):
      total += S[i]
    A[j] = total / (j+1)          # record the average
  return A

为了分析算法 prefix_average1, 我们对每步执行情况进行讨论。

在本节开始处已给出 n = len(S) ，且执行时间固定。
语句 A = [0] * n 用于创建和初始化 python 列表，列表长度为 n, 每个元素值为 0 。因每个元素都执行相同次数的原子操作，故该算法的运行时间为 O(n) 。
for 循环有两层嵌套，分别由计数器 j 和 i 独自约束。外层循环被计数器 j 约束，j 从 0 增长到 n - 1, 共执行 n 次。因此，语句 total = 0 和 A[j] = total/(j + 1) 各被执行 n 次。这表明这两条语句加上 j 在此范围的执行，使得原子操作的次数按比例增长到 n , 即其运行时间为 O(n) 。
内层循环被计数器 i 约束，执行 j + 1 次，具体执行次数取决于外层循环 j 的值。因此，内层循环中的语句 total += S[i] 共执行 1+2+3 + … + n 次。通过回顾命题 3-3，我们知道 1 + 2 + 3+ … + n = n(n + 1)/2, 这就表明内层循环的语句使得该算法运行时间变为 $O(n^2)$。对于和计数器 i 相关的原子操作，也可以做类似的论证，其运行时间也为 $O(n^2)$。

将上述三项运行时间相加，即可得出执行算法 prefix_average1 的执行时间。第一项和第二项的运行时间为 O(n) ，第三项的运行时间为 $O(n^2)$。通过简单运用命题 3 -9, 得出算法 prefix_ average1 的运行时间为 $O(n^2)$

接下来介绍第二种计算前缀平均值的算法 prefix_average2 , 如代码段 3-3 所示

def prefix_average2(S):
  """Return list such that, for all j, A[j] equals average of S[0], ..., S[j]."""
  n = len(S)
  A = [0] * n                     # create new list of n zeros
  for j in range(n):
    A[j] = sum(S[0:j+1]) / (j+1)  # record the average
  return A

该方法本质上和算法 prefix_average1 一样，都属于高级算法，只是不再使用内层循环，转而使用单一表达式 sum(S[O : j + 1]) 来计算部分和 S[0] +… +S[j] 。利用 sum 函数极大地简化了算法的规模，但是否对效率有影响值得思考。从渐近的角度来说，没有比该算法更好的了。虽然表达式 sum(S[O: j + 1])看起来似乎是一条指令，但它却是一个函数调用，并能评估出该函数在算法中的运行时间为 O(j ＋ 1) 。从技术上讲，这一句计算 S[O: j + 1] 运行时间也为 O(j + 1) ，因为它构造了一个新的实例存储列表。因此算法prefix_average2 的运行时间仍被一系列步骤所决定，这些步骤按比例运行时间为 1+2+3+ …＋ n, 因此仍为 $O(n^2)$

线性时间算法

接下来给出最后一个算法 prefix_average3, 如代码段 3-4 所示。就像前两个算法一样，我们热衷于对每个 j 计算前缀和 $S[0] + S[1] + … ＋ S[j]$ ，并在代码中以 total 表示，以便能够进一步计算前缀平均值 A[j] ＝ total/(j + 1)。不过，与前两个算法不同的是该算法更高效。

def prefix_average3(S):
  """Return list such that, for all j, A[j] equals average of S[0], ..., S[j]."""
  n = len(S)
  A = [0] * n                   # create new list of n zeros
  total = 0                     # compute prefix sum as S[0] + S[1] + ...
  for j in range(n):
    total += S[j]               # update prefix sum to include S[j]
    A[j] = total / (j+1)        # compute average based on current sum
  return A

在前两个算法中，对每一个 j, 都要对前缀和重新进行计算。因每一个 j 都需要 O( j ) 的运行时间，从而导致该算法运行时间变为二次。在算法 prefix_average3 中，我们动态保存当前的前缀和，用 total + S[j] 高效计算 $S[0] + S[1] + … ＋ S[j]$ ，这里 total 的值就等于先前算法循环执行到 j 时的和 $S[0] + S[1] + … ＋ S[j-1]$ 。对算法 prefix_average3 运行时间的分析如下：

初始化变量 n 和 total, 用时 O(1) 。
初始化列表 A, 用时 O(n) 。
只有一个 for 循环，用计数器 j 来约束。计数器在循环范围内持续迭代，使得 total 用时 O(n) 。
j 从 0 到 n - 1 ，循环体被执行 n 次。因此，语句 total += S[j] 和 A[j] = total/(j + 1) 各被执行 n 次。因为这两条语句每次迭代用时 O(1) ，所以共用时 O(n) 。

通过对上述四项求和便可得出算法 prefix_a verage3 的运行时间。第一项是 O(1) ，剩余三项是 O(n) 。通过对命题 3-9 的简单运用，得出 prefix_average3 的运行时间为 O(n) ，比二次算法 prefix_average 1 和 prefix_average2 运行效率更高。

三集不相交¶

假设我们给出三个序列 A 、B 、C 。假定任一序列没有重复值，但不同序列间可以重复。三集不相交问题就是确定三个序列的交集是否为空，即不存在元素 x 满足 $x\in A 、x\in B$ 且 $x\in C$。代码段 3-5 给出了一个简单的 python 函数来确定这个性质

def disjoint1(A, B, C):
  """Return True if there is no element common to all three lists."""
  for a in A:
    for b in B:
      for c in C:
        if a == b == c:
          return False      # we found a common value
  return True               # if we reach this, sets are disjoint

这个简单的算法将遍历三个序列任一组可能的三个值并且确定这些值是否相等。假如最初序列每一个长度都为 n, 在最坏情况下，该函数的运行时间为 $O(n^3)$

我们可以用一个简单的观测来提高渐近性。一旦在循环 B 中发现此时的元素 a 和 b 不相等，再去遍历 c 为了找三个相等的数，则就浪费时间了。在代码段 3-6 中，利用观测思想，给出了解决该问题的改进方案。

def disjoint2(A, B, C):
  """Return True if there is no element common to all three lists."""
  for a in A:
    for b in B:
      if a == b:            # only check C if we found match from A and B
        for c in C:
          if a == c         # (and thus a == b == c)
            return False    # we found a common value
  return True               # if we reach this, sets are disjoint

在改进方案中，如果运气好，则不仅能节省时间。对于 disjoint2, 我们声明在最坏情况下的运行时间为 $O(n^2)$。这里要考虑许多二次对(a, b) 。假如 A 和 B 均为没有重复值的序列，最多会有 $O(n)$ 。因此，最内层的循环 C 最多执行 n 次。

为了计算总的运行时间，我们检测每一行代码的执行时间。for 循环在 A 上需要运行 O(n) ，在 B 上共需要 $O(n^2)$ ，因为该循环被执行在 n 个不同的时间段。预计语句 a == b 的运行时间为 $O(n^2)$ 。剩下的运行时间取决于找到多少匹配的 (a, b) 对。因为我们已经注意到，最多有 n 对，因此 for 循环在 C 上以及循环体内的执行最多用时 $O(n^2)$。通过规范运用命题 3 - 9 , 得出总的运行时间为 $O(n^2)$

元素唯一性¶

与三集不相交紧密相关的便是元素唯一性问题。前面我们给出三个集合并假定任一集合内元素不重复。在元素唯一性问题中，我们给出一个有 $n$ 个元素的序列 $S$ , 求该集合内的所有元素是否都彼此不同。

def unique1(S):
  """Return True if there are no duplicate elements in sequence S."""
  for j in range(len(S)):
    for k in range(j+1, len(S)):
      if S[j] == S[k]:
        return False              # found duplicate pair
  return True                     # if we reach this, elements were unique

我们对此问题的第一个解决方案便是采用一个简单的迭代算法。在代码段 3 -7 中给出函数 unique1 ，用于解决元素唯一性问题。该函数通过遍历所有下标 $j<k$ 的不同组合，检查是否有任一组合两元素相等。该算法使用两层循环，外层循环的第一次迭代致使内层循环 n- 1 次迭代，外层循环的第二次迭代致使内层循环 n -2 次，以此类推。因此，在最坏情况下，该函数的运行时间按比例增长到

\[ (n - 1) + (n - 2) +… +2 + 1 \]

通过命题 3 -3 , 我们得出总运行时间仍为 $O(n^3)$

以排序作为解决问题的工具

解决元素唯一性问题更优的一个算法是以排序作为解决问题的工具。在此情况下，通过对序列的元素进行排序，我们确定任何相同元素将会被排在一起。因此，为了确定是否有重复值，我们所要做的就是遍历该排序的序列，查看是否有连续的重复值。该算法的一个 python 实现方法如代码段 3 -8 所示：

def unique2(S):
  """Return True if there are no duplicate elements in sequence S."""
  temp = sorted(S)                # create a sorted copython of S
  for j in range(1, len(temp)):
    if S[j-1] == S[j]:
      return False                # found duplicate pair
  return True                     # if we reach this, elements were unique

如 1.5.2 节所述，内置函数 sorted 的基本功能是对原始列表的元素进行一次有序排序后产生的一个新列表。该函数保证在最坏情况下其运行时间为 $O(n \log n)$ ；详见第 12 章对常见排序算法的讨论。一旦数据被排序，下面的循环运行时间就变为 O(n) ，因此算法 unique2 的总运行时间为 $O(n \log n)$

3.4 简单的证明技术¶

有时，我们会想做关于一个算法的声明，如显示它是正确的或者它的运行速度很快。为了使声明更加严谨，我们必须使用数学语言。为了证实这样的说法，我们必须对声明加以证明。幸运的是，有几种简单的方法可以做到这一点。

3.4.1 示例¶

有些声明的一般形式为：“在集合 S 中，存在具有性质 P 的元素 x” 。为了证明这个说法，我们只需要生成一个特定的元素 x, 它在集合 S 中并具有性质 p 。同样，一些难以置信的声明的一般形式为： “在集合 S 中，任一元素 x 都具有性质 P” 。为了证明这种声明是错误的，我们只需生成一个特定的元素 x, 它在集合 S 中并不具有性质 P 。这样的实例就是一个反例。

3.4.2 反证法¶

另一种证明技术涉及否定的使用。两个主要的这类方法是逆否命题和矛盾的使用。逆否命题方法的使用就像透过镜子的反面进行观察。为了证明命题“如果 p 为真，那么 q 为真”，我们使用命题 “ 如果 q 非真，那么 p 非真”来代替。从逻辑上讲，这两个命题是相同的，但是后者，就是第一个命题的逆否命题，可能更容易思考。

矛盾

另一个反证方法是通过矛盾来证明，这也常常涉及德摩根定律的使用。通过矛盾的方法进行证明时，我们建立一个声明 q 是真的，首先假设 q 是假的，然后显示出由这个假设导致的矛盾（如 $2 \neq 2$ 或 $1 > 3$) 。通过这样的一个矛盾，我们可以得出如果 q 是假的，那么没有一致的情况存在，所以 q 必须是真的。当然，为了得出这个结论，在假设 q 是假的之前，必须确保我们的情况是一致的。

例题 3-19: 设 a 和 b 都是整数，如果 ab 是奇数，那么 a 是奇数并且 b 也是奇数

证明：设 ab 是奇数。我们希望得到 a 是奇数并且 b 也是奇数。所以，希望出现与假设相反的矛盾，即假设 a 是偶数或者 b 是偶数。事实上，为了不失一般性，我们甚至可以假设 a 是偶数的情况（因为 b 的情况是对称的）。然后我们设 $a= 2j$ , 其中 j 是整数。因此， $ab=(2j)$， $b = 2 (jb)$ ，得出 ab 是偶数。但这是一个矛盾： ab 不能既是奇数又是偶数。因此， a 是奇数并且 b 也是奇数

3.4.3 归纳和循环不变量¶

我们所做出的关于运行时间或空间约束的大多数声明都包括一个整数参数 n （通常表示该问题的“大小＂的直观概念） 。此外，大多数的这些声明相当于 “ 对于所有 $n \ge 1, q(n)$为真”这样的语句。由于这是一个关于无限组数字的声明，我们不能以直接的方式穷尽证明这一点。

归纳

但是，通过使用归纳的方法，我们通常可以证明上述声明是正确的。这种方法表明，对于任何特定的 $n \ge 1$, 有一个有限序列的证明，从已知为真的东西开始，最终得出 q(n) 为真的结论。具体地说，通过证明当 n = 1 时， q(n) 为真，我们开始用归纳法证明（可能还有其他一些值 $n = 2, 3, …,k, k$ 为一个常数）。然后，我们证明当 n > k 时归纳＂步骤 ” 为真，即表明”对于所有 j < n, 如果 q(j) 为真，那么 q(n) 为真。”将这两块部分合起来即可完成归纳的证明。

对于所有 $n\ge1$ 的情况，我们有时会感到证明一些事情为真的任务让我们不堪重负。但是，我们应该记住归纳法的具体步骤。这表明，对于任何特定的 n, 通过一系列的有限、逐步的证明，从已知为真的东西开始，最终得出关于 n 的真实性。总之，归纳论证为一系列直接证明提供了模板。

循环不变量¶

在本节中，我们最后讨论的证明方法是循环不变量。为了证明一些关于循环的语句 $L$ 是正确的，我们依据一系列较小的语句 $L_0, L_1 , · · · , L_k$ 来定义 $L$ , 其中：

在循环开始前，最初要求 $L_0$ 是真的
如果在迭代 j 之前 $L_{j-1}$ 为真，那么在迭代 j 之后 $L_j$ 也会为真。
最后的语句 $L_k$ 意味着想要证明的语句 L 为真

让我们以一个简单的用到循环不变量参数的例子来证明算法的正确性。尤其是，用一个循环不变量来证明函数 find （参见代码段 3 -9 ),

找出出现在序列 S 中元素 val 的最小索引值

def find(S, val):
  """Return index j such that S[j] == val, or -1 if no such element."""
  n = len(S)
  j = 0
  while j < n:
    if S[j] == val:
      return j          # a match was found at index j
    j += 1
  return -1

为了说明 find 函数为真，我们归纳定义一系列的语句 $L_j$ , 来推断算法的正确性。具体地说，在 while 循环迭代 j 的开始，我们认为以下的叙述为真：

$L_j$： val 不等于序列 S 中的第一个元素 j 的任何一个

循环的第一次迭代开始时，这种声明为真，因为 j 是 0 , 序列 S 中的第一个 0 中没有元素（这样的一个非常真实的声明被称为空存）。在第 j 次迭代中，我们比较元素 val 和元素 S[j] ，如果这两种元素是相等的，那么返回索引值 j , 在这种情况下，这显然是正确的并且可以完成这个算法。如果两个元素 val 和 S[j] 是不相等的，那么我们可以多一个不等于 val 的元素，并把索引值 j 加一。因此，对于这个新的索引值 j , 这个声明 $L_j$ 会变成真，于是在下一次迭代开始时它为真。如果 while 循环终止而没有返回序列 S 中的任何一个索引值，则有 j = n 。也就是说， $L_n$ 为真——在序列 S 中没有与 val 相等的元素。因此，该算法准确的返回 - 1，以指示在序列 S 中没有元素 val 。

对于渐进分析的一些注解¶

在评价算法运行效率时，我们往往可以忽略其处理小规模问题时的能力差异，转而关注其在处理更大规模问题时的表现。其中的原因不难理解，小规模问题所需的处理时间本来就相对更少，故此时不同算法的实际效率差异并不明显；而在处理更大规模的问题时，效率的些许差异都将对实际执行效果产生巨大的影响。这种着眼长远、更为注重时间复杂度的总体变化趋势和增长速度的策略与方法，即所谓的渐进分析（asymptotic analysis）

这段话不难理解，简单来说就是，渐进分析关注的是算法执行效率随问题规模增长的变化趋势和增长速度。如果绘制成函数曲线，我们就是要看这条曲线“陡不陡”。

如果将执行效率拆分开来，算法的复杂度又可以分为渐进时间复杂度和渐进空间复杂度。

渐进时间复杂度分析中，可以粗略的认为每行代码的执行时间是一致的，从而对代码执行次数进行分析。如果借助了编程语言的工具库，还需要考虑这部分的时间成本。

渐进空间复杂度分析中，原始输入的数据不计入到空间占用中，只有在算法中创建的才会计入

大 O 记号¶

大 O 记号为了刻画变化趋势和增长速度，可以忽略掉常数项和低次项：

在大 O 记号的意义下，函数各项正的常系数可以忽略并等同于 1。多项式中的低次项均可忽略，只需保留最高次项。可以看出，大 O 记号的这些性质的确体现了对函数总体渐进增长趋势的关注和刻画。

我们不难看出，大 O 记号使用最高次项表示算法的复杂度，是一种对算法复杂度最坏情况的估算。

大 Ω 记号和大 Θ 记号¶

这里的称作“大 Ω 记号”（big-Ω notation）。与大 O 记号恰好相反，大 Ω 记号是对算法执行效率的乐观估计。

也就是说，大 Ω 记号是用来表示算法执行的最好情况的。

大 Ω 记号和大 O 记号确定了算法复杂度的上下边界，那么有没有准确估计算法复杂度的记号呢？当然是有的，这种准确估计算法复杂度的表示方法称为大 θ 记号。

计算渐进时间复杂度¶

在我们了解了复杂度分析的概念和表示方法后，我们尝试着去计算几种常见的时间复杂度。

常数复杂度¶

常数复杂度是所有算法的终极梦想，因为这种复杂度代表着无论问题规模多大，都能在明确的时间内执行完成。

随便搞一段代码：
public int add(int a, int b) {
int sum = a + b;
return sum;
}
这段代码中，无论 a 和 b 输入什么，都只会执行 3 行代码，这种不随着输入规模而改变执行时间的就是常数级复杂度。

大 O 记号中表示为： $O(1)$ 。无论执行几行，只要是能够确定的，都表示为 $O(1)$ 。

线性复杂度¶

再搞一段代码：
public void add(int n) {
int result = 0;
for (int i = 0; i < n; i++) {
result ++;
}
}
不难看出，这段代码总共会执行 ($1+2n$) 行代码，那么执行时间也是 ($1+2n$) 。

根据大 O 记号中的结论，我们可以忽略掉所有的常数，得到的时间复杂度是 $O(n)$ 。

事实上， $2n$ 和 $n$ 的增长趋势是有一定差异的，但整体的变化趋势是随着 $n$ 的增大而线性增大的，因此我们依旧可以忽略掉常数项和常数系数。

第 3 章 算法分析