第 4 章 递归
在计算机程序中,描述迭代的一种方法是使用循环,比如在 1.4.2 节中描述的 python 语言的 while 循环和 for 循环。另一种完全不同的迭代实现方法就是递归。
递归是一种技术,这种技术通过一个函数在执行过程中一次或者多次调用其本身,或者通过一种数据结构在其表示中依赖于相同类型的结构更小的实例。在艺术和自然界中有很多递归的例子。例如分形图是自然方面的递归。一个在艺术中应用递归的例子是俄罗斯套娃。每个娃娃要么是实木的,要么是空心的,并且空心的娃娃里面包含了另一个俄罗斯套娃。
在计算中,递归提供了用于执行迭代任务的优雅并且强大的替代方案。事实上,一些编程语言(例如 Scheme 、Smalltalk) 不明确支持循环结构,而是直接依靠递归来表示迭代。大多数现代编程语言都通过和传统函数调用相同的机制支持函数的递归调用。当函数的一次调用需要进行递归调用时,该调用被挂起,直到递归调用完成
在数据结构和算法的研究中,递归是一种重要的技术。我们将在本书的后面几个章节中多次使用递归(尤其是第 8 章和第 12 章) 。在本章中,我们将从以下四个递归使用例证开始,并给出了每个例证的 python 实现。
- 阶乘函数(通常表示为 \(n!\) )是一个经典的数学函数,它有一个固有的递归定义
- 英式标尺具有的递归模式是分形结构的一个简单例子。
- 二分查找是最重要的计算机算法之一。在一个拥有数十亿以上条目的数据集中,它能让我们有效地定位所需的某个值。
- 计算机的文件系统有一个递归结构,在该结构中,目录能够以任意深度嵌套在其他目录上。递归算法被广泛用千探索和管理这些文件系统。
我们接下来讨论如何进行一个递归算法的运行时间的形式化分析,并且讨论在定义递归时一些潜在的缺陷。在内容的选择上,我们提供了更多的递归算法的例子,强调了一些常见的设计形式。
4.1 说明性的例子¶
4.1.1 阶乘函数¶
为了说明递归的机制,我们首先介绍一个计算阶乘函数的值的简单数学示例。一个正整数 \(n\) 的阶乘表示为 \(n!\) ,它被定义为整数从 1 到 n 的乘积。如果 \(n = 0\), 那么按照惯例 n!被定义为 1 。更正式的定义是,对于任何整数 \(n \ge 0\)
例如, 5! = 5 X 4 X 3 X 2 X 1 = 120 。阶乘函数很重要,其结果等于 n 个元素全排列的个数。例如, 三个字符 a 、b 和 c 有 3! =3 X 2 X 1 =6 种不同的排列方式: abc 、acb 、bac 、bca 、cab 和 cba 。
阶乘函数有一个固有的递归定义。通常,对于一个正整数 n, 我们可以定义 \(n! = n \times (n - 1) !\) 。这个递归定义可以形式化为
在许多递归定义中,这个定义是很典型的。首先,它包含一个或多个基本情况,根据定量,这些基本情况通常被直接定义。在这个定义中, n = 0 是一个基本情况。它还包含一个或多个递归情况,这些情况的定义服从被定义函数的定义
阶乘函数的递归实现¶
递归不仅是一个数学符号,也可以用于设计一个阶乘函数,如代码段 4-1 所示。
def factorial(n):
if n == 0:
return 1
else:
return n * factorial(n-1)
这个函数不使用任何显式循环。迭代是通过函数的重复递归调用来实现的。在这个定义中没有循环,因为函数每被调用一次,它的参数就会变小一次,当达到基本情况的时候,递归调用就会停止
我们用递归跟踪的形式来说明一个递归函数的执行过程。跟踪的每个条目代表着一个递归调用。每一个新的递归函数调用用一个向下的箭头指向新的调用来表示。函数返回时,用一个弯曲的箭头表示,并将返回值标在箭头的旁边。图 4 - 1 所示为一个对阶乘函数进行跟踪的示例。
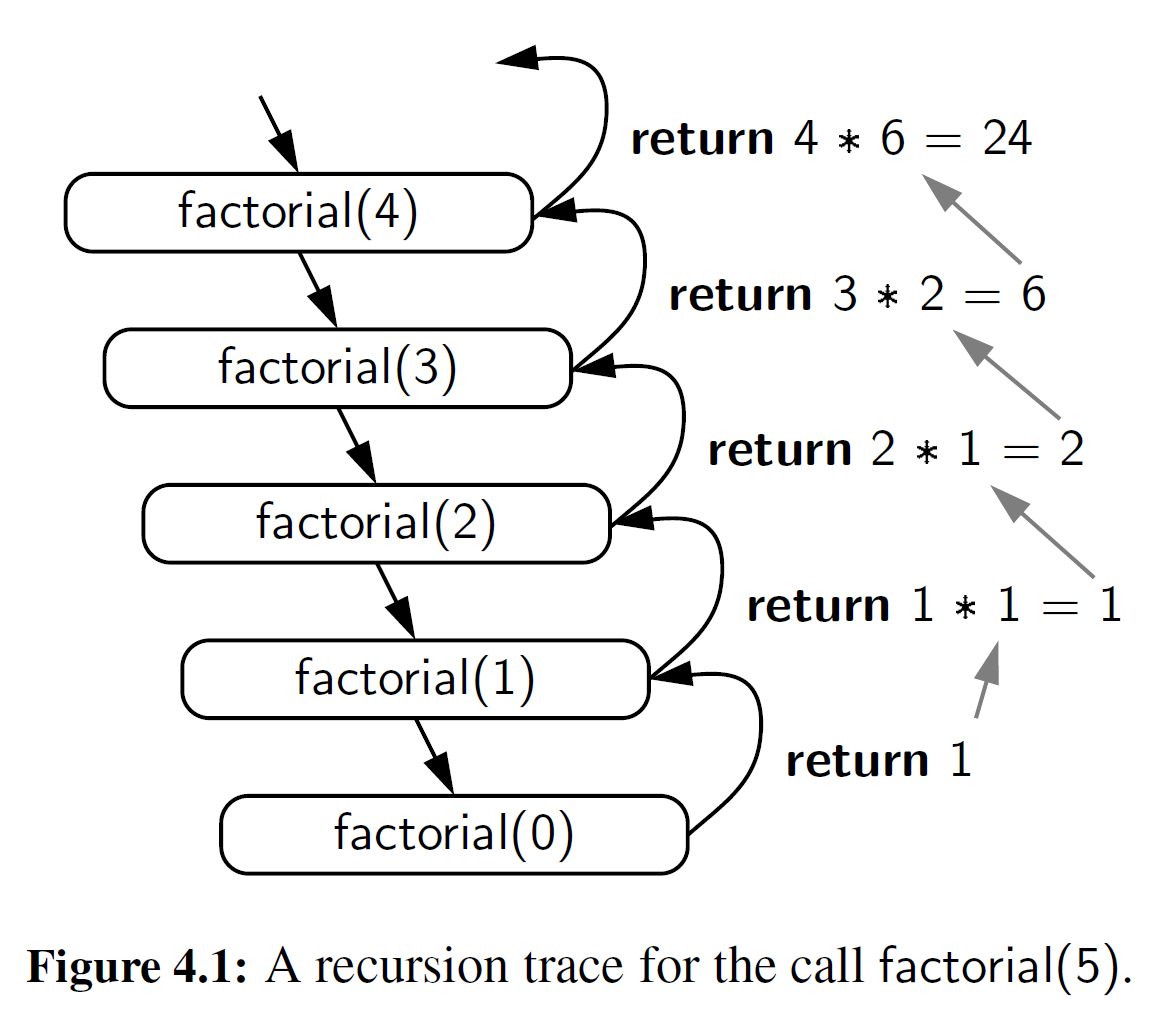
递归跟踪密切反映了编程语言对于递归的执行。在 python 中,每当一个函数(递归或其他方式)被调用时,都会创建一个被称为活动记录或框架的结构来存储信息,这些信息是关于函数调用的过程的。这个活动记录包含一个用来存储函数调用的参数和局部变量的命名空间(参见 1.1 0 节命名空间的讨论),以及关于在这个函数体中当前正在执行的命令的信息。
如果一个函数的执行导致嵌套函数的调用,那么前者调用的执行将被挂起,其活动记录将存储源代码中的位置,这个位置是被调用函数返回后将继续执行的控制流。该过程可以用在标准情况下一个函数调用另一个不同的函数,或用在一个函数调用自身的递归情况下。关键的一点是对于每个有效的调用都有一个不同的活动记录。
4.1.2 绘制英式标尺¶
在计算阶乘的情况下,也可以采用循环来实现迭代,不一定必须采用递归的方法。举一个更复杂的使用递归的例子,考虑如何绘制出一个典型的英式标尺的刻度。对于每一英寸 ( in , lin = 2.54cm) ,我们用一个数字标签做上刻度标记。我们表示刻度的长度并且指定一个英寸作为主刻度线的长度。在整个英寸刻度之间,标尺包含一系列较小的刻度线,如 1/2 英寸、1/4 英寸,等等。当间隔的大小减少了一半时,刻度线的长度也减 1 。图 4-2 展示了几个这样的具有不同主刻度长度的标尺(虽然不是按比例绘制) 。

绘制标尺的递归方法¶
英式标尺模式是分形的一个简单示例,也就是具有在各级放大的自递归结构的形状。考虑在图 4 -2 b 中所示的刻度线长度为 5 的标尺,忽略包含 0 和 1 的刻度线, 考虑如何绘制这些刻度线之间的刻度序列。中央刻度线(在 1/2 英寸处)的长度为 4 。观察中央刻度线上面和下面两个部分的刻度,发现它们是相同的,并且每部分有一个长度为 3 的中央刻度线。
一般情况下,中央刻度线长度 \(L \ge 1\) 的刻度间隔的组成如下:
- 一个中央刻度线长度为 \(L-1\) 的刻度间隔
- 一个长度为 \(L\) 的单独的刻度线
- 一个中央刻度线长度 \(L - 1\) 的刻度间隔
虽然可以使用一个迭代过程绘制这样的标尺(参见练习 P-4.25) ,但是这个任务用递归完成更加容易。如代码段 4-2 所示,代码实现包括三个函数。主函数 draw_ruler 管理整个标尺的构建。它的参数指定标尺的总长度以及主刻度线的长度。功能函数 draw_line 用指定数量的破折号绘制一个单独的刻度线(并且在刻度线之后打印一个可选的字符串标签) 。
最重要的工作是由递归函数 draw_interval 来完成的。这个函数根据刻度间隔中中央刻度线的长度来绘制刻度间隔之间副刻度线的序列。根据本节开始时列出的 \(L \ge 1\) 的规律,当出现 \(L=0\) 这个基本情况,不再绘制任何东西。对于 \(L \ge 1\), 第一步和最后一步都是通过递归调用 draw_interval (L-1) 进行的,中间的步骤是通过递归调用函数 draw_interval(L) 进行的。
def draw_line(tick_length, tick_label=''):
"""Draw one line with given tick length (followed by optional label)."""
line = '-' * tick_length
if tick_label:
line += ' ' + tick_label
print(line)
def draw_interval(center_length):
"""Draw tick interval based upon a central tick length."""
if center_length > 0: # stop when length drops to 0
draw_interval(center_length - 1) # recursively draw top ticks
draw_line(center_length) # draw center tick
draw_interval(center_length - 1) # recursively draw bottom ticks
def draw_ruler(num_inches, major_length):
"""Draw English ruler with given number of inches and major tick length."""
draw_line(major_length, '0') # draw inch 0 line
for j in range(1, 1 + num_inches):
draw_interval(major_length - 1) # draw interior ticks for inch
draw_line(major_length, str(j)) # draw inch j line and label
用递归追踪说明标尺的绘制¶
用一个递归追踪可以使递归函数 draw_interval 的执行变得可视化。然而, draw_ interval 的追踪比阶乘函数追踪的例子更复杂,因为每个实例进行了两次递归调用。为了说明这一点,我们将以排列的形式展示递归跟踪,这个形式非常类似一个文档大纲,如图 4-3 所示
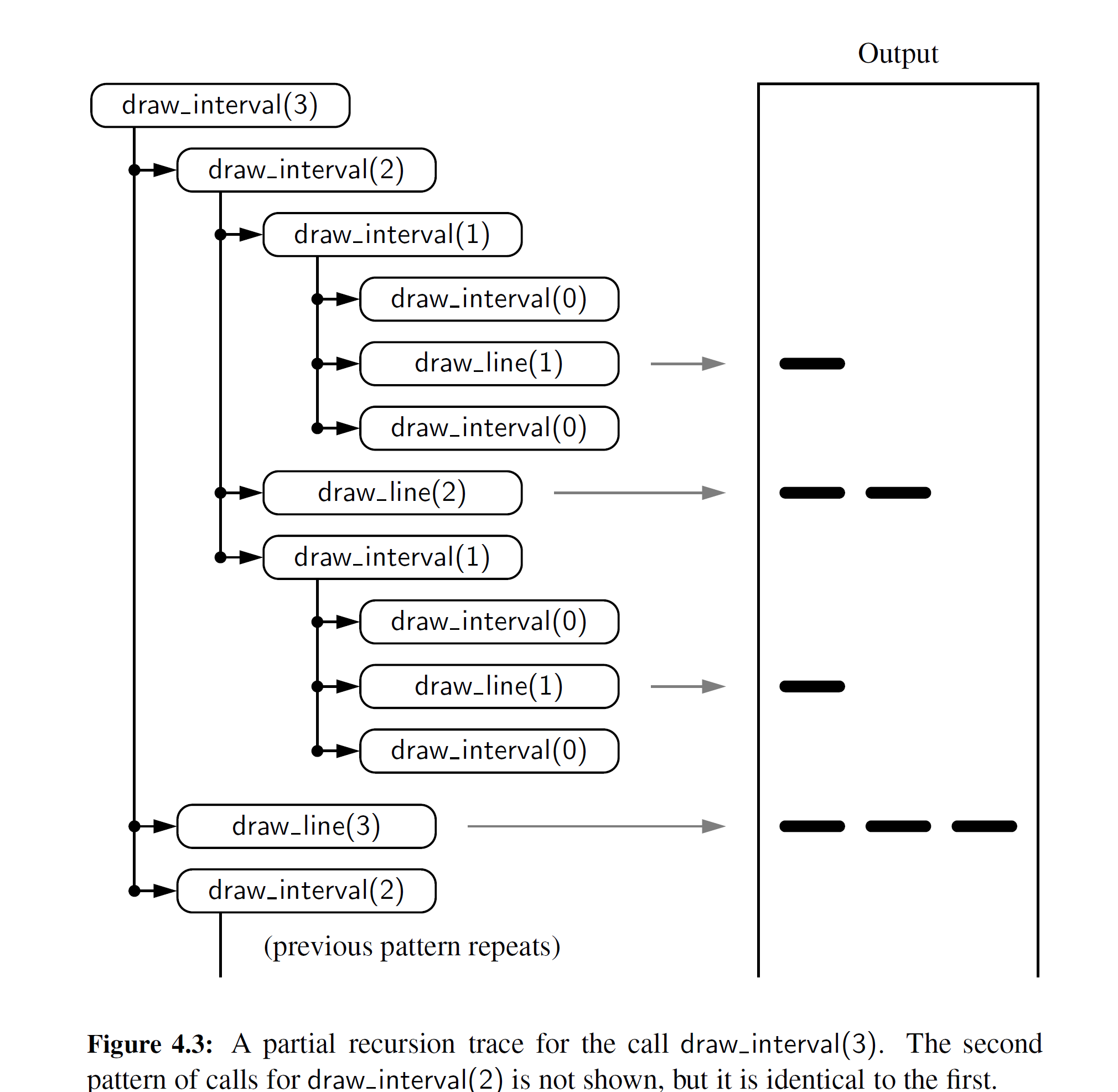
可以看到,递归在 python 中的执行仍然是按照“顺序”进行的
4.1.3 二分查找¶
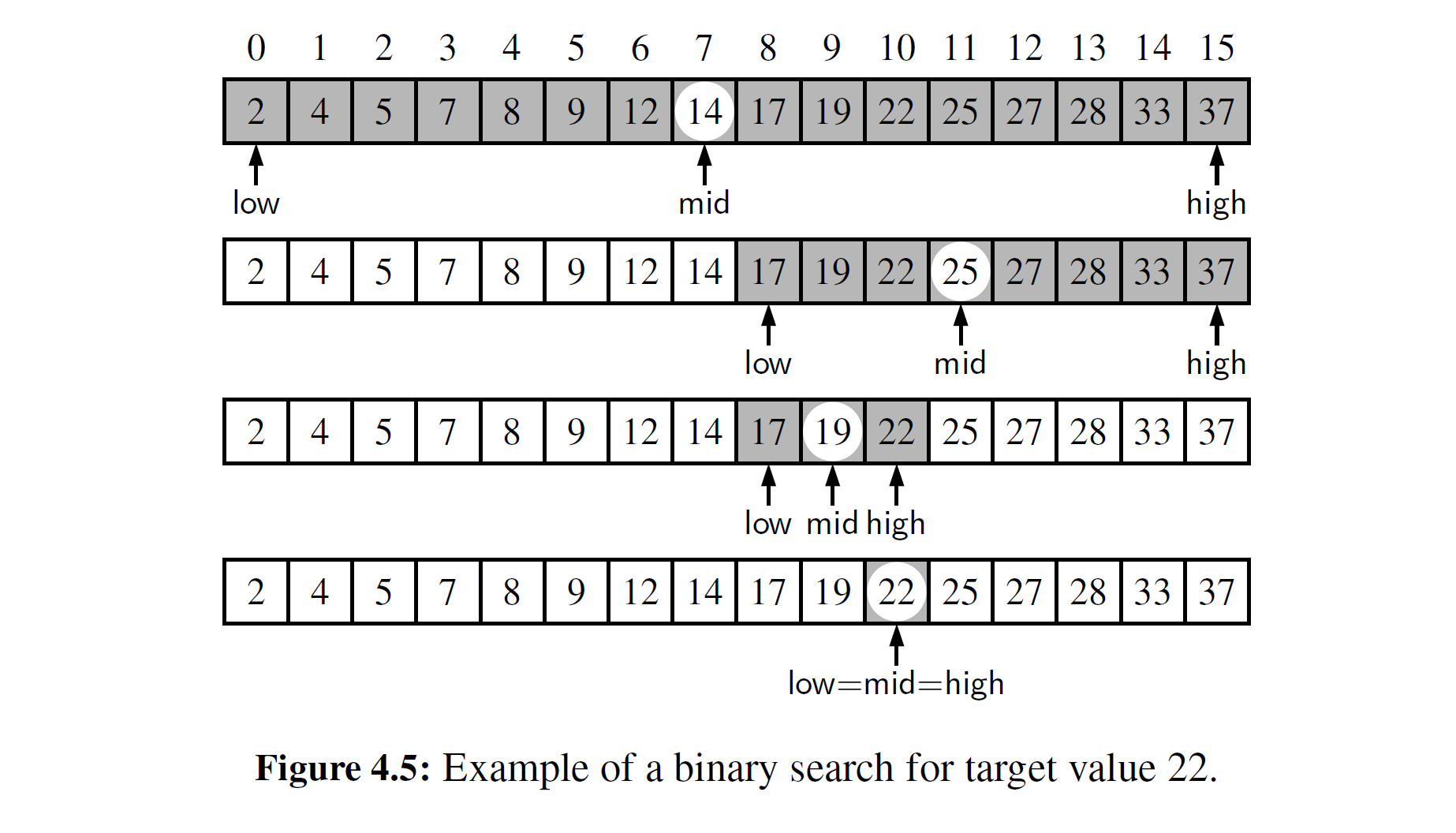
本节将介绍一个典型的递归算法——二分查找。该算法用于在一个含有 n 个元素的有序序列中有效地定位目标值。这是最重要的计算机算法之一,也是我们经常顺序存储数据(见图 4-4) 的原因

当序列无序时,寻找一个目标值的标准方法是使用循环来检查每一个元素, 直至找到目标值或检查完数据集的每个元素。这就是所谓的顺序查找算法。因为最坏的情况下每个元素都需要检查,这个算法的时间复杂度是 O(n) (即线性的时间) 。
当序列有序并且可通过索引访问时,有一个更有效的算法(直觉上,想想你如何手工完成这个任务!) 。对于任意索引 \(j\), 我们知道在索引 \(0, … ,j-1\) 上存储的所有值都小于索引 j 上的值, 并且在索引 \(j + 1, …,n - 1\) 上存储的所有值都大于或等于索引 j 上的值。在搜索 目标时,这种观察使我们能够迅速定位目标值。在查找时,如果不能排除一个元素与目标值相匹配,那么称序列的这个元素为候选项。该算法维持两个参数 low 和 high, 这样可使所有候选条目的索引位于 low 和 high 之间。首先, low = 0 和 high= n - 1 。然后我们比较目标值和中间值候选项,即索引项 [mid] 的数据
考虑以下三种情况:
- 如果目标值等于 [mid] 的数据,然后找到正在寻找的值,则查找成功并且终止。
- 如果目标值 < [mid] 的数据,对前半部分序列重复这一过程, 即索引的范围从 low 到 mid- 1 。
- 如果目标值>[mid] 的数据,对后半部分序列重复这一过程,即索引的范围从 mid + 1 到 high 。
如果 low > high , 说明索引范围 [low, high] 为空, 则查找不成功。
该算法被称为二分查找。代码段 4-3 给出了一个 python 实例,其算法执行过程的说明如图 4-5 所示。而顺序查找的时间复杂度是 O(n) ,更为高效的二分查找的时间复杂度是 O(log n) 。这是一个显著的改进,因为假设 n 是十亿, log n 仅为 30 。(对于二分查找运行时间的问题, 我们将在 4.2 节命题 4-2 做正式的分析。)
def binary_search(data, target, low, high):
"""Return True if target is found in indicated portion of a python list.
The search only considers the portion from data[low] to data[high] inclusive.
"""
if low > high:
return False # interval is empty; no match
else:
mid = (low + high) // 2
if target == data[mid]: # found a match
return True
elif target < data[mid]:
# recur on the portion left of the middle
return binary_search(data, target, low, mid - 1)
else:
# recur on the portion right of the middle
return binary_search(data, target, mid + 1, high)
4.1.4 文件系统¶
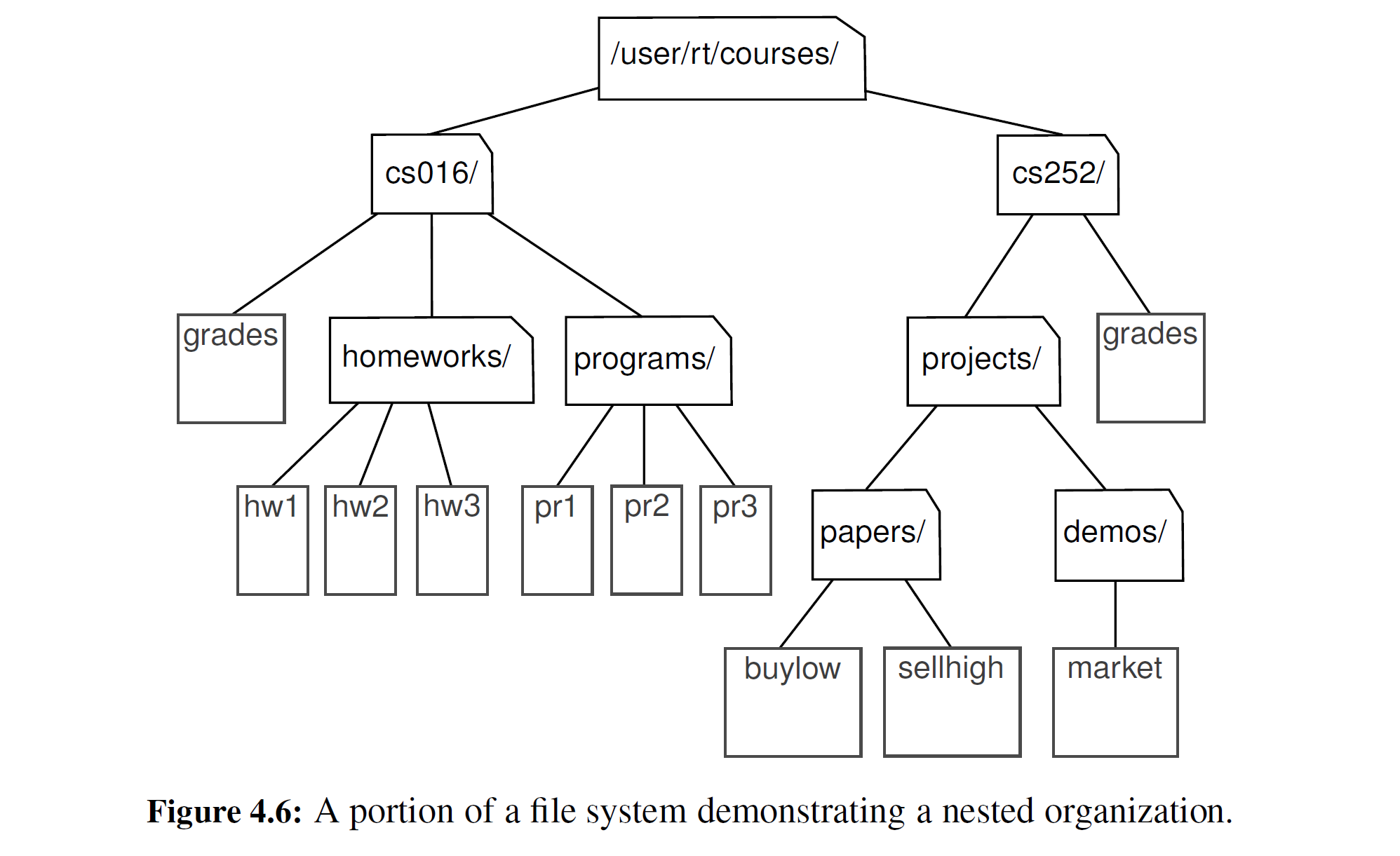
现代操作系统用递归的方式来定义文件系统目录(有时也称为“文件夹") 。也就是说,一个文件系统包括一个顶级目录,这个目录的内容包括文件和其他目录,其他目录又可以包含文件和其他目录,以此类推。虽然必定会有一些基本的目录只包含文件而没有下一级子目录,但是操作系统允许嵌套任意深度的目录(只要在内存中有足够的空间) 。图 4-6 所示即为此类文件系统的一部分。
考虑到文件系统表示的递归特性,操作系统中许多常见的行为,比如目录的复制或删除,都可以很方便地用递归算法来实现。在本节中,我们考虑这样一个算法: 计算嵌套在一个特定目录中的所有文件和目录的总磁盘使用情况。
为了说明空间的使用情况,图 4-7 显示了样例文件系统中所有条目使用的磁盘空间。我们对每个条目所使用的即时磁盘空间以及由该条目和所有嵌套目录所使用的累计磁盘空间加以区分。例如,目录 cs016 仅仅使用了 2K 的即时空间,但使用了 249K 的累计磁盘空间。
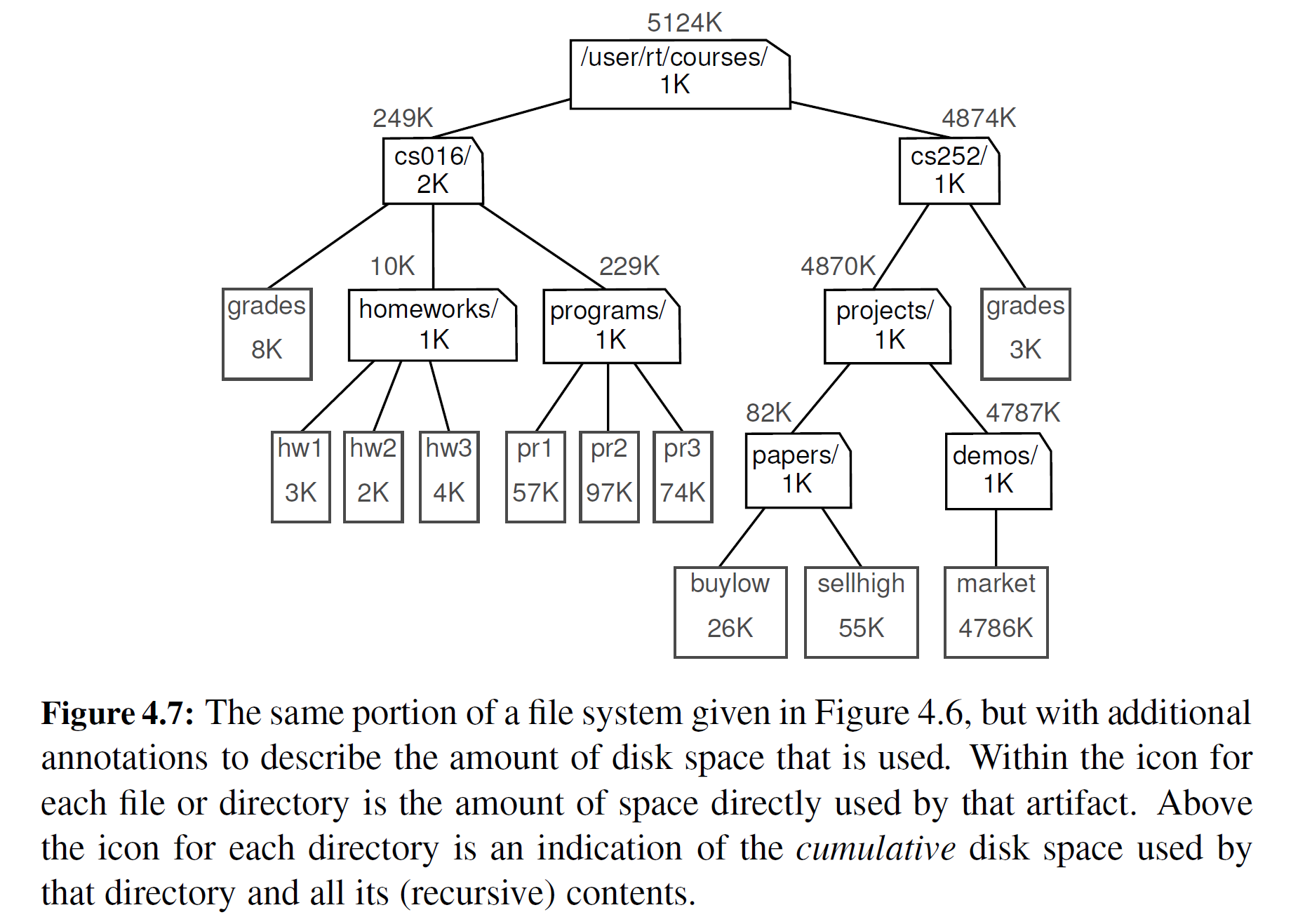
一个条目的累计磁盘空间可以用简单的递归算法来计算。它等于条目使用的直接磁盘空间加上直接存储在该条目中所有条目使用的累计磁盘空间之和。例如, cs016 的累计磁盘空间是 249K, 因为它本身使 用 2K 的磁盘空间, grades 使用 8K 的累计磁盘空间, homeworks 使用 10K 的累计磁盘空间, programs 使用 229K 的累计磁盘空间。代码段 4-4 给出了这个算法的伪代码。
Algorithm DiskUsage(path):
Input: A string designating a path to a file-system entry
Output: The cumulative disk space used by that entry and any nested entries
total = size{path) {immediate disk space used by the entry}
if path represents a directory then
for each child entry stored within directory path do
total = tota l+ DiskUsage(child) { recursive call }
return total
python 的操作系统模块¶
为了给出一个计算磁盘使用情况的递归算法 python 实例,我们需要借助 python 的操作系统模块, 在程序执行的过程中, 该模块提供了强大的与操作系统交互的工具。这是一个丰富的函数库,但我们只需要以下四个函数:
os.path.getsize(path)
返回由字符串路径(例如: user/rt/courses) 标识的文件或者目录使用的即时磁盘空间大小(单位是字节) 。
os.path.isdir(path)
如果字符串路径指定的条目是一个目录,则返回 True; 否则, 返回 false
os.listdir(path)
返回一个字符串列表,它是字符串路径指定的目录中所有条目的名称。在样例文件系统中, 如果参数是 /user/rt/courses, 那么返回字符串列表['cs016' , 'cs252']
os.path.join(path, filename)
生成路径字符串和文件名字符串,并使用一个适当的操作系统分隔符在两者之间分隔(例如: Unix/Linux 系统中的 '/' 字符和 Windows 系统中的 '\' 字符) 。返回表示文件完整路径的字符串
通过使用 OS 模块, 现在我们把代码段 4-4 中的算法转换成代码段 4-5 中的 python 实例。
import os
def disk_usage(path):
"""Return the number of bytes used by a file/folder and any descendents."""
total = os.path.getsize(path) # account for direct usage
if os.path.isdir(path): # if this is a directory,
for filename in os.listdir(path): # then for each child:
childpath = os.path.join(path, filename) # compose full path to child
total += disk_usage(childpath) # add child's usage to total
print ('{0:<7}'.format(total), path) # descriptive output (optional)
return total # return the grand total
递归追踪¶
为了产生另一种格式的递归跟踪,我们在 python 实例加入了额外的 print 语句( 代码段 4-5 的第 11 行) 。该输出的准确格式有意模仿由一个名为 du 的典型的 Unix/Linux 实用程序(对于“ disk usage") 生成的输出。如图 4-8 所示,它报告一个目录及其中嵌套的所有内容使用的磁盘空间的总盘,并能生成详细的报告。

在图 4- 7 所示的样例文件系统上执行时, disk_usage 函数的实例产生一个相同的结果。在算法执行期间,对于文件系统的每一个条目,正好使用一次递归调用。因为 print 语句是在递归调用之前执行的,所以图 4- 8 所示的输出反映了递归调用完成的顺序。需要特别强调的是,在可以计算和报告所有包含的条目的累计磁盘空间之前,我们==必须完成嵌套在该条目之下的所有条目的递归调用==。例如,我们在计算包含 grades 、homeworks 和 programs 条目的递归调用完成后,才知道条目 user/rt/courses/cs016 的累计磁盘空间大小
4.2 分析递归算法¶
在第 3 章中,我们介绍了一种分析算法效率的数学方法,该方法基于算法执行的基本操作次数的估计值。我们使用符号(比如 big-Oh) 来概括操作次数和问题输入大小之间的关系。本节将演示如何执行这种类型的递归算法的时间复杂度分析。
对于递归算法,我们将解释基于函数的特殊激活并且被执行的每个操作,该函数在被执行期间管理控制流。换句话说,对于每次函数调用,我们只解释被调用的主体内执行的操作的数目。然后,通过在每个单独调用过程中执行的操作数的总和,即所有调用次数,我们可以解释被作为递归算法的一部分而执行的操作的总数。(顺便说一句,这也是我们分析非递归函数的方式。这些非递归函数从它们的函数体中调用其他函数)
为了说明这种分析的模式,我们回顾一下 4.1.1 ~ 4.1.4 节介绍的四个递归算法:阶乘函数、绘制一个英式标尺、二分查找以及文件系统累计磁盘空间大小的计算。一般来说,在识别有多少递归调用发生,以及每个调用的参数化可以用来估计其调用的主体内发生的基本操作次数方面,我们可以借助于递归追踪提供的客观事实。但是,每一个递归算法都具有独特的结构和形式
计算阶乘¶
正如 4.1.1 节所描述的,分析计算阶乘的函数的效率是比较容易的。图 4-1 给出了阶乘函数的一个示例递归追踪。为了计算 factorial(n) ,共执行了 n + 1 次函数调用。参数从第一次调用时的 n 下降到第二次调用时的 n - 1, 以此类推,直至达到参数为 0 时的基本情况。代码段 4-1 给出了函数体的检测,同样清楚的是,阶乘的每个调用执行了一个常数级别的运算。因此,我们得出这样的结论:计算 factorial(n) 的操作总次数是 O(n) ,因为有 n + 1 次函数的调用,所以每次调用占的操作次数为 O(1) 。
绘制一个英式标尺¶
在 4.1.2 节分析英式标尺的应用程序中,我们考虑共有多少行输出这一基本问题。该输出是通过初始调用 drawinterval(c) 产生的,其中 c 表示中央刻度线长度。这是该算法的整体效率的合理基准,因为输出的每一行是基于一个对 draw_line 函数的调用,以及对 draw interval 的每次非零参数递归调用恰好产生一个对 draw_line 的直接调用。
通过检验源代码和递归追踪可以获得直观认识。我们知道对 draw_interval(c) (c > 0) 的一个调用产生两个对 draw_interval(c - 1) 的调用和一个单独的 draw_line 的调用。我们将依赖这些客观事实来证明以下的声明
命题 4-1: 对于 \(c\ge 0\), 调用 draw_interval(c) 函数刚好产生 \(2^c - 1\) 行输出
证明:通过归纳法(参见 3.4.3 节),我们给出了这种声明的正式证明。事实上,归纳法是用于证明递归过程正确性和有效性的自然数学技术。在标尺的这个例子中,我们注意到,draw_ interval(0) 的应用程序没有输出, 并以此作为证明的基本情况。
更一般的是,通过调用 draw_interval(c) 函数打印的行数比通过调用 draw_interval(c - 1)函数产生的行数的两倍还多 1——因为在两个这样的递归调用之间会打印一个中心线。通过归纳法,我们计算出行数 \(1 + 2(2^{c - 1} - 1) = 1+ 2^c - 2 = 2^c - 1\) 。
这个证明表明, 一个更严格的被称为递归方程的数学工具可用于分析递归算法的运行时间。在 12.2.4 节对递归排序算法的分析中,我们会讨论这种技术。
执行二分查找¶
如在 4.1.3 节提到的,考虑到二分查找算法的运行时间,我们观察到二分查找方法的每次递归调用中被执行的基本操作次数是恒定的。因此,运行时间与执行递归调用的数量成正比。我们会证明在对含有 n 个元素的队列进行二分查找过程中至多进行 \(\left\lfloor\log n\right\rfloor+ 1\) 次递归调用,并且得出以下声明。
命题 4-2: 对于含有 n 个元素的有序序列, 二分查找算法的时间复杂度是 \(O(\log n)\)
证明: 为了证明这一命题, 一个重要的事实是:在每次递归调用中,需要被查找的候选条目的数量是由一个值给出的。这个值为
此外,每次递归调用之后,剩下的候选条目的数量至少减少一半。具体来讲,从 mid 的定义可知,剩下的候选条目的数量是
或者是
候选条目最初为 n ; 在进行一次二分查找调用之后,它至多是 n/2 ; 在进行第二次调用后,它至多为 n/4; 以此类推。一般情况下,在进行第 j 次二分查找调用之后,剩下的候选条目的数量至多是 \(n/2^j\) 在最坏的情况下( 一次不成功的查找), 当没有更多的候选条目时递归调 用停止。因此,进行递归调用的最大次数,有最小整数 r, 使得
换言之(回想一下, 当对数底数是 2 时,省略对数底数), \(r > \log n\) 。因此,有 \(r = \left\lfloor\log n\right\rfloor+ 1\) ,这意味着二分查找的时间复杂度为 \(O(\log n)\)
计算磁盘空间使用情况¶
4.1 节最后一个递归算法是计算在文件系统的特定部分整体磁盘空间使用情况。为了描述所分析的”问题大小",我们用 n 表示所考虑文件系统的特定部分的文件系统条目的数量。(例如,图 4-6 所示的文件系统有 n(n = 19) 个条目)
为了描述 disk_usage 函数初始调用的累计时间开销,我们必须分析所执行的递归调用的总数以及在这些调用中执行的操作次数。
首先显示刚好有 n 次函数调用的递归过程,尤其是文件系统的相关部分的每个条目对应一次递归调用的过程。直观来讲,这是因为对于文件系统的特定条目 e 仅进行一次 disk_ usage 调用,在代码段 4-5 的 for 循环中处理包含 e 的父目录时,将只检索一次该条目。
为了形式化地证明上述论证,我们可以定义每个条目的嵌套级别,比如定义起始条目的嵌套级别为 0, 定义直接存储在该条目中所有条目的嵌套级别为 1 , 定义存储在这些条目中所有条目的嵌套级别为 2, 以此类推。我们可以通过归纳法证明在嵌套等级为 K 的各条目上恰好有一个对 disk_usage 函数的递归调用。作为一种基本情况, 当 k = 0 时,唯一进行的递归调用是初始调用。就归纳步骤来说, 一旦知道在嵌套级别为 k 的每个条目上恰好只有一次递归调用,我们可以证明对于嵌套级别为 k 的条目下的条目 e, 仅从处理包含 e 的 k + 1 级条目的 for 循环中调用一次
确定文件系统的每个条目都有一个递归调用后,我们回到算法的总计算时间问题。如果我们可以证明我们在函数的任何一次调用中花费了 O(1) 时间,那就太好了,但事实并非如此。 虽然在对 os.path.getsize 的调用中仅有恒定数量的步骤来计算该条目的磁盘使用情况,但当条目是一个目录时,disk_usage 函数的主体包括一个遍历所有该目录中包含的条目的 for 循环 。 在最坏的情况下,一个条目可能包含 n-1 个其他条目
基于这种推理,我们可以得出这样的结论: 有 O(n) 个递归调用, 并且每个调用运行的时间为 O(n)(这指的均是“最坏情况”,与 n 的多少并无关系) ,从而导致总的运行时间为 \(O(n^2)\) 。虽然这个时间上限在技术上是正确的, 但它不是一个严格意义上的上限。值得注意的是,我们可以证明更强的约束:对于 disk_ usage 函数的递归算法可以在 O(n) 的时间内完成!较弱的约束是悲观的, 因为它假设了每个目录所有条目在最坏情况下的数量。虽然可能一些目录包含的条目数量与 n 成正比, 但它们不可能每个都含有那么多的条目。为了证明这个更有力的声明,我们选择考虑在所有递归调用中 for 循环迭代的总数。我们断言刚好有 n - 1 个该循环的这种迭代。这一声明基于这样一个事实,即该循环的每次迭代进行一次对 disk_usage 函数的递归调用,并且已经得出结论,即对 disk_usage 函数共进行了 n 次调用(包括最初的调用) 。因此,我们得出这样的结论:有 O(n) 次递归调用,每次递归调用==在循环外部使用 O(1) 的时间,并且循环操作的总数是 O(n)== 。总结所有这些限制条件,操作的总数是 O(n)
我们已经得出的观点比前面递归的例子更先进。有时可以通过考虑累积效应获得一系列操作更严格的约束,而不是假设每个操作都是最坏的情况,这种思想就是被叫作分期偿还的技术(在 5.3 节我们会看到更多的例子) 。此外,文件系统是隐式地使用“树”这一数据结构的例子,磁盘使用(disk usage ) 算法实际是树遍历算法的一种表现。树是第八章的重点,并且关于磁盘使用( disk usage ) 算法时间复杂度是 O(n) 这一论证将在 8.4 节中树的遍历中加以推广。
4.3 递归算法的不足¶
虽然递归是一种非常强大的工具,但它也很容易被误用。在本节中, 我们检查了几个问题,其中一个糟糕的递归实现导致严重的效率低下,并讨论了一些用于识别和避免这种陷阱的策略。
我们首先重新审视第 3.3.3 节定义的元素唯一性问题。 我们可以使用以下递归公式来确定序列的所有 n 个元素是否都是唯一的。 作为基本情况,当 n = 1 时,该元素显然是唯一的。 对于 n ≥ 2,元素是唯一的当且仅当该集合的前 n−1 个元素是唯一的,并且该集合的最后 n−1 个元素是唯一的(因为这是唯一一对子情况中没有被检查的元素) 。代码段 4-6 给出了基于这种思想的递归实例,称其为 unique3 (与第 3 章的 unique1 和 unique2 区分开来) 。
def unique3(S, start, stop):
"""Return True if there are no duplicate elements in slice S[start:stop]."""
if stop - start <= 1: return True # at most one item
elif not unique3(S, start, stop-1): return False # first part has duplicate
elif not unique3(S, start+1, stop): return False # second part has duplicate
else: return S[start] != S[stop-1] # do first and last differ?
不幸的是,这是一个效率非常低的递归使用。非递归部分的每次调用所使用的时间为 O(1), 所以总的运行时间将正比于递归调用的总数。为了分析这个问题,我们用 n 表示所考虑的条目总数,即 n = stop - start
如果 n = 1, 则 unique3 的运行时间为 O(1),因为在这种情况下,不进行递归调用。一般情况下,最重要的发现是,对于一个大小为 n 的问题,对 unique3 函数的单一调用可能导致对两个大小为 n-1 的问题的 unique3 函数调用。反过来,这两个大小为 n - 1 的调用可能又产生 4 个大小为 n -2 的调用(各两个),然后是 8 个大小为 n-3 的调用,以此类推。因此在最坏的情况下,函数调用的总数由如下几何求和公式给出
这等于是由命题 3-5 给出的。因此函数 unique3 的时间复杂度为 \(O(2^n)\) 。难以置信,这个函数解决元素唯一性问题的效率如此低下。其低效率不是因为使用递归,而是缘于所使用的递归不佳这样一个事实,这是我们在练习 C-4 .11 中要解决的问题
一个低效的计算斐波那契数的递归算法¶
在 1.8 节中,我们介绍了生成斐波纳契数的过程,可以递归地定义如下:
恰巧, 基于上述定义的直接实现就是代码段 4-7 中所示的函数 bad_fibonacci, 该函数通 过执行两个非基本情况的递归悯用来计算斐波纳契数。
def bad_fibonacci(n):
"""Return the nth Fibonacci number."""
if n <= 1:
return n
else:
return bad_fibonacci(n-2) + bad_fibonacci(n-1)
不幸的是,这样的斐波那契数公式的直接实现会导致函数的效率非常低。以这种方式计算第 n 个斐波纳契数需要对这个函数进行指数级别的调用。具体来说,用 \(C_n\) 表示在 bad fibonacci(n) 执行中进行的调用次数。然后,我们可以得到以下的一系列值:
如果遵循这个模式继续下去,我们可以看到,对于每两个连续的指标, 后者调用的数量将是前者的 2 倍以上。也就是说, \(c_4\) 是 \(c_2\) 的两倍以上, \(c_5\) 是 \(c_3\) 的两倍以上, \(c_6\) 是 \(c_4\) 的两倍 以上,以此类推。因此 \(c_n > 2^{n/2}\) 意味着 bad_fibonacci(n) 使得调用的总数是 n 的指数级
一个高效的计算斐波那契数列的递归算法¶
我们之所以尝试使用这个不好的递归公式, 是因为第 n 个斐波那契数取决于前两个值,即 \(F_{n -2}\) 和 \(F_{n - 1}\) 。但是请注意,计算出 \(F_{n-2}\) 之后,计算 \(F_{n-1}\) 的调用需要其自身递归调用以计算 \(F_{n-2}\) , 因为它不知道先前级别的调用中被计算的 \(F_{n - 2}\) 的值。这是一个重复的操作。更 糟的是,这两个调用都需要(重新)计算 \(F_{n - 3}\) 的值, \(F_{n-1}\) 的计算也一样。正是这种滚雪球效应,导致 bad_fibonacci 函数有指数倍的运行时间。
我们可以更有效地使用递归来计算 \(F_n\),这种递归的每次调用只进行一次递归调用。要做到这一点. 我们需要重新定义函数的期望值。我们定义了一个递归函数,该函数返回一对连续的斐波那契数列 \((F_n, F_{n-1})\) ,并且使用约定 \(F_{n - 1 }= 0\), 而不是让函数返回第 n 个斐波那契数这一单一数值。用返回一对连续的斐波那契数列代替返回一个值,虽然这似乎是一个更大 的负担,但从递归这一级来看,通过这个额外的信息之后使得递归更容易继续这一进程(它可以让我们避免再计算第二个值,这个值在递归中是已知的) 。代码段 4-8 给出了基于这种策略的一个实例。
def good_fibonacci(n):
"""Return pair of Fibonacci numbers, F(n) and F(n-1)."""
if n <= 1:
return (n,0)
else:
(a, b) = good_fibonacci(n-1)
return (a+b, a)
就效率而言,对于这个问题,效率低的递归和效率高的递归之间的区别就像黑夜和白天。bad_fibonacci 函数使用指数数量级的时间。我们认为函数 good_fibonacci (n) 使用的时间为 O(n) 。每次对 good_fibonacci(n) 函数的递归询用都使参数 n 减小 1 因此,递归追踪包括一系列的 n 个函数调用。因为每个调用的非递归工作使用固定的时间,所以整体的运算执行在 O(n) 的时间内完成。
python 中的最大递归深度¶
在递归的误用中,另一个危险就是所谓的无限递归。如果每个递归调用都执行另一个递归调用,而最终没有达到一个基本情况,那我们就有一个无穷级数的此类调用。这是一个致命的错误。无限递归会迅速耗尽计算资源,这不仅是因为 CPU 的快速使用,而且是由于每个连续的调用会创建需要额外内存的活动记录。一个明显不合语法的递归示例如下:
def fib( n):
return fib(n) # fib(n) equals fib(n)
然而,还有更微小的错误会导致无限递归。回顾我们在代码段 4-3 中二分查找的实现,在最后的情况下( 第 17 行),我们在序列的右半部分,特别是索引从 mid + 1 到 high 这部分,进行一个递归调用。那一行反而被写成
return binary_search(data, target, mid, high) # 注意 mid 的使用
这可能导致一个无限递归。尤其是在搜索范围内的两个元素时,有可能在同一范围内进行递归调用。
程序员应该确保每个递归调用以某种方式逐步向基本情况发展(例如,通过使用随每次调用减少的参数值) 。然而,为了避免无限递归, python 的设计者做了一个有意的决定来限制可以同时有效激活的函数的总数。这个极限的精确值取决于 python 分配,但典型的默认值是 1000 。如果达到这个限制, python 解释器就生成了一个 RuntimeError 消息:超过最大递归深度(maximum recursion depth exceeded )
对于许多合法的递归应用, 1000 层嵌套函数的限制调用足够了。例如, binary_search 函数( 见 4.1.3 节)的递归深度为 O(log n) ,所以要达到默认递归的限制, 需要有 \(2^{1000}\) 个元 素(远远超过宇宙中原子数最的估计值) 。然而,在下一节中,我们将讨论一些递归深度与 n 成正比的算法。python 在递归深度上的人为限制可能会破坏这些其他的合法计算。
幸运的是, python 解释器可以动态地重置,以更改默认的递归限制。这是用一个名为 sys 的模块来实现的,该模块支持getrecursionlimit 函数和 setrecursionlimit 函数。这些函数的使用示例如下:
import sys
old = sys.getrecursionlimit() # perhaps 1000 is typical
sys.setrecursionlimit(lOOOOOO) # change to allow 1 million nested calls
4.4 递归的其他例子¶
本章的剩余部分将给出使用递归的其他例子。我们通过考虑在一个激活的函数体内开始的递归调用的最大数量来组织我们的介绍
- 如果一个递归调用最多开始一个其他递归调用,我们称之为线性递归(linear recursion) 。
- 如果一个递归调用可以开始两个其他递归调用, 我们称之为二路递归(binary recursion ) 。
- 如果一个递归调用可以开始三个或者更多其他递归调用,我们称之为多重递归 ( multiple recursion) 。
4.4.1 线性递归¶
如果一个递归函数被设计成使得所述主体的每个调用至多执行一个新的递归调用,这被称为线性递归。到目前为止,在我们已经看到的递归函数中,阶乘函数的实现(见 4.1.1 节) 和 good_fibonacci 函数(见 4.3 节)是线性递归鲜明的例子。更有趣的是,尽管在名称中有 " binary ", 二分查找算法(见 4.1.3 节)也是线性递归的一个例子。二分查找的代码(见代码段 4-3) 包括一个具有两个分支的情况分析,这两个分支产生递归调用,但在函数体的一个具体执行期间只有其中一个调用可以被执行。
正如在 4.1.1 节描绘的阶乘函数(见图 4 -1 ) 一样,线性递归定义的一个结果是任何递归追踪将表现为一个单一的调用序列。注意,线性递归术语反映递归追踪的结构,而不是运行时间的渐近分析,例如,我们已经看到二分查找的时间复杂度为 O(log n) 。
元素序列的递归求和¶
线性递归可以作为一个有用的工具来处理数据序列,例如 python 列表。例如,假设想要计算一个含有 n 个整数的序列 S 的和。我们可以使用线性递归解决这个求和问题。通过观察发现,如果 n = 0 , S 中所有 n 个整数的总和是 0; 否则,序列 S 的和应为 S 中的前 n - 1 个整数的总和加上 S 中最后一个元素(见图 4-9) 。

基于这个客观事实,代码段 4-9 实现了计算数字序列和的递归算法
def linear_sum(S, n):
"""Return the sum of the first n numbers of sequence S."""
if n == 0:
return 0
else:
return linear_sum(S, n-1) + S[n-1]
图 4-10 给出了 linear_sum 函数递归追踪的一个小例子。对于大小为 n 的输入, linear_sum 算法执行了 n + 1 次函数调用。因此, 这将需要 O(n) 的时间, 因为它花费恒定的时间执行每次调用的非递归部分。此外, 我们还可以看到,这个算法使用的内存空间 (除了序列 S ) 也是 O(n) ,正如在做出最后一 次的递归调用(当 n = 0 ) 时的递归追踪中, 对 n + 1 个活动记录的任何一个我们都使用固定数量的内存空间

接下来,让我们考虑逆置含有 n 个元素 的序列 S 的问题,即第一个元素成为最后一 个元素,第二个元素成为倒数第二个元素, 以此类推。我们可以使用线性递归解决这个问题,通过观察,可以通过对调第一个元素和最后一个元素,之后递归地反置剩余元组,这样就可以完成序列的逆置。按照约定,我们把第一次调用的算法记作 reverse(S, 0 , len(S)) 。代码段 4-10 给出了这个算法的一个实现。
def reverse(S, start, stop):
"""Reverse elements in implicit slice S[start:stop]."""
if start < stop - 1: # if at least 2 elements:
S[start], S[stop-1] = S[stop-1], S[start] # swap first and last
reverse(S, start+1, stop-1) # recur on rest
需要注意的是,有两个隐含的基本情况场景: start == stop 时,这个隐含的范围是空的; 当 start == stop - 1 时,这个隐含的范围仅含有一个元素。这两种情况中的任何一个,都不需要再执行任何操作,因为含有零个或者一个元素的序列与它的逆置序列是完全相等的。当 其他情况调用递归时,我们都保证使过程朝着一个基本情况发展,不同的是, stop - start 每次调用减小两个值 (见图 4-11 ) 。如果 n 是偶数,最终将达到 start == stop 这 种情况;如果 n 是奇数,最终会达到 start == stop - 1 这 种情况。
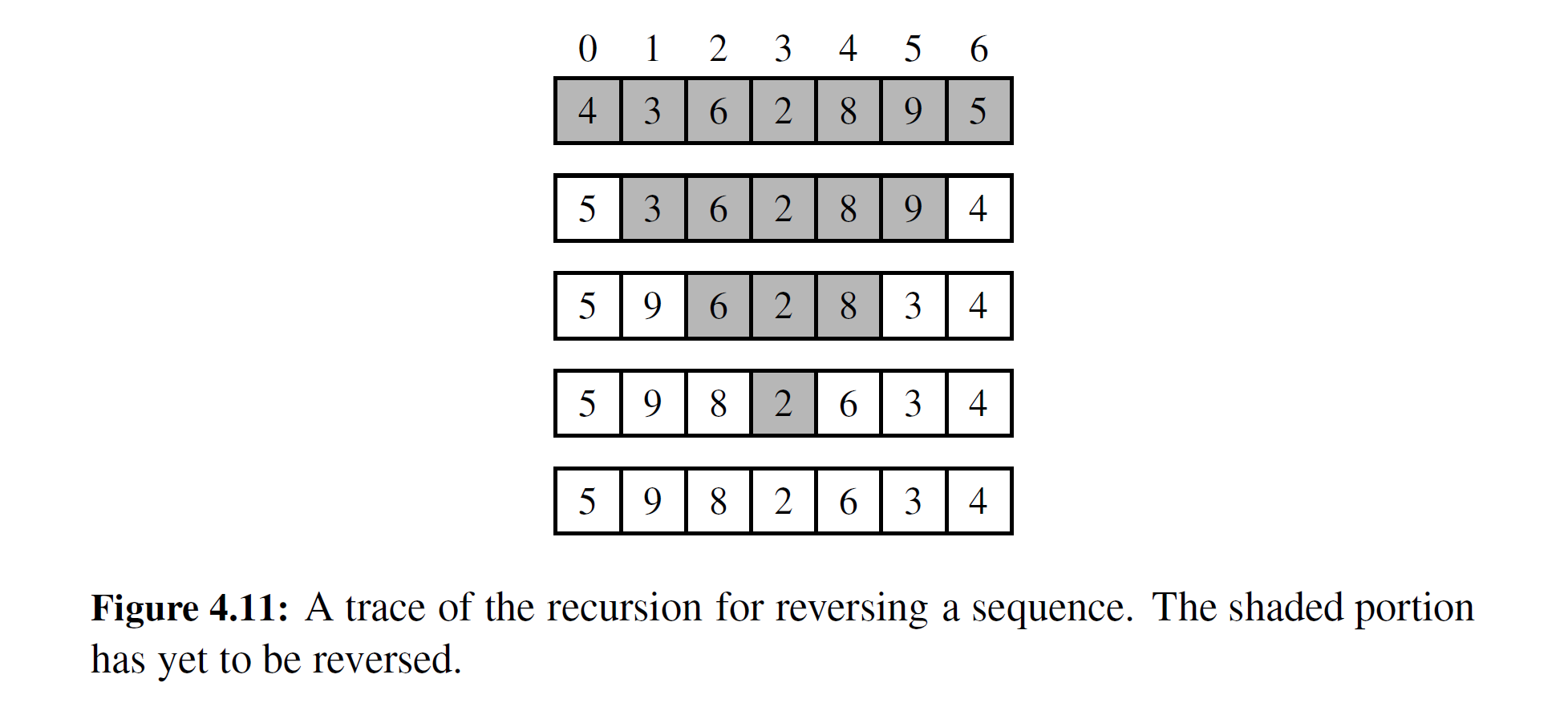
上面的观点意味着代码段 4-10 的递归算法确保在进行 \(1+\left\lfloor\frac n2\right\rfloor\) 次递归调用后递归终止。因为每次调用包含固定数量的工作,所以整个过程运行时间为 O(n) 。
用于计算幂的递归算法¶
再举一个线性递归应用的例子,即数 x 的 n 次幂问题,其中 n 是任意的非负整数。也就 是说,我们希望计算幂函数( power function) ,其定义为 \(power(x, n) = x^n\)(我们在此讨论中使用名称 “power”,以区别于提供此类功能的内置函数 pow。)对于这个问题,我们将考虑两个不同的递归公式,这两个公式会导致算法有不同的性能。
一个简单的递归定义来自 \(x^n = x · x^{n−1}\) 对于 n > 0 的事实。
代码段 4-11 给出了这个定义产生的一个递归算法。
def power(x, n):
"""Compute the value x**n for integer n."""
if n == 0:
return 1
else:
return x * power(x, n-1)
这个版本的 power(x, n) 函数递归调用的时间复杂度为 O(n) 。它的递归追踪和图 4-1 中阶乘函数的递归追踪的结构非常相似,都是每次调用参数减 1,并且每 n + 1 层执行固定数量的工作。
但是,采用平方技术的替代定义可以更快地计算幂函数。 令 \(k =\left\lfloor\frac n2\right\rfloor\) 表示递归的层数(在 python 中表示为 n // 2)。 我们考虑表达式 \(\left(x^k\right)^ 2\)。当 n 为偶数时,\(\left\lfloor\frac n2\right\rfloor =\frac n2\),因此 \(\left(x^k\right)^ 2 = \left(x^{\frac n 2}\right)^ 2 = x^n\)。 当 n 为奇数时,\(\left\lfloor\frac n2\right\rfloor = \frac{n−1} 2\) 且 \(\left(x^k\right)^ 2 = x^{n−1}\),因此 \(x^n = x · \left(x^k\right)^ 2\),正如 213 = 2 · 26 · 26。通过这个分析,我们可以得出如下的递归定义:
如果要执行两个递归调用来计算 \(\text{power}\left(x,\left\lfloor\frac n2\right\rfloor\right)\cdot \text{power}\left(x,\left\lfloor\frac n2\right\rfloor\right)\),那么实现这个递归的追踪表示要进行 O(n) 次调用。我们可以通过计算 \(\text{power}\left(x,\left\lfloor\frac n2\right\rfloor\right)\)作为部分结果,然后乘以它本身来显着地减少执行的操作。代码段 4-12 给出了基于这种递归定义的一个示例。
def power(x, n):
"""Compute the value x**n for integer n."""
if n == 0:
return 1
else:
partial = power(x, n // 2) # rely on truncated division
result = partial * partial
if n % 2 == 1: # if n odd, include extra factor of x
result *= x
return result
为了说明改进算法的执行,图 4-12 给出了 计算 power(2, 13) 函数的递归追踪。
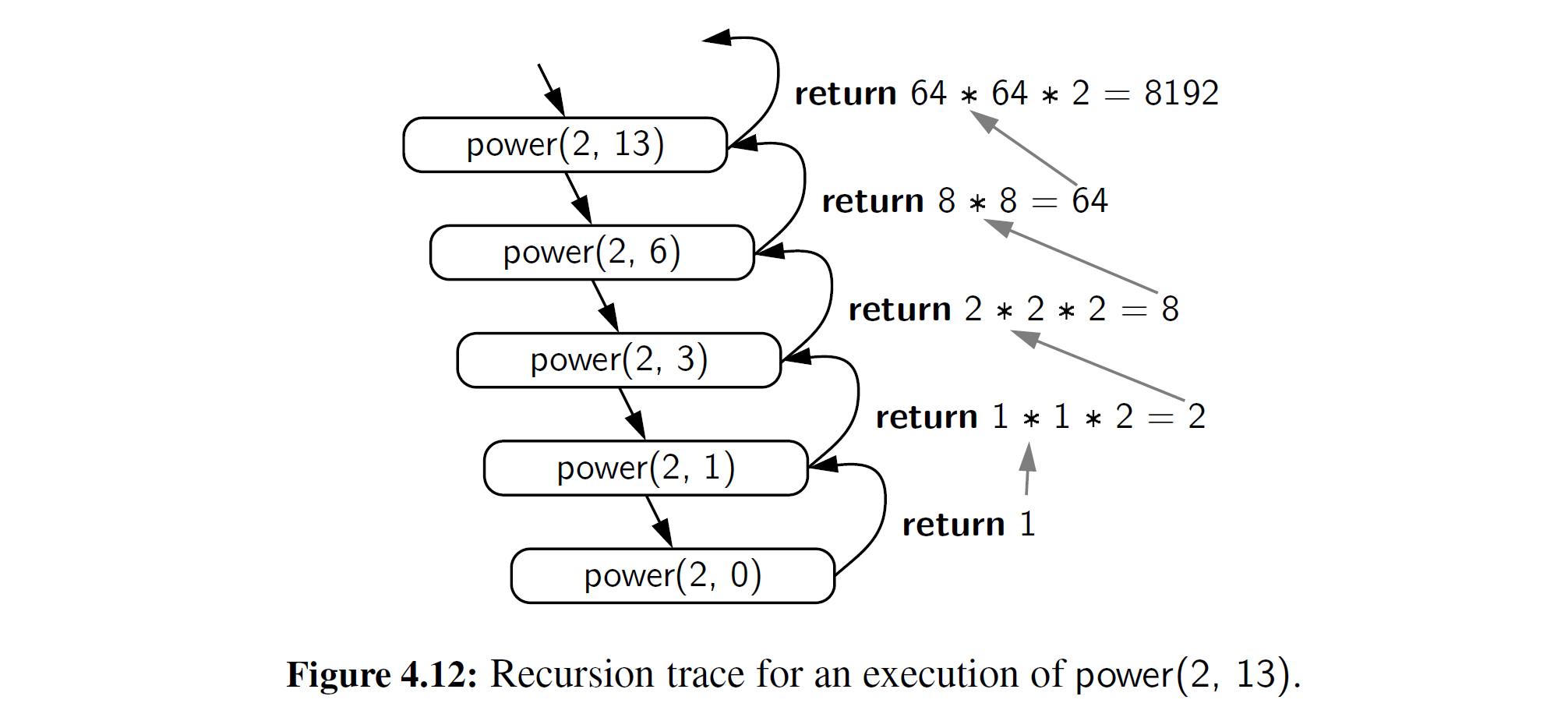
为了分析修正算法的运行时间,我们观察到函数 power(x, n) 每个递归调用中的指数最多是之前调用的一半。 如我们在二分查找的分析中 所看到的,在变成 1 或者更少之前,我们可以用 2 除 n 的时间的数量级是 O(log n) 。 因此,新构想的幂函数产生 O(log n) 次递归调用。 每个单独的函数的激活执行 O(1) 个操作(不包括递归调用),所以计算函数 power(x, n) 操作的总数是 O(log n) 。 在原始的时间复杂度为 O(n) 的算法上这是一个显着的改进。
在减少内存使用方面,改进版本显着节约了内存。 第一个版本的递归深度为 O(n) ,因此 O(n) 个激活记录同时被存储在内存中。 因为改进版本的递归深度是 O(log n) , 其所用内存也是 O(log n) 。
4.4.2 二路递归¶
当一个函数执行两个递归调用时,我们就说它使用了二路递归。我们已经列举了二路递归的几个例子,最具代表性的是绘制一个英式标尺(见 4 .1.2 节),或者是 4.3 节的 bad* fibonacci 函数。作为二路递归的另一个应用,让我们回顾一下计算序列 S 的 n 个元素之和问题。计算一个或零个元素的总和是微不足道的。在有两个或者更多元素的情况下,我们可以递归地计算前一半元素的总和和后一半元素的总和,然后把这两个和加在一起。在代码段 4-13 中,对于这样一个算法,实现最初是以 binary* sum(A, 0, len (A)) 而被调用的。
def binary_sum(S, start, stop):
"""Return the sum of the numbers in implicit slice S[start:stop]."""
if start >= stop: # zero elements in slice
return 0
elif start == stop-1: # one element in slice
return S[start]
else: # two or more elements in slice
mid = (start + stop) // 2
return binary_sum(S, start, mid) + binary_sum(S, mid, stop)
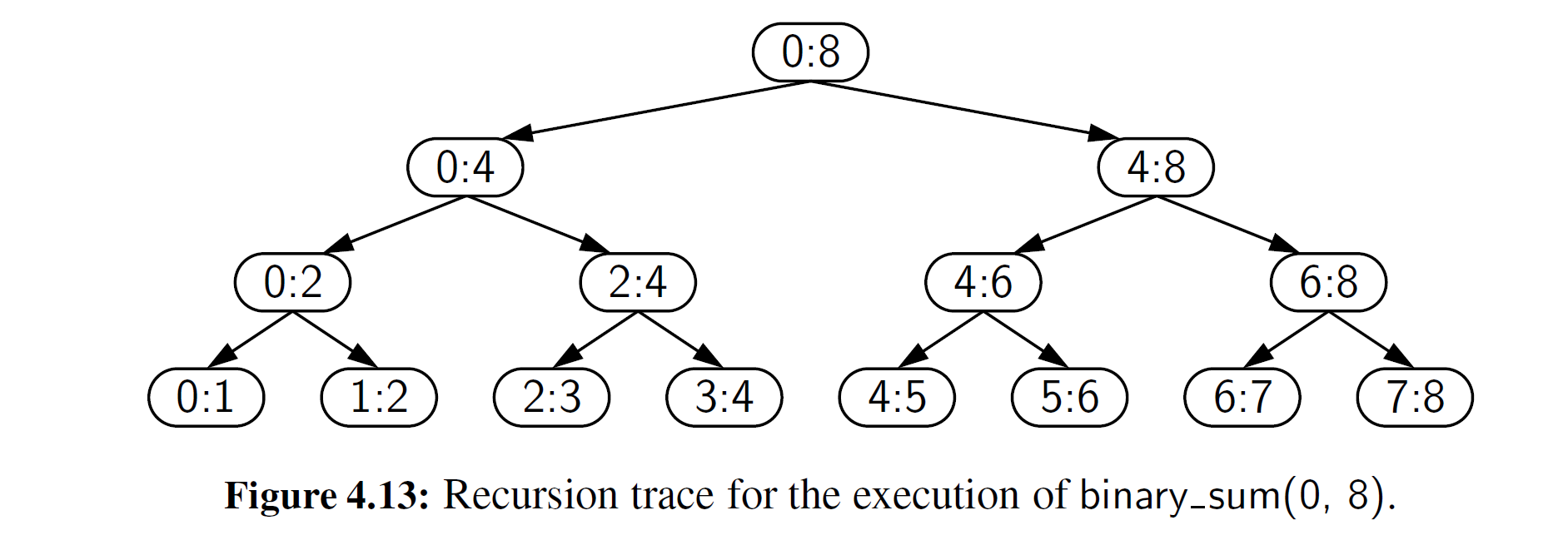
为了分析算法 binary_sum, 且为了方便起见,我们考虑当 n 为 2 的整数次幂的情况。图 4- 13 显示了 binary_sum(0, 8) 函数执行的递归追踪。我们在每个圆角矩形中添加一个标签,这个标签是所调用的参数 start : stop 的值。每次递归调用后,范围的尺寸减小一半,因 此递归的深度为 \(1 + \log_2 n\) 。因此, binary_sum 函数使用 O(log n) 数量级的额外空间.与代码段 4-9 中 linear_sum 函数使用 O(n) 数量级的空间相比,这是一个巨大的进步。然而, binary_sum 函数的时间复杂度是 O(n) , 因为有 2n - 1 函数次调用,每次都需要恒定的时间。
4.4.3 多重递归¶
从二路递归可知,我们将多重递归定义为一个过程,在这个过程中, 一个函数可能会执行多于两次的递归调用。对于一个文件系统磁盘空间使用状况分析的递归(见 4.1.4 节) 是 多重递归的一个例子,因为在一个调用期间, 递归调用执行的次数等于在文件系统给定目录 中条目的数量。
另一个多重递归的常见应用是通过枚举各种配置来解决组合谜题的情况。例如,以下是 所谓的求和谜题的所有实例:
为了解决这样的谜题,我们需要分配唯一的数字(即 0 , 1 , … , 9) 给方程中的每个字母, 以便使方程为真。 通常情况下,我们通过人工对特殊问题的观察解决这样一个谜题,这个特殊问题即解决并测试每个配置的正确性以消除配置(也就是数字与字母的可能部分分配), 直到可以得出可行的配置。
但是,如果可能配置的数量不是太大,我们可以用计算机简单地列举所有可能性,并测试每一个可能, 而不需要任何人工的观察。 此外,这种算法可以以一种系统的方式使用多重递归得出正确的配置。 代码段 4- 14 给出了这样一个算法的伪代码。 为了确保描述足以被其他问题使用,这个算法枚举并测试所有长度为 k 的序列,而且不与给定全集 \(U\) 的元素重复。
我们通过以下步骤创建含有 k 个元素的序列:
- 递归生成含有 k - 1 个元素的序列
- 附加一个元素到每个这样的未包含该元素的序列中
在算法执行的整个过程中,我们使用一个集合 \(U\) 来跟踪不包含在当前序列中的元素, 从而当且仅当元素 e 在 \(U\) 中时, 它还未被使用。
看待代码段 4-14 中算法的另一种方式是它列举 \(U\) 所有可能大小为 k 的子集, 并且测试每个子集, 这些子集是问题的可能解决方案之一。
对于求和问题, \(U = \{0, 1, 2, 3, 4, 5, 6, 7, 8, 9\}\) ,并且序列中的每个位置对应一个给定的字母。例如,第一个位置可以代表 b , 第二个位置代表 o, 第三个位置代表 y , 以此类推。
Algorithm PuzzleSolve(k,S,U):
Input: An integer k, sequence S, and set U
Output: An enumeration of all k-length extensions to S using elements in U
without repetitions
for each e in U do
Add e to the end of S
Remove e from U {e is now being used}
if k == 1 then
Test whether S is a configuration that solves the puzzle
if S solves the puzzle then
return “Solution found: ” S
else
PuzzleSolve(k−1,S,U) {a recursive call}
Remove e from the end of S
Add e back to U {e is now considered as unused}
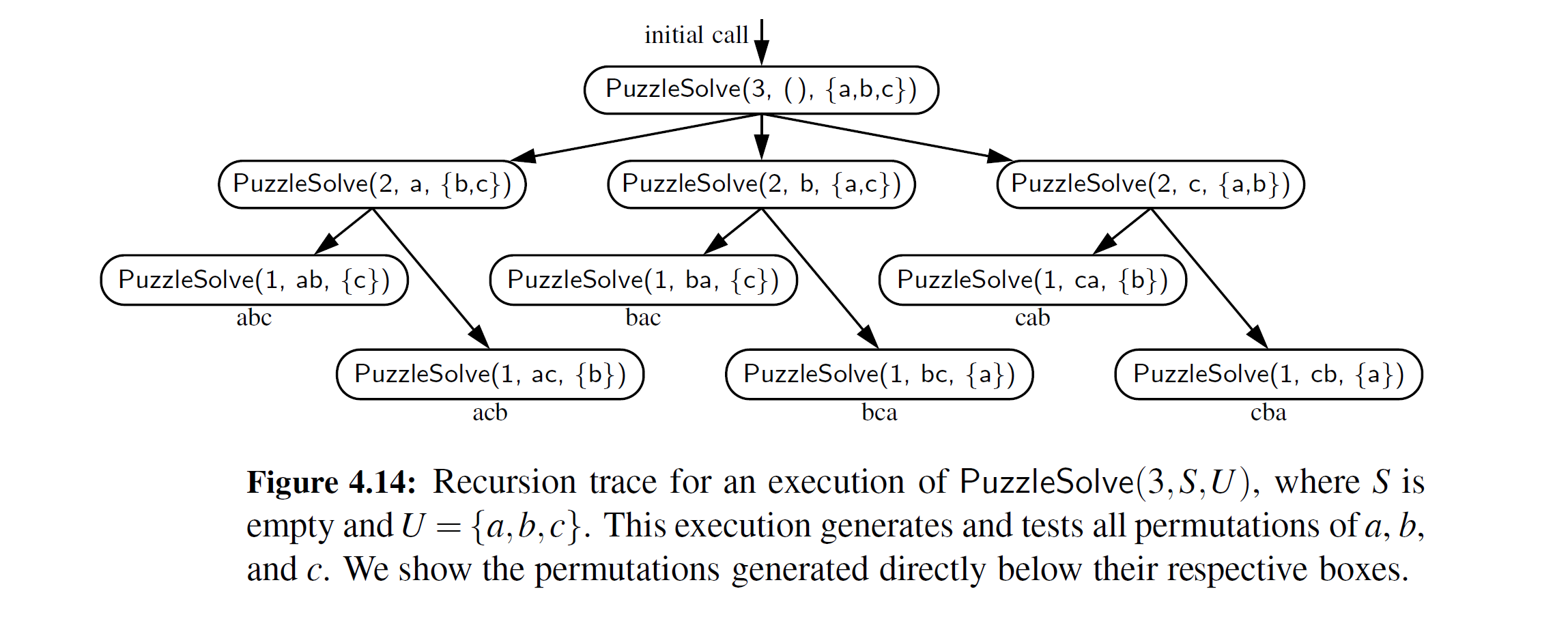
图 4-14 显示了 PuzzlSolve(3, S , U) 函数调用的递归追踪,其中 S 为空并且 U = {a, b, c} 。这个执行生成并测试了 a, b, c 三个字符的所有排列。注意初始调用进行三次递归调用,其中每一个调用又进行两次甚至更多次调用。在一个包含四个元素的集合 U 上, 如果已经执行 了 PuzzleSolve(3, S, U) ,那么初始调用可能已经进行了四项递归调用,其中每一个调用将有一个追踪——类似于图 4-14 描述的一样
4.5 设计递归算法¶
一般来说,使用递归的算法通常具有以下形式:
- 对于基本情况的测试。首先测试一组基本情况(至少应该有一个) 。这些基本情况应该被定义,以便每个可能的递归调用链最终会达到一种基本情况,并且每个基本情况的处理不应使用递归。
- 递归。如果不是一种基本情况, 则执行一个或多个递归调用。这个递归步骤可能包括一个测试,该测试决定执行哪几种可能的递归调用。我们应该定义每个可能的递归调用,以便使调用向一种基本情况靠近。
参数化递归¶
要为一个给定的问题设计递归算法,考虑我们可以定义的子问题的不同方式是非常有用的,该子问题与原始问题有相同的总体结构。如果很难找到需要设计递归算法的重复结构, 解决一些具体问题有时是有用的,这样可以看出子问题应该如何定义。
一个成功的递归设计有时需要重新定义原来的问题,以便找到看起来相似的子问题。这通常涉及参数化函数的特征码。例如,在一个序列中执行二分查找算法时,对调用者的自然函数特征码将显示为 binary_search(data, target) 。不过,在 4.1.3 节中,我们调用特征码 binary_search(data, target, low, high) 定义函数,并且使用额外的参数说明子列表作为递归过程。对于二分查找来说, 在参数化方面的这个改变是至关重要的。如果坚持简便的特征值 binary_search(data, target) , 在列表的一半进行搜索的唯一方法可能是建立一个只含有这些元素的新列表并且把它作为第一个参数。然而,复制列表的一半已经需要 O(n) 的时间,这就否定了二分查找算法全部的优点。
如果希望给一个像二分查找这样的算法提供一个简洁的公共接口,而不会干扰用户的其他参数, 那么标准的技术是创建一个有简洁接口的公共函数,比如 binary_search(data, target) , 然后让它的函数体调用一个非公共的效用函数,这个效用函数含有我们所希望的递归参数。
你会发现我们对本章其他几个例子的递归类似地进行了重新参数化( 例如, reverse 、linear_sum 及 binary_sum ) 。在 good_fibonacci 函数的实现中,通过有意加强返回的期望(在这种情况下,返回的是一对数字而不是一个数字) ,我们看到了一种用以重新定义递归的不同方法。
4.6 消除尾递归¶
算法设计的递归方法的主要优点是,它使我们能够简洁地利用重复结构呈现诸多问题。通过使算法描述以递归的方式利用重复结构, 我们经常可以避开复杂的案例分析和嵌套循环。这种方法会得出可读性更强的算法描述,而且十分有效。
然而,递归的可用性要基于合适的成本。特别是, pythontbon 解释器必须保持跟踪每个嵌套调用的状态的活动记录。当计算机内存价格昂贵时,在某些情况下,能够从那些递归算法得到非递归算法是很有用的。
在一般情况下,我们可以使用堆栈数据结构,堆栈结构将在 6.1 节介绍,通过管理递归,结构自身的嵌套,而不是依赖于解释器,从而把递归算法转换成非递归算法。虽然这只是把内存使用从解释器变换到堆栈,但是也许能够通过只存储最小限度的必要信息来减少内存使用。
更好的情况是,递归的某些形式可以在不使用任何辅助存储空间的情况下被消除。其中一种著名的形式被称为尾递归(tail recursion ) 。如果执行的任何递归调用是在这种情况下的最后操作,而且通过封闭递归,递归调用的返回值( 如果有的话)立即返回,那么这个递归是一个尾递归。根据需要, 一个尾递归必须是线性递归(因为如果必须立即返回第一个递归调用的结果,那么将无法进行第二次递归调用) 。
在本章给出的递归函数中,代码段 4-3 的 binary_search 函数和代码段 4-10 的 reverse 函数均是尾递归的例子。虽然其他几个线性递归很像尾递归,但技术上并不是如此。例如,代 码段 4 - 1 中的阶乘函数不是一个尾递归。它最后的命令:
return n * factorial(n - 1)
这不是一个尾递归,因为递归调用完成之后进行了额外的乘法运算。出于类似的原因,代码段 4-9 的 linear_sum 函数和代码段 4-7 的good_fibonacci 函数也不是尾递归
在重复循环中,通过封闭函数体, 并且通过重新分配现存参数的这些值以及用新的参数来代替一个递归调用,任何尾递归都可以被非递归地重新实现。举一个实例,如代码段 4- 15 所示, binary_search 函数可以被重新实现,仅需要在 while 循环之前, 初始化变量 low 和 high 来表示序列的完整的程度。然后,经过每次的循环找到目标值或者缩小候选子序列的范围。
def binary_search_iterative(data, target):
"""Return True if target is found in the given python list."""
low = 0
high = len(data)-1
while low <= high:
mid = (low + high) // 2
if target == data[mid]: # found a match
return True
elif target < data[mid]:
high = mid - 1 # only consider values left of mid
else:
low = mid + 1 # only consider values right of mid
return False # loop ended without success
在最初版本中进行递归调用 binary_search(data, target, low, mid - 1) 函数的地方,仅用 high = mid - 1 进行替换,然后继续下一个循环的迭代。最初的基本情况的条件 low > high 只被相反的循环条件 while low <= high 所取代。在新的实现中,如果 while 循环结束,则用返回 False 来特指查找失败(也就是说,没有从内部返回 True) 。
我们同样可以实现代码段 4-10 原始递归逆置( reverse ) 方法的非递归实现,如代码段 4-16 所示。
def reverse_iterative(S):
"""Reverse elements in sequence S."""
start, stop = 0, len(S)
while start < stop - 1:
S[start], S[stop-1] = S[stop-1], S[start] # swap first and last
start, stop = start + 1, stop - 1 # narrow the range
在新版本中,在每个循环期间,更新 start 和 stop 的值。一旦在这个范围内只有一个或者更少的元素,即退出。
即使许多其他线性递归不是正式的尾递归,它们也可以非常有效地用迭代来表达。例 如,对于计算阶乘、求序列元素的和或者有效地计算斐波纳契数,都有简单的非递归实现。事实上,从 1. 8 节可以看出, 斐波那契数生成器的实现使用 O(1) 的时间产生每个子序列的 值,因此需要 O(n) 的时间来产生该系列中的第 n 个条目。
对双路递归的理解:汉诺塔问题¶
汉诺塔(Tower of Hanoi)是根据一个传说形成的数学问题:
有三根杆子 A,B,C。A 杆上有 N 个 (N>1) 穿孔圆盘,盘的尺寸由下到上依次变小。要求按下列规则将所有圆盘移至 B 杆:
-
每次只能移动一个圆盘;
-
大盘不能叠在小盘上面。
提示:可将圆盘临时置于 C 杆,也可将从 A 杆移出的圆盘重新移回 A 杆,但都必须遵循上述两条规则。
问:如何移?最少要移动多少次?
要完成这个问题,不应该直接考虑一般情况下(即 n 个圆盘时的情况)如何移动圆盘,这会使问题变得无比复杂——在我们这一章——递归的主题下,我们应该首先考虑基本情况——仅有一个圆盘的情况(记较小者为 1,较大者为 2,其他情况则类似,如对于标记 1、2、3 而言,圆盘 1 小于圆盘 2,圆盘 2 则小于圆盘 3)
- 将 1 移动至 b
接着考虑需要进行一次递归的情况
- 将 1 移动至 c
- 将 2 移动至 b
- 将 1 移动至 b
因此整个递归的流程是
- 先将(n - 1)个盘子移动到 c
- 将第 n 个盘子移动到 b
- 将(n - 1)个盘子移动到 b
要注意的是,在得出这个算法的过程中,我们并未考虑我们应该按照如何的顺序来挪动这(n - 1)个盘子,因此显然这是一个二路递归
def hanoi(n, a, b, c):
if n == 1:
print(a, '-->', b)
else:
hanoi(n - 1, a, b, c)
hanoi(1 , a, c, b)
hanoi(n - 1, c, a, b)
# 调用
if __name__ == '__main__':
hanoi(5, 'A', 'B', 'C')
从而我们能够在不知道具体如何移动的情况下得出具体需要几步才能完成这一谜题——\(2^n-1\) 次(基于对基本情况的调用次数,或者说,该递归函数的调用次数)
小结¶
递归算法的精髓在于——虽然我们在编写程序时是以自上而下的顺序(即 n → 1)来调用递归函数,但在实际执行程序时,计算机会以自下而上的顺序(即 1 → n)来进行计算——这就是说计算机是以基本情况出发来得到最终的结果的
这也为我们在设计算法时提供了巨大的便利——我们不需要直接考虑在某种可能十分复杂的适用于一般情况的算法,而是反过来,从一个比较简单的基本情况出发,通过对基本情况的不断重复来完善算法。上面的汉诺塔问题就是一个比较好的例子,直接考虑如何移动盘子这个十分细节并且具有一般性的问题十分复杂,但从基本情况出发,通过不断调用递归函数,我们就能在不求甚解的情况下得到整个过程
另一个例子是二分法查找数字,该递归的基本情况其实并不需要 mid 这一参数。我们可以如此描述这一算法的大致轮廓:
- 算法的目的是要找到某一个值 \(n\),那么如果我们可以使用某种方法使我们的搜索区间最终限定在区间 \([n,n]\) 上,那么也就相当于完成了算法的任务,从而我们得到了该递归算法的基本情况:区间 \([n,n]\)
- 接下来的问题就比较简单,如何让搜索区间在不断变小的同时不断趋向区间 \([n,n]\) 变化?事实上,想怎么分都可以,不过二分可以证明是期望用时最短的方法(见概率论),最终我们使得搜索区间变为区间 \([n,n]\)
从上面的思路中我们也可以看出来尾递归和一般递归之间的不同之处:通俗的讲,尾递归无论调用了几次递归函数,基本情况只执行了一次(比如对一般的二路递归来说,基本情况会被实现 \(2^n\) 次),这也是尾递归仅能出现在线性递归中的原因——虽然某些二路或者多路递归也仅仅返回了一个值,但是基本情况执行了许多次——用一种不太准确的话来说,对于一种尾递归算法而言,其在一次运行过程所调用的所有递归函数都是同一个值,即对应的基本情况——这也是阶乘算法不属于尾递归的原因,其在一次运行中每次调用的递归函数的值不一样:这是因为其每次递归调用返回的值都要乘上 n
再举一个例子:使用二分法来计算一个序列中所包含的值,其实二分法不是重点,重点是基本情况——\(a +b\)——它是构成递归这个分型的一个小元素;换句话说,整个序列中的元素之和其实是许多这样的基本情况之和,而二分法仅仅只是我们得到基本情况的手段
- 需要注意的是,所谓的基本情况并非是可以随便定义的,其应该是符合算法目的的最简情况——比如在求和算法中,它是符合求和这一目的的最简单的情况 \(a+b\) 而非 \(a+b+c\),即该基本情况必须“相似”于整体