第 6 章 栈、队列和双端队列

6.1 栈

栈是由一系列对象组成的一个集合，这些对象的插入和删除操作遵循==后进先出 ( LIFO )== 的原则。用户可以在任何时刻向栈中插入一个对象｀ 但只能取得或者删除最后一个插入的对象（即所谓的＂栈顶＂) 。 "栈” 这个名字来源于自动售货机中用弹簧顶住的一堆盘子的隐喻。在这种情况下，其基本的操作只涉及向这个栈中取盘子或者放盘子。当需要从 这个自动售货机中取一个新盘子时，我们 ” 取 “ 出这个栈顶的盘子。当需要向其中添加一个盘子的时候， 我们将盘子＂压＂入栈顶， 使其成为新的栈顶。或许一个更加有趣的例子是 PEZ 糖果售卖器，当售卖器的顶部打开时， 它将存储在容器里面的糖果从顶部逐个弹出， 如图 6 - 1 所示。栈是一个基本的数据结构。很多应用程序都会用到栈，下面是一些使用堆栈的示例。

例题 6-1 : 网络浏览器将最近浏览的网址存放在一个栈中。每次当访问者访问一个新网站时，这个新网站的网址就被压入栈顶。这样， 浏览器就可以在用户单击 “后退” 按钮时，弹出先前访问的网址，以回到其先前访问的 网页。

例题 6-2: 文本编辑器通常提供一个 “撤销“ 机制以取消最近的编辑操作并返回到先前的文本状态。这个撤销操作就是通过将文本的变化状态保存在一个栈中得以实现的。

6.1.1 栈的抽象数据类型

栈是最简单的数据结构，但它同样也是最重要的数据结构。它们被用在一系列不同的应用中，并且在许多更加复杂的数据结构和算法中充当工具。从形式上而言，栈是一种支待以下两种操作的抽象数据类型( ADT ) ，用 S 表示这一 ADT 实例：

• S.push(e) ： 将一个元素 e 添加到栈 S 的栈顶。
• S.pop(e) ：从栈 S 中移除并且返回栈顶的元素， 如果此时栈是空的，这个操作将出错。

此外，为了方便， 我们定义了以下访问方法：

• S.top() ： 在不移除栈顶元素的前提下，返回一个栈 S 的栈顶元素；若栈为空，这个操作会出错。
• S. is_empty()： 如果栈中不包含任何元素， 则返回一个布尔值 " True " 。
• len(S) ：返回栈 S 中元素的数量；在 python 中，我们用__len__这个特殊的方法实现它。

按照惯例，我们假定一个新创建的栈是空的，并且其容量也没有预先的限制。添加进栈的元素可以是任何类型的。

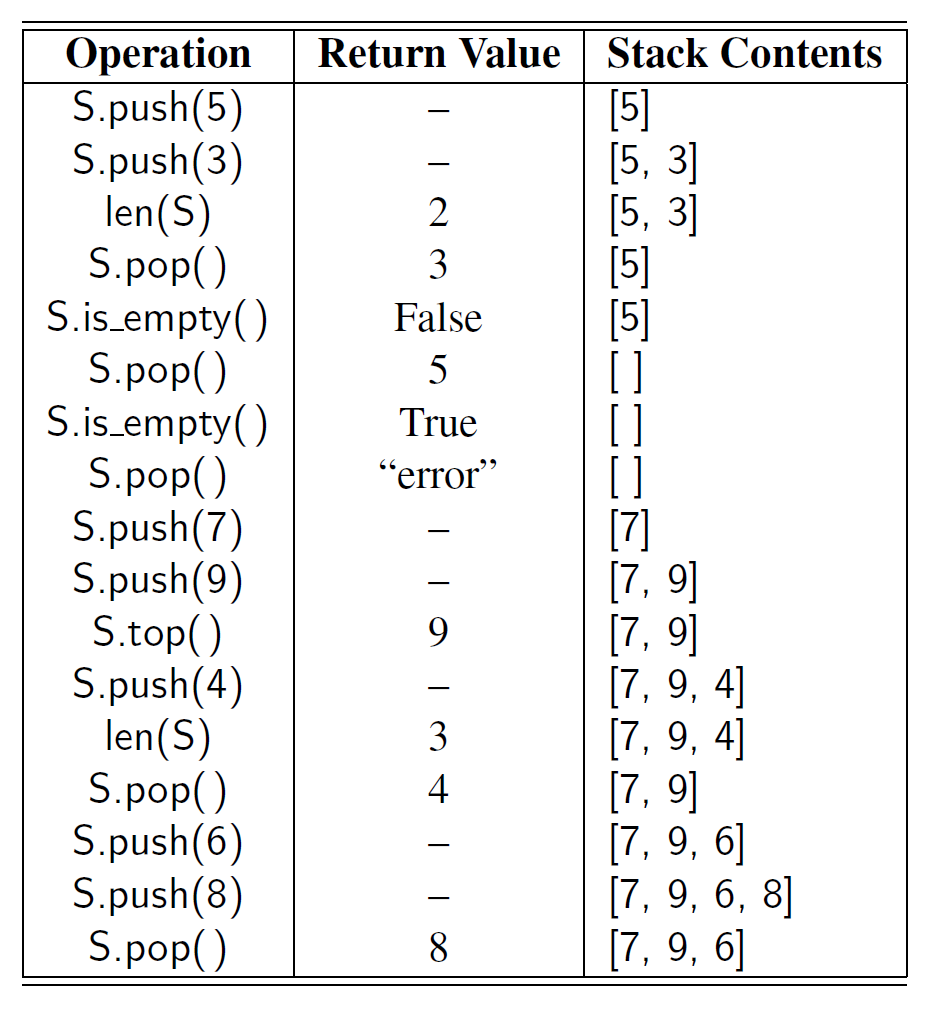
例题 6-3: 下表展示了在一个初始化为整数类型的空栈 S 中进行一系列操作的结果。

6.1.2 简单的基于数组的栈实现

我们可以简单地通过在 python 列表中存储一些元素来实现一个栈。list 类已支持 append 方法，用于添加一个元素到列表尾部，并且支 持 pop 方法，用于移除列表中最后的元素，所以我们可以很自然地将一个列表的尾部与一个栈的顶部相对应起来，如图 6-2 所示。

虽然程序员可以直接用 list 类代替一个正式的 stack 类，但是列表还包括一些不符合这种抽象数据类型的方法（比如： 增加或者移除处于列表任何位置的元素） 。同时， list 类所使用的术语也不能与栈这种抽象数据类型的传统命名方法精确对应，特别是 append 方法和 push 方法之间的区别。相反，我们将强调如何使用一个列表实现栈元素的内部存储，并同时提供一个符合堆栈的公共接口。

适配器模式

适配器设计模式适用于任何上下文，从而使我们可以有效地修改一个现有的类，以使它的方法能够与那些与其相关但又不同的类或接口相匹配。一个应用这种适配器模式的通用方法是以这样一种方式定义一个新类，这种方式以包含一个现存类的实例作为隐藏域，然后用这个隐藏实例变拯的方法实现这个新类的方法。以这种方式应用适配器模式，我们已经创建了一个新类，它可以执行一些与现有类相同的函数功能，却以一种更加方便的方式重新封 装。对于栈这种抽象数据类型结构，我们可以通过改编 python 的 list 类中相应的内容来实现，见表 6-1 。

用 python 的 list 类实现一个栈

我们用适配器设计模式定义了一个 ArrayStack 类，并且使用一个基本的 python 列表进行存储（之所以选择这个 ArrayStack 名字，是为了强调底层的存储是基于数组的） 。现在还有一个问题，那就是当这个栈是空的时候，如果一个用户调用 pop 或者 top 方法时，代码应 该怎样处理。ADT 给出的建议是触发一个错误，但是必须要决定这是一个什么类型的错误。

当在一个空的 python 列表中调用 pop 方法时，正常情况下会触发一个 IndexError （请求的索引超出序列范围），因为列表是基于索引的序列。对于栈而言， 这个选择似乎并不恰当， 因 为这里并没有假定的索引。其实，定义一个新的异常类更为恰当。代码段 6-1 定义了这样一 个 Empty 类作为 python Exception 类的一个小的子类。

class Empty(Exception):
  """ Error attempting to access an element from an empty container."""
  pass

我们在代码段 6-2 中给出了 ArrayStack 类的正式定义。由于是内部存储，因此构造函数建立 self._data 数据成员作为一个初始化的空 python 列表。余下的公共栈方法将根据表 6-1 中对应的方法实现。

使用实例

下面展示了 ArrayStack 类的一个使用实例，映射了例题 6-3 一开始列出的操作。

from ..exceptions import Empty

class ArrayStack:
  """LIFO Stack implementation using a python list as underlying storage."""

  def __init__(self):
    """Create an empty stack."""
    self._data = []                       # nonpublic list instance

  def __len__(self):
    """Return the number of elements in the stack."""
    return len(self._data)

  def is_empty(self):
    """Return True if the stack is empty."""
    return len(self._data) == 0

  def push(self, e):
    """Add element e to the top of the stack."""
    self._data.append(e)                  # new item stored at end of list

  def top(self):
    """Return (but do not remove) the element at the top of the stack.

    Raise Empty exception if the stack is empty.
    """
    if self.is_empty():
      raise Empty('Stack is empty')
    return self._data[-1]                 # the last item in the list

  def pop(self):
    """Remove and return the element from the top of the stack (i.e., LIFO).

    Raise Empty exception if the stack is empty.
    """
    if self.is_empty():
      raise Empty('Stack is empty')
    return self._data.pop()               # remove last item from list

分析基于数组的栈的实现

表 6-2 展示了 Array Stack 方法的运行时间。这个分析直接与 5.3 节给出的 list 类的分析相对应。在最坏的情况下， top 、is_empty 和 len 方法均在常量时间内完成。对于 push 和 pop 操作的时间复杂度为 O(1) ， 指的是均摊计算的边界（参见 5.3.2 节）；对于这些方法中任何一个典型的调用都仅需要常量的时间， 但是当一个操作导致了列表重新调整其内部数组的大小时，偶尔在最坏的情况下也会要 O(n) 的时间开销，其中 n 是当前栈中元素的个数。对于栈的空间利用率是 O(n) 。

避免由于预留空间所导致的摊销

在某些情况下，会有额外的知识表明一个栈将会达到最大的尺寸。从代码段 6-2 看， ArrayStack 的实现开始于一个空的列表并且随着需要对它进行扩展。根据 5.4.1 节对列表的分析， 我们相信，在实际中构造一个最初长度为 n 的列表要比一开始就从一个空的列表开始逐步添加 n 项更加有效（即使两种方法均能在 O(n) 时间内运行完毕） 。

作为一个栈的替代模型，我们可能希望构造函数接受一个用于指定一个堆栈的最大容量的参数并且初始化数据成员列表的长度。实现这样一个模型需要对代码段 6-2 做出大量改写。栈的长度将不再是列表的长度的同义词，并且对栈的 push 和 pop 操作也不再需要改变列表的长度。相反，我们建议单独维护一个整数作为实例变量以表示当前栈中元素的个数。这个实现过程的细节在课后练习 C-6.17 中展开讨论。

6.1.3 使用栈实现数据的逆置

由于 LIFO 协议，栈可以用作一种通用的工具，用于实现一个数据序列的逆置。例如， 如果值 1 、2 、3 被顺序压入一个栈中，它们将会以 3 、2 、1 的顺序被逐个弹出。

这一思想可以被应用在各种设置中。例如，我们希望逆序打印一个文件的各行，目的是以降序（而非升序）的方式显示一个数据集。我们可以通过先逐行读出数据，然后压入一个栈中，再按照从栈中弹出的顺序来写入。这个方法的实现过程在代码段 6-3 中给出。

def reverse_file(filename):
  """Overwrite given file with its contents line-by-line reversed."""
  S = ArrayStack()
  original = open(filename)
  for line in original:
    S.push(line.rstrip('\n'))     # we will re-insert newlines when writing
  original.close()

  # now we overwrite with contents in LIFO order
  output = open(filename, 'w')    # reopening file overwrites original
  while not S.is_empty():
    output.write(S.pop() + '\n')  # re-insert newline characters
  output.close()

一个值得注意的技术细节是我们在读取时故意将行中的换行符去掉，然后在写入结果文 件时重新在每一行中插入换行符。之所以这样做，是为了处理一种特殊的情况，这种特殊情 是在原始文件的最后一行并没有换行符。如果我们只是完全逆置地输出从文件中读取的每 一行，那么这个原始文件的最后一行后面将紧跟着倒数第二行而没有新的换行符。我们的实现方法确保了结果中有分离换行符。

使用一个栈来实现数据集的逆置的思想也可以应用在其他类型的序列。例如，练习 R-6.5 就尝试使用栈来实现 python 列表内容逆置的另一个解决方案(4.4.1 节中讨论了一个 递归的解决方案） 。一个更具有挑战性的任务是如何将存储在一个栈中的元素逆置。如果将它们从一个栈移到另一个栈中，那么它们将会被逆置，但是如果再次将它们放回原来的栈， 那么它们将会再次被逆置，即又回到了最初的顺序。练习 C-6.18 对这个任务的解决方案进行了探索。

6.1.4 括号和 HTML 标记匹配

在本节中，我们将探索两个栈的相关应用，这两个应用都涉及对一串匹配分隔符的测试。在第一个应用中，我们设想算数表达式可能包含几组不同的成对符号，如：

• 括号：“（ ” 和 “ ）”
• 大括号：“ { ” 和 “ } ”
• 方括号：“ [ ” 和 “ ] ”

每个开始符号必须与其对应的结束符号相匹配。 例如，左括号 “ [ ” 必须匹配相应的右括号 “ ] ”，如表达式 [(5+x)-(y+z)] 中所示。 下面的例子进一步说明了这个概念：

• 正确的：（）（（ ））{（[（ ）]）}
• 正确：((( )(( )){([( )])}))
• 不正确：)(( )){([( )])}
• 不正确：({[ ])}
• 不正确：(

我们将匹配符号组的精确定义留给练习 R-6.6

分隔符的匹配算法

在处理算术运算表达式时的一个重要任务是确保表达式中的分隔符匹配正确。代码段 6-4 给出了一个用 python 实现这一功能的算法。

def is_matched(expr):
  """Return True if all delimiters are properly match; False otherwise."""
  lefty = '({['                               # opening delimiters
  righty = ')}]'                              # respective closing delims
  S = ArrayStack()
  for c in expr:
    if c in lefty:
      S.push(c)                               # push left delimiter on stack
    elif c in righty:
      if S.is_empty():
        return False                          # nothing to match with
      if righty.index(c) != lefty.index(S.pop()):
        return False                          # mismatched
  return S.is_empty()                         # were all symbols matched?

假定输入的是字符序列如 [(5 + x) - (y + z)］，对原始的序列从左到右进行扫描，使用栈匹配这一组分隔符。每次遇到开始符时，我们都将其压入栈中；每次遇到结束符时，我们从栈顶弹出一个分隔符（假定栈不为空），并检查这两个分隔符是否能够组成有效的一对。如果扫描到表达式的最后并且栈为空，则表明原来的算数表达式匹配正确； 否则，栈中一定存在一个开始分隔符没有被匹配。

如果原始算数表达式的长度为 n, 这个算法将最多 n 次调用 push 和 n 次调用 pop 。即使假设这些询用的均摊复杂度边界 O(1) ，这些调用总运行时间仍为 O(n) 。对于给定的可能出 现的分隔符（｛［，其大小为常量，追加测试如 lefty 中的 c 和 righty.index(c) ， 其实际运行时间都在 O(1) 之内。结合这些操作，一个序列长度为 n 的匹配算法的运行时间为 O(n) 。

标记语言的标签匹配

另一个分隔符匹配应用是在标记语言（如 HTML 或 XML) 的验证中。HTML 是互联网上超文本文档的标准格式， XML 是用于各种数据集的扩展标记语言。图 6-3 所示即为一个 HTML 文件实例和一个可能的对应的翻译

在一个 HTML 文本中，部分文本是由 HTML 标签分隔的。一个简单的 HTML 开始标 签的形式为 " " ，相应的结束标签的则是" " 的形式。例如，我们在图 6-3a 的第一行中看到了标签 ，并在末尾看到了与其相匹配的标签 。在这个例子 中，其他一些经常使用的 HTML 标签如下：

• body : 文档内容
• hl: 节标题
• center: 居中对齐
• p: 段落
• ol: 编号（命令）列表
• Ii：表项

理想情况下， 一个 HTML 文本应该有相匹配的标记，尽管大多数浏览器能够容忍一定数量的失配标签。代码段 6-5 给出了一个 python 函数，这个函数实现在一个代表 HTML 文 本的字符串中进行标签匹配。我们从左往右扫描原始字符串，用符号 j 来跟踪我们的进度， 并且用 str 类的 find 方法来定位定义了这个标签的 " " 字符。开始标签被压入栈中， 当其从栈中弹出时，即与结束标签进行匹配。正如我们在代码段 6-4 中匹配分隔符所做的那 样。通过相似的分析，这个算法的运行时间为 O(n) ，其中 n 是这个原始 HTML 文本中字符的数量。

def is_matched_html(raw):
  """Return True if all HTML tags are properly match; False otherwise."""
  S = ArrayStack()
  j = raw.find('<')               # find first '<' character (if any)
  while j != -1:
    k = raw.find('>', j+1)        # find next '>' character
    if k == -1:
      return False                # invalid tag
    tag = raw[j+1:k]              # strip away < >
    if not tag.startswith('/'):   # this is opening tag
      S.push(tag)
    else:                         # this is closing tag
      if S.is_empty():
        return False              # nothing to match with
      if tag[1:] != S.pop():
        return False              # mismatched delimiter
    j = raw.find('<', k+1)        # find next '<' character (if any)
  return S.is_empty()             # were all opening tags matched?

6.2 队列

队列是另一种基本的数据结构，它与栈互为 ”表亲“ 关系，队列是由一系列对象组成的集合，这些对象的插入和删除遵循先进先出(F irst in First out, FIFO) 的原则。也就是说， 元素可以在任何时刻进行插入，但是只有处在队列最前面的元素才能被删除。

我们通常将队列中允许插入的一端称为队尾， 将允许删除的一端则称为队头。对这个术语的一个形象比喻就是一队人在排队进入游乐场。人们从队尾插入排队等待进入游乐场，而 从这个队的队头进入游乐场。还有许多其他关于队列的应用，如图 6-4 所示。商店、影院 预订中心和其他类似的服务场所通常按照 “先进先出” 的原则处理客户的请求。对于顾客服务中心的电话呼叫或者餐厅的等候顾客而言，队列会成为一个合乎逻辑的选择。FIFO 队列还广泛应用于许多计算设备中，比如一个网络打印机或者一个响应请求的 Web 服务器。

6.2.1 队列的抽象数据类型

通常来说，队列的抽象数据类型定义了一个包含一系列对象的集合，其中元素的访问和删除被限制在队列的笫一个元素，而且元素的插入被限制在序列的尾部。这个限制根据先进先出原则执行元素的插入和删除操作。对于队列 Q 而言，队列的抽象数据类型( ADT ) 支持 如下两个基本方法：

• Q.enqueue(e) ：向队列 Q 的队尾添加一个元素。
• Q.dequeue() ：从队列 Q 中移除并返回第一个元素，如果队列为空，则触发一个错误。

队列的抽象数据类型 (ADT) 还包括如下方法（第一个类似于堆栈的 pop 方法） ：

• Q.first()：在不移除的前提下返回队列的第一个元素；如果队列为空，则触发一个错误。
• Q.is_empty()：如果队列 Q 没有包含任何元素则返回布尔值 ” True” 。
• len(Q) ：返回队列 Q 中元素的数量；在 python 中，我们通过＿＿len_＿这个特殊的方 法实现。

按照惯例，假设一个新创建的队列为空，并且队列的容量没有先天的上限。添加进去的元素也没有任何类型限制。

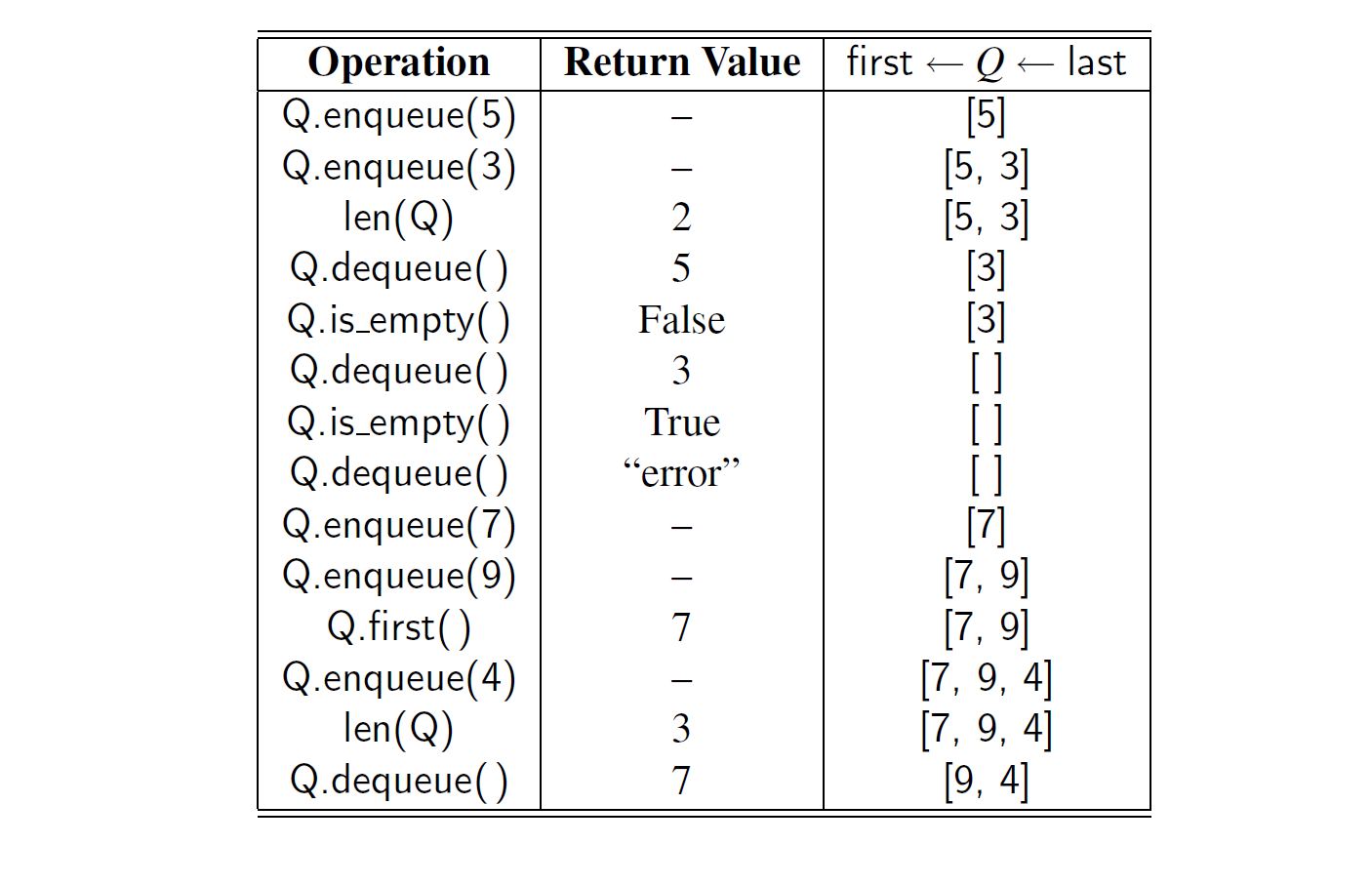
例题 6-4: 下表列出了一系列队列的操作和在最初为空的整数类型队列中实施这些操作后的效果。

6.2.2 基于数组的队列实现

对于栈这种抽象数据结构类型，我们用 python 列表作为底层存储创造了一个非常简单的适配器类，也可以使用类似的方法支持一个队列的抽象数据类型。我们可以通过调用 append(e) 方法将 e 加至列表的尾部。当一个元素退出队列时，我们可以使用 pop(0) 而不是 pop()从列表中来有意移除第一个元素。

由于这个实现很容易，因此它也最为低效。正如我们在 5.4.1 节讨论的，当 pop 操作在 一个列表中以非索引的方式调用时，可以通过执行一个循环将所有在特定索引另一边的元素转移到它的左边，目的是为了填补由 pop 操作给序列造成的“洞” 。因此， 一个 pop(0) 操作 的调用总是处于最坏的情况，耗时为 Θ(n) 。

我们可以改进上面的策略，完全避免调用 pop(0) 。可以用一个指代为空的指针代替这个数组中离队的元素，并且保留一个显式的变量 f 来存储当前在最前面的元素的索引。这样一 个算法对于离队操作而言耗时为 O(1) 。几次离队操作后，这个方法可能会导致如图 6-5 所示的情景。

不幸的是，修改后的方法仍然有一个缺点。在一个栈的设计中，列表的长度就是栈的大小（甚至列表底层的存储数组略大） 。对于我们 正在考虑的队列的设计，情况更糟。例如，建立一个含有相对较少元素的队列时，系统可能让这些元素存储在一个任意大的列表中。如果不断重复地往一个队列中添加一个新的元素， 然后删除另一个（允许最前端向右漂移），就会发生这样的清况，即随着时间的推移，底层列表的大小将逐渐增长到 O(m) ，其中 m 值等于自队列创建以来对队列进行追加元素操作的数量总和，而不是当前队列中元素的数量

这种设计会在一些所需队列的大小相对稳定却被长时间使用的应用程序中产生不利的影响。例如，餐厅点餐队列的长度在某一个时刻基本上不可能超过 30 个，但是在一天（或者一周）， 排队的总长度将非常大

循环使用数组

为了开发一种更加健壮的队列实现方法，我们让队列的前端趋向右端，并且让队列内的元素在底层数组的尾部 “ 循环＂ 。假定底层数组的长度为固定值 N, 它比实际队列中元素的数量大。新的元素在当前队列的尾部利用入队列操作进入队列，逐步将排在队列前面的元素从队列的前面插入索引为 N - 1 的位置，然后紧接着是索引为 0 的位置，接下来是索引为 1 的位置。图 6-6 所示为一个第一个元素为 E 最后一个元素为 M 的队列，可用于说明这一过程。

实现这种循环的方法并不困难。当从队列中删除一个元素并欲更新前面的索引时，我们可以使用算式 \(f=(f+ 1)\%N\) 进行计算。回想一下在 python 中 ％ 操作指的是 “模” 运算操作，它是整数除法之后取余数的值。例如， 14 被 3 整除得到的商为 4 余数为 2, 即 \(\frac{14}4=4\frac23\)。因 此， 在 python 中， 14 // 3 得到的结果为 4, 而 14 % 3 的结果为 2 。取模操作是处理一个循环数组的理想操作。举一个具体的例子，如果有一个长度为 10 的列表，并且一个索引为 7 的首部，我们可以通过计算 (7 + 1)%10 来更新首部，这很简单地就计算出是 8, 因为 8 除以 10 商为 0, 余数是 8 。同样，更新索引为 8 后将会进入索引为 9 的单元。但是当从索引为 9 （数组的最后一个单元）处更新时，需要计算 (9 + 1)%10, 其结果为得到索引为 0 的位置（因为 10 被 10 整除，余数为 0)

python 队列的实现方法

在代码段 6-6 和代码段 6-7 中，我们给出了通过使用 python 列表以循环的方式来实现 一个队列的抽象数据类型的完整方法。其中，这个队列类维护如下 3 个实例变量：

• _data: 指一个固定容量的列表实例。
• _size :是一个整数，代表当前存储在队列内的元素的数量（与＿data 列表的长度正好相对） 。
• _front ：是一个整数，代表＿data 实例队列中第一个元素的索引（假定这个队列不为空） 。

尽管这个队列的大小通常为 0, 但我们还是初始化一个可以保存中等大小的列表用于存储数据。同时，我们还将这个队列＿front 索引初始化为 0 。

当队列为空， front 或者 dequeue 操作被调用时，系统会抛出一个 Empty 异常实例， 在代码段 6-1 中，我们为栈定义了这个异常操作。

注：不要先入为主的认为基于数组定义的队列其头部一定位于数组的 0 索引处，这会对理解造成很大障碍，基于鸭子方法，我们使用数组所构造的队列类只要满足 FIFO 协议即可（即先出后进），而不是拘泥于队伍的头部在数组的哪个位置，数组只是实现队列的一个手段

• 在几次队伍的进出后，后面进入队伍的元素可能甚至排在（在数组内位置的意义上）队伍头部的前面

from ..exceptions import Empty

class ArrayQueue:
  """FIFO queue implementation using a python list as underlying storage."""
  DEFAULT_CAPACITY = 10          # moderate capacity for all new queues

  def __init__(self):
    """Create an empty queue."""
    self._data = [None] * ArrayQueue.DEFAULT_CAPACITY
    self._size = 0
    self._front = 0

  def __len__(self):
    """Return the number of elements in the queue."""
    return self._size

  def is_empty(self):
    """Return True if the queue is empty."""
    return self._size == 0

  def first(self):
    """Return (but do not remove) the element at the front of the queue.

    Raise Empty exception if the queue is empty.
    """
    if self.is_empty():
      raise Empty('Queue is empty')
    return self._data[self._front]

  def dequeue(self):
    """Remove and return the first element of the queue (i.e., FIFO).

    Raise Empty exception if the queue is empty.
    """
    if self.is_empty():
      raise Empty('Queue is empty')
    answer = self._data[self._front]
    self._data[self._front] = None         # help garbage collection使头部元素变为None（离队）
    self._front = (self._front + 1) % len(self._data)
    self._size -= 1
    return answer

  def enqueue(self, e):
    """Add an element to the back of queue."""
    if self._size == len(self._data):
      self._resize(2 * len(self.data))     # double the array size
    avail = (self._front + self._size) % len(self._data)
    self._data[avail] = e
    self._size += 1

  def _resize(self, cap):                  # we assume cap >= len(self)
    """Resize to a new list of capacity >= len(self)."""
    old = self._data                       # keep track of existing list
    self._data = [None] * cap              # allocate list with new capacity
    walk = self._front
    for k in range(self._size):            # only consider existing elements
      self._data[k] = old[walk]            # intentionally shift indices
      walk = (1 + walk) % len(old)         # use old size as modulus
    self._front = 0                        # front has been realigned

限于本书的篇幅，此处省略了＿＿len_＿和 is_empty 方法的具体实现。front 方法的实现也十分简单，因为当假定列表不为空时， front 索引能够精确地告诉我们目标元素在＿data 列表的什么位置。

添加和删除元素

入队方法的目的是在队列的尾部添加一个新的元素。我们需要确定适当的索引，并将新元素插入对应的位置中。虽然我们没有明确地为队列的尾部信息维护一个实例化变量，但是可以利用下面的公式计算下一个插入的位置：

avail = (self._front + self._size) % len(self._data)

注意，在插入新元素时，要使用这个队列的大小。例如，考虑一个存储容量为 10 的队 列，当前的队列长度为 3，并且第一个元素所在的索引为 5, 这个队列中已有的 3 个元素的存储位置即为索引 5 、6 和 7, 因此，新的元素应该被放置在索引为 (front + size) = 8 的位置上。

在一个首尾相连的循环队列实例中，利用模运算可以实现这种想要的循环语义。例如， 如果假设的队列有 3 个元素并且第一个元素在索引 8 的位置上，我们通过计算 (8 + 3)%10 得到结果为 1, 这样的结果完全正确，因为 3 个现有的元素占据索引为 8 、9 和 0 对应的位置。

当调用 dequeue 操作时， self._front 的当前值指明将要被删除和返回的值的索引。我们为将要返回的元素保存一个本地的引用，在从列表中删除该对象的引用之前，设 answer = self._ data[self._front] ，并设 self._data[self._front] = None 。设为 None 的原因与 python 回收未使用空间的机制有关。在内部， python 对已存的对象维护了一个对其的引用计数的计数器。如果计数变为 0, 这个对象实际上就无法访问，那么系统会回收这部分的内存以备将来使用（详细内容参见 15.1.2 节） 。由于我们不再负责存储一个已经离队元素，因此将从列表中删除该元素的引用以减少这个元素的引用计数。

dequeue 操作的第二个重要任务是更新＿front 的值以反映元素的移除，并将第二个元素变成新的第一个元素。在大多数情况下，我们可以简单地通过让索引值加 “ 1 " 更新，但是由于存在环式处理的可能，我们通常是依靠模运算处理，这在本节前面已经有详细的 描述。

调整队列的大小

当依次调用 enqueue 操作，且队列的大小恰好和底层存储的列表大小相等时，我们可以使用倍增底层列表存储大小的标准技术。通过这种方式，我们可以用与 5.3.1 节实现 DynamicArray 方法类似的方式实现这个操作。

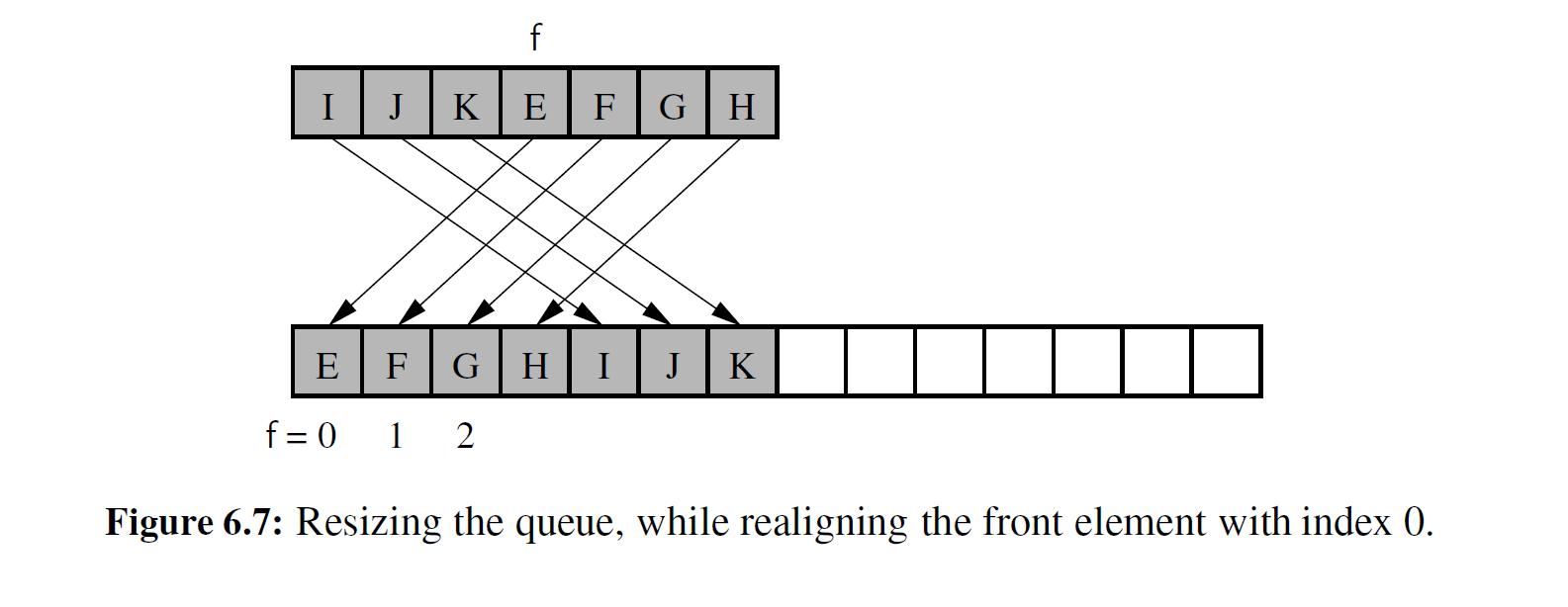
然而，在队列中的＿resize 方法上，要比在实现 DynamicArray 类的相关方法上更加谨慎：在对这个旧列表创建一个临时的引用后，我们分配了一个是原来旧列表 2 倍大小的新列表，并且将引用信息从旧列表复制到新列表中。在传输内容的同时，我们故意在新的数组中将队列的首部索引调整为 0，如图 6-7 所示。这种调整并不单纯为了好看。由于这个模算法依赖于数组的大小，因此将每个元素转移到新的数组并维持与原来相同的索引时，状态将会存在问题。

缩减底层数组

队列实现过程中，理想的性能是有 O(n) 的空间复杂度，其中 n 指的是当前队列中元素的个数。正如代码段 6-6 和代码段 6-7 给出的， ArrayQueue 的实现并不具备这种属性。当在队列满的状态下调用 enqueue 操作时，底层的存储数组就要进行扩展，但是调用出队操作的时候却并不会进行缩减数组的大小的处理。这样处理的结果是，底层的存储数组的大小是队列曾存储的最多元素的个数，而不是当前元素的个数。

我们在 5.3.2 节的动态数组部分讨论过这个问题，在随后的练习 C- 5.16 ~ C-5.20 中将 继续讨论这个问题。无论什么时候，当所存储的元素降低到数组总存储能力的 1/4 时， 一个健壮的方法是将这个数组大小缩减到当前容量的一半。这一处理可以通过在 dequeu e 方法中 插入如下两行代码来实现，只需要追加在代码段 6 -6 的第 38 行减少 self._size 处理部分之后即可，用于反映一个元素的丢失。

if O < self._size < len(self._data) // 4
  self._resize(len(self._data) // 2)

对基于数组的队列实现的分析

在考虑利用上述改进方法来不时缩小数组的大小进行维护队列处理的前提下， 表 6-3 列出了基于数组实现队列抽象数据类型的性能。除了＿resize 程序，所有的方法都依赖于一个常数数量的算术操作、比较和赋值等语句。因此，除了 enqueue 和 dequeue 操作是具有均摊 复杂度边界为 O(1) ，其余的每一个方法在最坏的情况下运行时间为 O(1) ，其原因与 5.3 节 给出的相似。

6.3 双端队列

接下来考虑一个类队列数据结构，它支持在队列的头部和尾部都进行插入和删除操作。这样一种结构被称为双端队列( double-ended queue 或者 deque ) ，它的发音通常为“deck", 以免与通常的队列抽象数据类型的方法 dequeue 相混淆，后者的发音类似于 “D.Q" 的缩写。

双端队列的抽象数据类型比栈和队列的抽象数据类型要更普遍。在一些应用中，这些额外的普遍性是非常有用的， 例如使用一个队列来描述餐馆当中的等餐队列。一般情况下，第 一个人会在发现餐馆中没有空闲的桌子时从队列的前面离开，而这个时候餐馆会重新在队列 的前面插入一个人。同样，处于队列尾部的顾客也可能由于不耐烦而离开队伍。（如果想模拟顾客从其他位置离开，我们需要一个更加通用的数据结构）

6.3.1 双端队列的抽象数据类型

为了提供一个相类似的抽象，可以定义双端队列的抽象数据类型 D , 这个 ADT 支持如下方法：

• D.add_first(e) ：向双端队列的前面添加一个元素 e 。
• D.add_last(e)：在双端队列的后面添加一个元素 e 。
• D.delete_first()：从双端队列中移除并返回第一个元素。若双端队列为空， 则触发一个错误。
• D.delete_last() ：从双端队列中移除并返回最后一个元素。若双端队列为空， 则触发一个错误。

此外，双端队列的抽象数据类型还包括如下的方法：

• D.first() ：返回（但不移除）双端队列的第一个元素。若双端队列为空， 则触发一个错误。
• D.last()：返回（但不移除）双端队列的最后一个元素。若双端队列为空， 则触发一个错误。
• D.is_empty()：如果双端队列不包含任何一个元素，则返回布尔值 "True” 。
• len(D)：返回当前双端队列中的元素个数。在 python 中．我们用＿＿len_＿ 这个特殊 的方法实现。

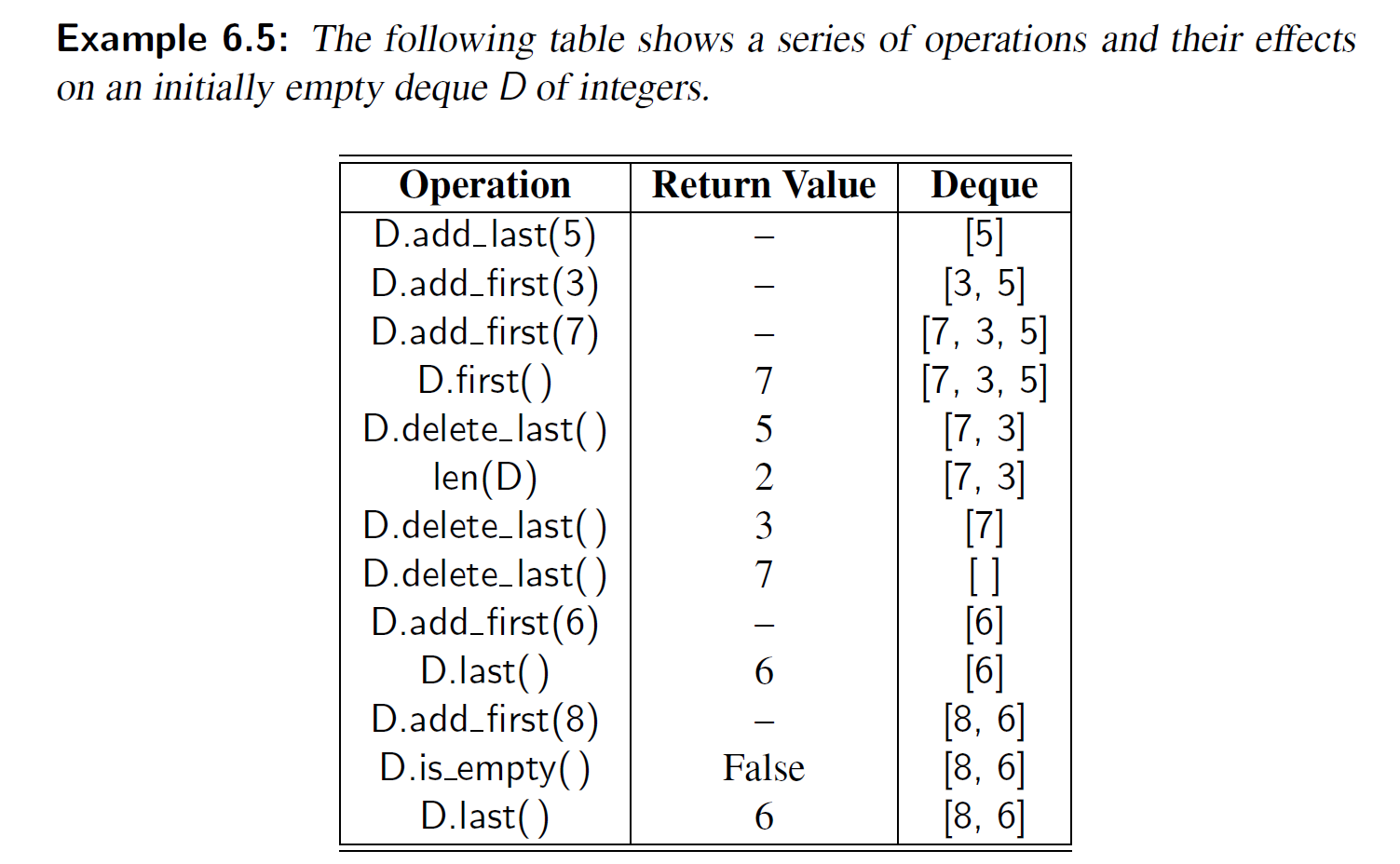
例题 6-5: 下表展示了一系列双端队列的操作和它们在一个初始化为整数类型的空双端队列中的效果。

6.3.2 使用环形数组实现双端队列

我们可以使用与代码段 6-6 和代码段 6-7 提供的实现 ArrayQueue 类相同的方法来实现双端队列的抽象数据类型（我们把通过 ArrayQueue 实现双端队列的细节留在了练习 P-6.32 中） 。我们建议保持 3 个相同的实例变量： ＿data 、_size 和＿front 。无论什么时候，只要想知道双端队列的尾部索引，或者超过队尾的第一个可用的位置，我们就可以通过模运算计算得 出。例如，方法 last()就是使用如下索引公式来实现的

back = (self._front + self._size - 1) % len(self._data)

对于方法 ArrayDeque.add_last , 我们采用了与方法 ArrayQueue .add_last 相同的实现方法，也利用了一个 _resize 程序。类似地，ArrayDeque.delete_first 方法的实现与 ArrayQueue.dequeue 方法相同。实现 add_first 与 delete_last 采用了相似的技术，其中的一处不同是，在调用 add_first 时需要循环处理数组起始位置，因此我们借助模（取余）运算来循环地计算索引值

self._front = (self._front - 1) % len(self._data) # cyclic shift

基于数组的双端队列 ArrayDeque 与基于数组的队列 ArrayQueue 的效率很相似，所有 操作都能在 O(1) 内能完成，但是由于有些操作的时间边界将会摊销，这可能会改变底层数组的大小。

6.3.3 python collections 模块中的双端队列

python 的标准 collections 模块中包含对一个双端队列类的实现方法。表 6-4 给出了 collections.deque 类最常用的方法。这里使用了比之前的抽象数据类型更加不对称的命名。

双端队列集合的接口选用与已经建立的 python 列表类命名约定一致，因为 pop 方法与 append 方法都被认为是在列表的尾部操作。因此， appendleft 和 popleft 都指的是在列表的首部操作。库双端队列同样也模仿了一个列表，因为它是一个带索引的序列，允许使用 D[j] 的语法任意访问和修改。

库双端队列的构造函数同样支持一个可选的 maxlen 参数以建立一个固定长度的双端队列。然而，当双端队列满时，如果在队列的任意一端调用 append 方法，它并不会触发一个错误；相反，这会导致在相反一端移除一个元素。也就是说，当队列满时，调用 appendleft 方法会导致右端一个隐藏的 pop 调用发生，以便为新加入的元素腾出空间。

当前 python 版本使用了一个混合的方法实现 collection.deque, 这种方法使用了循环数组，这些循环数组被组合到块中，而这些块本身又被组织进一个双向链表中（我们将在下一 章介绍这种数据结构） 。双端队列类保证在任何一端操作的耗时为 O(1) ，但在最坏的操作情 况下，当使用靠近双端队列中部附近的索引时，耗时将为 O(n) 。

6.4 练习

巩固

R-6.1 如果在一个初始化为空的栈上执行如下一系列操作，将返回什么值？push(5), push(3), pop(), push(2), push(8), pop(), pop(), push(9), push(1), pop(), push(7), push(6), pop(), pop(), push(4) pop(), pop() 。

R-6.2 假设一初始化为空的栈 S 已经执行了 25 个 push 操作、12 个 top 操作和 10 个 pop 操作，其中 3 个触发了栈空错误。请问 S 目前的大小是多少？

R-6.3 实现一个函数 transfer(S, T) 将栈 S 中的所有元素转移到栈 T 中，使位于 S 栈顶的元素被第一个插人栈 T 中， 使位于 S 栈底的元素最后被插入栈 T 的顶部。

R-6.4 给出一个用于从栈中移除所有元素的递归实现方法。

R-6.5 实现一个函数，通过将一个列表内的元素按顺序压入堆栈中，然后逆序把它们写回到列表中， 实现列表的逆置。

R-6.6 给出一个算术表达式中分组符号匹配的精确而完整的定义。应保证定义可以是递归的。

R-6.7 如果在一个初始化为空的队列上执行如下一系列操作后，返回值是什么？ enqueue(5), enqueue(3), dequeue(), enqueue(2), enqueue(8), dequeue(), dequeue(), enqueue(9),enqueue(1), dequeue(), enqueue(7), enqueue(6), dequeue(), dequeue(), enqueue(4), dequeue(), dequeue()

R-6.8 假设一个初始化为空的队列 Q 巳经执行了共 32 次入队操作、10 次取首部元素操作和 15 次出队橾作，其中 5 次触发了队列为空的错误。队列 Q 目前的大小是什么？

R-6.9 假定先前所述间题的队列是 ArrayQueue 的实例且初始化为 30, 并且假定它的大小不会超过 30, 那么 front 实例变量的最终值是多少？

R-6.10 试想，如果代码段 6-7 ArrayQueue. Resize 方法中的第 53 ~ 55 行执行如下 loop 循环将会发生什么？ 给出错误的详细解释。

for k in range(self._size)
  self._data[k] = old[k]

R-6.11 给出一个简单的适配器实现队列 ADT, 其中采用一个 collections.deque 实例做存储。

R-6.12 在一个初始化为空的双端队列中执行以下一系列操作，将会返回什么结果？ addfirst(4), add_last(8), add last(9), add first(5), back(), delete* first(), delete last(), add last(7), first(), last(),add last(6), delete* first(), deletefirst() 。

R-6.13 假设有一个含有数字(1,2,3,4,5,6,7,8) 并按这一顺序排列的双端队列 D，并进一步假设有一个初始化为空的队列 Q 。给出一个只用 D 和 Q （不包含其他变量）实现的代码片段，将元素(1, 2, 3, 5, 4, 6, 7, 8) 按这一顺序存储在 D 中。

R-6.14 使用双端队列 D 和一个初始化为空的栈 S 重复做上一问题

创新

C-6.15 假设爱丽丝选择了 3 个不同的整数， 并将它们以随机顺序放置在栈 S 中。写一个简短的顺序型的伪代码（不包含循环或递归），其中只包含一次比较和一个变量 x, 使得爱丽丝的 3 个整数中最大的以 2/3 概率存储在变量 x 中，试说明你的方法为什么是正确的。

C-6.16 修改基于数组的栈的实现方法，使栈的容量限制在最大元素数量 maxlen 之内。该最大数量对于构造函数（默认值为 none ) 是一个可选参数。如果 push 操作在栈满时被调用，则抛出一个“栈满“异常（与栈空异常定义类似） 。

C-6.17 在之前实现栈的练习中，假设底层列表是空的。重做该练习，此时预分配一个长度等于堆栈 最大容量的底层列表。

C-6.18 如何用练习 R-6.3 中描述的转换函数和两个临时栈来取代一个给定相同元素但顺序逆置的栈。

C-6.19 在代码段 6-5 中，假设 HTML 的开始标签具有 与

的形式。更普遍的是， HTML 允许可选的屈性作为开始标签的一部分。所用的一般格式是 ；例如，表可以通过使用开始标签 <table border="3" cellpadding="5"＞被赋予一个边界和附加数据。修改代码段 6-5, 使得即使在一个开始标签包含一个或多个这样的属性时，也可以正确匹配标记。

C-6.20 通过一个栈实现一个非递归算法来枚举 {1, 2, ··· , n} 所有排列数结果。

C-6.21 演示如何使用栈 S 和队列 Q 非递归地生成一个含 n 个元素的集合所有可能的子集集合 T。

C-6.22 后缀表示法是一种书写不带括号的算术表达式的简明方法。它是这样定义的： 如果” (exp1 ) OP(exp2 )" 是一个普通、完整的括号表达式，它的操作符是 OP, 那么它的后缀版本为 “pexp1 是 pexp2 OP" 、其中 pexp1 是 exp 1 的后缀表示形式， pexp2 是 exp2 的后缀表示形式。一个单一的数字或变址的后缀表示形式就是这个数字或变量。例如，” ((5 + 2)*(8 - 3))/4 " 的后缀版本为 “52 + 83 - *4/ ＂ 。写出一种非递归方式实现的后缀表达式转换算法。

C-6.23 假设有 3 个非空栈 R 、S 、T。请通过一系列操作，将 S 中的元素以其原始的顺序存储到 T 中 原有元素的后面，最终 R 中元素的顺序不变。例如， R=[1, 2, 3], S=[4, 5], T=[6, 7, 8, 9] ，则最终的结果应为 R=[1,2, 3], S=[6, 7, 8, 9, 4, 5] 。

C-6.24 描述如何用一个简单的队列作为实例变址实现堆栈 ADT , 在方法体中，只有常量占用本地内 存。在你所设计的方法中， push()、pop()、top()的运行时间分别是多少？

C-6.25 描述如何用两个栈作为实例变量实现队列 ADT, 这样使得所有队列操作的平均时间开销为 O(1) 。给出一个正式的证明。

C-6.26 描述如何使用一个双端队列作为实例变量实现队列 ADT。该方法的运行时间是多少？

C-6.27 假设有一个包含 n 个元素的栈 S 和一个初始为空的队列 Q, 描述如何用 Q 扫描 S 来查看其中是否包含某一特定元素 x, 算法必须返回到元素在 S 中原来的位置。算法中只能使用 S 、Q 和 固定数量的变量。

C-6.28 修改 ArrayQueue 实现方法，使队列的容量由 maxlen 限制， 其中该最大长度对于构造函数 （默认为 none ) 来说是一个可选参数。如果在栈满的时候调用 enqueue 操作，则触发一个队列满异常（与队列空异常定义类似） 。

C-6.29 在队列 ADT 的某些特定应用中，以某种方式对一个元素反复执行入队出队操作是很常见的。改造基于数组的队列实现方法，加入一个 rotate()操作，这个操作与 Q.enqueue 和 Q.dequeue 的结合具有相同的语义特征。然而，它的执行效率应当比分别调用两个方法更有效（例如． 该方法中不需要修改队列的长度＿size) 。

C-6.30 爱丽丝有两个用于存储整数的队列 Q 和 R 。鲍勃给了爱丽丝 50 个奇数和 50 个偶数，并坚待让她在队列 Q 和 R 存储所有 100 个整数。然后他们玩了一个游戏，鲍勃从队列 Q 和 R 中随机选择元素（采用在本章所描述的循环调度，其对于选择队列的次数是随机的） 。如果在游戏结束时被处理的最后一个数是奇数，则鲍勃胜。爱丽丝能如何分配整数到队列中来优化她获胜的机会？她获胜的机会是什么？

项目

P-6.32 如 6.3.2 节描述的那样，给出一个完整的基于数组的双端队列 ADT 的队列实现方法。

P-6.33 给定一个基于数组实现双端队列的实现方法、使其支持表 6-4 列出的 collection.deque 类的 所有公共操作，包括使用 maxlen 这个可选参数。当一个限制长度的队列已满时，提供与 collections.deque 类相似的语义， 使一个调用将一个元素插入双端队列的尾部时造成相反方向一个元素的丢失

P-6.34 实现一个程序，可以输入以后缀形式表示的符数表达式（ 见练习 C-6 .22 ) 并且输出它的运算 结果。

P-6.35 6.1 节的介绍表明，栈通常用于在应用程序中提供｀撤销＂支持，如网络浏览器或文本编辑器。虽然支持撤销可以用无界堆栈来实现，但许多应用程序只使用容量固定的堆栈提供有限步的撤销操作。当压栈操作在满栈时被调用，并不是抛出栈满异常，见练习 C-6.16) ， 一个更典型的语义是接受在顶部压栈的元素，同时在栈底部“漏出“最老的元素来腾出空间。

P-6.36 当出售一支由若干家公司共享的公共股票时，共享售出价和原始买入价的资本收益（或者． 有时候亏损）是不同的。对于单一共享的股票这个规则很容易理解｀但如果出售的是一支已经购买了很久的共享股票时，我们必须鉴别这支共享股票是真的在出售。在这个例子中，对 于识别哪个共享股票被卖掉的问题， 一个标准的判断原则就是采用 FIFO 协议一一这支被共享出售的股票，往往是那些持有时间最长的（ 实际上，这种默认的方法已被封装到了几款个人投资软件包中） 。例如．假设买 100 股共享股票，第一天的价格为每股 20 美元，第二天有 20 股的价格是 24 美元．第三天有 200 股的价格为 36 美元，而在第四天以每股 30 美元的价格买出 150 股。根据 FIFO 的原则，意味着 150 股被卖掉． 第一天买了 100 股，第二天买了 20 股，第三天买了 30 股， 因此在这个例子中的资本收益就应该是： 100 x 10 + 20 x 6 + 30 x (- 6) 或者 940 美元。写一个程序，用于表示形如“以每股 y 美元的价格购买了 x 股 share (s) 股票” 或者”以每股 y 美元的价格卖出 x 股 share(s) 股票”的一组事务的序列，假定这些事务发生在连续的几天之内，同时 x 和 y 的值都是整数。当给定了一个输入序列． 运用 FIFO 协议来识别共享股票，对应的输出序列应该是整个序列总的资本收益的值（或者资本亏损的值） 。

P-6.37 设计一个两色双向栈 ADT, 其中包含两个栈，即一个 “ 红＂栈和一个 “ 蓝＂栈， 并包含和常规栈操作一致的有颜色编码的栈操作。例如，在这个 ADT 中，支持一个 “ 红 ” 压栈操作和一 个 “ 蓝 ” 出栈操作。给出一种有效的实现方法，即采用一个限定容量为 N 的单个数组来实现这个 ADT, 假定 N 值始终大于单个的 “ 红＂栈与 “ 蓝＂栈大小之和