第 7 章 链表(Linked Lists)
在第 5 章, 我们仔细探讨了 python 的基于数组的 list 类。在第 6 章,我们着重讨论使用这个类来实现经典的栈、队列、双向队列的抽象数据类型(Abstract Data Type, ADT) 。
python 的 list 类是高度优化的,并且通常是考虑存储问题时很好的选择。除此之外, list 类 也有一些明显的缺点:
- 一个动态数组的长度可能超过实际存储数组元素所需的长度。
- 在实时系统中对操作的摊销边界是不可接受的。
- 在一个数组内部执行插入和删除操作的代价太高。
在本章,我们介绍一个名为链表的数据结构,它为基于数组的序列提供了另一种选择 (例如 python 列表) 。基于数组的序列和链表都能够对其中的元素保持一定的顺序,但采用的方式截然不同。数组提供更加集中的表示法,一个大的内存块能够为许多元素提供存储和 引用。相对地, 一个链表依赖于更多的分布式表示方法,采用称作节点的轻量级对象,分配给每一个元素。每个节点维护一个指向它的元素的引用,并含一个或多个指向相邻节点的引用,这样做的目的是为了集中地表示序列的线性顺序。
我们将对比基于数组序列和链表的优缺点。通过数字索引 k 无法有效地访问链表中的元素,而仅仅通过检查一个节点,我们也无法判断出这个节点到底是表中的第 2 个、第 5 个还是第 20 个元素。然而,链表避免了上面提到的基于数组序列的 3 个缺点
7.1 单向链表¶
帮助理解:Wiki 上对单向链表的定义:¶
链表中最简单的一种是单向链表,它包含两个域,一个信息域和一个指针域。这个链接指向列表中的下一个节点,而最后一个节点则指向一个空值。
> 一个单向链表包含两个值: 当前节点的值和一个指向下一个节点的链接
一个单向链表的节点被分成两个部分。第一个部分保存或者显示关于节点的信息,第二个部分存储下一个节点的地址。单向链表只可向一个方向遍历。
链表最基本的结构是在每个节点保存数据和到下一个节点的地址,在最后一个节点保存一个特殊的结束标记,另外在一个固定的位置保存指向第一个节点的指针,有的时候也会同时储存指向最后一个节点的指针。一般查找一个节点的时候需要从第一个节点开始每次访问下一个节点,一直访问到需要的位置。但是也可以提前把一个节点的位置另外保存起来,然后直接访问。当然如果只是访问数据就没必要了,不如在链表上储存指向实际数据的指针。这样一般是为了访问链表中的下一个或者前一个(需要储存反向的指针,见下面的双向链表)节点。
相对于下面的双向链表,这种普通的,每个节点只有一个指针的链表也叫单向链表,或者单链表,通常用在每次都只会按顺序遍历这个链表的时候(例如图的邻接表,通常都是按固定顺序访问的)。
单向链表最简单的实现形式就是由多个节点的集合共同构成一个线性序列。每个节点存储一个对象的引用,这个引用指向序列中的一个元素,即存储指向列表中的下一个节点,如图 7- 1 和图 7 -2 所示。

图 7- 1 节点实例的示例,用于构成单向链表的一部分。这个节点含有两个成员:元素成员引用一个任意的对象,该对象是序列中的一个元素(在这个例子中,序列指的是机场节点 MSP ) ; 指针域成员指向单向链表的后继节点(如果没有后继节点,则为空)
链表的第一个和最后一个节点分别为列表的头节点和尾节点。从头节点开始,通过每个节点的 " next " 引用,可以从一个节点移动到另一个节点,从而最终到达列表的尾节点。若 当前节点的 " next " 引用指向空时, 我们可以确定该节点为尾节点。这个过程通常叫作遍历链表。由于一个节点的 " next " 引用可以被视为指向下一个节点的链接或者指针,遍历列表的过程也称为链接跳跃或指针跳跃。

图 7 -2 元素是用字符串表示机场代码的单向链表示例。列表实例中维护了一个叫作头节点( head ) 的成员,它标识列表的第一个节点。在某些应用程序中,另有一个叫作尾节点 (tail) 的成员,它标识列表的最后一个节点。空对象被表示为 \(\empty\)
链表在内存中的表示依赖于许多对象的协作。每个节点被表示为唯一的对象,该对象实例存储着指向其元素成员的引用和指向下一个节点的引用(或者为空) 。另一个对象用于代表整个链表。链表实例至少必须包括一个指向链表头节点的引用。没有一个明确的头的引用,就没有办法定位节点(或间接地定位其他任何节点) 。没有必要直接存储一个指向列表尾节点的引用,因为尾节点可以通过从头节点开始遍历链表中的其余节点来定位。不管怎样,显式地保存一个指向尾节点的引用, 是避免为访问尾节点而进行链表遍历的常用方法。类似地,链表实例保存一定数量的节点总数(通常称为列表的大小) 也是比较常见的,这样就可以避免为计算链表中的节点数量而需要遍历整个链表
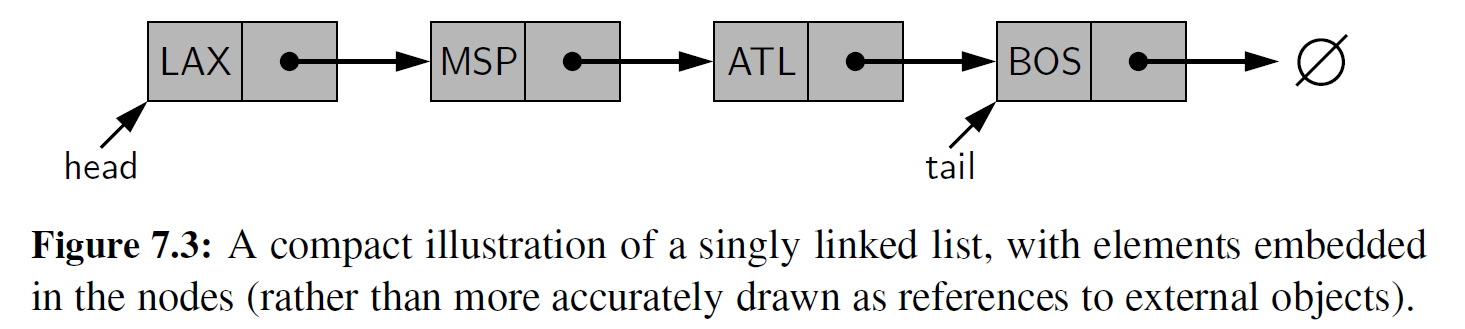
在本章的其余部分,我们将继续把节点称为 “对象”,而把每个节点指向 “ next " 节点的引用称为”指针" 。但是,为简单起见, 我们将一个节点的元素直接嵌入该节点的结构中, 尽管元素实际上是一个独立的对象。对此,图 7-3 以更简洁的方式展示了图 7-2 的链表。
在单向链表的头部插入一个元素¶
单向链表的一个重要属性是没有预先确定的大小, 它的占用空间取决于当前元素的个数。当使用一个单向链表时,我们可以很容易地在链表的头部插入一个元素,如图 7-4 所示, 伪代码描述如代码段 7-1 所示。其基本思想是创建一个新的节点,将新节点的元素域设置为新元素,将该节点的 " next " 指针指向当前的头节点,然后设置列表的头指针指向新节点。
代码段 7- 1 在单向链表 L 头部插入一个元素。注意,要在为新节点分配 L.head 变量之前设置新节点 的 "next" 指针。如果初始列表为空(即 L.head 为空),那么就将新节点的 “next" 指针指向空(None)
Algorithm add_first(L,e):
newest = Node(e) 创建新节点实例存储对元素 e 的引用
newest.next = L.head 设置新节点的下一个引用旧的头节点
L.head = newest 设置变量 head 以引用新节点
L.size = L.size + 1
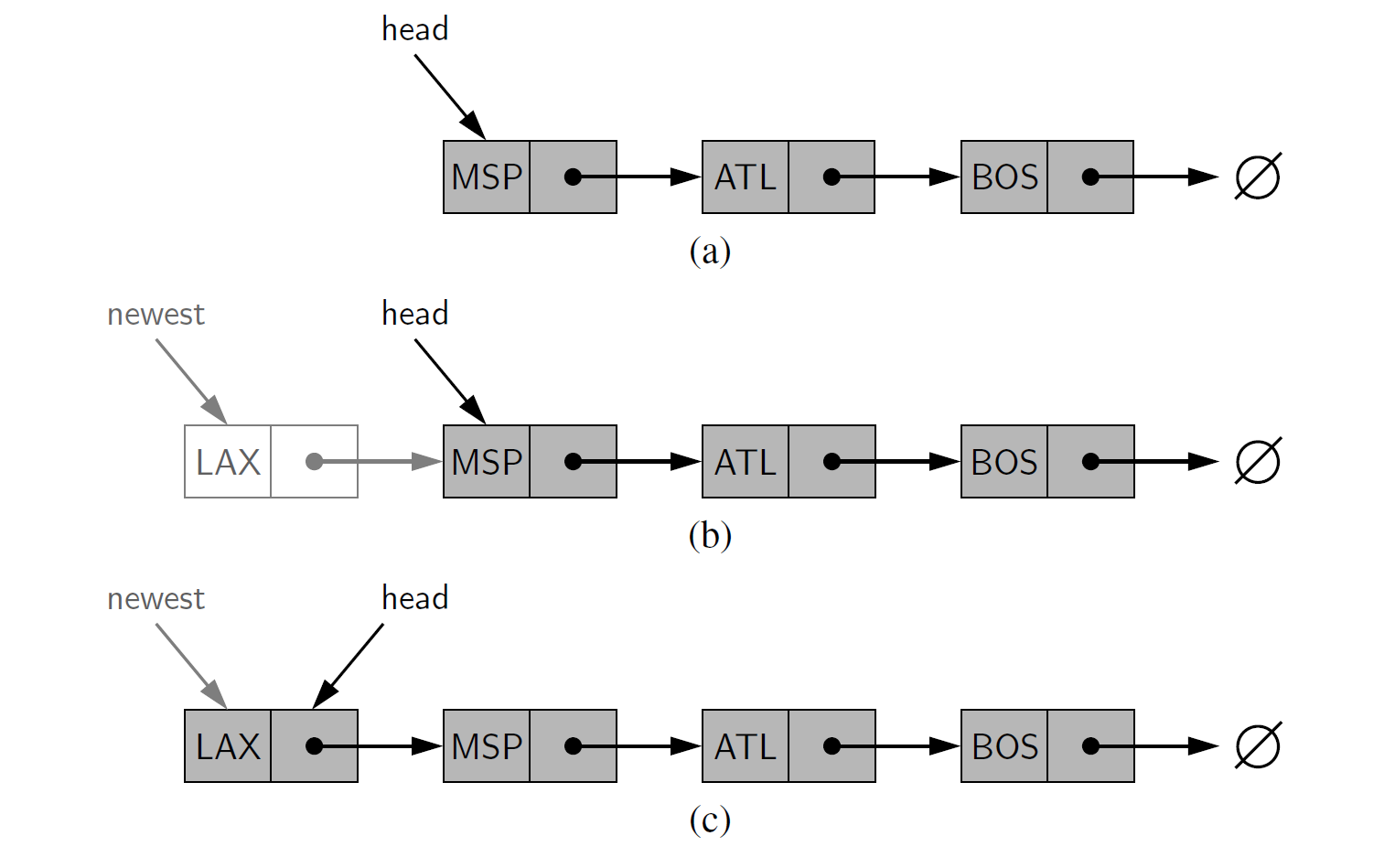
图 7-4 在单向链表的头部插入一个元素
在单向链表的尾部插入一个元素¶
只要保存了尾节点的引用(指向尾节点的指针),就可以很容易地在链表的尾部插入一个元素,如图 7-5 所示。在这种情况下,创建一个新的节点,将其 “ next " 指针设置为空, 并设置尾节点的 “ next " 指针指向新节点, 然后更新尾指针指向新节点,伪代码描述如代码段 7-2 所示。
代码段 7-2 在单向链表的尾部插入一个新的节点。注意,在设置尾指针指向新节点之前,设置尾节点的 “next" 指针指向原来的尾节点。当向一个空链表中插入新节点时,需要对这段代码进行一定的调整,因为空链表不存在尾节点
Algorithm add last(L,e):
newest = Node(e) {create new node instance storing reference to element e}
newest.next = None {set new node’s next to reference the None object}
L.tail.next = newest {make old tail node point to new node}
L.tail = newest {set variable tail to reference the new node}
L.size = L.size+1 {increment the node count}
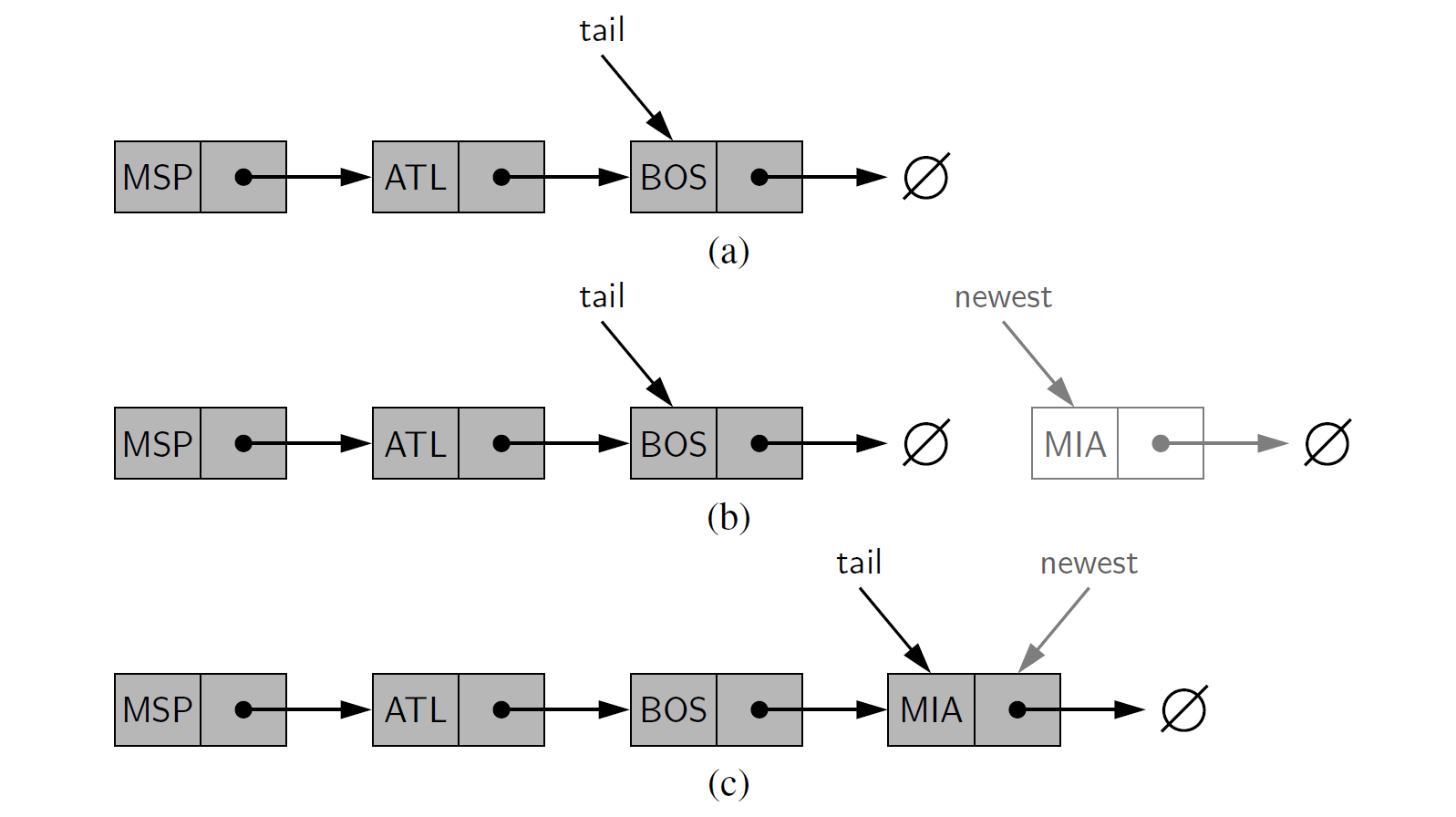
图 7-5 在单向链表的尾部插入一个元素
从单向链表中删除一个元素¶
从单向链表的头部删除一个元素,基本上是在头部插入一个元素的反向操作。这个操作的详细过程如图 7-6 和代码段 7-3 所示
Algorithm remove first(L):
if L.head is None then
Indicate an error: the list is empty.
L.head = L.head.next {make head point to next node (or None)}
L.size = L.size−1 {decrement the node count}
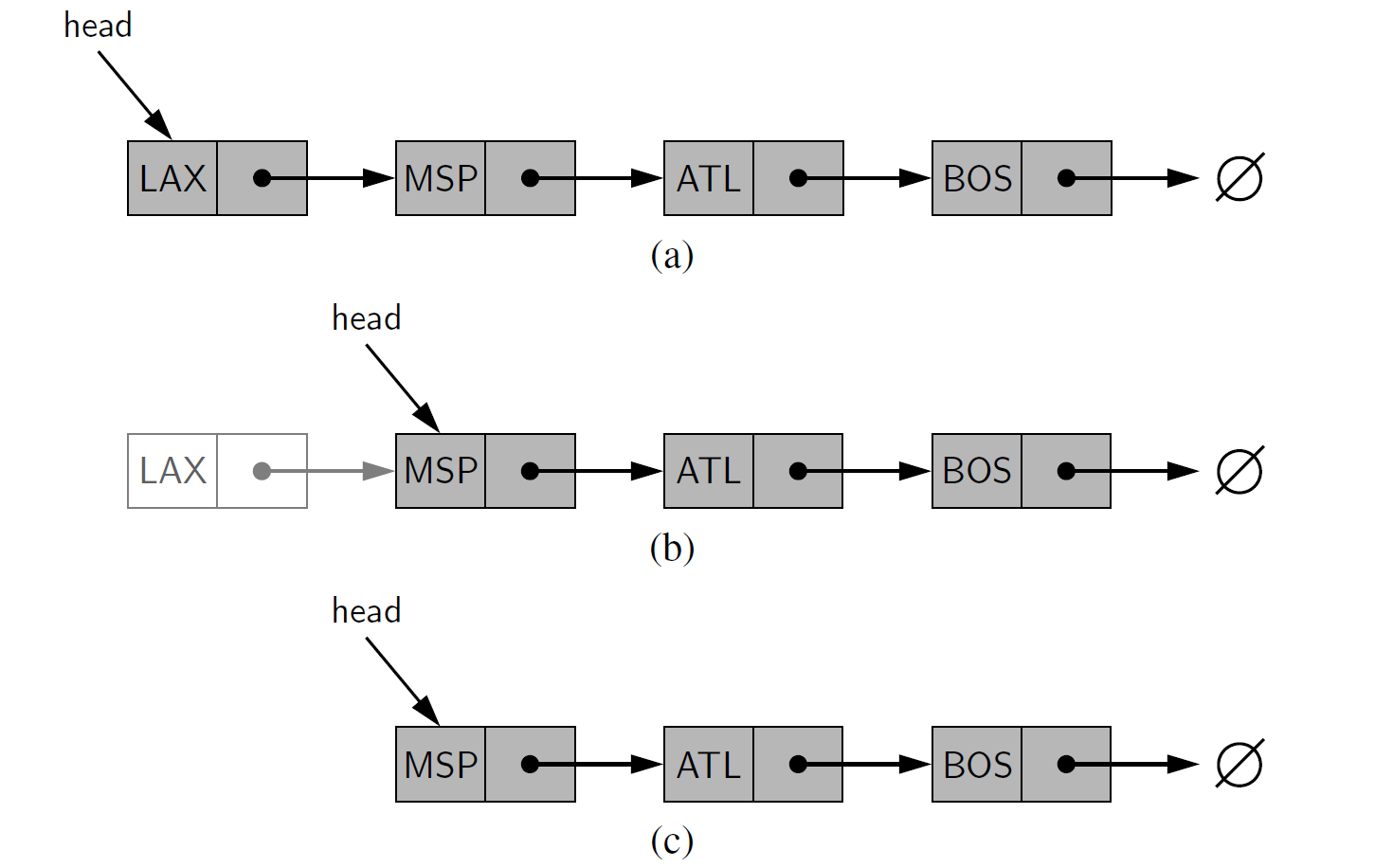
图 7-6 在单向链表的头部删除一个节点
不幸的是, 即使保存了一个直接指向列表尾节点的尾指针,我们也不能轻易地删除单向链表的尾节点。为了删除链表的最后一个节点,我们必须能够访间尾节点之前的节点。但是 我们无法通过尾节点的 "next" 指针找到尾节点的前一个节点,访问此节点的唯一方法是从链表的头部开始遍历整个链表。但是这样序列遍历的操作需要花费很长的时间,如果想要有效地实现此操作,需要实现双向列表(见 7.3 节) 。
可以看到,我们构建 Node 类的实例变量 Tr 储存的实际上是该变量的地址,因此在借助链表构建一些数据结构的过程中,可以让 next 方法直接 = 实例
另外,一张完整的链表不能以数组的角度进行思考,例如考虑链表的头部,按照这里
_Node的方法,只要取得链表的第一个变量就能得到整张链表(链表的所有元素都是嵌套的),这就是说,实际上链表的“第二个”元素就是第一个元素的self._next变量
7.1.1 用单向链表实现栈¶
在这一部分,我们将通过给出一个完整栈 ADT 的 python 实现来说明单向链表的使用 (见 6.1 节) 。设计这样的实现,我们需要决定用链表的头部或尾部来实现栈顶。最好的选择显而易见: 因为只有在头部,我们才能在一个常数时间内有效地插入和删除元素。由于所有 栈操作都会影响栈顶,因此规定栈顶在链表的头部。
为了表示列表中的单个节点,我们创建了一个轻量级_Node 类。这个类将永远不会直接暴露给栈类的用户,所以被正式定义为非公有的、最终的 LinkedStack 类的嵌套类(见 2.5.1 节) 。代码段 7-4 展示了_Node 类的定义。
class _Node:
”””Lightweight, nonpublic class for storing a singly linked node.”””
__slots__ = '_element' , '_next' # streamline memory usage
def __init__ (self, element, next): # initialize node’s fields
self._element = element # reference to user’s element
self._next = next # reference to next node
一个节点只有两个实例变量: _element 和 _next(元素引用和指向下一个节点的引用),为了提高内存的利用率,我们专门定义了__slots__(见 2.5.1 节),因为一个单向链表中可能有多个节点实例。_Node 类的构造函数是为了方便而设计的,它允许为每个新创建的节点赋值。
代码段 7-5 和代码段 7-6 给出了 LinkedStack 类的完整实现。每个栈实例都维护两个变量。头指针指向链表的头节点(如果栈为空,这个指针指向空) 。我们需要用变量_size 待续追踪当前元素的数量,否则,当需要返回栈的大小时,必须通过遍历整个列表来计算元素的 数量。
将元素压栈( push ) 的实现与代码段 7-1 所给出的在单向链表头部插入一个元素的伪代码基本一致。向栈顶放入一个新的元素 e 时,可以通过询用_Node 类的构造函数来完成链接结构的必要改变。代码如下:
self._head = self._Node(e,self._head)
注意,新节点的 _next指针域被设置为当前的栈顶节点,然后将头指针 (self._head) 指向新节点。
from ..exceptions import Empty
class LinkedStack:
"""LIFO Stack implementation using a singly linked list for storage."""
#-------------------------- nested _Node class --------------------------
class _Node:
"""Lightweight, nonpublic class for storing a singly linked node."""
__slots__ = '_element', '_next' # streamline memory usage
def __init__(self, element, next): # initialize node's fields
self._element = element # reference to user's element
self._next = next # reference to next node
#------------------------------- stack methods -------------------------------
def __init__(self):
"""Create an empty stack."""
self._head = None # reference to the head node
self._size = 0 # number of stack elements
def __len__(self):
"""Return the number of elements in the stack."""
return self._size
def is_empty(self):
"""Return True if the stack is empty."""
return self._size == 0
def push(self, e):
"""Add element e to the top of the stack."""
self._head = self._Node(e, self._head) # create and link a new node
self._size += 1
def top(self):
"""Return (but do not remove) the element at the top of the stack.
Raise Empty exception if the stack is empty.
"""
if self.is_empty():
raise Empty('Stack is empty')
return self._head._element # top of stack is at head of list
def pop(self):
"""Remove and return the element from the top of the stack (i.e., LIFO).
Raise Empty exception if the stack is empty.
"""
if self.is_empty():
raise Empty('Stack is empty')
answer = self._head._element
self._head = self._head._next # bypass the former top node
self._size -= 1
return answer
实现 top 方法时,目标是返回栈顶部的元素。当栈为空时,我们会抛出 Empty 异常,这个异常在第 6 章代码段 6-1 中巳经定义过了。当栈不为空时,头指针(self._head) 指向链表的第一个节点,栈顶元素可以表示为 self._head._element。
元素出栈操作 (pop) 的实现与代码段 7-3 中的伪代码基本一致。我们利用一个本地的指针指向要删除的节点中所保存的成员元素( element ) ,并将该元素返回给调用者 pop 。
表 7-1 给出了 LinkedStack 操作的分析。可以看到,所有方法在最坏情况下都是在常数时间内完成的。这与表 6-2 给出的数组栈的摊销边界形成了对比

7.1.2 用单向链表实现队列¶
正如用单向链表实现栈 ADT 一样,我们可以用单向链表实现队列 ADT, 且所有操作支持最坏情况的时间为 O(1) 。由于需要对队列的两端执行操作,我们显式地为每个队列维护一个_head 和一个_tail指针作为实例变量。一种很自然的做法是,将队列的前端和链表的头部对应,队列的后端与链表的尾部对应,因为必须使元素从队列的尾部进入队列,从队列的头部出队列(前面曾提到,我们很难高效地从单向链表的尾部删除元素) 。链表队列 ( LinkedQueue ) 类的实现如代码段 7-7 和代码段 7-8 所示。
from ..exceptions import Empty
class LinkedQueue:
"""FIFO queue implementation using a singly linked list for storage."""
#-------------------------- nested _Node class --------------------------
class _Node:
"""Lightweight, nonpublic class for storing a singly linked node."""
__slots__ = '_element', '_next' # streamline memory usage
def __init__(self, element, next):
self._element = element
self._next = next
#------------------------------- queue methods -------------------------------
def __init__(self):
"""Create an empty queue."""
self._head = None
self._tail = None
self._size = 0 # number of queue elements
def __len__(self):
"""Return the number of elements in the queue."""
return self._size
def is_empty(self):
"""Return True if the queue is empty."""
return self._size == 0
def first(self):
"""Return (but do not remove) the element at the front of the queue.
Raise Empty exception if the queue is empty.
"""
if self.is_empty():
raise Empty('Queue is empty')
return self._head._element # front aligned with head of list
def dequeue(self):
"""Remove and return the first element of the queue (i.e., FIFO).
Raise Empty exception if the queue is empty.
"""
if self.is_empty():
raise Empty('Queue is empty')
answer = self._head._element
self._head = self._head._next
self._size -= 1
if self.is_empty(): # special case as queue is empty
self._tail = None # removed head had been the tail
return answer
def enqueue(self, e):
"""Add an element to the back of queue."""
newest = self._Node(e, None) # node will be new tail node
if self.is_empty():
self._head = newest # special case: previously empty
else:
self._tail._next = newest
self._tail = newest # update reference to tail node
self._size += 1
用单向链表实现队列的很多方面和用 LinkedStack 类实现非常相似,如嵌套_Node类 的定义。链表队列的 LinkedQueue 的实现类似于 LinkedStack 的出栈,即删除队列的头部节点,但也有一些细微的差别。因为队列必须准确地维护尾部的引用(栈的实现中没有维持这样的变量) 。通常,在头部的操作对尾部不产生影响。但在一个队列中调用元素出队列操作时,我们要同时删除列表的尾部。同时,为了确保一致性,还要设置 self._tail 为 None 。
在 LinedQueue 的实现问题中,有一个相似的复杂操作。最新的节点往往会成为新的链表尾部,然而当这个新节点是列表中的唯一节点时,就会有所不同。在这种情况下,该节点也将变成新的链表头部;否则,新的节点必须被立即链接到现有的尾部节点之后。
在性能方面, LinkedQueue 与 LinkedStack 类似,所有操作在最坏情况下运行的时间为常数,而空间使用率与当前元素数量呈线性关系。
7.2 循环链表¶
在 6 .2 .2 节中,我们引入了"循环“数组的概念,并且说明了如何用其实现队列 ADT 。在实现中,循环数组的概念是人为定义的,因此,在数组内部自身的表示中没有任何循环结构。这是我们在使用模运算中,将一个索引从最后一个位置 ”推进”到第一个位置时所提供 的一个抽象概念。
在链表中,我们可以使链表的尾部节点的 " next " 指针指向链表的头部,由此来获得一 个更切实际的循环链表的概念。我们称这种结构为循环链表,如图 7-7 所示。
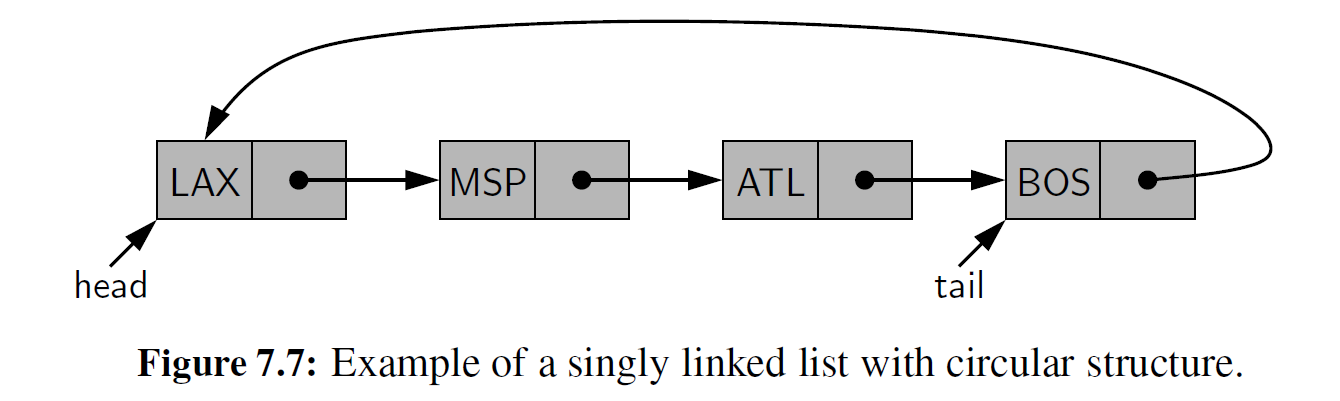
与标准的链表相比,循环链表为循环数据集提供了一个更通用的模型,即标准链表的开始和结束没有任何特定的概念。图 7-8 给出了一个相对图 7 -7 中循环列表的结构更对称的示意图。
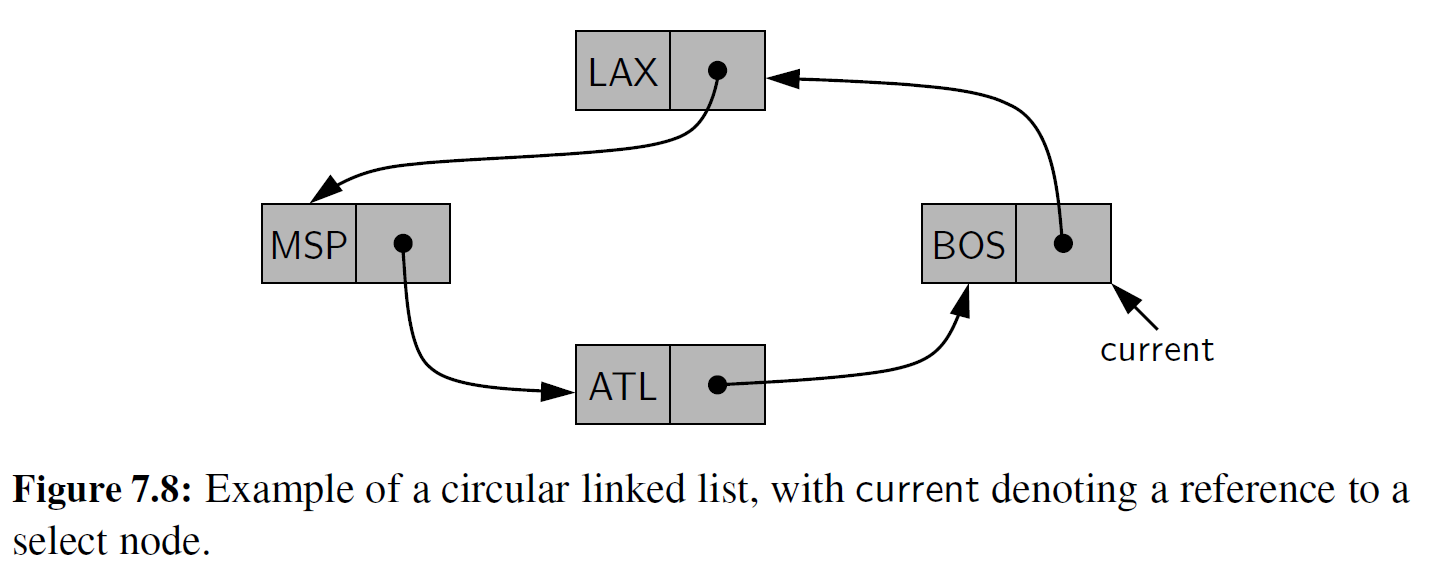
我们也可以使用其他类似于图 7-8 所示的环形视图,例如,描述美国芝加哥环线上的火车站点顺序或选手在比赛中的轮流顺序。虽然一个循环链表可能并没有开始或者结束节点, 但是必须为一个特定的节点维护一个引用,这样才能使用该链表。我们采用 “current" 标识 符来表示一个指定的节点。通过设置 current = current.next , 我们可以有效地遍历链表中的各 个节点。
7.2.1 轮转调度¶
为了说明循环链表的使用,我们来讨论一个循环调度程序,在这个调度程序中,以循环的方式迭代地遍历一个元素的集合,并通过执行一个给定的动作为集合中的每个元素进行 “服务” 。例如,使用这种调度程序,可以公平地分配那些必须为一个用户群所共享的资源。 比如,循环调度经常用于为同一计算机上多个并发运行的应用程序分配 CPU 时间片。
使用普通队列 ADT , 在队列 Q 上反复执行以下步骤(见图 7-9 ) ,这样就可以实现循环调度程序:
- e = Q.dequeue()
- Service element e
- Q.enqueue(e)
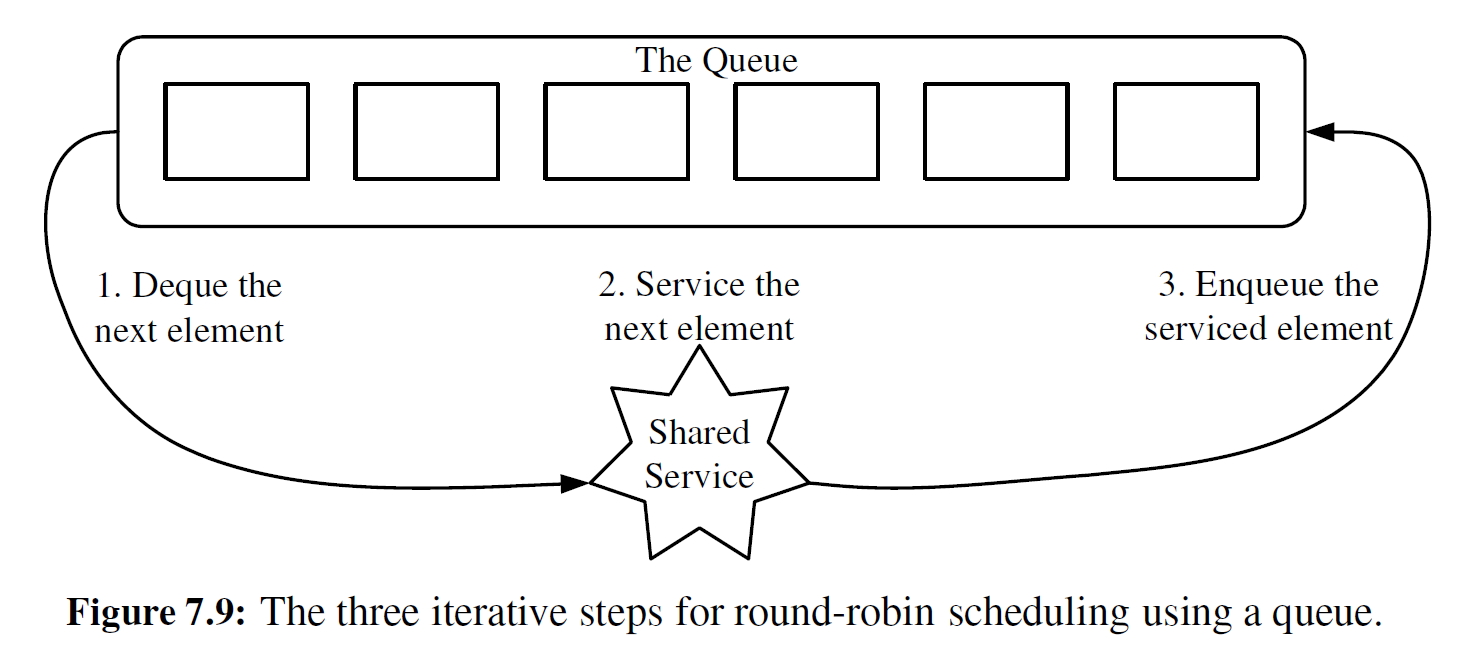
如果用 7.1.2 节介绍的 LinkedQueue 类来实现这个应用程序,则没有必要急于对那种在结束不久后就将同一元素插入队列的出队列操作进行合并处理。从列表中删除一个节点,相应地要适当调整列表的头并缩减列表的大小;对应地,当创建一个新的节点时,应将其插入 列表的尾部并且增加列表的大小。
如果使用一个循环列表,有效地将一个项目从队列头部转换成队列尾部,可以通过访问标记队列边界的引用来实现。接下来,我们会给出一个用于支持整个队列 ADT 的循环队列类的实现,并介绍一个附加的方法 rotate(), 该方法用于将队列中的第一个元素移动到队列尾部(在 python 模块集合的双端队列类中,支持一个类似的方法,参见表 6-4 ) 。使用这个操作循环调度程序,可以通过重复执行以下步骤有效地实现循环调度算法:
- Service element Q. front()
- Q.rotate()
7.2.2 用循环链表实现队列¶
为了采用循环链表实现队列 ADT, 我们用图 7-7 给出直观示意:队列有一个头部和一 个尾部,但是尾部的 "next" 指针指向头部的。对于这样一个模型,我们显然不需要同时保存指向头部和尾部的引用(指针) 。只要保存一个指向尾部的引用(指针),我们就总能通过尾部的 "next" 引用找到头部。
代码段 7-9 和代码段 7-10 给出了基于这个模型实现的循环队列类。该类只有两个实例变量:一个是_tail, 用于指向尾部节点的引用(当队列为空时指向 None) ;另一个是_size, 用于记录当前队列中元素的数量。当一个操作涉及队列的头部时,我们用 self._tail._next 标识队列的头部。当调用 enqueue 操作时,一个新的节点将被插入队列的尾部与当前头部之间,然后这个新节点变成了新的尾部。
除了传统的队列操作, CircularQueue 类还支持一个循环的方法,该方法可以更有效地实现删除队首的元素以及将该元素插入队列尾部这两个操作的合并处理。用循环来表示,简单地设self._tail = self._tail._next, 以使原来的头部变成新的尾部。(原来头部的后继节点成为新的头部)
from ..exceptions import Empty
class CircularQueue:
"""Queue implementation using circularly linked list for storage."""
#---------------------------------------------------------------------------------
# nested _Node class
class _Node:
"""Lightweight, nonpublic class for storing a singly linked node."""
__slots__ = '_element', '_next' # streamline memory usage
def __init__(self, element, next):
self._element = element
self._next = next
# end of _Node class
#---------------------------------------------------------------------------------
def __init__(self):
"""Create an empty queue."""
self._tail = None # will represent tail of queue
self._size = 0 # number of queue elements
def __len__(self):
"""Return the number of elements in the queue."""
return self._size
def is_empty(self):
"""Return True if the queue is empty."""
return self._size == 0
def first(self):
"""Return (but do not remove) the element at the front of the queue.
Raise Empty exception if the queue is empty.
"""
if self.is_empty():
raise Empty('Queue is empty')
head = self._tail._next
return head._element
def dequeue(self):
"""Remove and return the first element of the queue (i.e., FIFO).
Raise Empty exception if the queue is empty.
"""
if self.is_empty():
raise Empty('Queue is empty')
oldhead = self._tail._next
if self._size == 1: # removing only element
self._tail = None # queue becomes empty
else:
self._tail._next = oldhead._next # bypass the old head
self._size -= 1
return oldhead._element
def enqueue(self, e):
"""Add an element to the back of queue."""
newest = self._Node(e, None) # node will be new tail node
if self.is_empty():
newest._next = newest # initialize circularly
else:
newest._next = self._tail._next # new node points to head
self._tail._next = newest # old tail points to new node
self._tail = newest # new node becomes the tail
self._size += 1
def rotate(self):
"""Rotate front element to the back of the queue."""
if self._size > 0:
self._tail = self._tail._next # old head becomes new tail
7.3 双向链表¶
在单向链表中,每个节点为其后继节点维护一个引用。我们巳经说明了在管理一个序列的元素时如何使用这样的表示方法。然而,单向链表的不对称性产生了一些限制。在 7.1 节 的开头,我们强调过可以有效地向一个单向链表内部的任意位置插入一个节点,也可以在头部轻松地删除一个节点,但是不能有效地删除链表尾部的节点。更一般化的说法是,如果仅给定链表内部指向任意一个节点的引用,我们很难有效地删除该节点, 因为我们无法立即确定待删除节点的前驱节点(而且删除处理中该前驱节点需要更新它的 " next " 引用) 。
为了提供更好的对称性,我们定义了一个链表,每个节点都维护了指向其先驱节点以及后继节点的引用。这样的结构被称为双向链表。这些列表支持更多各种时间复杂度为 O(1) 的更新操作,这些更新操作包括在列表的任意位置插入和删除节点。我们会继续用 " next " 表示指向当前节点的后继节点的引用,并引入 " prev " 引用其前驱节点。
头哨兵和尾哨兵¶
在操作接近一个双向链表的边界时,为了避免一些特殊情况,在链表的两端都追加节点是很有用处的: 在列表的起始位置添加头节点( header ) ,在列表的结尾位置添加尾节点 ( tailer ) 。这些“特定”的节点被称为哨兵(或保安) 。这些节点中并不存储主序列的元素。
图 7-10 中给出了一个带哨兵的双向链表。
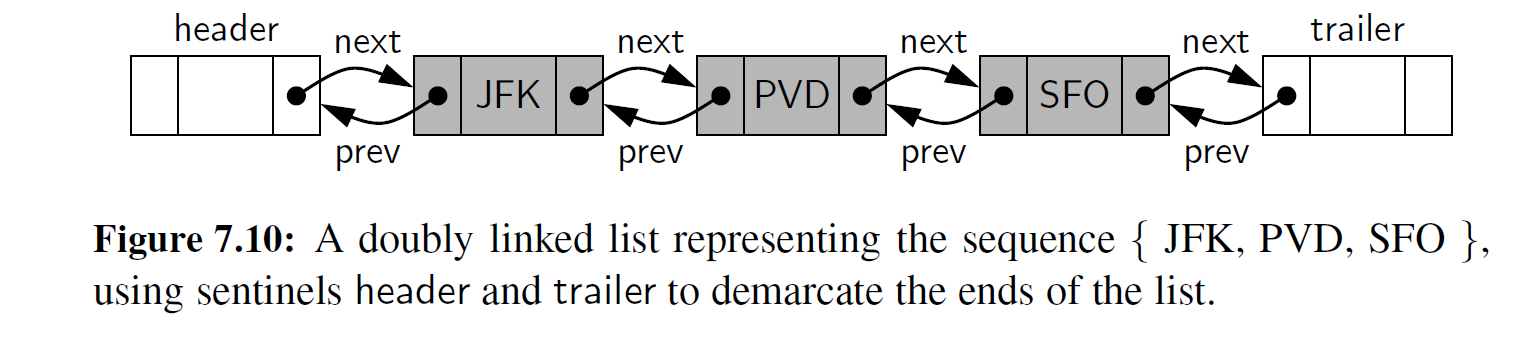
当使用哨兵节点时, 一个空链表需要初始化,使头节点的 " next " 域指向尾节点,并令尾节点的 " prev " 域指向头节点。哨兵节点的剩余域是无关紧要的。对于一个非空的列表, 头节点的 " next " 域将指向一个序列中第一个真正包含元素的节点,对应的尾节点的 " prev " 域指向这个序列中最后一个包含元素的节点
使用哨兵的优点¶
虽然不使用哨兵节点就可以实现双向链表(正如 7.1 节中的单向链表那样),但哨兵只占用很小的额外空间就能极大地简化操作的逻辑。最明显的是,头和尾节点从来不改变——只改变头节点和尾节点之间的节点。此外,可以用统一的方式处理所有插入节点操作, 因为一 个新节点总是被放在一对已知节点之间。类似地,每个待删除的元素都是确保被存储在前后都有邻居的节点中的。
相比之下,回顾 7.1.2 节中 LinkedQueue 的实现( 其入 enqueue 方法在代码段 7-8 中给出), 一个新节点是在列表的尾部进行添加的。然而,它需要设置一个条件去管理向空列表插入节点的特例情况。在一般情况下,新节点被连接在列表现在的尾部之后。但当插入空列表中时,不存在列表的尾部,因此必须重新给 self._head 赋值为新节点的引用。在实现中, 使用哨兵节点可以消除这种特例的处理,就好像在新节点之前总是有一个已存在的节点。
双端链表的插入和删除¶
向双向链表插入节点的每个操作都将发生在两个已有节点之间,如图 7-11 所示。例如, 当一个新元素被插在序列的前面时,我们可以简单地将这个新节点插入头节点和当前位于头节点之后的节点之间,如图 7-12 所示。
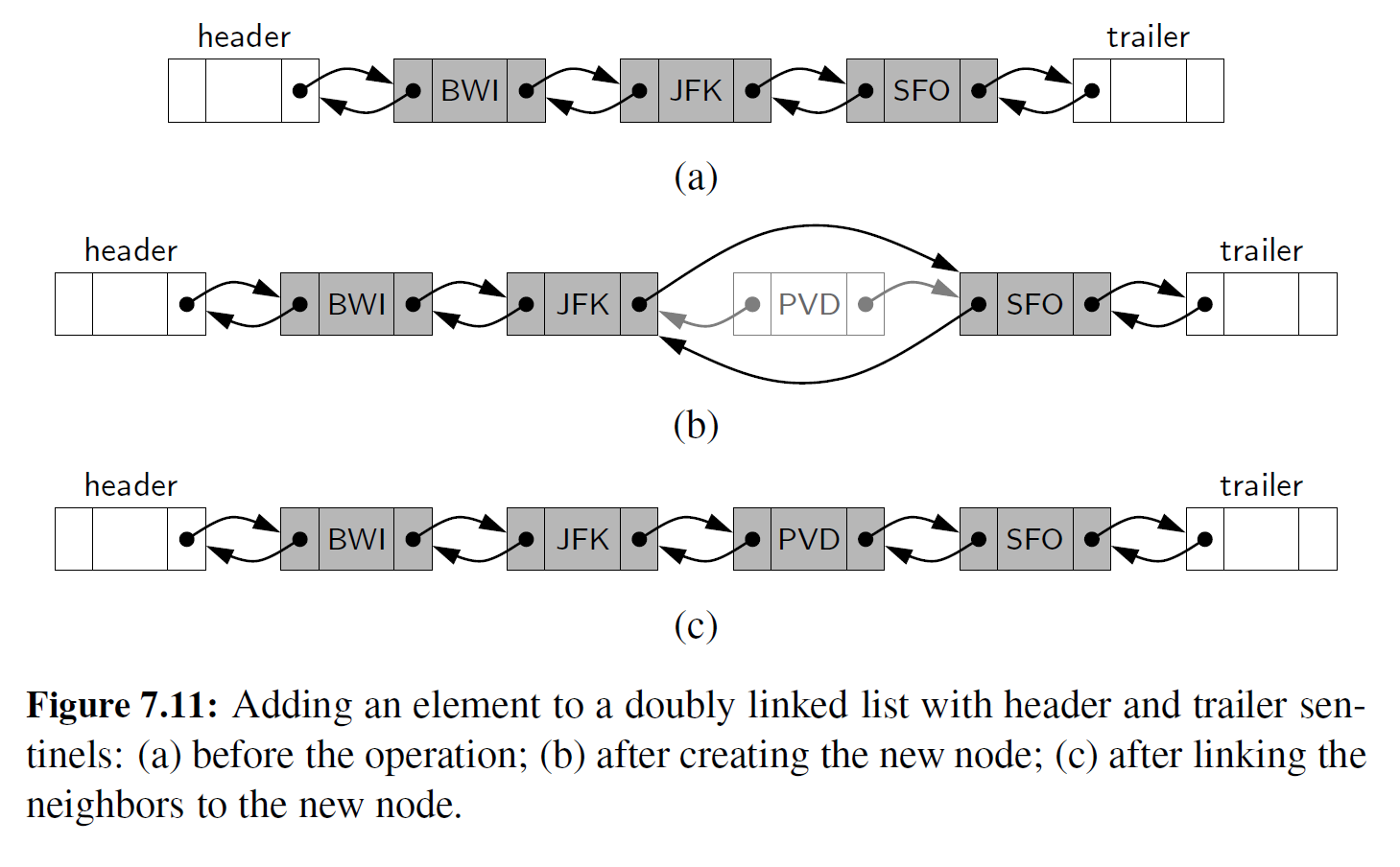
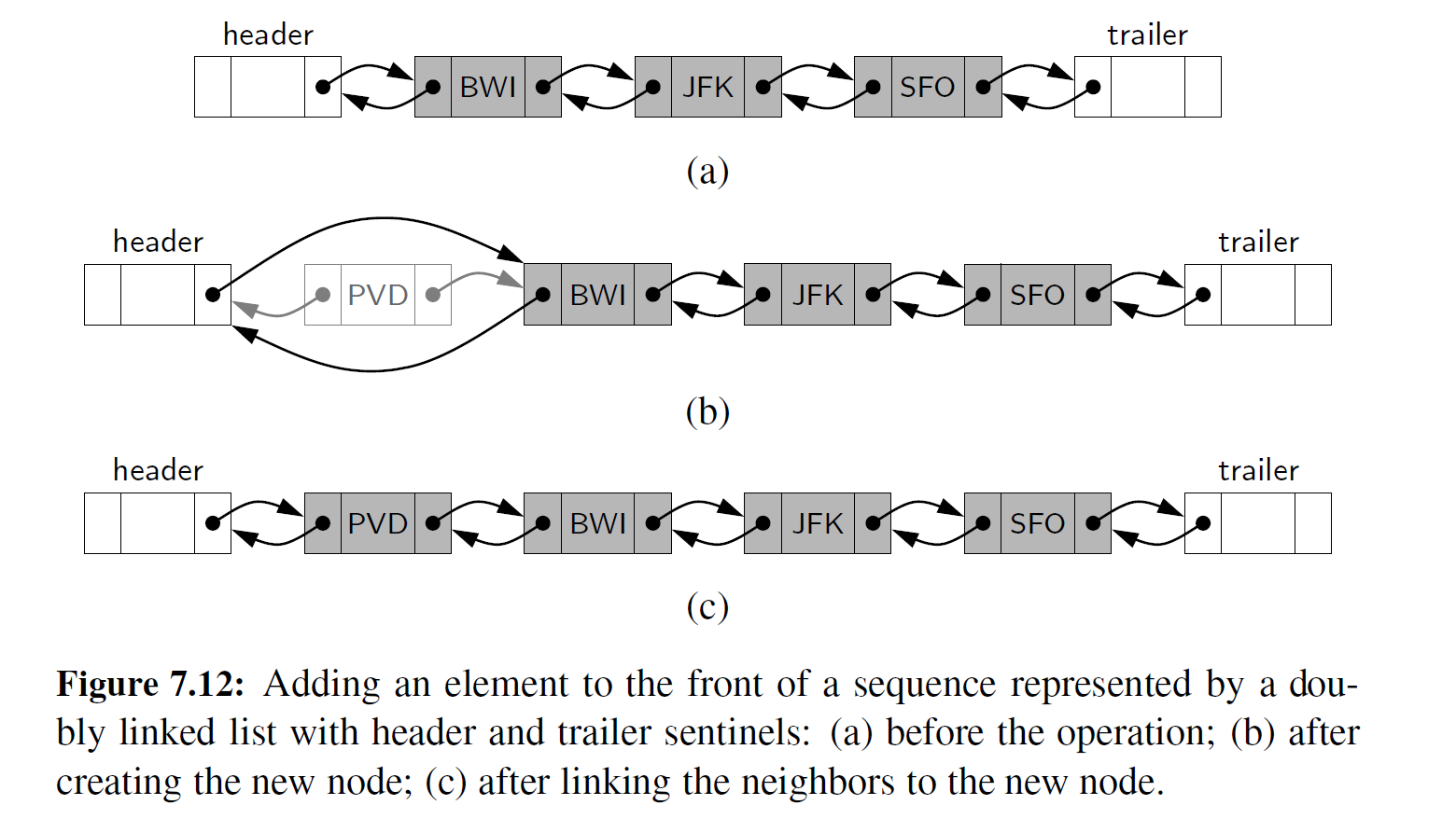
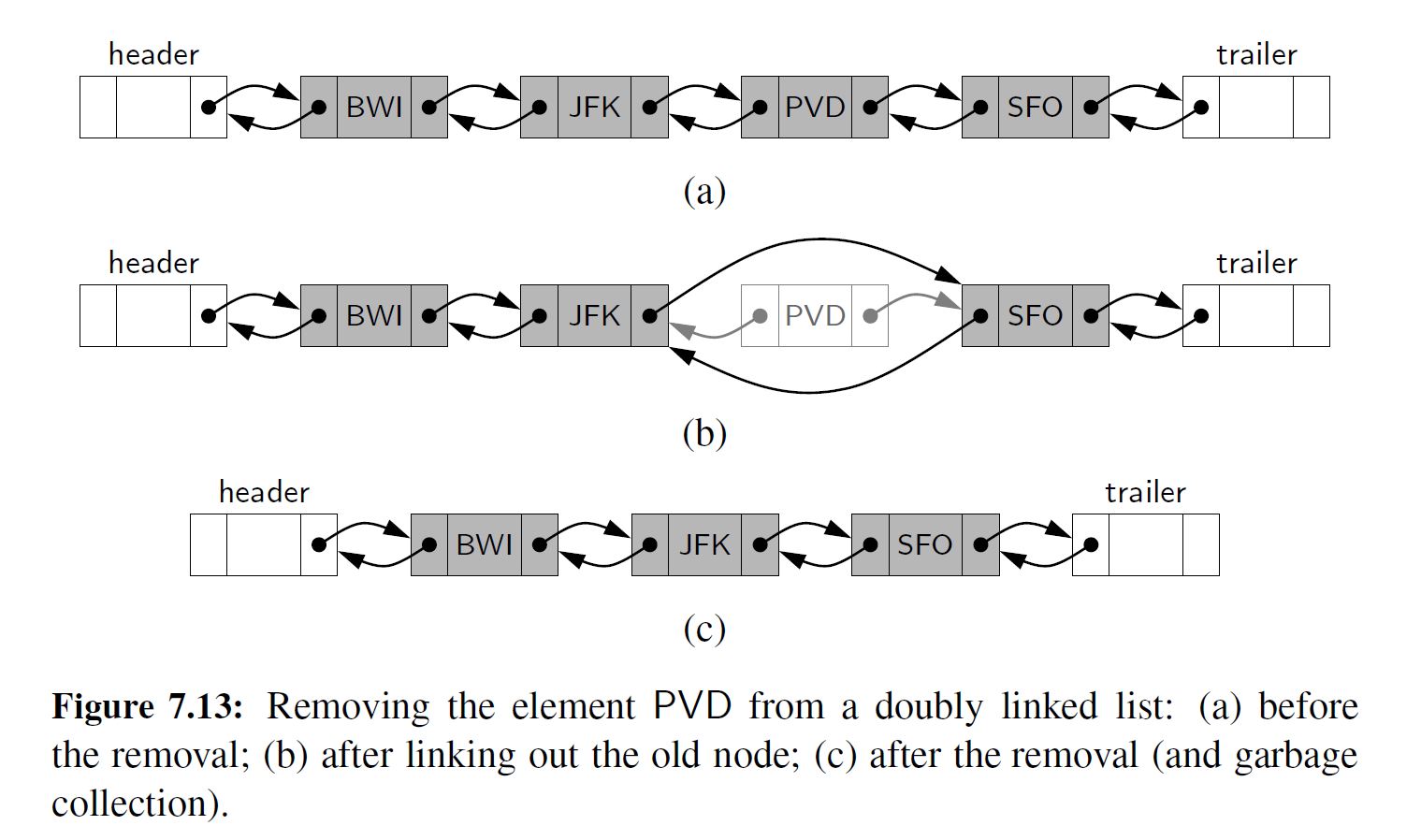
图 7-13 所示的是和插入相反的过程——删除节点。被删除节点的两个邻居直接相互连接起来,从而绕过被删节点。这样一来,该节点将不再被视作列表的一部分,它也可以被系统收回。由于用了哨兵、可以使用相同的方法实现删除序列中的第一个或最后一个元素. 因为一个元素必然存储在位于某两个已知节点之间的节点上。
7.3.1 双向链表的基本实现¶
我们首先给出一个双向链的初步实现,这个实现是在一个名为 _DoublyLinkedBase 的类中定义的。由于我们不打算为一般应用提供一个常规的公共接口,因此有意将这个类名定义为以下划线开头。我们会看到链表可以支持一般在最坏情况下时间复杂度为 O(1) 的插入和删除,但这仅限于当一个操作的位置可以被简单地识别出来的情况。对于基于数组的序列, 用整数作为索引是描述序列中某个位置的一种便利之法。然而, 当没有给出一种有效的方法来查找一个链表中的第 j 个元素时,索引并不是合适的方法,因为这种方法将需要遍历链表 的一部分。
当处理一个链表时,描述一个操作的位置最直接的方法是找到与这个列表相关联的节点。但是,我们倾向于将数据结构的内部处理封装起来,从而避免用户直接访问到列表的节点。在本章的剩余部分,我们将开发两个从_DoublyLinkedBase 类继承而来的公有类,从而提供更一致的概念。尤其是在 7.3.2 节中,我们将提供一个 LinkedDeque 类,用于实现在 6.3 节中介绍的双头队列 ADT 。这个类只支持在队列末端的操作,所以用户不需要查找其在内部列表中的位置。在 7.4 节中,我们将引入一个新的概念 PositonaList , 这个类提供一个公共接口,以允许从一个列表中任意插入和删除节点。
低级_DoublyLinkedBase 类使用一个非公有的节点类_Node, 这个非公有类类似于一个单向链表。如代码段 7-4 给出的,这个双向链表的版本除了包括_prev 属性,还包含_next 和_element属性,如代码段 7-1 所示。
class _Node:
"""Lightweight, nonpublic class for storing a doubly linked node."""
__slots__ = '_element', '_prev', '_next' # streamline memory
def __init__(self, element, prev, next): # initialize node's fields
self._element = element # user's element
self._prev = prev # previous node reference
self._next = next # next node reference
_DoublyLinkBase 类中定义的其余内容在代码段 7-12 中给出。构造函数实例化两个哨兵节点并将这两个节点直接链接。我们维护了一个_size 成员以及公有成员 __len__ 和 is_ empty, 以使这些行为可以直接被子类继承。
class _DoublyLinkedBase:
"""A base class providing a doubly linked list representation."""
def __init__(self):
"""Create an empty list."""
self._header = self._Node(None, None, None)
self._trailer = self._Node(None, None, None)
self._header._next = self._trailer # trailer is after header
self._trailer._prev = self._header # header is before trailer
self._size = 0 # number of elements
#-------------------------- public accessors --------------------------
def __len__(self):
"""Return the number of elements in the list."""
return self._size
def is_empty(self):
"""Return True if list is empty."""
return self._size == 0
#-------------------------- nonpublic utilities --------------------------
def _insert_between(self, e, predecessor, successor):
"""Add element e between two existing nodes and return new node."""
newest = self._Node(e, predecessor, successor) # linked to neighbors
predecessor._next = newest
successor._prev = newest
self._size += 1
return newest
def _delete_node(self, node):
"""Delete nonsentinel node from the list and return its element."""
predecessor = node._prev
successor = node._next
predecessor._next = successor
successor._prev = predecessor
self._size -= 1
element = node._element # record deleted element
node._prev = node._next = node._element = None # deprecate node
return element # return deleted element
这个类的其他两个方法是私有的应用程序,即_insert_between 和_delete_node 。这些方法分别为插入和删除提供通用的支待,但需要以一个或多个节点的引用作为参数。_insert_ between 方法是根据图 7-11 所示的算法模型化实现的。该方法创建一个新节点,节点字段初始化链接到指定的邻近节点,然后邻近节点的字段要进行更新,以获得最新节点的相关信息。为后继处理方便,这个方法返回新创建的节点的引用。
_delete_node 方法是根据图 7-13 所示的算法模块化进行实现的。与被删除节点相邻的两个点, 直接相链接,从而使列表绕过这个被删除节点,作为一种形式,我们故意重新设置被删除节点的_prev 、_next 和_element 域为空(在记录要返回的元素之后) 。虽然被删除的节点会被列表的其余部分忽略,但设置该节点的域为 none 是有利的,这样一来,该节点与其他节点不必要的链接和存储元素将会被消除,从而帮助 python 进行垃圾回收。我们还将依赖这个配置识别为因不再是列表的一部分而“被弃用”的节点。
7.3.2 用双向链表实现双端队列¶
6.3 节中介绍了双端队列 ADT 。由于偶尔需要调整数组的大小,我们基于数组实现的所有操作都在平均 O(1) 的时间复杂度下得以完成。在一个基于双向链表的实现中,我们能够在最坏情况下以时间复杂度为 O(1) 完成双端队列的所有操作。
代码段 7-13 给出了 LinkedDeque 类的实现,它继承自前一节中介绍的双端队列 _ DoublyLinkedBase 类。由于 LinkedDeque 类中的一系列继承方法就可以初始化一个新的实例,所以我们不再提供一个明确的方法来初始化链式队列类。我们还借助于__len__和 is_ empty 等继承而得的方法来满足双端队列 ADT 的要求。
from .doubly_linked_base import _DoublyLinkedBase
from ..exceptions import Empty
class LinkedDeque(_DoublyLinkedBase): # note the use of inheritance
"""Double-ended queue implementation based on a doubly linked list."""
def first(self):
"""Return (but do not remove) the element at the front of the deque.
Raise Empty exception if the deque is empty.
"""
if self.is_empty():
raise Empty("Deque is empty")
return self._header._next._element # real item just after header
def last(self):
"""Return (but do not remove) the element at the back of the deque.
Raise Empty exception if the deque is empty.
"""
if self.is_empty():
raise Empty("Deque is empty")
return self._trailer._prev._element # real item just before trailer
def insert_first(self, e):
"""Add an element to the front of the deque."""
self._insert_between(e, self._header, self._header._next) # after header
def insert_last(self, e):
"""Add an element to the back of the deque."""
self._insert_between(e, self._trailer._prev, self._trailer) # before trailer
def delete_first(self):
"""Remove and return the element from the front of the deque.
Raise Empty exception if the deque is empty.
"""
if self.is_empty():
raise Empty("Deque is empty")
return self._delete_node(self._header._next) # use inherited method
def delete_last(self):
"""Remove and return the element from the back of the deque.
Raise Empty exception if the deque is empty.
"""
if self.is_empty():
raise Empty("Deque is empty")
return self._delete_node(self._trailer._prev) # use inherited method
在使用哨兵时,实现方法的关键是要记住双端队列的第一个元素并不存储在头节点,而是存储在头节点后的第一个节点(假定双端队列是非空的) 。同样,尾节点之前的一个节点中存储的是双端队列的最后一个元素。
我们使用通过继承得到的方法_insert between 向双端队列的两端进行插入操作。为了向双端队列前端插入一个元素,我们需要将这个元素立即插入头节点和其后的一个节点之间。如果是在双端队列末尾插入节点,则可直接将节点置于尾节点之前。值得注意的是,这些操 作即使在双端队列为空时也能成功:在这种情况下,新节点将被放置在两个哨兵之间。当从 一个非空队列删除一个元素,且明确知道目标节点肯定有前驱和后继节点时,我们可以利用继承得到的_delete_node 方法来实现
7.4 位置列表的抽象数据类型¶
到目前为止,我们所讨论的抽象数据类型包括栈、队列和双向队列等,并且仅允许在序列的一端进行更新操作。有时,我们希望有一个更一般的概念。例如,虽然我们采用队列的 FIFO 语义作为一种模型,来描述正在等待与客户服务代表对话的顾客或者正在排队买演出门票的粉丝,但是队列 ADT 有很大的局限。如果等待的顾客在到达顾客服务队列列首之前决定离开,或者排队买票的人允许他的朋友"插队”到他所站的位置呢?我们希望能够设计一个抽象数据类型来为用户提供一种可以定位到序列中任何元素的方法,并且能够执行任意的插入和删除操作。
在处理基于数组的序列(如 python 列表)时,整数索引提供了一种很好的方式来描述一个元素的位置,或者描述一个即将发生插入和删除操作的位置。然而,数字索引并不适用于描述一个链表内部的位置,因为我们不能有效地访问一个只知道其索引的条目。找到链表中一个给定索引的元素,需要从链表的开始或者结束的位置起逐个遍历从而计算出目标元素的位置。
此外,在描述某些应用程序中的本地位置时,索引并非好的抽象,因为序列中不停地发生插入或删除操作,条目的索引值会随着时间的推移发生变化。例如, 一个排队者的具体位置并不能通过精确地知道队列中在他之前到底有多少人而很容易地描述出来。我们提出一个抽象, 如图 7-14 所示,用一些其他方法描述位置。然后我们希望给一些情况建模,例如,当一个指定的排队者在到达队首之前离开队列,或立即在队列中一个指定的排队者之后增加一个新人。
再如,一个文本文档可以被视为一个长的字符序列。文字处理器使用游标这一抽象类型来描述文档中的一个位置,而没有明确地使用整数索引,支持如"删除此游标处的字符 ” 或者 ” 在当前游标之后插入新的字符 ” 这样的操作。此外,我们可以引用文档中一个固有的位置,比如一个特定章节的开始,但不能依赖于一个字符索引(甚至一个章节编号),因为这个索引可能会随着文档的演化而改变
节点的引用表示位置¶
链表结构的好处之一是:只要给出列表相关节点的引用,它可以实现在列表的任意位置执行插入和删除操作的时间复杂度都是 O(1) 。因此,很容易开发一个 ADT, 它以一个节点引用实现描述位置的机制。事实上, 7.3.1 节_DoublyLinkedBase 基础类中的_insert between 和_delete node方法都接受节点引用作为参数。
然而,这样直接使用节点的方式违反了在第 2 章中介绍的抽象和封装这两个面向对象的设计原则。为了我们自己和抽象的用户的利益,有几个原因致使我们倾向于封装一个链表中的节点:
- 对于用户来说,如果不被数据结构的实现中那些例如节点的低级操作, 或依赖哨兵节点的使用等不必要的细节所干扰,那么使用这些数据结构会更加简单。注意,在 _ DoubleyLinkedBased 类中使用_insert between 方法来向一个序列的起始位置添加节点时,头部哨兵必须作为参数传递进去。
- 如果不允许用户直接访问或操作节点,我们可以提供一个更健壮的数据结构。这样就可以确保用户不会因无效管理节点的连接而致使列表的一致性变成无效。如果允许用户调用我们定义的
_DoubleyLinkedBased类中的_insert between或delete node方法,并将一个不属于给定列表的节点作为参数传递进去,则会发生更微妙的问题 (回头看看这段代码, 看看为什么它会引起这个问题) 。 - 通过更好地封装实施的内部细节,我们可以获得更大的灵活性来重新设计数据结构以及改善性能。事实上,通过一个设计良好的抽象,我们可以提供一个非数字的位置的概念,即使使用一个基于数组的序列。
由于这些原因,我们引入一个独立的位置抽象表示列表中一个元素的位置,而不是直接依赖于节点,进而引入一个可以封装双向链表的(甚至是基于数组序列的, 参见练习 P-7.46 ) 完整的含位置信息的列表 ADT
7.4.1 含位置信息的列表抽象数据类型¶
为了给具有标识元素位置能力的元素序列提供一般化抽象,我们定义了一个含位置信息的列表 ADT 以及一个更简单的位置抽象数据类型,来描述列表中的某个位置。将一个位置作为更广泛的位置列表中的一个标志或标记。改变列表的其他位置不会影响位置 p 。使一个 位置变得无效的唯一方法就是直接显式地发出一个命令来删除它。
位置实例是一个简单的对象,只支持以下方法:
p.element():返回存储在位置 p 的元素
在位置列表 ADT 中,位置可以充当一些方法的参数或是作为其他方法的返回值。在描述位置列表的行为时,我们介绍如下列表 L 所支持的访问器方法:
-
L.first():返回 L 中第一个元素的位置。如果 L 为空,则返回 None 。 -
L.last():返回 L 中最后一个元素的位置。如果 L 为空,则返回 None. -
L.before(p):返回 L 中 p 紧邻的前面元素的位置。如果 p 为第一个位置, 则返回 None 。 -
L.after(p):返回 L 中 p 紧邻的后面元素的位置。如果 p 为最后一个位置,则返回 None 。 -
L.is_empty(): 如果 L 列表不包含任何元素,返回 True 。 -
len(L): 返回列表元素的个数。 -
iter(L): 返回列表元素的前向迭代器。见 1.8 节中有关 python 迭代器的讨论。
位置列表 A DT 也包括以下更新方法:
-
L.add_first(e):在 L 的前面插入新元素 e, 返回新元素的位置。 -
L.add_last(e):在 L 的后面插入新元素 e, 返回新元素的位置。 -
L.add_before(p, e):在 L 中位置 p 之前插入一个新元素 e, 返回新元素的位置。 -
L.add_after(p, e):在 L 中位置 p 之后插入一个新元素 e, 返回新元素的位置。 -
L.replace(p, e): 用元素 e 取代位置 p 处的元素,返回之前 p 位置处的元素。 -
L.delete(p): 删除并且返回 L 中位置 p 处的元素,取消该位置。
ADT 的这些方法以参数形式接收 p 的位置,如果列表 L 中 p 不是有效的位置信息,则发生错误。
注意,含位置信息列表 ADT 中 frist() 和 last() 方法的返回值是相关的位置,不是元素 (这一点与双向队列中相应的 frist() 和last() 的方法相反) 。含位置信息列表的第一个元素可以通过随后调用这个位置上的元素的方法来确定,即 L.first().element() 。将位置作为返回值来接收的优势是我们可以使用这个位置为列表导航。例如,下面代码片段将打印一个名为 data 的含位置信息列表的所有元素。
cursor = data.first( )
while cursor is not None:
print(cursor.element( )) # print the element stored at the position
cursor = data.after(cursor) # advance to the next position (if any)
上述代码依赖于这样的规定,在对列表最后面的位置调用 “after" 时,就会返回 None 对象。这个返回值可以明确地从所有合法位置区分出来。类似地, 这个含位置信息的列表 ADT 在对列表最前面的位置调用 “before" 方法时返回值为 None, 或者在空列表调用 frist 和 last 方法时,也会返回 None 。因此,即使列表为空,上面的代码片段也可正常运行。
因为这个 ADT 包括支持 python 的 iter 函数。用户可以采用传统的 for 循环语法向前遍历这样一个命名数据列表
for e in data:
print(e)
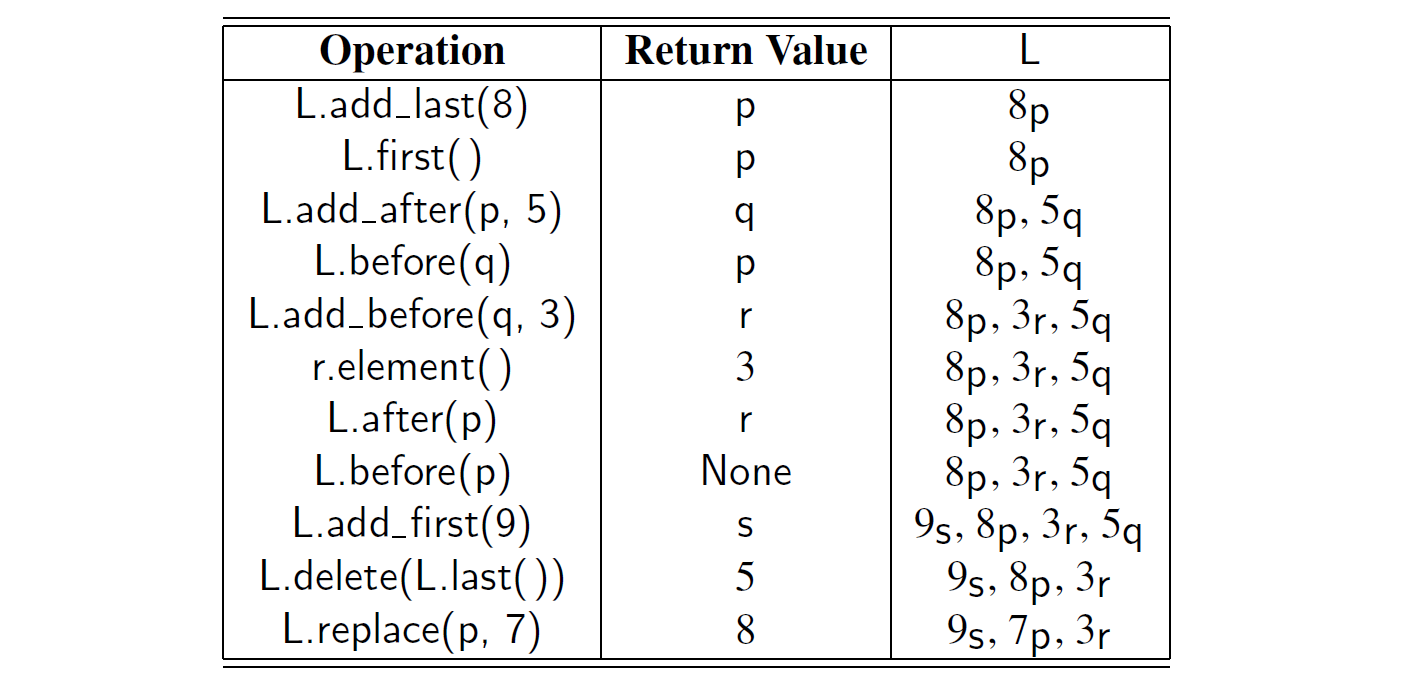
位置列表 ADT 更为一般化的引导和更新方法如下面示例所示。
例题 7-1 :下表显示了一个初始化为空的位置列表 L 上的一些列操作。为了区分位置实例,我们使用了变量 p 和 q 。为了便于展示,当展示列表内容时,我们使用下标符号来表示它的位置。
7.4.2 双向链表实现¶
在本节中,我们呈现一个使用双向链表完整实现位置列表类 PositionalList 的方法,并满足以下重要的命题。
命题 7-2: 当使用双向链表实现时,位置列表 ADT 每个方法的运行时间在最坏情况下是 O(1) 。
我们依靠第 7.3.1 节中的 DoublyLinkedBase 类来进行低级表示; 新类的主要职责是根据位置列表 ADT 提供公共接口。 我们在代码片段 7.14 中以嵌套在我们的 PositionalList 类中的公共 Position 类的定义开始我们的类定义。 Position 实例将用于表示列表中元素的位置。 我们的各种 PositionalList 方法可能最终会创建引用相同底层节点的冗余 Position 实例(例如,当 first 和 last 相同时)。 出于这个原因,我们的 Position 类定义了 __eq__ 和 __ne__ 特殊方法,以便当两个位置引用同一节点时,诸如 p == q 的测试评估为 True。
确认位置¶
每当 PositionalList 类的一个方法以参数形式接收一个位置信息时, 我们想确认这个位置是有效的, 以确定与这个位置关联的底层的节点。这个功能是由一个名叫_validate 的非公有的方法实现的。在内部, 一个位置为链表的相关节点维护着引用信息,并且列表实例的 引用包含指定的节点。利用这种容器的引用,当调用者发送不属于指定列表的位置实例时,我们可以轻易地检测到。
我们也能够检测到一个属于列表,但其指向节点不再是列表一部分的位置实例。回想基类的 _delete_node 将被删除节点的前驱和后继的引用设置为 None; 我们可以通过识别这一条件来检测被弃用的节点。
访问和更新方法¶
Positona 类的访问方法在代码段 7-15 中给出,更新方法在代码段 7-16 中给出。所有这些方法非常适用于底层双向链表实现支持位置列表 ADT 的公共接口。这些方法依赖于 _ validate 工具 “打开“ 发送的任何位置。它们还依赖于一个_make_position 工具来“包装” 节点作为 Position 实例返回给用户,确保不要返回一个引用哨兵的位置。为了方便起见,我们已经重载了继承的实用程序方法中的—insert_between 方法,这样可以返回一个相对应的新创建节点的位置(继承版本则返回节点本身) 。
抛弃使用 1,2,3……这样的编号(或者说位置)表示法,在这里我们为链表中的每一个元素都配备了一个对应的 Position 实例,并且在构建这个数据结构时使用
__iter__让其变得可以被迭代,从而达到与数组编号同样的效果
from .doubly_linked_base import _DoublyLinkedBase
class PositionalList(_DoublyLinkedBase):
"""A sequential container of elements allowing positional access."""
#-------------------------- nested Position class --------------------------
class Position:
"""An abstraction representing the location of a single element.
Note that two position instaces may represent the same inherent
location in the list. Therefore, users should always rely on
syntax 'p == q' rather than 'p is q' when testing equivalence of
positions.
"""
def __init__(self, container, node):
"""Constructor should not be invoked by user."""
self._container = container
self._node = node
def element(self):
"""Return the element stored at this Position."""
return self._node._element
def __eq__(self, other):
"""Return True if other is a Position representing the same location."""
return type(other) is type(self) and other._node is self._node
def __ne__(self, other):
"""Return True if other does not represent the same location."""
return not (self == other) # opposite of __eq__
#------------------------------- utility methods -------------------------------
def _validate(self, p):
"""Return position's node, or raise appropriate error if invalid."""
if not isinstance(p, self.Position):
raise TypeError('p must be proper Position type')
if p._container is not self:
raise ValueError('p does not belong to this container')
if p._node._next is None: # convention for deprecated nodes
raise ValueError('p is no longer valid')
return p._node
def _make_position(self, node):
"""Return Position instance for given node (or None if sentinel)."""
if node is self._header or node is self._trailer:
return None # boundary violation
else:
return self.Position(self, node) # legitimate position
#------------------------------- accessors -------------------------------
def first(self):
"""Return the first Position in the list (or None if list is empty)."""
return self._make_position(self._header._next)
def last(self):
"""Return the last Position in the list (or None if list is empty)."""
return self._make_position(self._trailer._prev)
def before(self, p):
"""Return the Position just before Position p (or None if p is first)."""
node = self._validate(p)
return self._make_position(node._prev)
def after(self, p):
"""Return the Position just after Position p (or None if p is last)."""
node = self._validate(p)
return self._make_position(node._next)
def __iter__(self):
"""Generate a forward iteration of the elements of the list."""
cursor = self.first()
while cursor is not None:
yield cursor.element()
cursor = self.after(cursor)
#------------------------------- mutators -------------------------------
# override inherited version to return Position, rather than Node
def _insert_between(self, e, predecessor, successor):
"""Add element between existing nodes and return new Position."""
node = super()._insert_between(e, predecessor, successor)
return self._make_position(node)
def add_first(self, e):
"""Insert element e at the front of the list and return new Position."""
return self._insert_between(e, self._header, self._header._next)
def add_last(self, e):
"""Insert element e at the back of the list and return new Position."""
return self._insert_between(e, self._trailer._prev, self._trailer)
def add_before(self, p, e):
"""Insert element e into list before Position p and return new Position."""
original = self._validate(p)
return self._insert_between(e, original._prev, original)
def add_after(self, p, e):
"""Insert element e into list after Position p and return new Position."""
original = self._validate(p)
return self._insert_between(e, original, original._next)
def delete(self, p):
"""Remove and return the element at Position p."""
original = self._validate(p)
return self._delete_node(original) # inherited method returns element
def replace(self, p, e):
"""Replace the element at Position p with e.
Return the element formerly at Position p.
"""
original = self._validate(p)
old_value = original._element # temporarily store old element
original._element = e # replace with new element
return old_value # return the old element value
yield函数在 python 中,使用了
yield函数的类被称为生成器,其特点是可以被循环语句迭代循环语句的迭代方法许下:
- 输入一个可以迭代的数据类型(比如 list )
- 进行一次操作,碰到类中的
yield语句则执行该语句然后暂停,直到下一个next()命令1. yield 的核心目的:為了節省記憶體¶
如果想要印出 0~100 的平方時,我們可能會這樣寫。
powers = [x**2 for x in range(100)] for x in powers: print(x)但這樣有一個致命問題在於,必須把整個 list 都存放在記憶體中,100 個元素可能還不成問題,但如果今天的對象是一百萬筆資料,記憶體可能會承受不了,程式就崩潰了。
接下來就會說明 yield 要如何節省記憶體,但在此之前,先來談談 python 的生成器(generator)。
2. 什麼是生成器(generator)?¶
生成器是一個可迭代的物件,可以放在 for 迴圈的 in 前面,或者使用 next()函數呼叫執行下一次迭代。
和列表的差別在於,生成器會保存上次紀錄,並只有在呼叫下一層迭代的時候才載入記憶體執行。
所以將上面的例子改寫成生成器,結果是一樣的,卻可以防止超過記憶體,注意我用的是
(而不是[。powers = (x**2 for x in range(100)) for x in powers: print(x)3. 函數加入 yield 後不再是一般的函數,而被視作為生成器(generator)¶
呼叫函數後,回傳的並非數值,而是函數的生成器物件。
4. yield 和 return 一樣會回傳值,不過 yield 會記住上次執行的位置¶
yield 和 return 一樣都會回傳值並中斷在目前位置,但最大不同在於 yield 在下次迭代時會從上次迭代的下一行接續執行,一直執行到下一個 yield 出現,如果沒有下一個 yield 則結束這個生成器。而且接續上一個迭代前的變數不會改變,就是維持上次結束前的模樣。
這部分我們來看下面這個例子:
def yield_test(n): print("start n =", n) for i in range(n): yield i*i print("i =", i) print("end") tests = yield_test(5) for test in tests: print("test =", test) print("--------")執行結果:
start n = 5 test = 0 -------- i = 0 test = 1 -------- i = 1 test = 4 -------- i = 2 test = 9 -------- i = 3 test = 16 -------- i = 4 end
- 從第 10、11 行看到呼叫 yield_test()後回傳的不是一個數值,而是一個可迭代的生成器。
- 在第一次迭代時,印出了 "start n = 5",因為不在迴圈中,所以僅僅印出這一次。
- 進入迴圈中,第一次時 i=0,接著遇到 yield 並回傳 0*0 = 0,並回到主程序。
- 主程序的 test 接收到回傳的 0,於是印出 "test = 0" 並印出 "--------",結束這次迭代。
- 接著進行第二次迭代,會從上次結束的下一行開始,因此印出 "i = 0"。
- 完成後又回到迴圈開始,這時 i=1,接著再次遇到 yield 並回傳 1*1 = 1,並回到主程序。
- 主程序的 test 接收到回傳的 1,於是印出 "test = 1" 並印出 "--------",結束這次迭代。
- 其他次迭代依此類推,直到 i=5 跳出迴圈,印出 "end" 之後已經沒有 yield 了,生成器會返回一個 error
StopIteration(這邊沒有印出來),告訴主程序迭代已經結束了。- 結束主程序。
看完上面例子後,應該會從原本朦朦朧朧到有點概念了吧,其實 yield 有點像偵錯模式的中斷點,只是多了中斷時回傳值而已。
5. next()呼叫下一次迭代,send(n)呼叫下一次迭代並傳遞參數¶
def test(): print("start...") while True: throw = yield 10 print("throw:", throw) p = test() print(next(p)) print("-----------") print(next(p)) print("-----------") print(g.send(7)) print("-----------")執行結果:
start... 10 ----------- throw: None 10 ----------- throw: 7 10 -----------
- 建立一個可迭代生成器 p。
- next()執行第一次迭代,印出 "start..." 並回傳 10,但注意 throw 在賦予值之前就被中斷了。
- next()執行第二次迭代,因為 throw 並沒有被沒有被賦予值,所以印出 "throw: None",接著回傳 10。
- send()傳入 7,等同於在上次結束的位置填入 7,因此 throw=7,印出 "throw: 7"。
順帶一提,第一次迭代不可以 send 任何數值進去,因為沒有上一個位置可以接收。
6. python range 小知識¶
在 python 2.X 中,有分 range 和 xrange 兩種,range 就像第一個例子,生成一個[0, 1, 2, ...]的 list。xrange 則像第二種例子,使用生成器減少記憶體消耗。
但在 python 3.X 後 range 就等於 xrange,使用 type()檢查會知道已經是 range 型態了。
print(type(range(10))) # <class 'range'>如果開始學就是 python3.X,就不必在意這些細節,繼續放心地用 range 吧!
7.5 位置列表的排序¶
在 5.5.2 节中,我们介绍了在一个基于数组的序列中的插入排序算法。在本节中,我们 开发一个在 PositionalList 上进行操作的实现,这 个实现同样是依赖于在对元素进行排序并不断增长的集合中实现的高级算法。
我们维护一个名为 marker 的变量, 这个变量表示一个列表当前排序部分最右边的位置。我们每次考虑用 pivot 标记 marker 刚过去的位置和 pivot 的元素属于相对排序的部分。我们使用另一个被命名为 walk 的变量,从 marker 向左移动,只要还有一个前驱元素的值大于 pivot 元素的值,就一直移动。这些变量的典型配置如图 7-15 所示。采用 python 对这个策略的实现如代码段 7-17 所示。
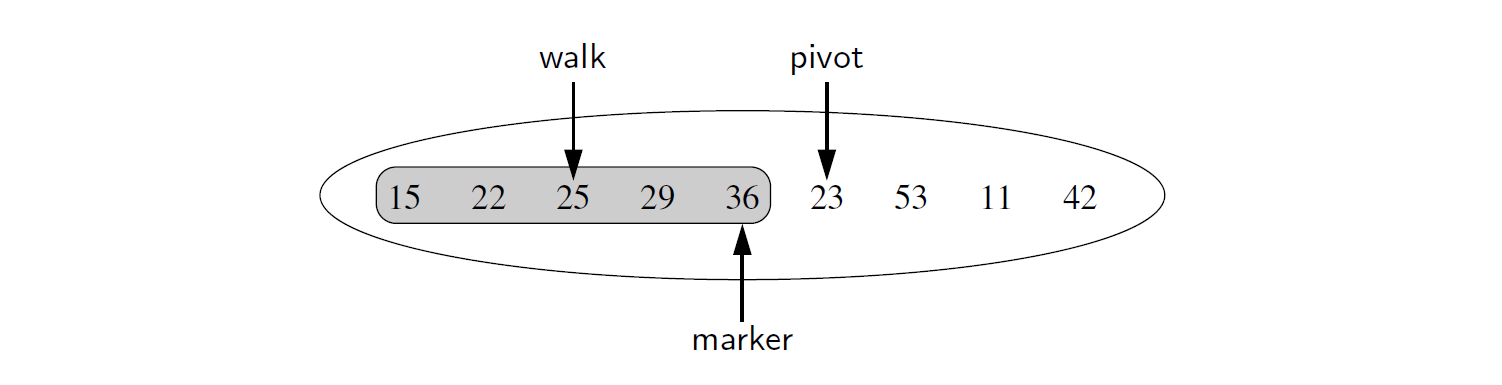
图 7-15 插入排序中一个步骤的示意图。阴影部分的元素(一直到 marker ) 已经排好序。在这一步中. pivot 的元素应该在 walk 位置之前被立即重新定位
def insertion_sort(L):
"""Sort PositionalList of comparable elements into nondecreasing order."""
if len(L) > 1: # otherwise, no need to sort it
marker = L.first()
while marker != L.last():
pivot = L.after(marker) # next item to place
value = pivot.element()
if value > marker.element(): # pivot is already sorted
marker = pivot # pivot becomes new marker
else: # must relocate pivot
walk = marker # find leftmost item greater than value
while walk != L.first() and L.before(walk).element() > value:
walk = L.before(walk)
L.delete(pivot)
L.add_before(walk, value) # reinsert value before walk
该算法的主要思想
- marker 从左边第一个变量开始,其后的第一个变量被命名为 pivot,如果 pivot 的值大于 marker,符合要求,将 pivot 变为 marker 进入下一次判断
- 如果 pivot 比 marker 小,那么此时生成一个变量 walk 向已经排序过的数中寻找一个前一个数比 pivot 小但后一个数比 pivot 大的位置,然后从链表中删除 pivot,在该位置中重新生成一个与 pivot 值相等的元素(依赖于 ADT PositionList)
7.6 案例研究:维护访问频率¶
在很多设置中,位置列表 ADT 都是有用的。例如,在一个模拟纸牌游戏的程序中,可以对每个人的手用位置列表进行建模(练习 P-7.47 ) 。因为大多数人会把相同花色的纸牌放在一起,所以从一个人手中插入和拿出纸牌可以使用位置列表 ADT 的方法实现,其位置是由各个花色的自然顺序决定的。同样, 一个简单的文本编辑器嵌入含位置的插入和删除的概念,因为这类编辑器的所有更新都是相对于一个游标执行的,该游标表示列表文本中正在被编辑的当前位置的字符。
在本节中,当跟踪每个元素被访问的次数时,我们考虑维护一个元素的集合。保存元素的访问数量,使我们知道集合中的哪些元素是最受欢迎的。这种场景的例子包括能够跟踪用户访问最多的 URL 信息的 Web 浏览器,或者是那种能够保存用户最常播放歌曲列表的音乐收藏夹。我们用新的 favorites list ADT 来建模,它支待 len 和 is_empty 方法,还支持以下的方法:
- access(e) :访间元素 e, 增加其访问数量。如果它尚未存在于收藏夹列表中,会将它添加至列表中。
- remove(e) :从收藏夹列表中移除元素 e, 前提是存在这样的 e 。
- top(k) :返回前 k 个访问最多的元素的迭代器。
7.6.1 使用有序表¶
管理收藏夹的第一种方法是在链表中存储元素, 按访问次数的降序顺序来存储这些元素。在访间或者移除一个元素时,通过从最经常访问的到最少经常访问的元素的方式查询列表的方法进行元素定位。返回前 k 个访问最频繁的元素很容易,因为只要返回列表中的前 k 个元素记录即可。
为了使列表以元素访问次数降序排列的方式保持不变,我们必须考虑一个单次访问操 对元素的排列顺序会产生怎样的影响。被访问的元素的访问次数加一,它的访问次数就可能 比原来在它之前的一个或者几个元素的都多了,这样就会破坏了列表的不变性。
所幸,我们可以采用前一节中介绍的一个类似于单向插入排序算法对列表重新排序。我们可以从访问数量增加的元素的位置开始,执行一个列表的向后遍历, 直至找到一个元素可以被重定位的有效位置之后。
使用组合模式¶
我们希望利用 PositionalList 类作为存储辅助实现一个收藏夹列表。如果位置列表的元素是收藏夹的简单元素,我们将面临的挑战是当列表的内容被重新排序时,维护访问次数以及保持列表中相关联元素的适当数量。我们使用一个通用的面向对象的设计模式——组合模式。
在这个模式中,我们定义了一个由两个或两个以上其他对象组成的单一对象。具体地说,我们定义了一个名为_Item 的非公有嵌套类,用于存储元素并以其访问次数作为一个实例。然后,将收藏夹作为 item 实例以 PositionalList 来维护,这样用户元素的访问次数就都可以被嵌入我们的表示方法中( _Item 从来不会暴露给 FavoritesList 的用户,见代码段 7-18 和 7- 19)
from .positional_list import PositionalList
class FavoritesList:
"""List of elements ordered from most frequently accessed to least."""
#------------------------------ nested _Item class ------------------------------
class _Item:
__slots__ = '_value', '_count' # streamline memory usage
def __init__(self, e):
self._value = e # the user's element
self._count = 0 # access count initially zero
#------------------------------- nonpublic utilities -------------------------------
def _find_position(self, e):
"""Search for element e and return its Position (or None if not found)."""
walk = self._data.first()
while walk is not None and walk.element()._value != e:
walk = self._data.after(walk)
return walk
def _move_up(self, p):
"""Move item at Position p earlier in the list based on access count."""
if p != self._data.first(): # consider moving...
cnt = p.element()._count
walk = self._data.before(p)
if cnt > walk.element()._count: # must shift forward
while (walk != self._data.first() and
cnt > self._data.before(walk).element()._count):
walk = self._data.before(walk)
self._data.add_before(walk, self._data.delete(p)) # delete/reinsert
#------------------------------- public methods -------------------------------
def __init__(self):
"""Create an empty list of favorites."""
self._data = PositionalList() # will be list of _Item instances
def __len__(self):
"""Return number of entries on favorites list."""
return len(self._data)
def is_empty(self):
"""Return True if list is empty."""
return len(self._data) == 0
def access(self, e):
"""Access element e, thereby increasing its access count."""
p = self._find_position(e) # try to locate existing element
if p is None:
p = self._data.add_last(self._Item(e)) # if new, place at end
p.element()._count += 1 # always increment count
self._move_up(p) # consider moving forward
def remove(self, e):
"""Remove element e from the list of favorites."""
p = self._find_position(e) # try to locate existing element
if p is not None:
self._data.delete(p) # delete, if found
def top(self, k):
"""Generate sequence of top k elements in terms of access count."""
if not 1 <= k <= len(self):
raise ValueError('Illegal value for k')
walk = self._data.first()
for j in range(k):
item = walk.element() # element of list is _Item
yield item._value # report user's element
walk = self._data.after(walk)
def __repr__(self):
"""Create string representation of the favorites list."""
return ', '.join('({0}:{1})'.format(i._value, i._count) for i in self._data)
if __name__ == '__main__':
fav = FavoritesList()
for c in 'hello. this is a test of mtf': # well, not the mtf part...
fav.access(c)
k = min(5, len(fav))
print('Top {0}) {1:25} {2}'.format(k, [x for x in fav.top(k)], fav))
7.6.2 启发式动态调整列表¶
先前收藏夹列表的实现所执行的 access(e) 方法与收藏夹列表中 e 的索引存在时间上的比例关系。也就是说,如果 e 是收藏夹列表中第 k 个最受欢迎的元素,那么访问元素 e 的时 间复杂度就是 O(k) 。在许多实际的访问序列中(如,用户访问网页),如果一个元素被访问, 那么它很有可能在不久的将来再次被访问。这种情况被称为具有访问的局部性。
启发式算法(或称为经验法则),尝试利用访问的局部性,就是在访问序列中采用 Move-to-Front 启发式。为了应用启发式算法,我们每访问一个元素,都会把该元素移动到列表的最前面。当然,我们这么做是希望这个元素在近期可以被再次访间。例如, 考虑一个场景.在这个场景中,我们有 n 个元素和以下 \(n^2\) 次访问:
-
元素 1 被访问 n 次。
-
元素 2 被访问 n 次。
-
……
-
元素 n 被访问 n 次。
如果将元素按它们被访问的次数进行存储, 当元素第一次被访问时将元素插入队列,则:
- 对元素 1 的每次访问所花费的时间为 O(1) 。
- 对元素 2 的每次访问所花费的时间为 O(2) 。
- ……
- 对元素 n 的每次访问所花费的时间为 O(n)
因此,执行一系列访问的总时间就可以按比例地计算为:
\(n + 2n + 3n + ... + n\cdot n = n(1 + 2 + 3 + ... + n)=n\cdot n(n + 1)/2\),即为 \(O(n^3)\)
但是, 如果使用 Move-to-Front 启发式算法,在每个元素第一次被访问时将它插入,则
- 元素 1 的每个后续访问所花费的时间为 O(1) 。
- 元素 2 的每个后续访问所花费的时间为 O(1) 。
- ……
- 元素 n 的每个后续访问所花费的时间为 O(1) 。
所以,在这个案例中,执行所有访问的运行时间为 \(O(n^3)\) 。因此,这个场景的 Move-toFront 实现具有更短的访问时间。然而. Move-to-Front 只是一个启发式算法,因为这种使用 Move-to-Front 方法访问序列比简单地保存根据访问数量排序的收藏夹列表更慢。
Move-to-Front 启发式的权衡¶
当要求寻找收藏夹列表中前 k 个访问最多的元素时,如果不再保存列表中通过访问次数排序的元素, 就需要搜索所有元素。实现 top(k) 方法的步骤如下:
- 将所有收藏夹列表中的元素复制到另一个列表,并将该列表命名为 temp 。
2) 扫描 temp 列表 k 次,每次扫描时,找出访问量最大的元素记录, 从 temp 中移除这条记录,并且在结果中给出报告。
实现 top 方法的时间复杂度是 O(kn) ,因此,当 k 是一个常数时, top 方法的运行时间复杂度为 O(n) 。例如,想得到 “ top ten " 列表,就是这种情况。但是,如果 k 和 n 是成比例的,那么 top 运行时间复制度为 \(O(n^2)\) ,例如,我们需要一个 “ top 25% " 列表时。
在第 9 章中,我们将介绍一种以 \(O(n + k\log n)\) 的时间复杂度实现 top 方法的数据结构 (见练习 P-9.54) , 并且可以使用更多先进的技术在 O(n + klogn) 时间复杂度内来实现 top 方法。
如果在报告前 k 个元素之前,使用一个标准的排序算法来对临时列表重新排序(见 12 章),很容易地实现 O(n logn) 的时间复杂度。这种方法在 k 是 \(\Omega(\log n)\) 的情况下优于原始方法(回想 3.3.1 节中介绍的大 Ω 概念,它给出了一个更接近运行时间下限的排序算法) 。还 有更多专门的排序算法(见 12.4.2 节) ,这些算法可以借助访问次数是整数实现对任何一个 k 值, top 方法的时间复杂度为 O(n) 。
用 python 实现 More-to-Front 启发式¶
在代码段 7-20 中,我们给出了一个采用 Move-to-Front 启发式实现的收藏夹列表。其中的新 FavoritesListMTF 类继承了原始 FavoritesList 基类的绝大部分功能。
在最初的设计中,原始类的 access 方法依赖于一个非公共的实体_move_up , 在列表中, 一个元素的访问次数增加之后,使该元素向潜在的向前的位置调整。因此, 我们通过简单地重载_move_up 方法的方式实现 More-to-Front 启发式,从而使每个被访问的元素都被直接移动到列表的前端(如果之前不在前端的话) 。这个动作很容易通过位置列表的方法来实现。
FavoritesListMTF 类中更复杂的部分是 top 方法的新定义。我们借助上文所概述的第一种方法,将条目的副本插入临时列表中,然后重复地查找、报告,移除在剩余元素中访问量最大的元素。
from .favorites_list import FavoritesList
from .positional_list import PositionalList
class FavoritesListMTF(FavoritesList):
"""List of elements ordered with move-to-front heuristic."""
# we override _move_up to provide move-to-front semantics
def _move_up(self, p):
"""Move accessed item at Position p to front of list."""
if p != self._data.first():
self._data.add_first(self._data.delete(p)) # delete/reinsert
# we override top because list is no longer sorted
def top(self, k):
"""Generate sequence of top k elements in terms of access count."""
if not 1 <= k <= len(self):
raise ValueError('Illegal value for k')
# we begin by making a copython of the original list
temp = PositionalList()
for item in self._data: # positional lists support iteration
temp.add_last(item)
# we repeatedly find, report, and remove element with largest count
for j in range(k):
# find and report next highest from temp
highPos = temp.first()
walk = temp.after(highPos)
while walk is not None:
if walk.element()._count > highPos.element()._count:
highPos = walk
walk = temp.after(walk)
# we have found the element with highest count
yield highPos.element()._value # report element to user
temp.delete(highPos) # remove from temp list
if __name__ == '__main__':
fav = FavoritesListMTF()
for c in 'hello. this is a test of mtf':
fav.access(c)
k = min(5, len(fav))
print('Top {0}) {1:25} {2}'.format(k, [x for x in fav.top(k)], fav))
7.7 基于链表的序列与基于数组的序列¶
我们以思考之前介绍过的基于数组和基于链接的数据结构的 pros 和 cons 之间的联系来作为本章的结尾。当选择一个合适的数据结构的实现方法时,这些方法中呈现了一个共同的设计结果, 即两面性。就像每个人都有优点和缺点一样, 没办法找到一个万全的解决方案。
基于数组的序列的优点¶
- 数组提供时间复杂度为 O(1) 的基于整数索引的访问一个元素的方法。对于任何 k 值 以时间复杂度 O(1) 访问第 k 个元素的能力是一个数组的优点(见 5.2 节) 。相应地, 在一个链表中定位第 k 个元素要从起始位置遍历列表,其时间复杂度为 O(k) 。如果是反向遍历双向链表,则时间复杂度为 O(n - k)
- 通常,具有等效边界的操作使用基于数组的结构运行一个常数因子比基于链表的结构运行更有效率。例如,考虑一个针对队列的典型的 enqueue 操作。忽略调整数组大小的问题, ArrayQueue 类上的这个操作(见代码段 6-7) 包括一个新索引的计算算法、 一个整数的增量,并在数组中为元素存储一个引用。相反, LinkedQueue 的程序(见代码段 7-8) 要求节点的实例化、节点的合适链接和整数的增量。当这个操作用另一个模型在 O(1) 内完成时,链表版本中 CPU 操作的实际数量会更多,特别是考虑到新节点的实例化
- 相较于链式结构,基于数组的表示使用存储的比例更少。这个优点似乎是有悖于直觉的,特别是考虑到一个动态数组的长度可能超过它存储的元素的数量。基于数组的列表和链接列表都是可引用的结构,所以主存储器用于存储两种结构的元素的实际对象是相同的。而两者的不同点在于这两种结构使用的备用内存的数量。对于基于数组的 n 个元素的容器, 一种典型的最坏情况是调整动态数组来为 2n 个对象引用对应的分配内存。而对于链表,内存不仅要存储每个所包含的对象的引用,还要明确地存储链接这各个节点的引用。一个长度为 n 的单向链表至少需要 2n 个引用(每个节点的元素引用和指向下一个节点引用) 。
基于链表的序列的优点¶
- 基于链表的结构为它们的操作提供最坏情况的时间界限。这与动态数组的扩张和收缩相关联的摊销边界相对应(见 5.3 节) 。
当许多单个操作是一个大型计算的一部分时,我们仅关心计算的总时间,摊销边界和最坏情况的边界一样精确,因为它可以确保花费所有单个操作的时间总和。然而,如果数据结构操作用于一个实时系统,旨在提供更迅速的反应(如,操作系统、Web 服务器、空中交通控制系统),则单(摊销)操作导致的长时间延迟可能有不利影响。
- 基于链表的结构支持在任意位置进行时间复杂度为 O(1) 的插入和删除操作。 能够用 PositionalList 类实现常数时间复杂度的插入和删除操作,并通过使用 Position 有效地描述操作的位置, 这可能是链表最显着的优势。
这与基于数组的序列形成了鲜明的对比。 忽略调整数组大小的问题,任何从基于数组列表的末尾插入或删除一个元素的操作都可以在常数时间内完成。 然而,更普遍的插入和删除代价是很大的。 例如,用 python 的基于数组列表类,调用索引为 k 的插入和删除使用的时间复杂度为 O(n - k + 1) ,因为要循环替换所有后续元素 (见 5.4 节) 。
作为应用程序实例,考虑维护一个文件作为字符序列的文本编辑器。虽然用户经常在文件的末尾追加字符,还可能用光标在文件的任意位置插入和删除一个或多个字符。如果字符序列存储在一个基于数组的序列中(如, 一个 python 列表) ,每个编辑操作可能需要线性地调换许多字符的位置,导致每个编辑操作的 O(n) 性能。若用链表表示,任意一个编辑操作(在光标处的插入和删除)可以以最坏情况的时间复杂度 O(1) 执行,假设所给定的位置是表示光标的位置