第 8 章 树 ★
8.1 树的基本概念¶
生产力专家说,突破来源于“非线性”地思考问题。在本章中,我们来讨论一种最重要的非线性数据结构一树(tree) 。在数据的组织中,树结构的确是一个突破,因为我们用它实现的一系列算法比使用线性数据结构(诸如基于数组的列表或者链表)要快得多。树也为数据提供了一个更加真实、自然的组织形式,并由此在文件系统、图形用户界面、数据库、 网站和其他计算机系统中得以广泛使用。
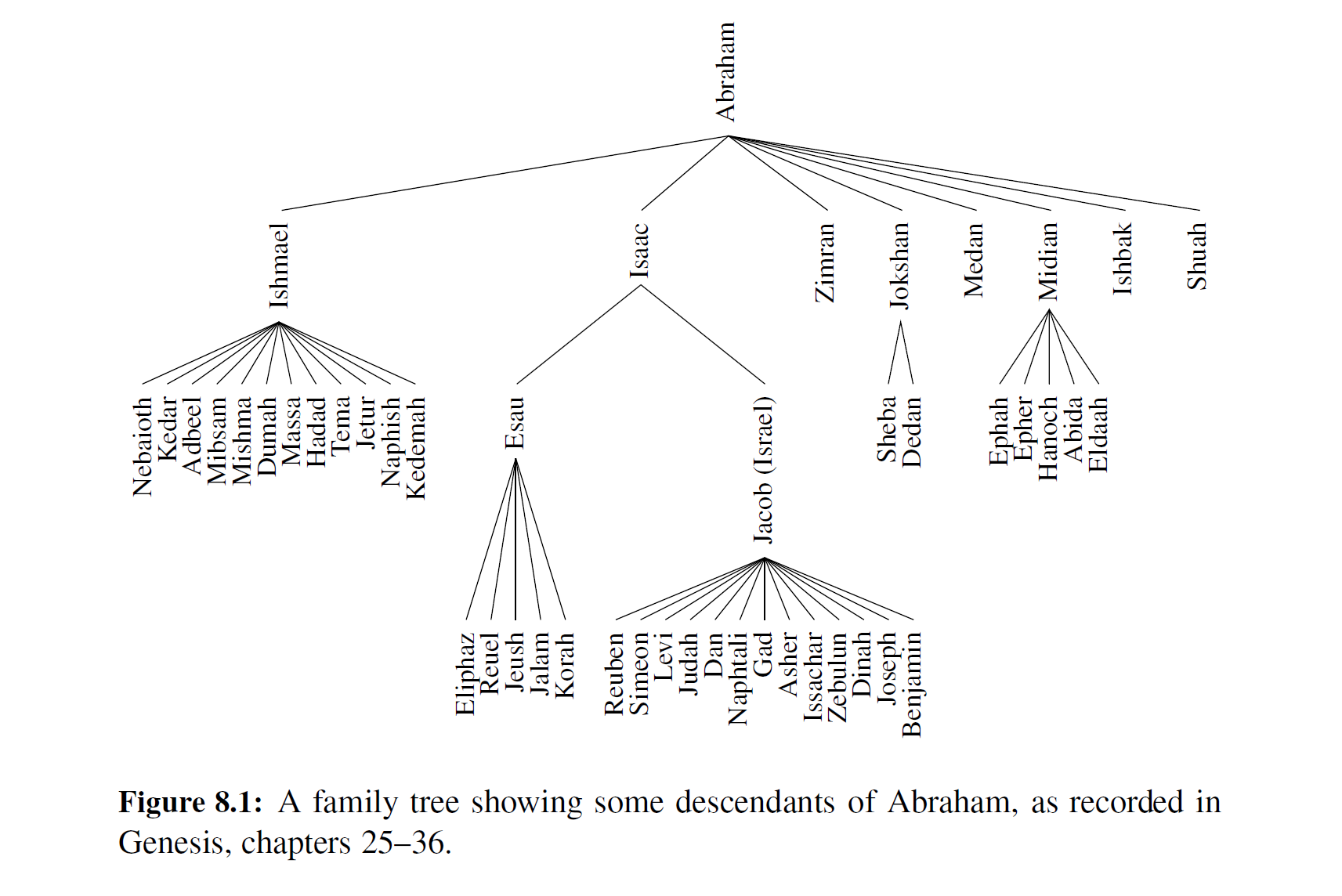
生产力专家口中的“非线性”思维并不总是那么清晰明了,但是说树形结构是“非线性” 时,我们指的是一种组织关系,这种组织关系要比一个序列中两个元素之间简单的 “ 前 ” 和 ” 后 “关系更加丰富和复杂。这种关系在树中是分层的(hierarchical) ,因为一些元素是处于 “上面的",而另一些是处于 ”下面的" 。事实上,树形数据结构的主要术语来源于家谱,因为术语“双亲”“孩子”“祖先”和“子孙”在描述这些关系时最为常见。图 8-1 所示即为一 个家谱图示例。
8.1.1 树的定义和属性¶
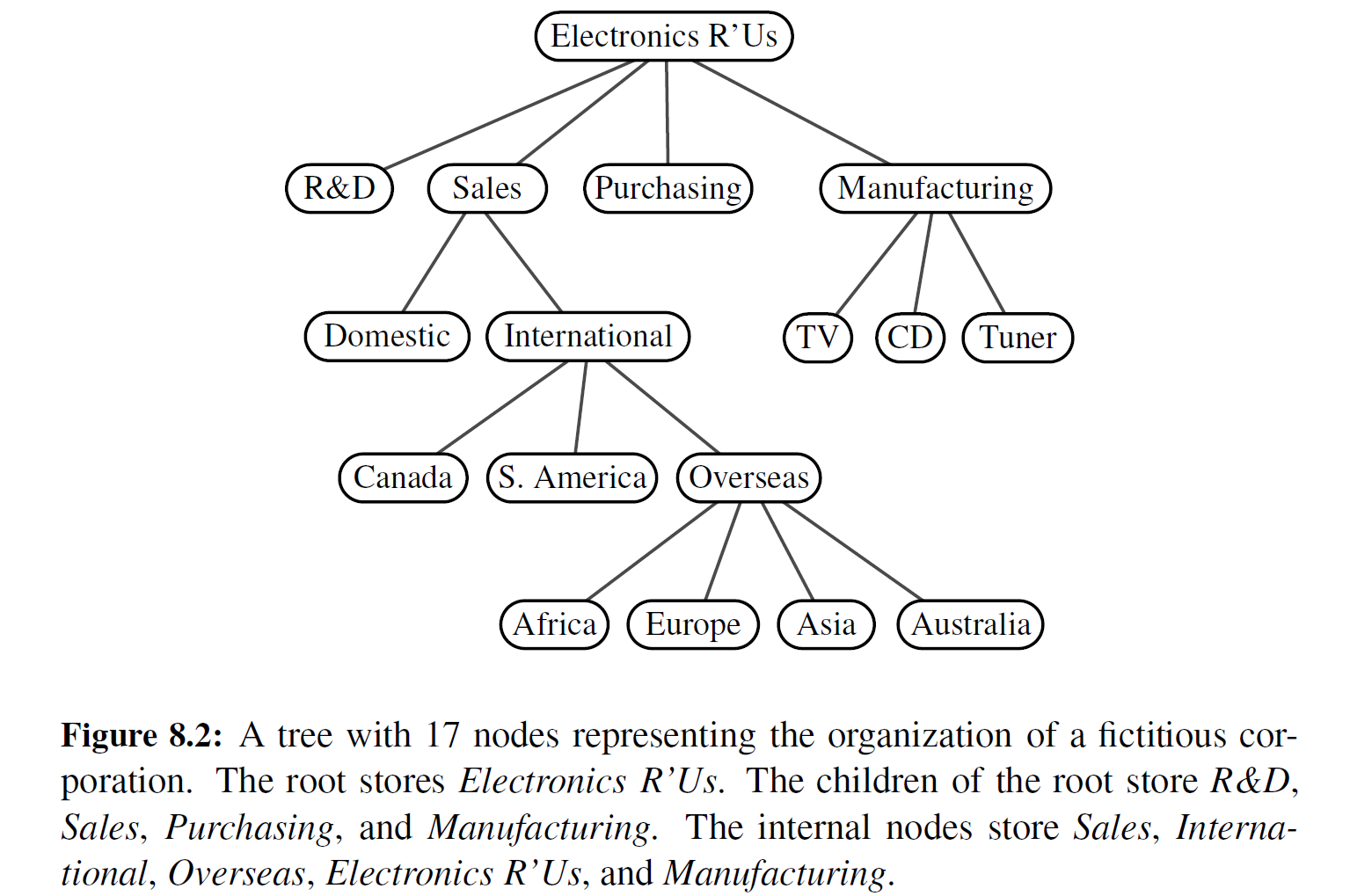
树是一种将元素分层次存储的抽象数据类型。除了最顶部的元素,每个元素在树中都有一个双亲节点和零个或者多个孩子节点。通常,我们通过将元素放置在一个椭圆形或者圆形中并且通过直线将双亲节点与孩子节点相连来图示化一棵树,如图 8-2 所示。我们通常称最顶部元素为树根(root) ,在图示中它被作为最顶部的元素,因为其他元素都被连接在它的下面(这与一棵真实世界中的树恰恰相反) 。
正式的树定义¶
通常我们将树 T 定义为存储一系列元素的有限节点集合,这些节点具有 parent-children 关系并且满足如下属性:
- 如果树 T 不为空,则它一定具有一个称为根节点的特殊节点,并且该节点没有父节点
- 每个非根节点 v 都具有唯一的父节点 w, 每个具有父节点 w 的节点都是节点 w 的一 个孩子。
注意,根据上述定义, 一棵树可能为空,这意味着它不含有任何节点。这个约定也允许我们递归地定义一棵树,以使这棵树 T 要么为空,要么包含一个节点 r (其称为树 T 的根节点),其他一系列子树的根节点是 r 的子节点。
其他节点关系¶
同一个父节点的孩子节点之间是兄弟关系。一个没有孩子的节点 v 称为外部节点。一个有一个或多个孩子的节点 v 称为内部节点。外部节点也称为叶子节点。
例题 8-1 :在 4.1.1 节中,我们讨论了计算机文件系统中文件与目录之间的分层关系, 尽管那个时候没有强调文件系统是树关系。我们重温一下先前的例子,如图 8 -3 所示。我们可以看到树的内部节点对应着文件的目录,而叶子节点对应着文件。在 UNIX 和 Linux 操作系统中,树的根节点称为 “根目录”,用符号 “/" 表示
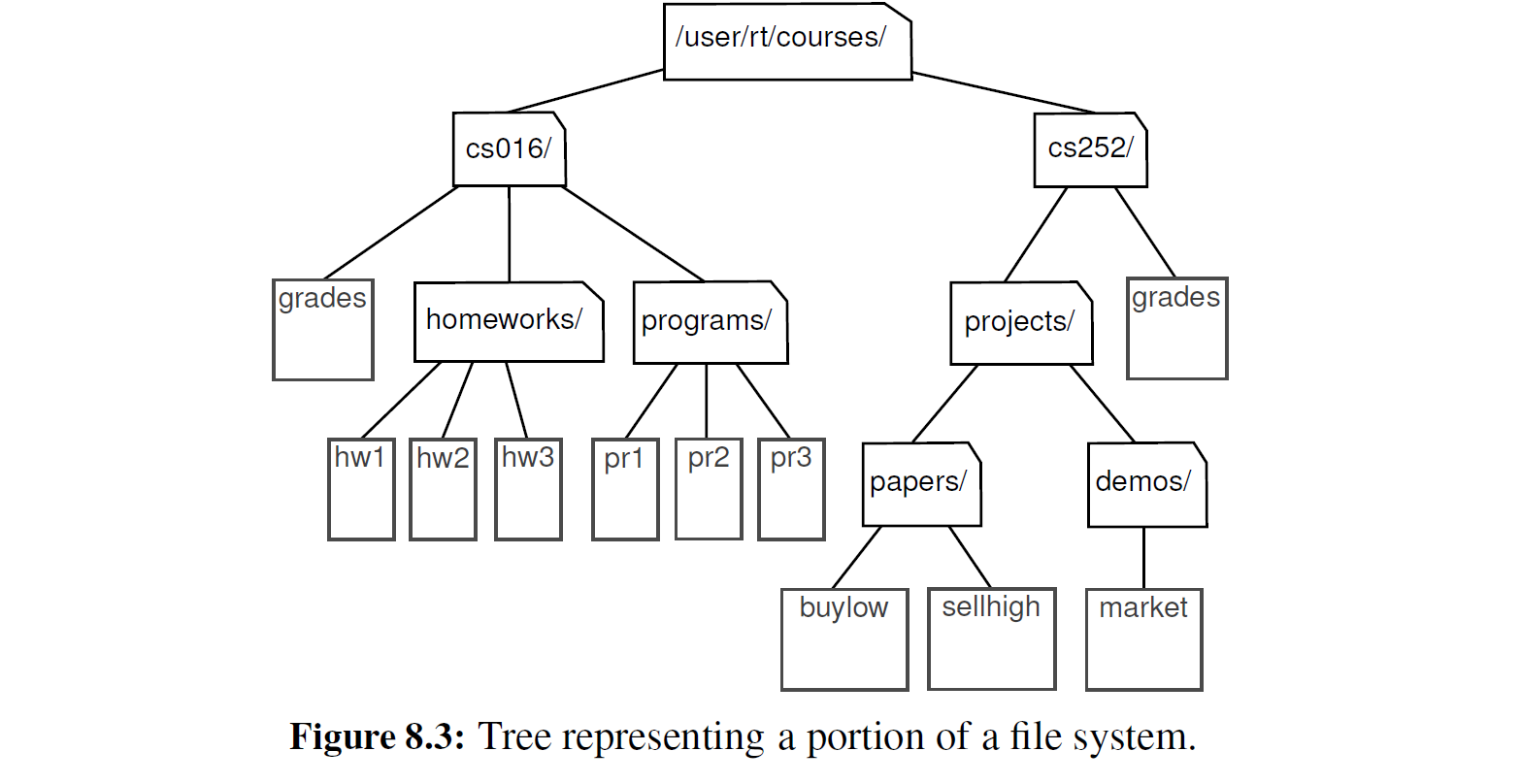
如果 u = v, 那么节点 u 是节点 v 的祖先或者是节点 v 父节点的祖先。反过来说,如果节点 u 是节点 v 的一个祖先,那么节点 v 就是节点 u 的一个子孙。例如,在图 8 -3 中, cs252/ 是 papers/ 的一个祖先而 pr3 是 cs016/ 的一个子孙。以节点 v 为根节点的子树包含树 T 中节 点 v 的所有子孙(包括节点 v 本身) 。在图 8-3 中,以 cs016/为根节点的子树包含的节点为 cs016/ 、grades 、homeworks/ 、programs/ 、hwl 、hw2 、hw3 、prl 、pr2 和 pr3
树的边和路径¶
树 T 的一条边指的是一对节点 (u, v), u 是 v 的父节点或 v 是 u 的父节点。树 T 当中的路径指的是一系列的节点,这些节点中任意两个连续的节点之间都是一条边。例如,图 8-3 包含了路径( cs252/ , projects/, demos/, market ) 。
例题 8-2: 在一个 python 程序中,当使用单继承时,类与类之间的继承关系形成了一棵树。例如,2.4 节给出了 python 异常类结构层次的总结,正如图 8-4 所示的一样(见图 2-5 ) 。这个 BaseException 类是该层次结构的根,而所有用户自定义的异常类按照惯例都应该声明为更加具体的异常类的后代。(例如,笫 6 章代码段 6- 1 中的 Empty 类。)
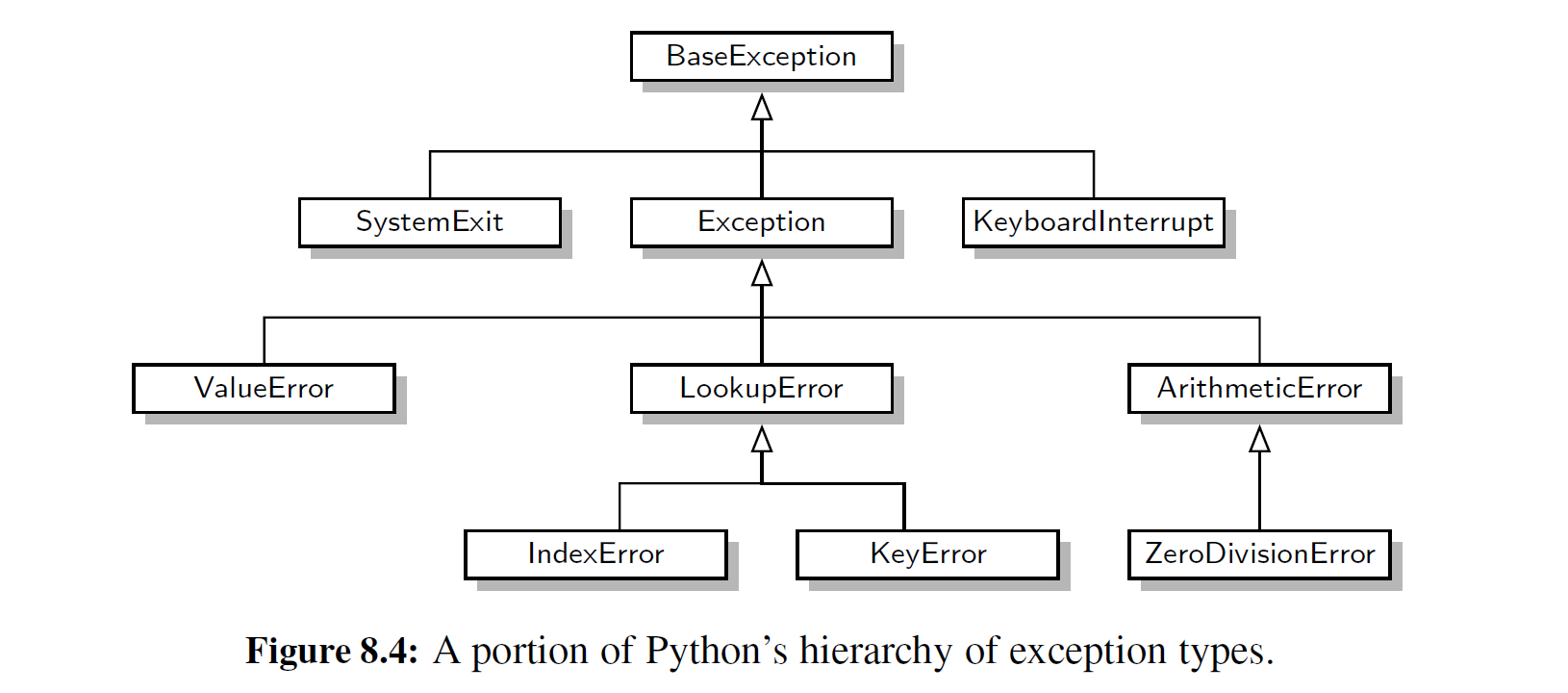
在 python 中,所有类被组织成单一的层次结构,因为存在一个名为 object 的内置类作为最终的基类。在 python 中,它是所有其他类型的直接或者间接的基类(即使在定义的时 候并没有这样声明) 。因此,图 8-4 所示的部分只是 python 类层次结构的一部分。
作为对本章剩余部分的一个预览,图 8-5 所示即为类的层次结构,这些类用于表示各种形式的树。
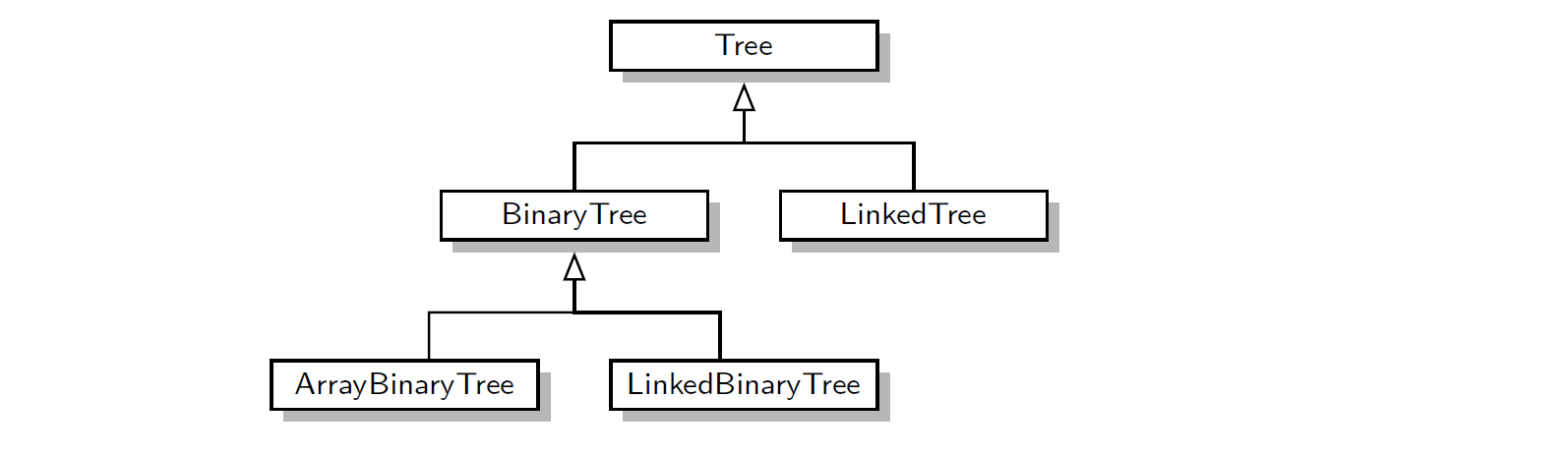
图 8-5 一个模拟各种树数据结构和各种抽象结构的层次结构。在本章的剩余部分,我们详细阐述了树的实现,二叉树、链式二叉树类,以及如何设计树的链式结构和基于数组的二叉树的高标准示意图
有序树¶
如果树中每个节点的孩子节点都有特定的顺序,则称该树为有序树,我们将一个节点的孩子节点依次编号为第一个、第二个、第三个等。通常我们按照从左到右的顺序对兄弟节点进行排序。
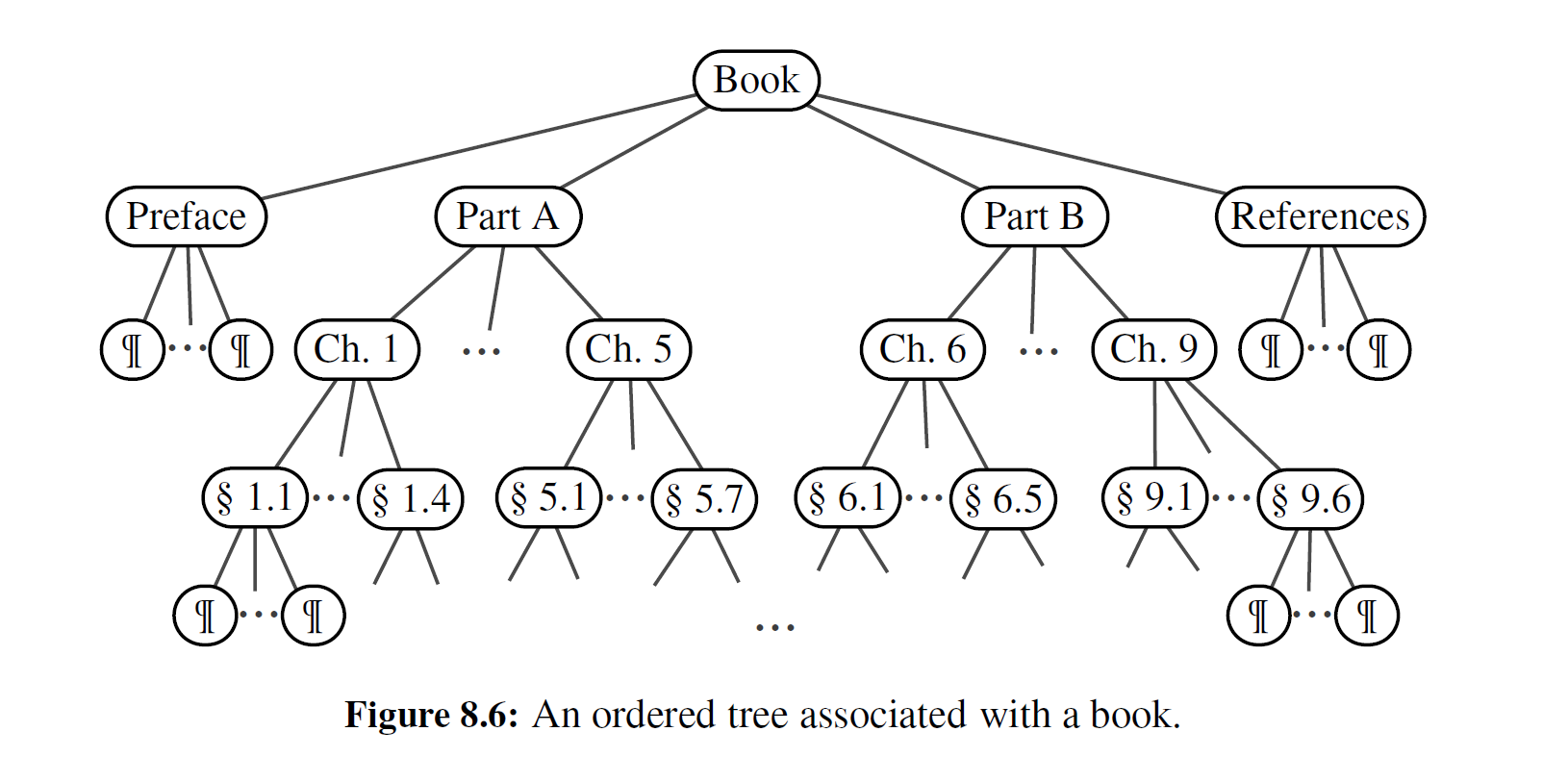
例题 8-3: 考虑结构化文档的内容,诸如一本书按树的样式分层组织,它的内部节点由章节构成,它的叶子节点由段落、表格、图片等构成(见图 8-6) ,树的根节点是书本身。事实上,我们可以进一步考虑对此进行扩展,如段落又是由句子组成的,而句子又是由单词构成的,单词又是由一个个字母组成的。这就是一棵有序树的典型例子。因为它们的每个孩子节点都具有很好的顺序
让我们回顾一下已经描述的树的例子,然后进一步深入思考孩子的顺序是否有意义。正如图 8-1 描述的家庭关系树,它总是根据成员的出生时间被模拟成一棵有序树。
相比之下,一个公司的组织结构图(见图 8-2) 却通常被认为是一棵无序树。同样,当使用一棵树来描述继承关系的分层结构时,正如图 8-4 所述,对一个父类的子类而言顺序并没有特别的意义。最后,我们考虑用树来描述计算机的文件系统,如图 8 -3 所示,尽管操作系统经常按照特定的顺序显示目录(例如,按字母或者时间顺序),但是这样的顺序对于文件系统的显示而言通常不是固定的。
8.1.2 树的抽象数据类型¶
正如我们在 7.4 节做的位置列表,我们用位置作为节点的抽象结构来定义树的抽象数据结构。一个元素存储在一个位置,并且位置信息满足树中的父节点与孩子节点的关系。一棵树的位置对象支持如下方法:
p.element():返回存储在位置 p 中的元素
树的抽象数据类型支持如下访问方法。允许使用者访问一棵树的不同位置:
T.root():返回树 T 的根节点的位置。如果树为空,则返回 None 。T.is_root(p): 如果位置 p 是树 T 的根,则返回 True 。T.parent(p): 返回位置为 p 的父节点的位置。如果 p 的位置为树的根节点,则返回 None 。T.num_children(p):返回位置为 p 的孩子节点的编号。T.children(p):产生位置为 p 的孩子节点的一个迭代。T.is_leaf(p):如果位置节点 p 没有任何孩子,则返回 True 。len(T):返回树 T 所包含的元素的数量。T.is_empty():如果树 T 不包含任何位置,则返回 True 。T.positions():迭代地生成树 T 的所有位置。iter(T):迭代地生成存储在树 T 中的所有元素
以上所有方法都接受一个位置作为参数,但是如果树 T 中的这个位置是无效的,则调用 它就会触发一个 ValueError 。
如果一棵树 T 是有序树,那么执行方法 T.children(p) 就会返回孩子节点 p 本身的顺序。如果 p 是一个叶子节点,那么执行方法 T.children(p) 就会导致一个空的迭代。与此类似,如果树 T 为空`那么执行方法 T.positions()和 iter(T) 也会导致一个空迭代。我们将在 8.4 节通过一棵树的所有位置来讨论迭代生成方法。
我们暂时还没有定义任何生成或者修改树的方法,而更乐于结合一些树接口的特定实现和一些树的特定应用来描述不同树的更新方法
python 中树的抽象基类¶
2.1.2 节讨论的抽象的面向对象的设计原则中,我们注意到 python 中一个抽象数据类型的公共接口经常是通过 duck typing 管理的。例如,我们在 6.2 节定义了一个队列 ADT 的公共接口概念(例如, 6.2.2 节的基于数组的队列, 7.1.2 节的链表, 7.2.2 节的循环链表) 。但我们在 python 中从来没有给出队列 ADT 的任何正式的定义;所有具体实现方法都是独立的类,这些独立的类遵循相同的公共接口。一种更正式的用于指定具有相同抽象但不同的实现方法之间的关系的机制,是通过类的定义,这个类是抽象的基类,它将通过继承产生一个或更多的具体类(见 2.4.3 节) 。
在代码段 8-1 中,我们选择定义一个 Tree 类充当一个与树的抽象数据结构相关的抽象基类。之所以这样做,是因为我们可以提供相当多的可用代码,即使是在这个抽象级别,在随后树的具体方法实现中也允许更多代码的重用。树的类提供了嵌套类(这些类也是抽象的) 的定义和树 ADT 中许多访问方法的申明。
然而,我们定义的 Tree 类并没有定义存储树的任何内部表示,并且在代码段中给出的 5 个方法(root 、parent 、num_ children.children 和__len__)仍然是抽象的。每个方法都会触发一个 NotlmplementedError() ( 一个更加正式的定义抽象方法和基类的方法是使用 2.4.3 节 描述的 python 的 abc 模块) 。比如孩子节点,为了给每个行为提供一个实现,子类基于它们自选的内部表示来重写抽象方法。
尽管 Tree 类是一个抽象的基类,但它包括几个具体的实现方法,这些方法依赖类的抽象方法的调用。在先前章节树的抽象数据结构的定义中,我们声明了 10 种访问方法。其中 的 5 个是抽象的,在代码段 8-1 中给出。剩下的 5 个是基于前面 5 个实现的。代码段 8-2 列出了方法 is_root 、is_leaf 和 is_empty 的具体实现。在 8.4 节中,我们将会探索树的遍历方法, 其能够为位置的确定和__iter__方法提供一个具体的实现。这种设计的好处是,在树的抽象基类中定义的所有具体方法都能被它的子类所继承。这有助于代码重用,因为对子类而 言没有重新实现这些方法的必要。
可以注意到,由于树类是抽象的,因此我们没有理由为其创建一个实例,或者即使创建了一个实例,这个实例也是没有用的。这个类的存在只是作为其他子类用于继承的基础,用户将会创建具体子类的实例。
from ..ch07.linked_queue import LinkedQueue
import collections
class Tree:
"""Abstract base class representing a tree structure."""
#------------------------------- nested Position class -------------------------------
class Position:
"""An abstraction representing the location of a single element within a tree.
Note that two position instaces may represent the same inherent location in a tree.
Therefore, users should always rely on syntax 'p == q' rather than 'p is q' when testing
equivalence of positions.
"""
def element(self):
"""Return the element stored at this Position."""
raise NotImplementedError('must be implemented by subclass')
def __eq__(self, other):
"""Return True if other Position represents the same location."""
raise NotImplementedError('must be implemented by subclass')
def __ne__(self, other):
"""Return True if other does not represent the same location."""
return not (self == other) # opposite of __eq__
# ---------- abstract methods that concrete subclass must support ----------
def root(self):
"""Return Position representing the tree's root (or None if empty)."""
raise NotImplementedError('must be implemented by subclass')
def parent(self, p):
"""Return Position representing p's parent (or None if p is root)."""
raise NotImplementedError('must be implemented by subclass')
def num_children(self, p):
"""Return the number of children that Position p has."""
raise NotImplementedError('must be implemented by subclass')
def children(self, p):
"""Generate an iteration of Positions representing p's children."""
raise NotImplementedError('must be implemented by subclass')
def __len__(self):
"""Return the total number of elements in the tree."""
raise NotImplementedError('must be implemented by subclass')
# ---------- concrete methods implemented in this class ----------
def is_root(self, p):
"""Return True if Position p represents the root of the tree."""
return self.root() == p
def is_leaf(self, p):
"""Return True if Position p does not have any children."""
return self.num_children(p) == 0
def is_empty(self):
"""Return True if the tree is empty."""
return len(self) == 0
return entire preorder iteration
8.1.3 计算深度和高度¶
假定 p 是树 T 中的一个节点,那么 p 的深度就是节点 p 的祖先的个数,不包括 p 本身
例如,在图 8-2 的树中,节点 International 的深度为 2 。需要注意的是,这种定义表明树的根节点的深度为 0 。p 的深度同样也可以按如下递归定义:
- 如果 p 是根节点,那么 p 的深度为 0
- 否则, p 的深度就是其父节点的深度加 1
基于这个定义,我们在代码段 8-3 中给出了计算树 T 中一个节点 p 的深度的简单递归算法。该算法递归地调用自身。
def depth(self, p):
"""Return the number of levels separating Position p from the root."""
if self.is_root(p):
return 0
else:
return 1 + self.depth(self.parent(p))
对于位置 p, 方法 T.depth(p) 的运行时间是 O(\(d_p+1\)) ,其中 \(d_p\) 指的是树 T 中 p 节点的深度,因为该算法对于 p 的每个祖先节点执行的时间是常数。因此算法 T.depth(p) 在最坏的情况下运行时间为 O(n) 。其中 n 是树中节点的总个数。因为如果所有节点组成一个分支,那 么其中存在一个节点的深度将为 n - 1 。尽管这个运行时间是输入大小的函数,但是对于运行时间参数 \(d_p\) 更加具有决定性。因为这个参数通常情况下远小于 n 。
树 T 中节点 p 的高度的定义如下:
- 如果 p 是一个叶子节点,那么它的高度为 0 。
- 否则, p 的高度是它孩子节点中的最大高度加 1 。
一棵非空树 T 的高度是树根节点的高度。例如,图 8-2 所示的树的高度为 4 。除此之外,高度还可以定义如下:
命题 8-4: 一棵非空树 T 的高度等于其所有叶子节点深度的最大值
我们在练习 R-8.3 中给出了这个命题的证明。我们在代码段 8-4 中给出了一个算法 height1 ,其作为 Tree 类的一个私有方法。该算法基于命题 8-4 和代码段 8-3 的计算深度的算法来计算一棵非空树的高度。
def _height1(self): # works, but O(n^2) worst-case time
"""Return the height of the tree."""
return max(self.depth(p) for p in self.positions() if self.is_leaf(p))
不幸的是,算法 height1 并不高效。我们目前还没有定义 position() 方法,可以看到该算法的执行时间是 O(n) ,其中 n 是树 T 中的节点个数。因为 height1 算法针对每个叶子节点都调用了算法 depth(p) ,其执行时间为 \(O(n+\sum_{p\in L}(d_p+ 1))\),其中 L 是树 T 叶子节点的集合。最坏情况下, \(\sum_{p\in L}(d_p+1)\) 与 \(n^2\) 成正比(详见练习 C-8.33) 。因此,算法 height1 在最坏情况下的执行时间为 O(\(n^2\))
在最坏情况下,不依赖先前的递归定义,我们可以更加高效地计算树的高度,使其执行时间为 O(n) 。为了这样做,我们将基于一棵树中的某个位置参数化一个函数,并计算以这个节点作为根节点的子树的高度。代码段 8-5 给出的算法 height2 就是通过这种方式来计算树的高度。
def _height2(self, p): # time is linear in size of subtree
"""Return the height of the subtree rooted at Position p."""
if self.is_leaf(p):
return 0
else:
return 1 + max(self._height2(c) for c in self.children(p))
理解算法 height2 为什么比算法 height1 更高效很重要。该算法是递归的并且是从上到下执行的。如果该算法最初在根节点调用,那么树 T 的每个节点最终将会被调用。这是因为树的根节点最终将在其每个孩子节点上递归调用,这反过来又将在每个节点的孩子节点中继续递归调用下去。
我们可以通过加上所有花在每个节点上的递归调用的时间来计算算法 height2 的运行时 间(复习 4.2 节递归调用的分析过程) 。在实现方法中,对于每个节点,有一个不变的常量以及计算每个孩子节点的最大负载。尽管我们还没有构造 children(p) 的实现方法,但可以假设生成时间是 O(\(c_p + 1\)) ,其中 \(c_p\) 是 p 节点孩子节点的个数。算法 height2 在每个节点上最多需要花 O(\(c_p+ 1\)) 的时间,所以整个时间为 \(O(\sum_p(c_p+ 1)) = O(n +\sum_pc_p)\) 。为了完成分析,我们使用如下定义。
命题 8-5: 假设 T 是一棵有 n 个节点的树,并假设 \(c_p\) 代表树 T 中位置 p 的孩子节点的个数,那么 T 中所有节点的位置之和为\(\sum_pc_p=n-1\)
证明: 树 T 中除了根节点外的每个位置,都是另一个节点的孩子节点,并且都会成为上面公式的一项。
由命题 8-5 可知,在根节点调用算法 height2 时,其执行时间为 O(n) ,其中 n 为树中节 点的个数。
重新访问 Tree 类的公共接口,计算子树的高度是有益的,但是用户可能希望能够计算整个树的高度而不需要显式地指定树的根节点。我们可以通过一个公有的 height 方法将非公有的方法_heigbt2 封装在实现方法中。在树 T 中调用 T. heigbt()方法时, height 方法提供了一个默认的解释。其实现的过程如代码段 8-6 所示。
def height(self, p=None):
"""Return the height of the subtree rooted at Position p.
If p is None, return the height of the entire tree.
"""
if p is None:
p = self.root()
return self._height2(p) # start _height2 recursion
8.2 二叉树¶
二叉树是具有以下属性的有序树:
- 每个节点最多有两个孩子节点。
- 每个孩子节点被命名为左孩子或右孩子。
- 对于每个节点的孩子节点,在顺序上,左孩子先于右孩子。若子树的根为内部节点 v 的左孩子或右孩子,则该子树相应地被称为节点 v 的左子树或右子树。若每个节点都有零个或两个节点,则这样的二叉树为完全二叉树。一些人也把这种树称为满二叉树。因此,在完全二叉树中,每个内部节点都恰好有两个孩子。若二叉树不完全,则称为不完全二叉树。
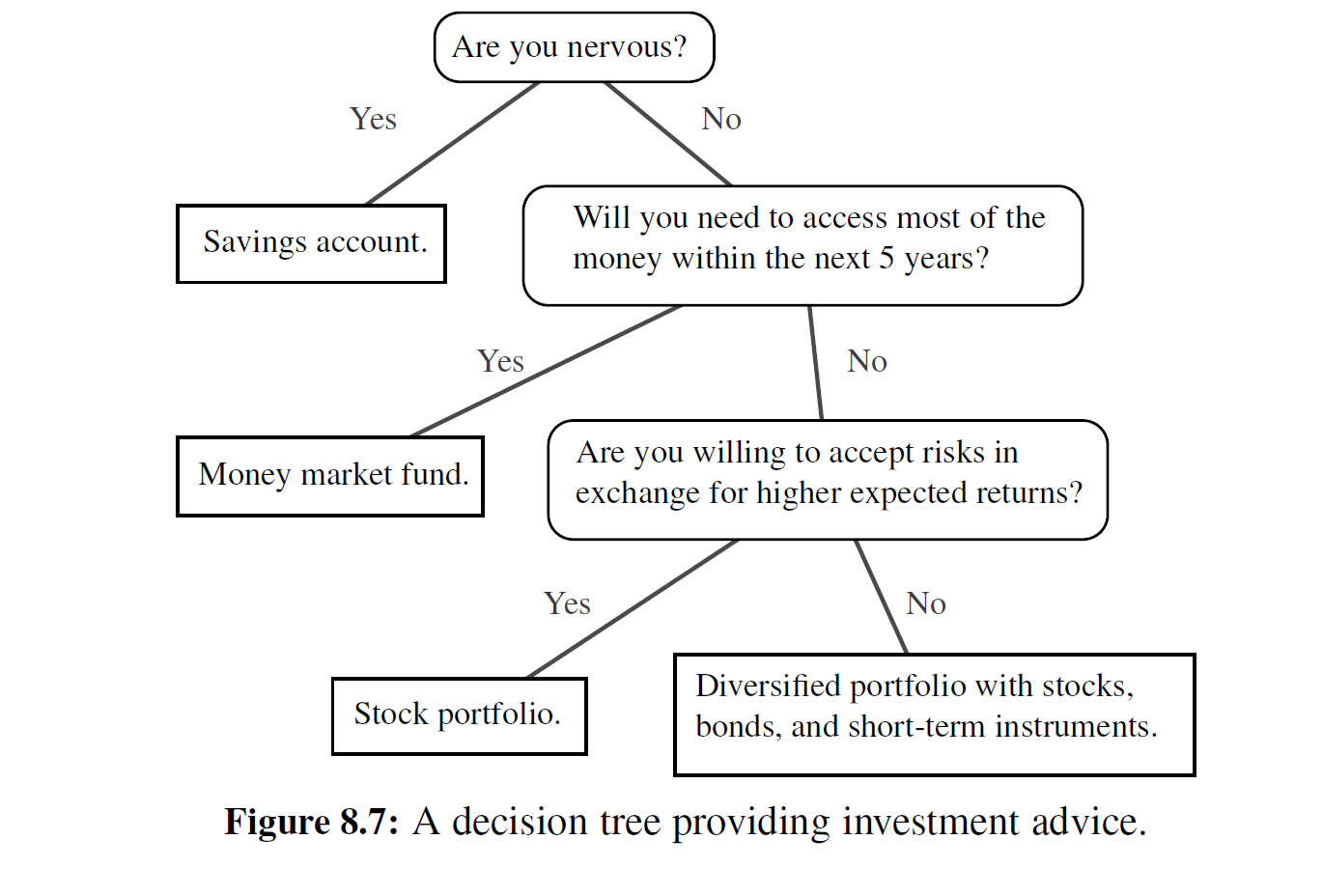
例题 8-6: 二叉树的一个重要的类适用于这样的情形:我们希望能(使用此类)表示许多种不同的输出结果,这些结果可以作为一系列 yes-or-no 问题的答案。
每个内部节点对应一个问题。从根节点开始,我们根据该问题的答案是 “Yes" 还是 “No" 来决定当前节点是左孩子还是右孩子。对于每次决定,相当于选择了从父节点到子节点的一条边,最终能形成一条从根节点到叶节点的路径。这样的二叉树被称为决策树,因为若与树 中叶节点 p 的祖先节点相关的问题都被回答,以得到 p 的结果,那么 p 即表示为一种需要做什么的决策。决策树是完全二叉树。图 8-7 给出了能给未来投资者提供建议的 一棵决策树。
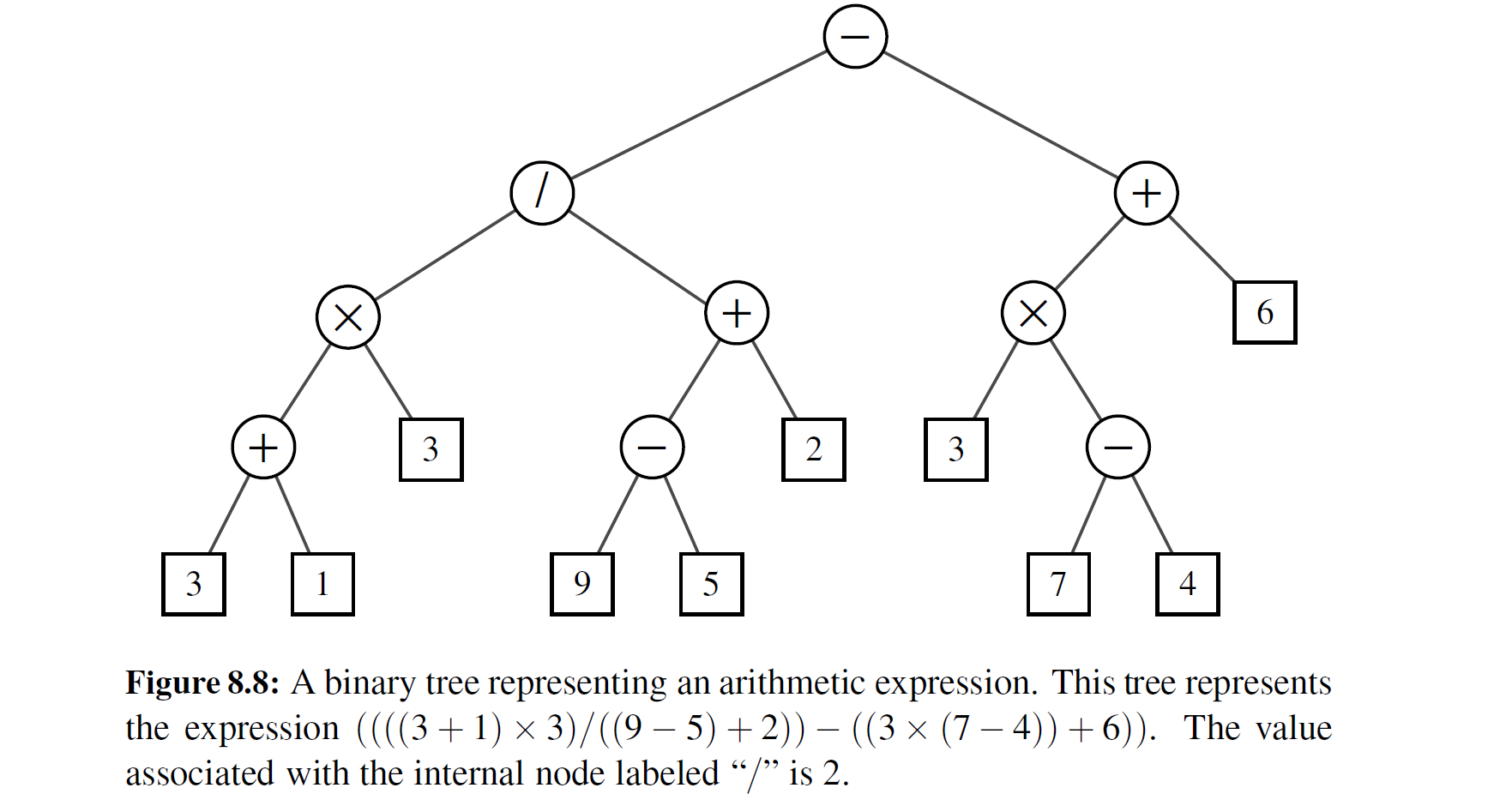
例题 8-7: 二叉树能用于表示算术表达式,叶子对应变量或常数,内部节点 对应+、-、× 和/操作(见图 8-8 ) 。树中的每个节点都对应一个值
- 若节点为叶节点,则其值为变量或常数。
- 若节点为内部节点,则其值为对其孩子节点值的操作所得。
算术表达式树是完全二叉树,因为 每个+ 、- 、× 、/ 都需要两个操作数。当然,如果允许一元操作符,例如负号 (-),表示为"-× "'也可以得到不完全二叉树。
递归二叉树的定义
我们也能够顺便使用递归方式定义二叉树,此时二叉树或者为空树,或者由以下条件组成:
- 二叉树 T 的根为节点 r, 其存储一个元素
- 二叉树(可能为空)称为 T 的左子树
- 二叉树(可能为空)称为 T 的右子树
8.2.1 二叉树的抽象数据类型¶
作为抽象数据类型,二叉树是树的一种特殊化,其支持 3 种额外的访问方法:
T.left(p):返回 p 左孩子的位置,若 p 没有左孩子, 则返回 NoneT.right(p):返回 p 右孩子的位置,若 p 没有右孩子,则返回 NoneT.sibling(p):返回 p 兄弟节点的位置,若 p 没有兄弟节点,则返回 None
类似于 8.1.2 节对树 ADT 的处理,此处不专门对二叉树定义更新方法。而是在描述二叉树具体的实现和应用时, 才去考虑一些可能的更新方法。
python 中的抽象基类 BinaryTree¶
在 8.1.2 节中,我们将 Tree 定义为抽象基类。类似地,我们在已存在的 Tree 类基础上, 依据继承性,对二叉树 ADT 定义一个新的 BinaryTree 类。然而, BinaryTree 类保持抽象性, 因为对于这样的一个结构,我们并没有提供完整的内部细节描述,也没有实现一些必要的行为。
在代码段 8-7 中,我们给出了 BinaryTree 类的 python 实现。根据继承性, 二叉树支持在一般的树中定义的所有功能(例如, parent 、is_leaf 和 root ) 。新类也继承嵌套的 Position 类,该类一开始就定义在 Tree 类的定义中。另外,新类声明了新的抽象方法 left 和 right , 这些方法应能在 BinaryTree 类的具体子类中实现。
新类也给出了两种方法的具体实现。新的 sibling 方法由 left 、right 和 parent 结合产生。具有代表性的是,我们把位置 p 的兄弟节点定义为 p 双亲节点的"另一个 “ 孩子节点。若 p 是根节点,因为没有双亲节点,所以也没有兄弟节点。另外, p 可能是其双亲节点唯一的孩 子,因而此时也无兄弟节点。
最后,代码段 8-7 给出了 children 方法的具体实现,该方法在 Tree 类中是抽象的。尽管我们仍未具体说明节点的孩子是如何存储的,但能通过抽象的 left 和 right 方法的隐含行为产生有序的孩子。
from .tree import Tree
class BinaryTree(Tree):
"""Abstract base class representing a binary tree structure."""
# --------------------- additional abstract methods ---------------------
def left(self, p):
"""Return a Position representing p's left child.
Return None if p does not have a left child.
"""
raise NotImplementedError('must be implemented by subclass')
def right(self, p):
"""Return a Position representing p's right child.
Return None if p does not have a right child.
"""
raise NotImplementedError('must be implemented by subclass')
# ---------- concrete methods implemented in this class ----------
def sibling(self, p):
"""Return a Position representing p's sibling (or None if no sibling)."""
parent = self.parent(p)
if parent is None: # p must be the root
return None # root has no sibling
else:
if p == self.left(parent):
return self.right(parent) # possibly None
else:
return self.left(parent) # possibly None
def children(self, p):
"""Generate an iteration of Positions representing p's children."""
if self.left(p) is not None:
yield self.left(p)
if self.right(p) is not None:
yield self.right(p)
8.2.2 二叉树的属性¶
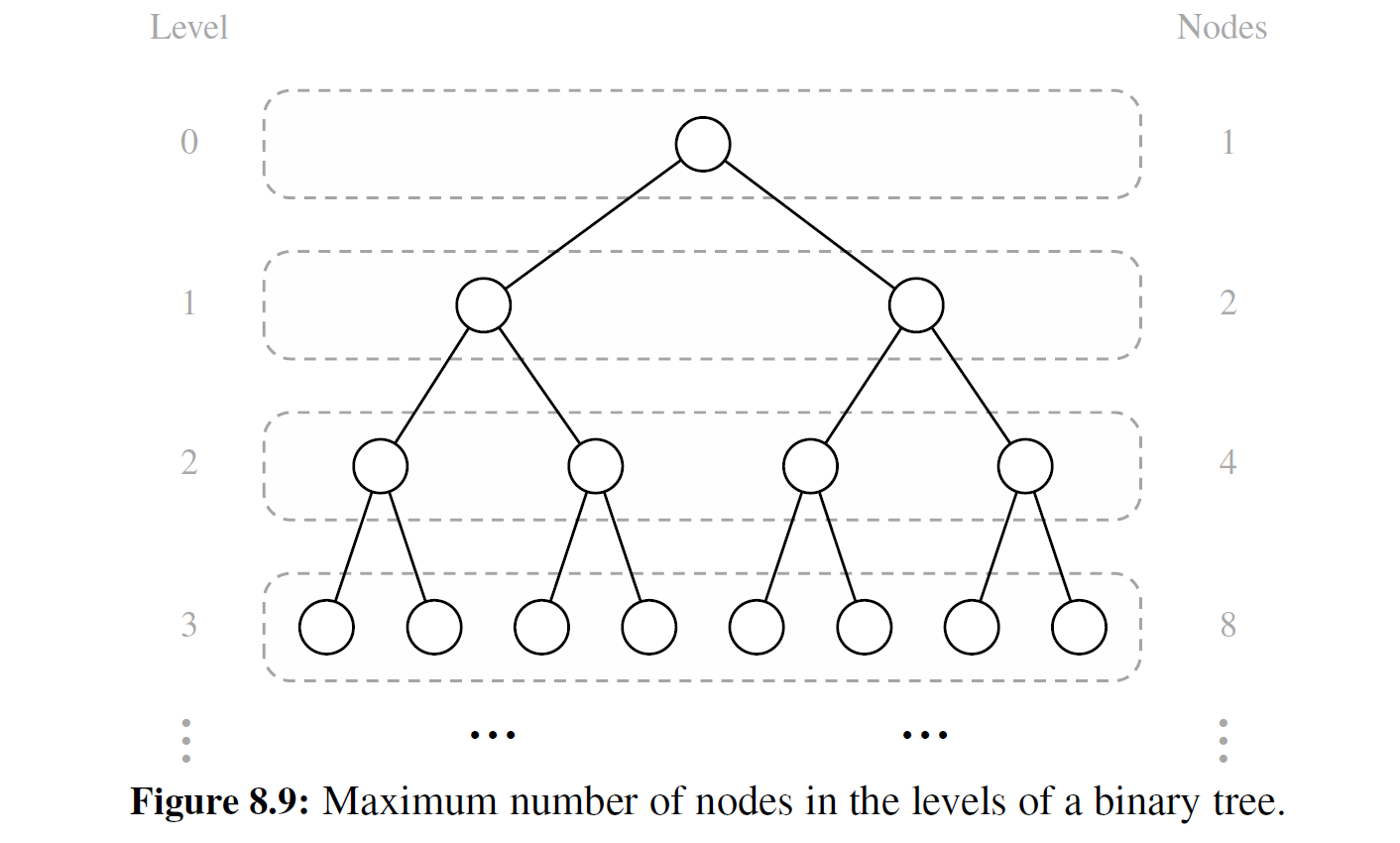
二叉树在处理其高度和节点数的关系时有几个有趣的性质。我们将位于树 T 同一深度 d 的所有节点都视为位于 T 的 d 层。在二叉树中, 0 层至多有一个节点(根节点), 1 层至多有两个节点(根节点的孩子), 2 层至多有 4 个节点,以此类推(见图 8-9 ) 。总之, d 层至多有 \(2^d\) 个节点
我们注意到, 当沿着二叉树往下遍历时,每层的最大节点数呈指数增长。通过这个简单的观察,我们可以, 得出二叉树 T 的高度与节点数之间的性质。这些性质的详细证明留作练习 R-8.8 。
命题 8-8: 设 T 为非空二又树, \(n,n_E,n_I\) 和 \(h\) 分别表示 T 的节点数、外部节点数、内部节点数和高度,则 T 具有如下性质:
- \(h+1\le n \le 2^{k+1}-1\)
- \(1\le n_E\le2^h\)
- \(h\le n_I\le2^h-1\)
- \(\log(n+1)-1\le h\le n-1\)
另外, 若 T 是完全二叉树,则 T 具有如下性质:
- \(2h+1\le n\le2^{h+1}-1\)
- \(h+1\le n_E\le2^h\)
- \(h\le n_I\le2^h-1\)
- \(\log(n + 1)-1 \le h \le (n-1)/2\)
完全二叉树中内部节点与外部节点的关系¶
除了前面二叉树的性质,下述关系存在于完全二叉树中内部节点数与外部节点数之间。
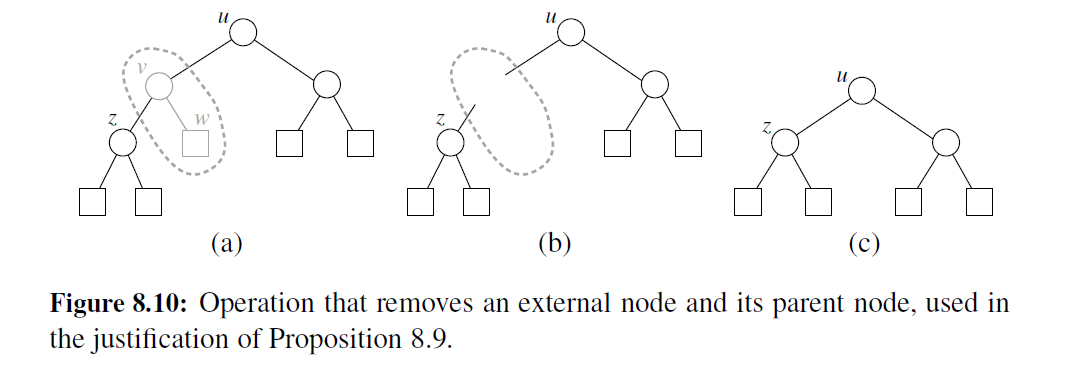
命题 8-9: 在非空完全二叉树 T 中,有 \(n_E\) 个外部节点和 \(n_I\) 个内部节点,则有 \(n_E=n_I+1\) 。
证明: 从 T 中取下节点,并把它们分别放入两个"桩",即内部节点桩和外部节点桩, 直到 T 为空。两个桩初始都为空。执行到最后,我们会发现外部节点桩比内部节点桩多一个节点。考虑以下两种情况。
情况 1 : 若 T 仅有一个节点 v, 我们将 v 取下,并把它放入外部节点桩。因此,外部节点桩有一个节点,而内部节点桩为空。
情况 2: 另外( T 多于一个节点),我们从 T 中取下一个(任意的)外部节点 w 和其父母节点 v, v 为内部节点。我们将 w 放入外部节点桩,将 v 放入内部节点桩。若 v 有父母节点 u, 则将 u 与 w 之前的兄弟节点 z 连接起来,如图 8-10 所示。此次操作取下了一个内部节点 和一个外部节点,并使树变成新的完全二叉树。重复上述操作,我们最后将会得到仅有一个节点的最终树。注意,在经过这样一系列操作并得到最终树的过程中,相同数目的外部节点 和内部节点被分别放入各自的桩中。现在,我们将最终树的节点取下并放入外部节点桩中。因此,外部节点桩比内部节点桩多一个节点
注意:上述关系一般不适用于不完全二叉树和非二叉树,而其他有趣的关系则能适用 (见练习 C-8.32 ~ C-8.34) 。
8.3 树的实现¶
到目前为止,本章所定义的 Tree 和 BinaryTree 类都只是形式上的抽象基类。尽管给出了许多支持操作,但它们都不能直接被实例化。对于树内部如何表示,以及如何高效地在父母节点和孩子节点之间进行切换,我们还没有定义关键的实现细节。特别地,具体实现树要能提供 Root 、parent 、num_ children 、children 和__len__这些方法,对于 BinaryTree 类, 还要提供额外的访问器 left 和 right 。
对于树的内部表示有几种选择。本节介绍最普遍的表示方法。我们先以二叉树为例进行介绍,因为它的形状更有局限性
8.3.1 二叉树的链式存储结构¶
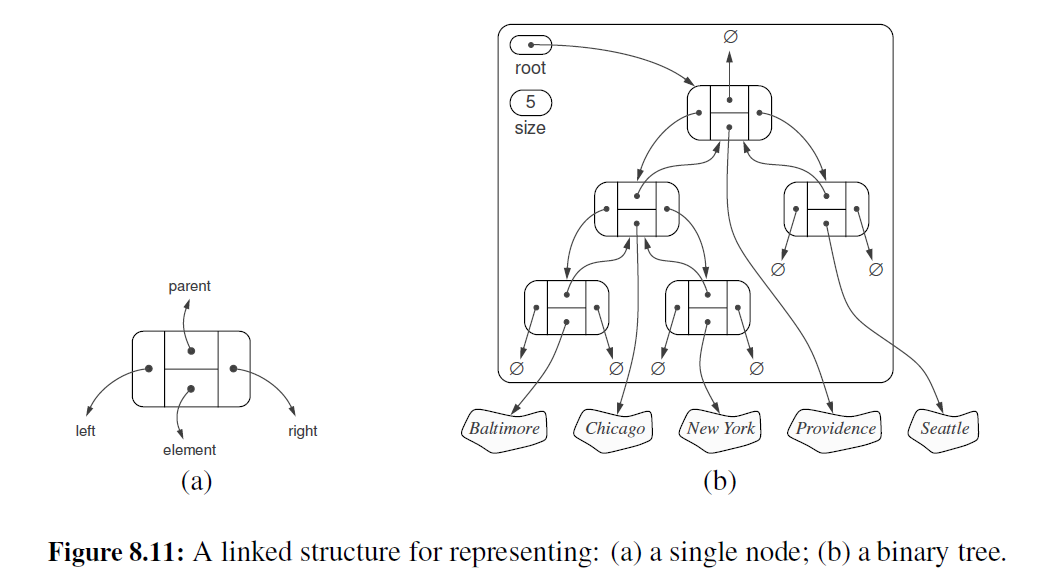
实现二叉树 T 的一个自然方法便是使用链式存储结构,一个节点(见图 8-11a ) 包含多个引用:指向存储在位置 p 的元素的引用,指向 p 的孩子节点和双亲节点的引用。若 p 是 T 的 根节点,则 p 的 parent 字段为 None 。同样,若 p 没有左孩子(或右孩子),则相关字段即为 None 。树本身包含一个实例变量,存储指向根节点(假如存在根节点)的引用,还包含一个 size 变量,表示 T 的所有节点数。在图 8-11b 中,我们给出了表示二叉树的链式存储结构
链式二叉树结构的 python 实现¶
在本节中,我们定义 BinaryTree 类的一个具体子类 LinkedBinaryTree, 该类能够实现二叉树 ADT 。通用方法非常类似于 7.4 节中开发 PositionalList 时所采用的方法:定义一个简单、非公开的_Node 类表示一个节点,再定义一个公开的 Position 类用于封装节点。我们提供_validate 方法,在所给的 position 实例未封装前,能够强有力地验证该实例的有效性。另外,我们也提供_make_position 方法,把节点封装进 position 实例,并返回给调用者。
代码段 8-8 给出了这些定义。从形式上说,新的 Position 类被声明为直接继承 BinaryTree.Position 类。而从技术上说, BinaryTree 类的定义(见代码段 8-7 ) 并未正式声明这样的一个内嵌类,它仅仅平凡地继承于 Tree.Position 。这样设计的一个细微优势在于: Position 类能够继承 __ne__ 这一特殊方法, 以至于相对于 __eq__方法,语句 p != q 能够自然地 执行。
from .binary_tree import BinaryTree
class LinkedBinaryTree(BinaryTree):
"""Linked representation of a binary tree structure."""
#-------------------------- nested _Node class --------------------------
class _Node:
"""Lightweight, nonpublic class for storing a node."""
__slots__ = '_element', '_parent', '_left', '_right' # streamline memory usage
def __init__(self, element, parent=None, left=None, right=None):
self._element = element
self._parent = parent
self._left = left
self._right = right
#-------------------------- nested Position class --------------------------
class Position(BinaryTree.Position):
"""An abstraction representing the location of a single element."""
def __init__(self, container, node):
"""Constructor should not be invoked by user."""
self._container = container
self._node = node
def element(self):
"""Return the element stored at this Position."""
return self._node._element
def __eq__(self, other):
"""Return True if other is a Position representing the same location."""
return type(other) is type(self) and other._node is self._node
#------------------------------- utility methods -------------------------------
def _validate(self, p):
"""Return associated node, if position is valid."""
if not isinstance(p, self.Position):
raise TypeError('p must be proper Position type')
if p._container is not self:
raise ValueError('p does not belong to this container')
if p._node._parent is p._node: # convention for deprecated nodes
raise ValueError('p is no longer valid')
return p._node
def _make_position(self, node):
"""Return Position instance for given node (or None if no node)."""
return self.Position(self, node) if node is not None else None
在代码段 8-9 中,对类继续定义了构造函数,并且对 Tree 和 BinaryTree 类的抽象方法做了具体实现。构造函数通过将 _root 初始化为 None 、将_size 初始化为 0, 能够 建一棵空树。实现访问方法时,谨慎使用了_validate 和_make_position, 防止出现边界问题。
#-------------------------- binary tree constructor --------------------------
def __init__(self):
"""Create an initially empty binary tree."""
self._root = None
self._size = 0
#-------------------------- public accessors --------------------------
def __len__(self):
"""Return the total number of elements in the tree."""
return self._size
def root(self):
"""Return the root Position of the tree (or None if tree is empty)."""
return self._make_position(self._root)
def parent(self, p):
"""Return the Position of p's parent (or None if p is root)."""
node = self._validate(p)
return self._make_position(node._parent)
def left(self, p):
"""Return the Position of p's left child (or None if no left child)."""
node = self._validate(p)
return self._make_position(node._left)
def right(self, p):
"""Return the Position of p's right child (or None if no right child)."""
node = self._validate(p)
return self._make_position(node._right)
def num_children(self, p):
"""Return the number of children of Position p."""
node = self._validate(p)
count = 0
if node._left is not None: # left child exists
count += 1
if node._right is not None: # right child exists
count += 1
return count
更新链式二叉树的操作¶
至此,我们已经给出了用于操作已存在二叉树的函数。而 LinkedBinaryTree 类的构造函数创建了一棵空树,我们没有提供任何改变这种结构的方法,也没有提供任何填充这棵树的方法。
在 Tree 和 BinaryTree 抽象基类中,我们没有声明更新方法的原因如下。
首先,虽然封装原则表明类的外部行为不需要依赖于类的内部实现,而操作的效率却极大地取决于实现方式。我们更倾向于 Tree 类的每个具体实现都能提供更合适的选择方式来更新一棵树。
其次,我们可能不希望更新方法成为公开接口。树有许多应用,适用于其中一个应用的更新操作可能不被另一个应用所接受。而假如我们在基类中声明更新方法,继承于该基类的任何子类都将继承这一方法。例如,考虑方法 T.replace(p, e) 的可能性,该方法用元 素 e 替换存储于位置 p 的元素。这种一般性的方法可能不适用于算术表达式树(见例题 8-7, 在 8.5 节中,我们将会学习另一个例子)的情形,因为我们可能会强制内部节点仅存储一个运算符。
对于链式二叉树,支持日常使用的合理更新方法如下:、
T.add_root(e): 为空树创建根节点,存储元素 e, 并返回根节点的位置。若树非空, 则抛出错误。T.add_ left(p, e):创建新的节点,存储元素 e, 将该节点链接为位置 p 的左孩子,返回结果位置。若 p 已经有左孩子,则抛出错误。T.add_right(p, e):创建新的节点,存储元素 e, 将该节点链接为位置 p 的右孩子,返回结果位置; 若 p 已经有右孩子,则抛出错误。T.replace(p, e):用元素 e 替换存储在位置 p 的元素,返回之前存储的元素。T.delete(p):移除位置为 p 的节点,用它的孩子代替自己,若有,则返回存储在位置 p 的元素; 若 p 有两个孩子,则抛出错误。T.attach(p, T1, T2):将树 T1, T2 分别链接为 T 的叶子节点 p 的左右子树,并将 T1 和 T2 重置为空树;若 p 不是叶子节点,则抛出错误
之所以专门选择这组操作,是因为使用链接表示时,每个操作的最坏运行时间为 O(1) 。
其中最复杂的操作是 delete 和 attach 操作,因为要分析有关的各种双亲-孩子关系的问题和边界条件问题,还要保证执行固定的操作数。(类似于对位置列表的处理,若使用树的前哨节点表示法,则这两种方法的实现过程将大大简化,见练习 C-8.40 。) 为了避免不必要的更新方法被 LinkedBinaryTree 的子类所继承,我们选择所有方法均不采用公开支待的实现方式。换言之,我们对每种方法都提供非公开的形式,例如,使用带下划线的_delete 方法来替换公开的 delete 方法。代码段 8-10 和代码段 8-11 给出了 6 种更新 方法的实现方式。
#-------------------------- nonpublic mutators --------------------------
def _add_root(self, e):
"""Place element e at the root of an empty tree and return new Position.
Raise ValueError if tree nonempty.
"""
if self._root is not None:
raise ValueError('Root exists')
self._size = 1
self._root = self._Node(e)
return self._make_position(self._root)
def _add_left(self, p, e):
"""Create a new left child for Position p, storing element e.
Return the Position of new node.
Raise ValueError if Position p is invalid or p already has a left child.
"""
node = self._validate(p)
if node._left is not None:
raise ValueError('Left child exists')
self._size += 1
node._left = self._Node(e, node) # node is its parent
return self._make_position(node._left)
def _add_right(self, p, e):
"""Create a new right child for Position p, storing element e.
Return the Position of new node.
Raise ValueError if Position p is invalid or p already has a right child.
"""
node = self._validate(p)
if node._right is not None:
raise ValueError('Right child exists')
self._size += 1
node._right = self._Node(e, node) # node is its parent
return self._make_position(node._right)
def _replace(self, p, e):
"""Replace the element at position p with e, and return old element."""
node = self._validate(p)
old = node._element
node._element = e
return old
def _delete(self, p):
"""Delete the node at Position p, and replace it with its child, if any.
Return the element that had been stored at Position p.
Raise ValueError if Position p is invalid or p has two children.
"""
node = self._validate(p)
if self.num_children(p) == 2:
raise ValueError('Position has two children')
child = node._left if node._left else node._right # might be None
if child is not None:
child._parent = node._parent # child's grandparent becomes parent
if node is self._root:
self._root = child # child becomes root
else:
parent = node._parent
if node is parent._left:
parent._left = child
else:
parent._right = child
self._size -= 1
node._parent = node # convention for deprecated node
return node._element
def _attach(self, p, t1, t2):
"""Attach trees t1 and t2, respectively, as the left and right subtrees of the external Position p.
As a side effect, set t1 and t2 to empty.
Raise TypeError if trees t1 and t2 do not match type of this tree.
Raise ValueError if Position p is invalid or not external.
"""
node = self._validate(p)
if not self.is_leaf(p):
raise ValueError('position must be leaf')
if not type(self) is type(t1) is type(t2): # all 3 trees must be same type
raise TypeError('Tree types must match')
self._size += len(t1) + len(t2)
if not t1.is_empty(): # attached t1 as left subtree of node
t1._root._parent = node
node._left = t1._root
t1._root = None # set t1 instance to empty
t1._size = 0
if not t2.is_empty(): # attached t2 as right subtree of node
t2._root._parent = node
node._right = t2._root
t2._root = None # set t2 instance to empty
t2._size = 0
在特定的应用程序中, LinkedBinaryTree 的子类能调用内部非公开的方法,并提供适用于应用程序的公开接口。子类也可以使用公开方法封装一个或多个非公开更新方法供用户调用。我们将会在练习 R-8.15 中要求定义 MutableLinkedBinaryTree 这一子类,该子类能够提供封装 6 种公开更新方法的任意一种。
链式二叉树实现方式的性能¶
为了总结链式结构表示法的效率,我们分析 LinkedBinaryTree 方法的运行时间,其中包括从 Tree 和 BinaryTree 类派生的方法:
- len 方法,在 LinkedBinaryTree 内部实现,使用一个实例变量存储 T 的节点数,花费 O(1) 的时间。is_empty 方法继承自 Tree 类,对 len 方法进行一次调用,因此需要花费 O(1) 的时间。
- 访问方法 root 、left 、right 、parent 和 num_children 直接在 LinkedBinaryTree 中执行, 花费 O(1) 的时间。sibling 和 children 方法从 BinaryTree 类派生,对其他访问方法做固定次的调用,因此,它们的运行时间也是 O(1) 。
- Tree 类的
is_root和is_leaf方法都运行 O(1) 的时间, 因为is_root调用root方法,之后判定两者的位置是否相等;而 is_leaf 调用 left 和 right 方法,并验证二者是否返回 None" - depth 和 height 方法在 8.1.3 节中己做过分析。depth 方法在位置 p 处运行 O(\(d_p+1\) ) 的时间,其中 \(d_p\) 是它的深度; height 方法在树的根节点处运行 O(n) 的时间。
- 各种更新方法
add_root、add_left、add_right、replace、delete和attach(即它们的非公开实现方式)都运行 O(1) 的时间, 因为它们每次操作都仅仅重新链接到固定的节点数。
表 8-1 总结了二叉树链式存储结构实现方式的性能

8.3.2 基于数组表示的二叉树¶
二叉树 T 的一种可供选择的表示法是对 T 的位置进行编号。对于 T 的每个位置 p, 设 \(f(p)\) 为整数且定义如下:
- 若 p 是 T 的根节点,则 \(f(p)=0\) 。
- 若 p 是位置 q 的左孩子,则 \(f(p)=2f(q) + 1\) 。
- 若 p 是位置 q 的右孩子,则 \(f(p)=2f(q) + 2\) 。
编号函数 \(f\) 被称为二叉树 T 的位置的层编号,因为它将 T 每一层的位置从左往右按递增顺序编号(见图 8-12 ) 。注意,层编号是基于树内的潜在位置,而不是所给树的实际位置, 因此编号不一定是连续的。例如,在图 8-12b 中,没有层编号为 13 或 14 的节点,因为层编 号为 6 的节点没有孩子
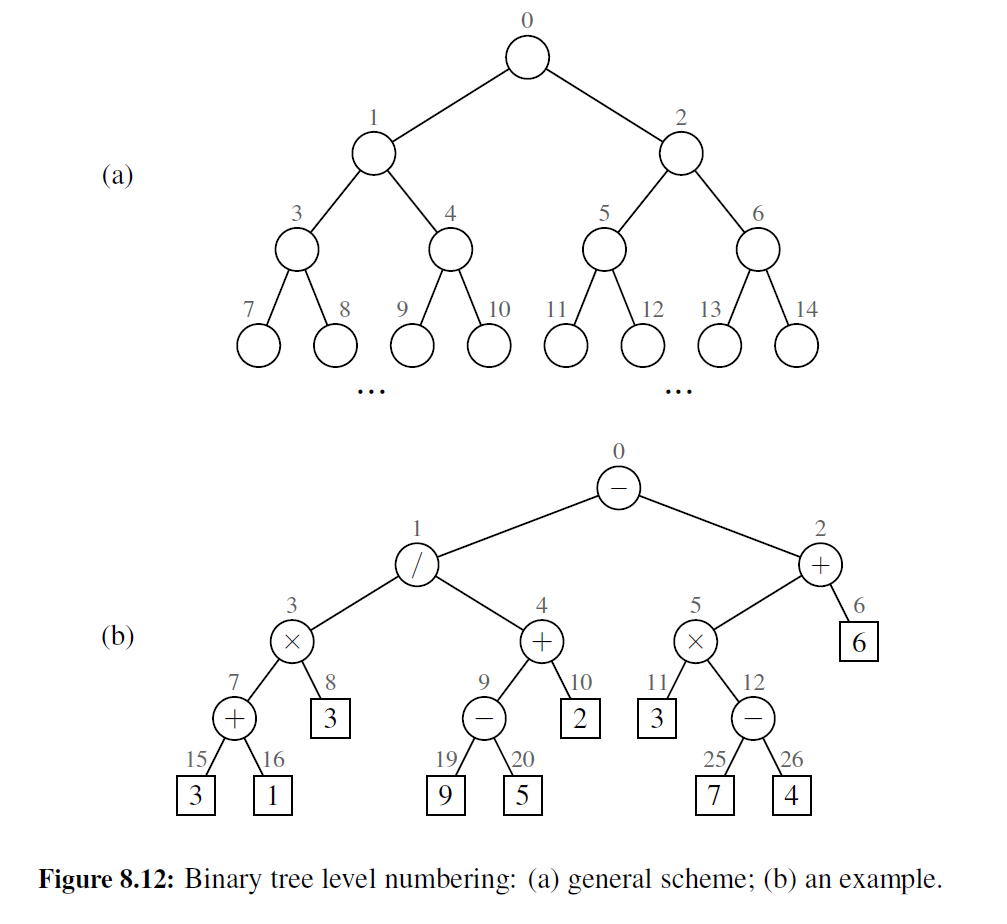
层编号函数 \(f\) 是一种二叉树 T 依据基于数组结构 A (例如, python 列表) 的表示方法, T 的 p 位置元素存储在数组下标为 \(f(p)\) 的 内存中。在图 8-13 中,我们给出了一个二叉树基于数组表示的例子。
二叉树基于数组的表示方式的一个优势在于位置 p 能用简单的整数 \(f(p)\) 来表 示, 且基于位置的方法(如 root 、parent 、 left 和 right 方法)能采用对编号 \(f(p)\) 进行简单算术操作的方法来执行。根据层编号的公式, p 左孩子的下标为 \(2f(p) + 1\),右孩子的下标为 \(2f(p)+2\), 而 p 父母的下标为 \(\left\lfloor f(p)-1/2\right\rfloor\)。我们将完整实现方式的细节留作练习 R-8.18
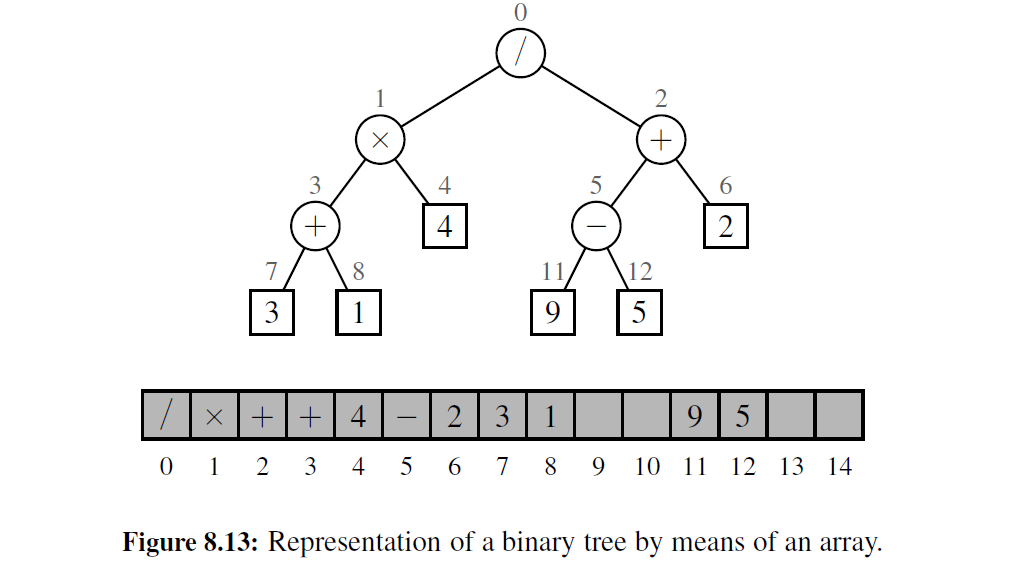
基于数组表示的空间使用情况极大地依赖于树的形状。设 n 为树 T 的节点数,\(f_M\) 为 \(f(p)\) 对于 T 所有节点的最大值。数组 A 所需长度为\(N= 1 +f_M\),因为元素范围为从 A[0] 到 A[\(f_M\)] 。
注意, A 可以有多个空单元,同时这些空单元也未指向 T 的已有节点。事实上, 在最坏情况下, \(N=2^n-1\), 证明过程留作练习 R-8.16 。在 9.3 节中,我们将学习二叉树的 heaps 类,其中 N = n 。因此, 即使是最坏情况下的空间使用,仍有应用程序指明二叉树的数组表示是空间高效的。而对于 一般的二叉树而言,这种表示方式的指数级最坏空间需求是不允许的。
数组表示的另一个缺点是不能有效地支持树的一些更新方法,例如删除节点且提升自己的孩子节点的编号需要花费 O(n) 的时间,因为在数组中,不仅有孩子节点需要移动位置, 该孩子节点的所有子孙也都要移动。
8.3.3 一般树的链式存储结构¶
当使用链式存储结构表示二叉树时,每个节点都明确包含了 left 和 right 字段,用于指向各自的孩子节点。对于一般树, 一个节点所拥有的孩子节点之间没有优先级限制。使用链式存储结构实现一般树 T 的一个很自然的方法是:使每个节点都配置一个容器,该容器存储指向每个孩子的引用。例如,节点的 children 字段可以是一张 python 列表,用于存储指向该节点孩子(若有) 的引用。图 8-14 阐明了这种链式表示
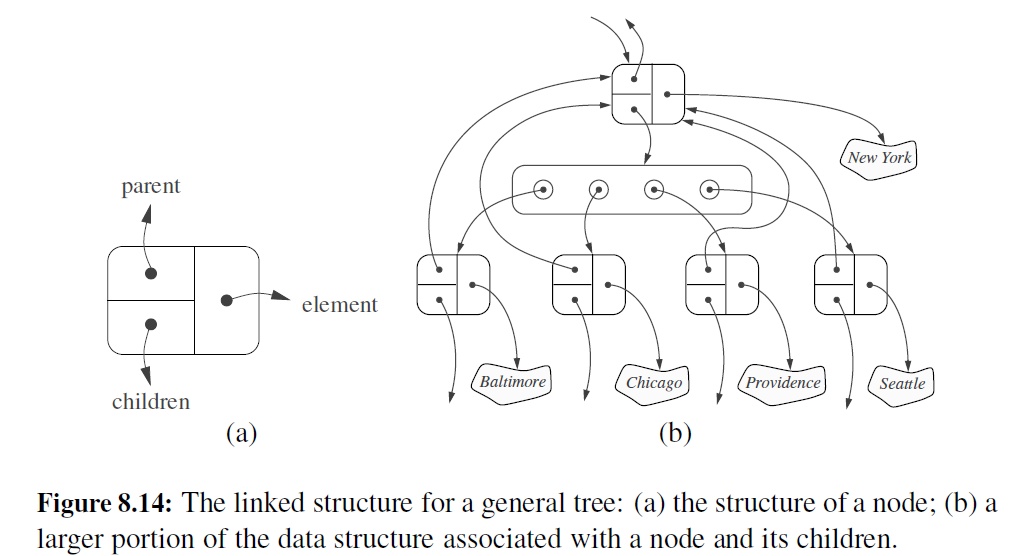
表 8-2 总结了使用链式存储结构实现一般树的性能。分析过程留作练习 R-8.14 , 但需要注意,使用集合存储每个位置 p 的孩子时,我们可以使用简单的迭代来实现 children(p)

表 8-2 使用链式存储结构实现的具有 n 个节点的一般树的各种访问方法的运行时间。我们设 \(c_p\) 表示位置 p 的孩子节点数。空间占用为 O(n)
8.4 树的遍历算法¶
树 T 的遍历是访问或者 “拜访" T 的所有位置的一种系统化方法。"访问“ p 位置的相关具体行动取决于遍历的应用程序,并且可能包括任何计数器为 p 执行一些复杂的运算。在本节中,我们描述了几种常见的树的遍历方案,并在各种树类的环境中实现它们,还讨论了几种树遍历的常见应用。
8.4.1 树的先序和后序遍历¶
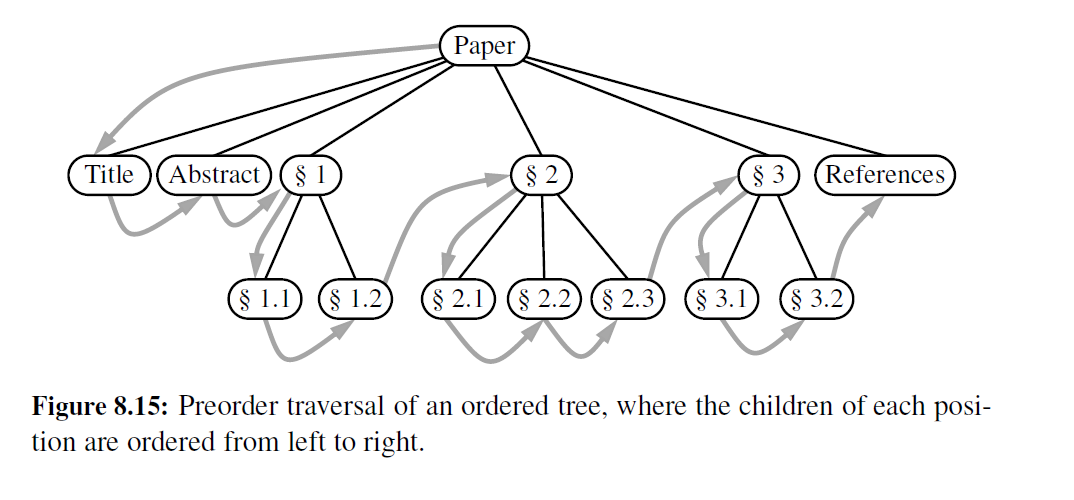
在树 T 的先序遍历中,首先访间 T 的根,然后递归地访问子树的根。如果这棵树是有序的,则根据孩子的顺序遍历子树。对于 p 位置处子树的根的先序遍历,其伪代码如代码段 8-12 所示
Algorithm preorder(T, p):
perform the “visit” action for position p
for each child c in T.children(p) do
preorder(T, c) {recursively traverse the subtree rooted at c}
后序遍历 另一个重要的树的遍历算法是后序遍历。在某种程度上,这种算法可以看作相反的先序遍历,因为它优先遍历子树的根,即首先从孩子的根开始,然后访问根(因此叫作后序) 。后序遍历的伪代码如代码段 8-13 所示,图 8-16 描绘了一个后序遍历的例子。
Algorithm postorder(T, p):
for each child c in T.children(p) do
postorder(T, c) {recursively traverse the subtree rooted at c}
perform the “visit” action for position p
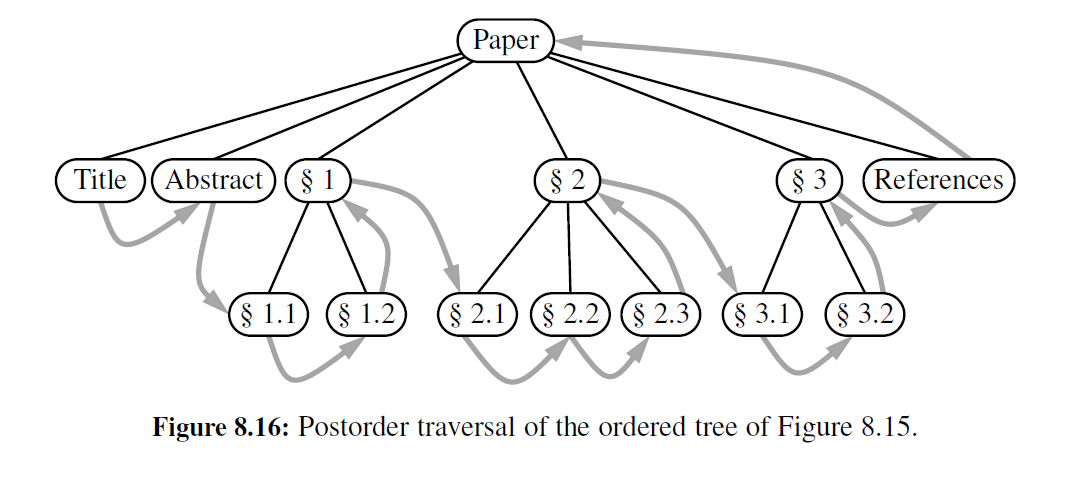
从伪代码来看,先序遍历和后序遍历的递归过程是一样的(均是从树的上方(根)往下方(叶)遍历),区别只在于是在进行递归前访问还是在递归后访问,如果在递归前访问,那么无论后面的递归过程有无执行,这次访问都已经成功了(这因此是尾递归);而如果在递归后访问,那么最先被访问的节点是叶,根节点(或者子树的根节点)需要整个递归完成以后才能被访问
运行时间分析¶
先序遍历和后序遍历的算法对于访问树的所有位置都是有效的,对这两种算法的分析和 hight2 算法是相似的,如 8.1.3 节的代码段 8-5 所示。在每个 p 位置,遍历算法中的非递归部分所需的时间为 O(\(c_p+ 1\)), \(c_p\) 是指 p 位置处孩子的个数,假设访问本身需要 O(1) 的时间。 由命题 8-5 可知,树 T 的整体运行时间为 O(n) ,其中 n 是树中位置的数量。这个运行时间是最佳的,因为遍历必须经过树的 n 个位置。
8.4.2 树的广度优先遍历¶
在访问树的位置时先序遍历和后序遍历是常见的方法,另一种常见的是遍历树的方法是在访问深度 d 的位置之前先访问深度 d + 1 的位置。这种算法称为广度优先遍历。
广度优先遍历广泛应用于游戏软件上,在游戏(或计算机)中,博弈树代表了可选择的一些动作,树的根是游戏的初始配置。例如,图 8-17 所示即为井字棋的部分博弈树。
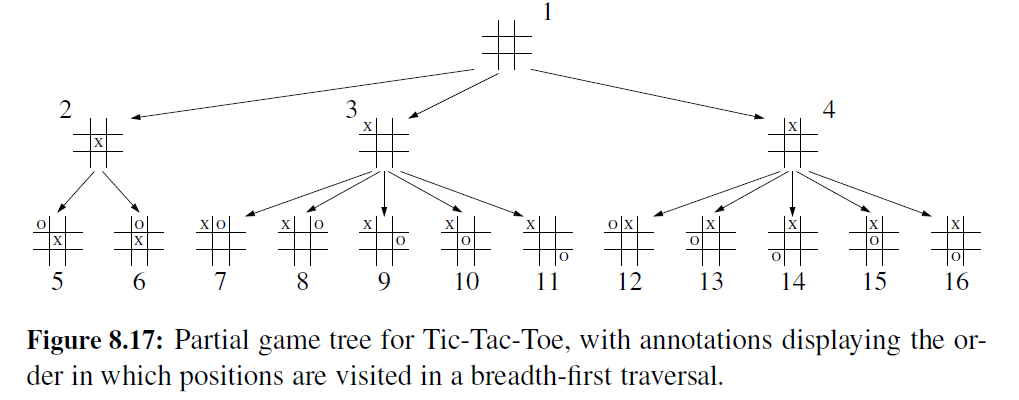
之所以常执行这样一个博弈树的广度优先遍历,是因为计算机无法在有限的时间内去挖掘完整的博弈树。所以计算机要考虑所有动作,然后在允许的计算时间内对这些动作进行回馈。
广度遍历的伪代码如代码段 8-14 所示。这个过程不是递归的,因为我们不是首先遍历整个子树。我们使用一个队列来产生 FIFO (即先进先出)访问节点的顺序语义。整体的运行时间为 O(n) ,因为对 enqueue 和 dequeue 操作各调用了 n 次。
Algorithm breadthfirst(T):
Initialize queue Q to contain T.root( )
while Q not empty do
p = Q.dequeue( ) {p is the oldest entry in the queue}
perform the “visit” action for position p
for each child c in T.children(p) do
Q.enqueue(c) {add p’s children to the end of the queue for later visits}
8.4.3 二叉树的中序遍历¶
前面介绍的对于一般树的标准先序、后序和广度的优先遍历能直接应用在二叉树中。在这节中,我们介绍另一种常见的专门应用于二叉树的遍历算法。
在中序遍历中,我们通过递归遍历左右子树去访问一个位置。二叉树的中序遍历可以看作 “从左到右“ 非正式地访问 T 的节点。事实上,对于每个位置 p, p 将在其左子树之后及其右子树之前被中序遍历访问。中序遍历算法的伪码如代码段 8-15 所示。图 8-18 描述了中序遍历的一个例子
Algorithm inorder(p):
if p has a left child lc then
inorder(lc) {recursively traverse the left subtree of p}
perform the “visit” action for position p
if p has a right child rc then
inorder(rc) {recursively traverse the right subtree of p}
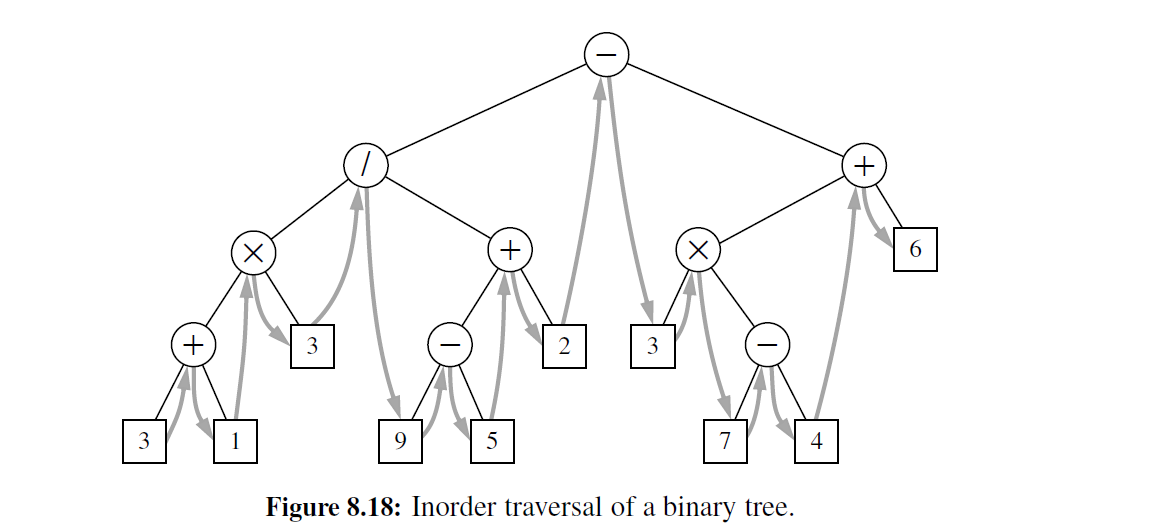
如同我们在二路递归中所谈到的一样,在执行程序语句时是按从上到下的顺序来进行的,因此以根节点为例来解释中序遍历
- 如果根节点的孩子节点一直包含左孩子节点,那么根节点在左孩子节点被访问完成前,一直都不会被访问
- 直到递归到最后一个包含左孩子节点的节点,那么该节点的左和右(如果有的话)孩子节点将会被先后访问,此时开始往回进行访问操作(相对根节点在左侧的节点将均会以该顺序被访问)
- 此时根节点会在相对根节点在左侧所有的节点被访问后被访问
- 接着以相同的顺序来访问相对根节点在右侧的节点
中序遍历的算法有几个重要的应用。使用二叉树表示一个算术表达式,如图 8-18 所示, 中序遍历访问的位置与标准的顺序表达式的顺序一致,例如 \(3 + 1\times 3/9 - 5 + 2 …\)(尽管没有括号) 。
二叉搜索树¶
中序遍历算法的一个重要应用是把有序序列的元素存储在二叉树中,所定义的这种结构称为二叉搜索树。设 S 为 一个集合,其独特的元素存在次序关系。例如, S 可能是一组整数。S 的二叉搜索树是 T, 对于 T 的每一个位置 p ,有:
- 位置 p 存储 S 的一个元素,记作 e(p) 。
- 存储在 p 的左子树的元素(如果有的话)小于 e(p) 。
- 存储在 p 的右子树的元素(如果有的话)大于 e(p) 。
图 8-19 所示为二叉搜索树的例子。上述性能保证二叉搜索树 T 的中序遍历可以按照非递减次序访问元素
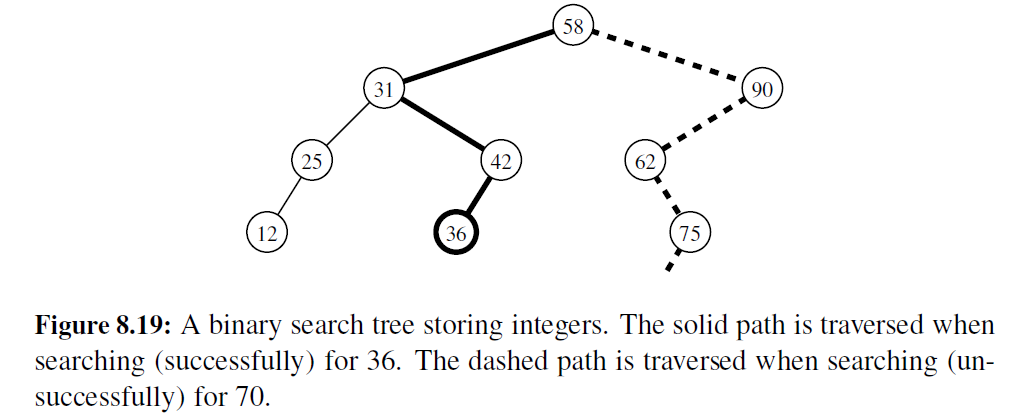
我们可以为 S 使用二叉搜索树 T, 来寻找 S 中的元素 v, 从根开始遍历树 T 下的路径。在 p 遇到的每个内部位置, 我们比较搜索值 v 和存储在 p 位置的 e(p) 。如果 v
注意,二叉搜索树 T 的运行时间是和 T 的高度成正比的。回忆命题 8-8, n 个节点二叉树的高度可以小到 \(\log(n + 1) - 1\) 或者大到 \(n - 1\) 。因此,当二叉树高度最小时是最有效的。第 11 章将主要介绍搜索树。
8.4.4 用 python 实现树遍历¶
在 8.1.2 节中,我们第一次定义树 ADT 。树 T 应该支持下列方法:
- T.positions():树 T 的所有位置生成一个迭代器。
- iter(T) :生成一个迭代器用树 T 存储所有元素。
之前,我们不对这些迭代器报告的结果的顺序做任何假设。在本节中,我们将演示如何让任意一种之前介绍的树遍历算法都能用于产生这些迭代。
一开始,我们注意到树的所有元素很容易产生一个迭代器,前提是依赖一个所有位置的假定迭代器。因此,支持 iter(T) 语法可以正式地通过带有抽象基本树类的特殊方法的 iter 的具体实现给出。我们以 python 的生成器语法作为迭代产生的机制( 见 1.8 节) 。代码段 8-16 给出了 Tree. __iter__ 的实现。
def __iter__(self):
"""Generate an iteration of the tree's elements."""
for p in self.positions(): # use same order as positions()
yield p.element() # but yield each element
为了实现 positions 方法,我们可以选择树遍历算法。考虑到这些遍历顺序的优点, 我们将提供每个策略的独立实现,这些实现可以被类的使用者直接调用。我们可以选择其中一个作为树 ADT 的 positions 方法的默认顺序
先序遍历¶
首先考虑先序遍历的算法。我们通过调用树 T 的 T.preorder() 来给出一个公共的方法, 该方法生成一个关于树的所有位置的先序迭代器。然而,像代码段 8-12 中描述的生成先序遍历的递归算法,必须把树的特定位置参数化来作为子树的根进行遍历。对于这种情况, 一种标准的解决方案是用所需的递归参数化来定义非公开的应用程序方法,然后由公共方法 preoder 在树根上调用非公开方法。这样设计的实现在代码段 8-17 中给出。
def preorder(self):
"""Generate a preorder iteration of positions in the tree."""
if not self.is_empty():
for p in self._subtree_preorder(self.root()): # start recursion
yield p
def _subtree_preorder(self, p):
"""Generate a preorder iteration of positions in subtree rooted at p."""
yield p # visit p before its subtrees
for c in self.children(p): # for each child c
for other in self._subtree_preorder(c): # do preorder of c's subtree
yield other # yielding each to our caller
从形式上讲, preorder 和应用 _subtree_preorder 是生成器。我们把位置给调用者,然后让调用者决定在该位置执行什么操作,而不是在这段代码中执行 “访问“ 行为。
_subtree_preorder 方法是递归的。然而,递归形式略有不同,因为我们依赖于生成器而不是传统的函数。为了生成孩子 c 的子树的所有位置,我们在通过递归调用 self._subtree_ preorder(c) 产生的位置上执行循环,并在外环境中重新生成每个位置。注意,如果 p 是叶 子, self.children(p) 上的 for 循环是 trivial 的(此时我们已经到达了递归的基本情况) 。
什么是生成器(迭代器)?
基于先入为主的思想,我们会把语句
for i in range (100)中的变量
i解释为数组[1,2,…,100],中的一个元素(或者说一个数),但实际上,i是由生成器range(100)“生成“ 的一个变量,在这个语句中,总共会生成 100 次i,每次执行__next__方法就会生成一个新的i(如何生成则取决于内部的 yield 语句)这里就要提到”循环次数“这个暧昧的概念,在我们的成见中,循环是要有一个次数上限的,但实际上在 for 循环中,决定我们口中的所谓”循环次数“的变量是生成器(更具体地说,是内部如何使用 yield 语句),因此,通过对生成器内部的改写,我们可以任意决定所谓的”循环次数“,比如在下面的例子中
我们向生成器输入参数 1,然后输出了十个参数,在这个过程中,
i(外部语句中)的值不断改变,最终变为 9因此 for 语句并非完全是用来进行循环的,或者说循环只是其功能最普遍的一部分,更重要的应用是根据生成器的规则来迭代变量
i
我们用相似的技巧从树的根部应用公共的 preorder 方法重新生成所有位置。如果树是空的,什么都不产生。在这点上,我们为 preorder 迭代器提供全面支持, 所以类的用户可以编写代码如下:
for p in T.preorder()
# "visit" position p
官方树 ADT 要求所有树支持 positions 方法。为了用先序遍历作为默认的迭代顺序,我们在代码段 8-18 中给出了 Tree 类的定义。我们返回整个迭代作为对象, 而不是通过先序调用循环返回结果。
def positions(self):
"""Generate an iteration of the tree's positions."""
return self.preorder() # return entire preorder iteration
后序遍历¶
我们可以应用与先序遍历相似的技巧来实现后序遍历。唯一不同的是后序递归应用,直到递归地产生子树的位置之后,才生成位置 p 。代码段 8-19 给出了一个实例。
def postorder(self):
"""Generate a postorder iteration of positions in the tree."""
if not self.is_empty():
for p in self._subtree_postorder(self.root()): # start recursion
yield p
def _subtree_postorder(self, p):
"""Generate a postorder iteration of positions in subtree rooted at p."""
for c in self.children(p): # for each child c
for other in self._subtree_postorder(c): # do postorder of c's subtree
yield other # yielding each to our caller
yield p # visit p after its subtrees
在遍历完成以前,yield p 语句不会被执行,在遍历完成后则会递归的向上执行
广度优先遍历¶
在代码段 8-20 中,我们给出了一个在 Tree 类的上下文中执行广度优先遍历的实现。广度优先遍历算法不是递归的,它借助位置队列来管理递归程序。尽管任何队列 ADT 的实现对这个例子而言都足够了,但从 7.1.2 节开始,我们用 LinkedQueue 类来实现。
def breadthfirst(self):
"""Generate a breadth-first iteration of the positions of the tree."""
if not self.is_empty():
fringe = LinkedQueue() # known positions not yet yielded
fringe.enqueue(self.root()) # starting with the root
while not fringe.is_empty():
p = fringe.dequeue() # remove from front of the queue
yield p # report this position
for c in self.children(p):
fringe.enqueue(c) # add children to back of queue
中序遍历二叉树¶
先序、后序和广度优先遍历算法可应用于所有树,所以我们在 Tree 的抽象基类中包含了 它们的所有实现。这些方法可以被抽象二叉树类、具体的链二叉树类和其他派生的类继承。
由于中序遍历算法显式地依赖于左和右孩子节点的概念,只适用于二叉树,因此我们在 BinaryTree 类的结构体中包含了该算法的定义。我们使用一个与先序和后序遍历相似的技巧实现中序遍历(见代码段 8-21) 。
def inorder(self):
"""Generate an inorder iteration of positions in the tree."""
if not self.is_empty():
for p in self._subtree_inorder(self.root()):
yield p
def _subtree_inorder(self, p):
"""Generate an inorder iteration of positions in subtree rooted at p."""
if self.left(p) is not None: # if left child exists, traverse its subtree
for other in self._subtree_inorder(self.left(p)):
yield other
yield p # visit p between its subtrees
if self.right(p) is not None: # if right child exists, traverse its subtree
for other in self._subtree_inorder(self.right(p)):
yield other
对于二叉树的许多应用, 中序遍历提供了自然的迭代。我们可以通过重写继承自 Tree 类的 positions 方法来将其作为 BinaryTree 类的默认值( 见代码段 8-22 ) 。
# override inherited version to make inorder the default
def positions(self):
"""Generate an iteration of the tree's positions."""
return self.inorder() # make inorder the default
8.4.5 树遍历的应用¶
在本节中, 我们将演示几个树遍历的代表应用程序,其中包括一些标准遍历算法的定制。
目录表¶
我们使用树来表示文档的层次结构,树的先序遍历可以自然地被用于产生一个文档的目录表。例如, 图 8-15 中与树相关联的目录表如图 8-20 所示。图 8-20a 按每行一个元素的样式进行了简单表示。图 8-20b 则基于树的深度,通过缩进元素给出了一种更醒目的表示形式。
类似的表示可用于展示计算机文件系统目录(见图 8-3 ) 。

给定树 T 没有缩进版本的目录表,可以用下面的代码:
for p in T.preorder():
print(p.element())
为了生成图 8-20b 的表示样式,我们将每个元素的空间缩进树中元素深度的 2 倍( 因此根元素是不被缩进的) 。尽管我们可以替换语句打印的循环体( 2 * T.depth(p) * ' ' + str(p .element())) , 但这种方法会造成不必要的效率低下。基于 8.4.1 节的分析, 虽然产生的先序遍历运行时间为 O(n) ,调用深度会产生一个隐含的成本。从树的每一个位置调用深度都会产生最坏运行时间 O(\(n^2\)) ,如 8.1.3 节中 hight1 算法的分析。
生成一个缩进目录表的首选方法是重新设置一个自顶向下的递归,其中将当前的深度作为额外的参数。代码段 8-23 给出了这个实现。这个实现最坏的运行时间为 O(n) (除去技术上将花费打印增加长度的字符串的时间) 。
def preorder_indent(T, p, d):
"""Print preorder representation of subtree of T rooted at p at depth d."""
print(2*d*' ' + str(p.element())) # use depth for indentation
for c in T.children(p):
preorder_indent(T, c, d+1) # child depth is d+1
考虑图 8 -20 所示的例子,幸运的是编号是嵌入树中的元素。一般来讲,我们可能有兴趣用先序遍历展示树的结构,缩进和树上没有显式呈现的编号。例如,我们可以按照以下样式开始展示图 8-2 所示的树。

这更具有挑战性,因为数字被用作标签隐含在树的结构中。标签取决于位置的索引,相对于其兄弟姐妹,沿着路径从根到当前位置。为了实现这个任务,我们将路径作为一个额外的参数添加到递归签名。尤其是,我们使用一个 0 索引数字列表,其每个位置沿着向下的路径, 而不是根( 我们将这些数据转换成索引形式打印) 。
在实现层级,我们希望在将一个新参数从递归的一个层级传递到下一个层级时,避免这样低效率的列表。一个标准的解决方案是通过递归共享相同的列表实例。在递归的层级上, 一个新的条目在做进一步递归调用之前被暂时添加到列表的末尾。为了 “不留下痕迹”,相同的代码块在完成任务之前必须移除多余的条目。代码段 8-24 给出了基于这种方法的实现。
def preorder_label(T, p, d, path):
"""Print labeled representation of subtree of T rooted at p at depth d."""
label = '.'.join(str(j+1) for j in path) # displayed labels are one-indexed
print(2*d*' ' + label, p.element())
path.append(0) # path entries are zero-indexed
for c in T.children(p):
preorder_label(T, c, d+1, path) # child depth is d+1
path[-1] += 1
path.pop()
树的附加说明表示¶
如图 8-20a 所示,如果只给定元素的先序序列,那么不可能重建一般的树。要更好地定义树的结构, 一些附加的上下文是必需的。用缩进或者编了号的标签提供这样的环境是非常人性化的表现。不管怎样,有些更简明的树的字符串是对计算机友好的。
在本节中,我们探索这样一个表示。树 T 的附加说明的字符串表示 P(T) 以如下方式递归定义。如果 T 由单一的位置 p 组成,则
P(T) = str(p.element()).
否则,它被递归地定义为,
P(T) = str(p.element())+ '(' +P(T1)+ ',' '+ · · · +' , '+P(Tk)+ ')'
其中 p 是 T 的根, \(T_1,T_2,...,T_k\) 是 p 的孩子的子树根。如果 T 是有序树,则按序给出。我们用 “+” 来表示字符串连接。例如,图 8-2 所示的树的附加说明表示如下(换行符是修饰):

虽然附加说明本质上是一个先序遍历,但是我们不能用之前代码段 8-17 给出的 preorder 实现轻易生成额外的标点符号。左括号必须在循环该位置的孩子之前产生,右括号必须在循环该位置的孩子之后产生。进一步来讲,逗号必须产生。python 函数 parenthesize 是一个自定义的遍历,用于输出树 T 的附加说明字符串表示,如代码段 8-25 所示
def parenthesize(T, p):
"""Print parenthesized representation of subtree of T rooted at p."""
print(p.element(), end='') # use of end avoids trailing newline
if not T.is_leaf(p):
first_time = True
for c in T.children(p):
sep = ' (' if first_time else ', ' # determine proper separator
print(sep, end='')
first_time = False # any future passes will not be the first
parenthesize(T, c) # recur on child
print(')', end='') # include closing parenthesis
计算磁盘空间¶
在例 8-1 中,我们用树作为文件系统结构的模型,用内部位置代表目录,用叶子代表文件。事实上,在第 4 章中介绍递归的使用时,我们专门研究过文件系统(见 4.1.4 节) 。虽然当时没有明确地将文件系统模型化为一棵树,但我们给出了计算磁盘使用率的一个算法的实 现(见代码段 4-5 ) 。
磁盘空间的递归计算是后序遍历的一个象征,正如我们不能有效地计算总的使用空间直 到了解子目录的使用空间之后。不幸的是,代码段 8-19 给出的 postorder 的正式实施并不满足这一目的。访问一个目录的位置时,没有简单的方法来辨别之前的哪个位置代表孩子的目 录, 也无法辨别有多少递归磁盘空间被分配。
我们想要将孩子向父亲返回信息的机制作为遍历过程的一部分。每层递归为调用者提供一个返回值, 来自定义解决磁盘空间问题,如代码段 8-26 所示
def disk_space(T, p):
"""Return total disk space for subtree of T rooted at p."""
subtotal = p.element().space() # space used at position p
for c in T.children(p):
subtotal += disk_space(T, c) # add child's space to subtotal
return subtotal
8.4.6 欧拉图和模板方法模式¶
8.4.5 节描述的各种应用程序展示了树递归遍历的强大功能。不幸的是,它们也表明 Tree 类的 preorder 和 postorder 方法的具体实现,或者 BinaryTree 类的 inorder 方法的实现, 一般不足以采集我们期望的计算范围。在有些情况下,我们需要更多的混合方法,比如在初始工作执行之前重复执行子树,或者在递归执行之后进行一些额外的工作,对于二叉树,工作执行两种可能的递归。进一步来讲,在某些情况下,知道位置的深度,或者从根到该位置的完整的路径,或者返回从递归的一个层级到另一个层级的信息,这些是很重要的。对于前面的每个应用程序,我们可以开发 一个正确适用递归思想的实现,但是面向对象编程(见 2.1.1 节)原则包括适应性和可重用性
在本节中,我们开发了一个更通用的框架,即基于概念实现树的遍历——欧拉遍历。一 般树 T 的欧拉遍历可以非正式地定义为沿着 T“ 走”,从根开始 “走“ 向最后一个孩子,我们保持在左边,像 “墙” 一样查看 T 的边缘, 如图 8-21 所示
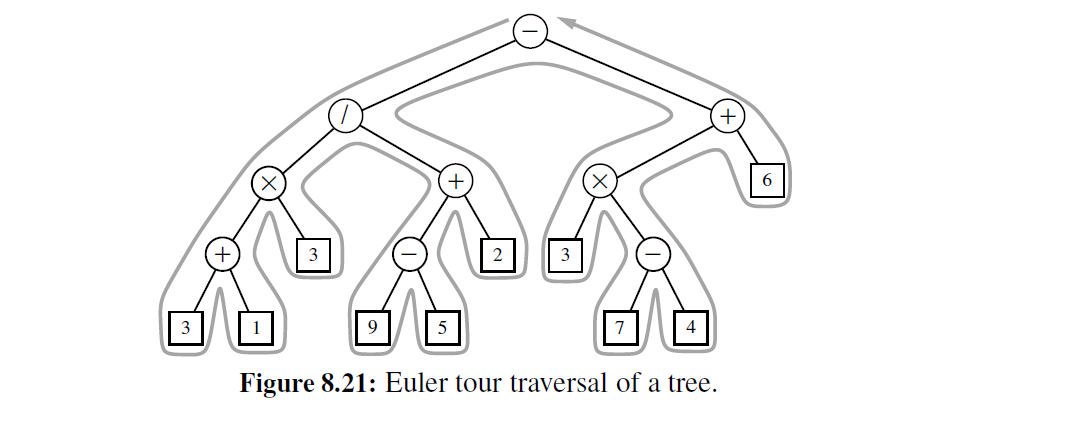
遍历的复杂度为 O(n) ,因为恰好两次沿着树的 n - 1 条边进行——一次沿着边缘向下走, 一次沿右边缘向上走。为了统一先序和后序遍历的概念,对于每个位置 p, 我们可以考虑两个值得注意的"访问 ”:
- 当到达第一个位置,即当遍历立刻通过可视化节点的左边时,“先访问” 出现。
- 当从该位置向上遍历, 即当遍历通过可视化节点的右边时,”后访问“ 发生。
欧拉遍历的过程很容易被看成递归,在给定位置的“先访问”和“后访问”之间将是每个子树的递归遍历。以图 8-21 为例,整个遍历的连续部分本身就是节点带元素 ”/ 的子 的欧拉遍历。遍历包含两个连续的子遍历, 一个遍历左子树, 一个遍历右子树。对于根在 p 位置处的子树的欧拉遍历,其伪代码如代码段 8 -27 所示
Algorithm eulertour(T, p):
perform the “pre visit” action for position p
for each child c in T.children(p) do
eulertour(T, c) {recursively tour the subtree rooted at c}
perform the “post visit” action for position p
模板方法模式¶
为了提供一个可重用的和适应性强的框架,我们借用了一种有趣的面向对象软件设计模式一模板方法模式。模板方法模式通过精简某些步骤描述了一个通用的计算机制。在指定步骤的过程中,为了允许自定义,基本算法调用称为钩子( hook) 的辅助函数。
在欧拉遍历的上下文中,我们定义了两个单独的钩子。在子树被访问之前,“先序访问” 钩子被调用;在子树完成遍历之后,”后续访问''钩子被调用。我们的实现将采用 EulerTour 类管理进程,并简单定义什么也不做的钩子。遍历可以通过定义 EulerTour 的子类和重载一 个或两个用以提供特殊性能的钩子来进行个性化设置
python 实现
代码段 8-28 提供了 EulerTour 类的实现,主要的递归过程被定义为非公开的_tour 方法。通过发送引用一个特定的树的构造函数创建遍历实例,然后通过调用公共执行方法去遍历返回一个计算的最终结果。
class EulerTour:
"""Abstract base class for performing Euler tour of a tree.
_hook_previsit and _hook_postvisit may be overridden by subclasses.
"""
def __init__(self, tree):
"""Prepare an Euler tour template for given tree."""
self._tree = tree
def tree(self):
"""Return reference to the tree being traversed."""
return self._tree
def execute(self):
"""Perform the tour and return any result from post visit of root."""
if len(self._tree) > 0:
return self._tour(self._tree.root(), 0, []) # start the recursion
def _tour(self, p, d, path):
"""Perform tour of subtree rooted at Position p.
p Position of current node being visited
d depth of p in the tree
path list of indices of children on path from root to p
"""
self._hook_previsit(p, d, path) # "pre visit" p
results = []
path.append(0) # add new index to end of path before recursion
for c in self._tree.children(p):
results.append(self._tour(c, d+1, path)) # recur on child's subtree
path[-1] += 1 # increment index
path.pop() # remove extraneous index from end of path
answer = self._hook_postvisit(p, d, path, results) # "post visit" p
return answer
def _hook_previsit(self, p, d, path):
"""Visit Position p, before the tour of its children.
p Position of current position being visited
d depth of p in the tree
path list of indices of children on path from root to p
"""
pass
def _hook_postvisit(self, p, d, path, results):
"""Visit Position p, after the tour of its children.
p Position of current position being visited
d depth of p in the tree
path list of indices of children on path from root to p
results is a list of values returned by _hook_postvisit(c)
for each child c of p.
"""
pass
8.4.5 节的简单应用基于定制遍历的经验,我们在代码段 8-24 中介绍了支持主要的 EulerTour 遍历以维护递归遍历的深度和路径。我们还为递归层级提供了一个机制,用于在进行后续处理时返回值。在形式上, 框架依赖于专业化的两个钩子
method_ hook_previsit(p,d,path)每个位置调用这个函数一次一一在子树遍历之前立即调用(如果有的话) 。参数位置 p 是树上的位置, d 是位置的深度, path 是索引的列表,使用代码段 8-24 中所描述的约定。这个函数没有返回值。method_ hook_postvisit(p,d,path,results)这个函数在每个位置被调用一次一在其子树被遍历后立即调用,前三个参数使用与_hook_previsit相同的约定。最后一个参数是以 p 的子树后序遍历的返回值作为列表对象。任何通过此调用的返回值可以被其父母节点 p 所利用。
对于更复杂的任务,EulerTour 的子类也可以选择以实例变量的形式初始化和维护额外的状态,这些状态可以在钩子的主体内访问。
在基类中,钩子函数并不提供返回值,但在其子类中,可以通过重载钩子函数的方法来添加额外的功能
使用欧拉遍历框架¶
为了展示欧拉遍历的灵活性,我们重新审视 8.4.5 节中的示例应用程序。举一个简单的例子, 一个缩进的先序遍历(类似于代码段 8-23 ),可以由代码段 8-29 中给出的简单子类生成。
class PreorderPrintIndentedTour(EulerTour):
def _hook_previsit(self, p, d, path):
print(2*d*' ' + str(p.element()))
对于给定的树 T, 通过创建子类的实例来开始遍历并调用 execute 方法。代码如下:
tour = PreorderPrintlndentedTour(T)
tour.execute()
缩进标记版本类似于代码段 8-24, 可能通过 EulerTour 的新子类生成,如代码段 8-30 所示。
class PreorderPrintIndentedLabeledTour(EulerTour):
def _hook_previsit(self, p, d, path):
label = '.'.join(str(j+1) for j in path) # labels are one-indexed
print(2*d*' ' + label, p.element())
为了生成附加说明的字符串表示,最初实现如代码段 8-25 所示,我们通过重写先序遍历和后序遍历的钩子定义了一个子类。新的实现如代码段 8-31 所示。
class ParenthesizeTour(EulerTour):
def _hook_previsit(self, p, d, path):
if path and path[-1] > 0: # p follows a sibling
print(', ', end='') # so preface with comma
print(p.element(), end='') # then print element
if not self.tree().is_leaf(p): # if p has children
print(' (', end='') # print opening parenthesis
def _hook_postvisit(self, p, d, path, results):
if not self.tree().is_leaf(p): # if p has children
print(')', end='') # print closing parenthesis
注意,在这个实现中,我们在树的实例中调用一个从内部钩子遍历的方法。欧拉遍历类的公共 tree()方法作为树的访问器。
最后,计算磁盘空间的任务(如代码段 8-26 所示)可以用代码段 8-32 所示的 EulerTour 子类很容易地实现。根的后序遍历通过调用 execute() 返回结果。
class DiskSpaceTour(EulerTour):
def _hook_postvisit(self, p, d, path, results):
# we simply add space associated with p to that of its subtrees
return p.element().space() + sum(results)
二叉树的欧拉遍历¶
在 8.4.6 节中,我们介绍了一般图的欧拉遍历的概念,使用模板方法模式设计 EulerTour 类。类提供的_hook_previsit 和 _hook_postvisit 方法可以被重载来定制遍历。代码段 8-33 给出了一个 BinaryEulerTour 特性,包括额外的_hook_invisit 方法——被每个位置调用一次, 在遍历左子树之后、右子树之前调用。
BinaryEulerTour 的实现代替了原来的_tour , 仅限于一个节点至多有两个孩子的情况。如果一个节点只有一个孩子,遍历将区分是左孩子还是右孩子。访问发生在一个左孩子访问之后,且在一个右孩子访问之前。在一片叶子的情况下,会连续调用三个钩子。
class BinaryEulerTour(EulerTour):
"""Abstract base class for performing Euler tour of a binary tree.
This version includes an additional _hook_invisit that is called after the tour
of the left subtree (if any), yet before the tour of the right subtree (if any).
Note: Right child is always assigned index 1 in path, even if no left sibling.
"""
def _tour(self, p, d, path):
results = [None, None] # will update with results of recursions
self._hook_previsit(p, d, path) # "pre visit" for p
if self._tree.left(p) is not None: # consider left child
path.append(0)
results[0] = self._tour(self._tree.left(p), d+1, path)
path.pop()
self._hook_invisit(p, d, path) # "in visit" for p
if self._tree.right(p) is not None: # consider right child
path.append(1)
results[1] = self._tour(self._tree.right(p), d+1, path)
path.pop()
answer = self._hook_postvisit(p, d, path, results) # "post visit" p
return answer
def _hook_invisit(self, p, d, path):
"""Visit Position p, between tour of its left and right subtrees."""
pass
为了演示 BinaryEulerTour 的框架,我们开发了一个用于计算二叉树的图形布局的子类,如图 8-22 所示。这个几何图形由一个算法确定,该算法用以下两条规则为二叉树 T 的每个位置 p 指定 x 坐标和 y 坐标。
- x(p) 是在 p 之前的 T 中遍历中访问的位置数量。
- y(p) 是 T 中 p 的深度
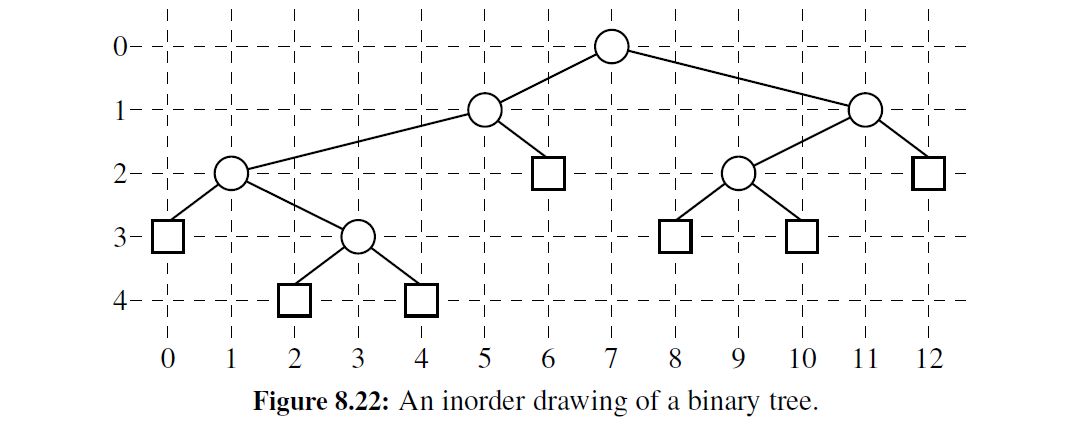
在这个应用中,我们采用计算机图形学中的一个公认约定,即 x 坐标从左到右增加, y 坐标从上到下增加,所以原点在计算机屏幕的左上角。
代码段 8-34 给出了一个 BinaryLayout 子类的实现,用于前面的算法,即实现为存储在二叉树每个位置的元素分配 (x, y) 坐标。我们以_count 实例变量(表示我们已执行“invisits" 的数量)的形式引入额外的状态,从而调整 BinaryEulerTour 框架。每个位置的 x 坐 标根据计数器设置。
class BinaryLayout(BinaryEulerTour):
"""Class for computing (x,y) coordinates for each node of a binary tree."""
def __init__(self, tree):
super().__init__(tree) # must call the parent constructor
self._count = 0 # initialize count of processed nodes
def _hook_invisit(self, p, d, path):
p.element().setX(self._count) # x-coordinate serialized by count
p.element().setY(d) # y-coordinate is depth
self._count += 1 # advance count of processed nodes
8.5 案例研究:表达式树¶
在例 8-7 中,我们介绍了使用二叉树来表示算数表达式的结构。在本节中,我们定义一个新类 ExpressionTree 为构建树提供支持,显示和评估树呈现的算术表达式。ExpressionTree 类被定义为 LinkedBinaryTree 类的子类。我们用非公开调整器来构建这样的树。每个内部节点必须存储一个用于定义二进制操作(如+)的字符串,每片叶子必须存储一个数值(或者一个字符串代表一个数值) 。
最终目的是将任意复杂度的表达式树建立为复合运算表达式,如 (((3 + 1) X 4)/((9 - 5) + 2)) 。然而,它仅支持两种基本形式来初始化表达式树类。
ExpressionTree(value):创建一棵在根处存储给定值的树。ExpressionTree(op, E1, E2):创建一棵在根处存储字符串 op (如+)的树, ExpressionTree 的实例 \(E_1\) 和 \(E_2\) 分别作为根的左子树和右子树。
ExpressionTree 的构造函数在代码段 8-35 中给出,该类正式继承自 LinkedBinaryTree, 所以它访问 8-35 节中定义的非公开更新方法。我们使用_add_root 方法来创建树的初始根,用以将令牌作为第一个参数存储,然后执行运行时参数来检查调用者是调用构造函数的单个参数版本(在这种情况下,我们已经做完了)还是 3 个参数形式。在这种情况下,我们结合树的结构使用继承的_attach 方法作为根的子树
组成一个括号字符串表示¶
现有表达式树实例的字符串表示,例如 (((3 + 1) X 4)/((9 - 5) + 2)),可以通过中序遍历树的方法来产生,但左括号和右括号分别用先序和后序步骤插入。ExpressionTree 类的上下文中,我们支持一个特殊的 __str__方法(见 2.3.2 节)返回一个合适的字符串。因为它更 高效地先将一系列独立的字符串连接在一起(见 5.4.2 节中 ” 组合字符串"的讨论), str 的实现依赖于一个非公开、递归的方法_parenthesize_recur, 该方法用于在一个列表中添加一系列字符串。这些方法被包含在代码段 8-35 中。
from .linked_binary_tree import LinkedBinaryTree
class ExpressionTree(LinkedBinaryTree):
"""An arithmetic expression tree."""
def __init__(self, token, left=None, right=None):
"""Create an expression tree.
In a single parameter form, token should be a leaf value (e.g., '42'),
and the expression tree will have that value at an isolated node.
In a three-parameter version, token should be an operator,
and left and right should be existing ExpressionTree instances
that become the operands for the binary operator.
"""
super().__init__() # LinkedBinaryTree initialization
if not isinstance(token, str):
raise TypeError('Token must be a string')
self._add_root(token) # use inherited, nonpublic method
if left is not None: # presumably three-parameter form
if token not in '+-*x/':
raise ValueError('token must be valid operator')
self._attach(self.root(), left, right) # use inherited, nonpublic method
def __str__(self):
"""Return string representation of the expression."""
pieces = [] # sequence of piecewise strings to compose
self._parenthesize_recur(self.root(), pieces)
return ''.join(pieces)
def _parenthesize_recur(self, p, result):
"""Append piecewise representation of p's subtree to resulting list."""
if self.is_leaf(p):
result.append(str(p.element())) # leaf value as a string
else:
result.append('(') # opening parenthesis
self._parenthesize_recur(self.left(p), result) # left subtree
result.append(p.element()) # operator
self._parenthesize_recur(self.right(p), result) # right subtree
result.append(')') # closing parenthesis
表达式树的评计算¶
表达式树的数值计算可以用先序遍历的简单应用完成。如果知道两个子树内部节点的位置, 我们可以计算指定位置的计算结果。代码段 8-36 给出了根在 p 位置处子树的计算值的递归伪代码。
Algorithm evaluate recur(p):
if p is a leaf then
return the value stored at p
else
let ◦ be the operator stored at p
x = evaluate recur(left(p))
y = evaluate recur(right(p))
return x ◦ y
为了用 python 的 ExpressionTree 类实现这个算法,我们提供了一个公共的 evaluate 方 法,它用 T.evaluate() 调用实例 T 。代码段 8-37 给出了这样一个实现——用一个非公开计算方法 _evaluate_recur 计算指定子树的值。
def evaluate(self):
"""Return the numeric result of the expression."""
return self._evaluate_recur(self.root())
def _evaluate_recur(self, p):
"""Return the numeric result of subtree rooted at p."""
if self.is_leaf(p):
return float(p.element()) # we assume element is numeric
else:
op = p.element()
left_val = self._evaluate_recur(self.left(p))
right_val = self._evaluate_recur(self.right(p))
if op == '+':
return left_val + right_val
elif op == '-':
return left_val - right_val
elif op == '/':
return left_val / right_val
else: # treat 'x' or '*' as multiplication
return left_val * right_val
创建一棵表达式树¶
代码段 8-35 中 ExpressionTree 的构造函数, 提供了结合现有树构建更大表达式树的基 本功能。然而,对于给定的字符串,如(((3 + }) X 4)/((9 - 5) + 2)) ,如何构建一棵表示该表达式的树,这一问题尚未解决。
为了将这个过程自动化,我们使用一个自上而下的构造算法,假设一个字符串可以先被标记化,这样多位数字就可以自动处理(见练习 R-8.30 ) ,从而这个表达式就完全被括起来了。算法使用栈 S 扫描输入表达式 E 来查找值、操作符和右括号(左括号被忽略) 。
- 当看到一个操作 \(\circ\) 时,我们将字符串推入栈。
- 当看到一个文本值 v 时,我们创建一个单个节点表达式树 T 存储 v, 并将 T 推入栈中。
- 当看到一个右括号 ”)” 时,我们从栈 S 的最顶端抛出三个元素,它代表子表达式 (\(E_1\circ E_2\)) 。我们构造树 T, 使用根的子树存储 \(E_1\) 和 \(E_2\) ,并把结果树 T 放回栈中
我们重复这个过程直到表达式 E 被处理完,每一次栈顶元素都是表达式树 E。总共的运行时间为 O(n) 。算法的实现在代码段 8-38 中以独立函数 build_expression_ tree 的形式给出,该函数返回 一个适当的 ExpressionTree 实例,假设输入已经被标记化。
def tokenize(raw):
"""Produces list of tokens indicated by a raw expression string.
For example the string '(43-(3*10))' results in the list
['(', '43', '-', '(', '3', '*', '10', ')', ')']
"""
SYMBOLS = set('+-x*/() ') # allow for '*' or 'x' for multiplication
mark = 0
tokens = []
n = len(raw)
for j in range(n):
if raw[j] in SYMBOLS:
if mark != j:
tokens.append(raw[mark:j]) # complete preceding token
if raw[j] != ' ':
tokens.append(raw[j]) # include this token
mark = j+1 # update mark to being at next index
if mark != n:
tokens.append(raw[mark:n]) # complete preceding token
return tokens
def build_expression_tree(tokens):
"""Returns an ExpressionTree based upon by a tokenized expression.
tokens must be an iterable of strings representing a fully parenthesized
binary expression, such as ['(', '43', '-', '(', '3', '*', '10', ')', ')']
"""
S = [] # we use python list as stack
for t in tokens:
if t in '+-x*/': # t is an operator symbol
S.append(t) # push the operator symbol
elif t not in '()': # consider t to be a literal
S.append(ExpressionTree(t)) # push trivial tree storing value
elif t == ')': # compose a new tree from three constituent parts
right = S.pop() # right subtree as per LIFO
op = S.pop() # operator symbol
left = S.pop() # left subtree
S.append(ExpressionTree(op, left, right)) # repush tree
# we ignore a left parenthesis
return S.pop()
if __name__ == '__main__':
big = build_expression_tree(tokenize('((((3+1)x3)/((9-5)+2))-((3x(7-4))+6))'))
print(big, '=', big.evaluate())