第 9 章 优先级队列

9.1 优先级队列的抽象数据类型

9.1.1 优先级

在第 6 章，我们介绍了队列 ADT 是一个根据先进先出( FIFO ) 策略在队列中添加和移除数据的对象集合。公司的客户呼叫中心实现了这样一个模型： 在该模型中，客户被告知 ” 呼叫将按照呼叫中心接受的顺序来应答＂ 。在其设置中， 一个新的呼叫被追加到队列的末尾，每当一个客户服务代表可以提供服务时，他将应答等待队列最前端的客户。

在现实生活中，有许多应用使用类似队列的结构来管理需要顺序处理的对象， 但仅有先进先出的策略是不够的。比如，假设一个空中交通管制中心必须决定在众多即将降落的航班中先为哪次航班清理跑道。这个选择可能受到各种因素的影响，比如每个飞机跑道之间的距离、着陆过程中所用的时间或燃料的余量。着陆决定纯粹基于一个 FIFO 策略是不太可能的。

“先来先服务” 策略在某些情况下是合理的，但在另一些情况下，优先级才是起决定作用的。现在，我们用另一个航空公司的例子加以说明，假设一个航班在起飞前一个小时被订满，由于有旅客取消的可能，航空公司维护了一个希望获得座位的候补等待 (standby) 旅客的队列。尽管等待旅客的优先级受到其检票时间的影响，但包括支付机票和是否频繁飞行 （常飞乘客）在内的其他因素都需要考虑。因此，如果某位乘客被航空公司代理赋予了更高的优先级，那么当飞机上出现空闲座位时，即使他比其他乘客到得晚，他也有可能买到这张 机票。

在本章中，我们介绍一个新的抽象数据类型，那就是优先级队列。这是一个包含优先级元素的集合，这个集合允许插入任意的元素，并允许删除拥有最高优先级的元素。当一个元素被插入优先级队列中时，用户可以通过提供一个关联键来为该元素赋予一定的优先级。键值最小的元素将是下一个从队列中移除的元素（因此， 一个键值为 1 的元素将获得比键值为 2 的元素更高的优先级） 。虽然用数字表示优先级是相当普遍的，但是任何 python 对象，只要对象类型中的任何实例 a 和 b , 对于 a < b 都支持一个一致的释义， 那么该对象就可以用 于定义键的自然顺序。有了这样的普遍性，应用程序可以为每个元素定义它们自己的优先级概念。比如，不同的金融分析师可以给特定的资产指定不同的评级（即优先级），如股票的份额。

9.1.2 优先级队列的抽象数据类型的实现

我们形式化地将一个元素和它的优先级用一个 key-value 对进行建模。我们在优先级队列 P 上定义优先级队列 ADT , 以支持如下的方法：

• P.add(k, v) ：向优先级队列 P 中插入一个拥有键 k 和值 v 的元组。
• P.min()：返回一个元组 (k,v)，代表优先级队列 P 中一个包含键和值的元组，该元组的键值是最小值（但是没有移除该元组）；如果队列为空，将发生错误。
• P.remove_min()：从优先级队列 P 中移除一个拥有最小键值的元组，并且返回这个被移除的元组，（ k,v ) 代表这个被移除的元组的键和值；如果优先级队列为空，将发生错误。
• P.is_empty()：如果优先级队列不包含任何元组，将返回 True 。
• len(P) ：返回优先级队列中元组的数量。

一个优先级队列中可能包含多个键值相等的条目，在这种情况下 min 和 remove_min 方法可能从具有最小键值的元组中任选一个返回。值可以是任何对象类型。

在优先级队列的初始模型中，假设一个元素一旦被加入优先级队列，它的键值将保持不变。在 9.5 节中，我们考虑对这个初始模型进行扩展，扩展后允许用户更新优先级队列中的元素的键。

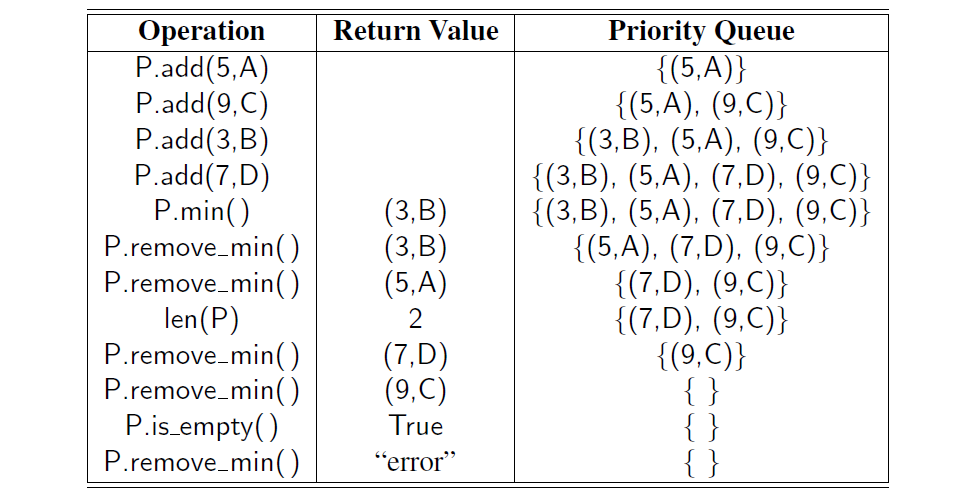
例题 9-1 :下表展示了一个初始为空的优先级队列 P 中的一系列操作及其产生的效果。由于它将条目以键排序的元组形式列出，因此 “优先级队列”一列是有误的。这样的一个内部表示不需要优先级队列

9.2 优先级队列的实现

在本节中，我们将展示如何通过给一个位置列表 L 中的条目排序来实现一个优先级队列 （见 7.4 节） 。根据在列表 L 中保存条目时是否按键排序，我们提供了两种实现

9.2.1 组合设计模式

即使在数据结构中巳经重新定义了元组，我们仍需要同时追踪元素和它的键值，这是实现优先级队列的挑战之一。这一点让我们想起在 7.6 节的案例讨论中，我们为每个元素维护一个访问计数器的做法。在那种设定下，我们介绍了组合设计模式，定义了一个 _Item 类， 用它来确保在主要的数据结构中每个元组保存它相关计数值。

对于优先级队列，我们将使用组合设计模式来存储内部元组，该元组包含键 k 和值 v 构 成的数值对。为了在所有优先级队列中实现这种概念，我们给出了一个 PriorityQueueBase 类（见代码段 9-1)，其中包含一个嵌套类＿Item 的定义。对于元组实例 a 和 b, 我们基于关键字定义了语法 a < b 。

from ..exceptions import Empty

class PriorityQueueBase:
  """Abstract base class for a priority queue."""

  #------------------------------ nested _Item class ------------------------------
  class _Item:
    """Lightweight composite to store priority queue items."""
    __slots__ = '_key', '_value'

    def __init__(self, k, v):
      self._key = k
      self._value = v

    def __lt__(self, other):
      return self._key < other._key    # compare items based on their keys

    def __repr__(self):
      return '({0},{1})'.format(self._key, self._value)

  #------------------------------ public behaviors ------------------------------
  def is_empty(self):                  # concrete method assuming abstract len
    """Return True if the priority queue is empty."""
    return len(self) == 0

format 的作用

9.2.2 使用未排序列表实现优先级队列

在第一个具体的优先级队列实现中，我们使用一个未排序列表存储各个条目。代码段 9-2 中 给出了 UnsortedPriorityQueue 类，它继承自代码段 9-1 中的 PriorityQueueBase 类。对于内部存储，键－值对是使用继承类＿Item 的实例进行组合表示的。这些元组是用 PositionalList 存储的，它们被视为类中的＿data 成员。在 7.4 节中，我们假设位置列表用一个双向链表实现，因此所有 ADT 操作执行的时间复杂度为 O(1) 。

在构建一个新的优先级队列时，我们从一个空的列表开始。无论何时，列表的大小都等于存储在优先级队列中键－值对的数量。由于这个原因，优先级队列 __len__ 方法能够简单地返回内部＿data 列表的长度。通过设计我们的 PriorityQueueBase 类，可以继承 is_empty 方法的具体实现，这种方法依赖于调用我们的__len__方法。

通过 add 方法，每次将一个键－值对追加到优先级队列中，对于给定的键和值，我们创建了一个新的＿Item 的元组（组成），并且将这个元组追加到列表的末端。这一实现的时间复杂度为 O(1) 。

当 min 或者 remove_min 方法被调用时，我们必须定位键值最小的元组，这是另一个挑战。由于元组没有被排序，我们必须检查所有元组才能找到键值最小的元组。为了方便， 我们定义了一个非公有的方法 _find_min, 它用于返回键值最小的元组的位置。获得了位置信息，就允许 remove_min 方法可以在位置列表上调用 delete 方法。当准备返回一个键－ 值对元组时， min 方法可以简单地使用位置来检索列表元组。由于是用循环查找最小键值的，因此 min 和 remove_min 方法的时间复杂度均为 O(n) ， 其中 n 为优先级队列中元组的数量。

对于 UnsortedPriorityQueue 类的时间复杂度的总结见表 9-1

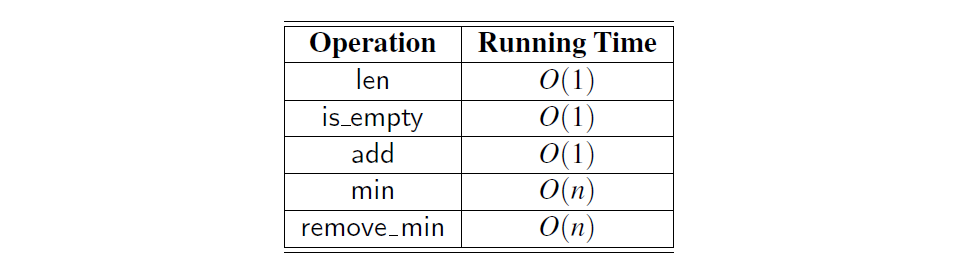
表 9.1：大小为 n 的优先级队列方法的最坏情况运行时间，通过未排序的双向链表实现。 空间要求为 O(n)。

from .priority_queue_base import PriorityQueueBase
from ..ch07.positional_list import PositionalList
from ..exceptions import Empty

class UnsortedPriorityQueue(PriorityQueueBase): # base class defines _Item
  """A min-oriented priority queue implemented with an unsorted list."""

  #----------------------------- nonpublic behavior -----------------------------
  def _find_min(self):
    """Return Position of item with minimum key."""
    if self.is_empty():               # is_empty inherited from base class
      raise Empty('Priority queue is empty')
    small = self._data.first()
    walk = self._data.after(small)
    while walk is not None:
      if walk.element() < small.element():
        small = walk
      walk = self._data.after(walk)
    return small

  #------------------------------ public behaviors ------------------------------
  def __init__(self):
    """Create a new empty Priority Queue."""
    self._data = PositionalList()

  def __len__(self):
    """Return the number of items in the priority queue."""
    return len(self._data)

  def add(self, key, value):
    """Add a key-value pair."""
    self._data.add_last(self._Item(key, value))

  def min(self):
    """Return but do not remove (k,v) tuple with minimum key.

    Raise Empty exception if empty.
    """
    p = self._find_min()
    item = p.element()
    return (item._key, item._value)

  def remove_min(self):
    """Remove and return (k,v) tuple with minimum key.

    Raise Empty exception if empty.
    """
    p = self._find_min()
    item = self._data.delete(p)
    return (item._key, item._value)

9.2.3 使用排序列表实现优先级队列

优先级队列的另一个替代实现是使用位置列表，列表中的元组以键值非递减的顺序进行排序。这样可以保证列表的第一个元组是拥有最小键值的元组。

代码段 9-3 给出了 SortedPriorityQueue 类。方法 min 和 remove_min 的实现相当直接地给出了列表的第一个元素拥有最小键值的信息。我们根据位置列表的 first 方法来找到第一个元组的位置，并使用 delete 方法来删除列表中的元组。假设列表是使用一个双向链表实现 的，那么 min 和 remove_min 操作的时间复杂度为 O( 1 ) 。

然而，这个好处是以 add 方法花费更多的时间成本为代价的，我们需要扫描列表来找到合适的位置，以插入新的元组。实现从列表的结尾开始反方向查找，直到新的键值比当前元组的键值小为止；在最坏情况下，这个操作会一直扫描到列表的最前端。因此， add 方法在 最坏情况下的时间复杂度是 O(n), n 是执行该方法时优先级队列元组的数量。总之， 当使用 一个已排序列表来实现优先级队列时，插入操作的运行时间是线性的，而查找和移除最小键值的元组的操作则能在常数时间内完成

比较两种基于列表的实现

表 9-2 详细地比较了分别通过已排序列表和未排序列表实现的优先级队列的各方法的运行时间。当使用列表来实现优先级队列 ADT 时，我们看到一个有趣的权衡。一个未排序的列表会支持快速插入操作，但是查询和删除操作就会比较慢；相反，一个已排序列表实现的优先级队列支持快速查询和删除操作，但是插入操作就比较慢

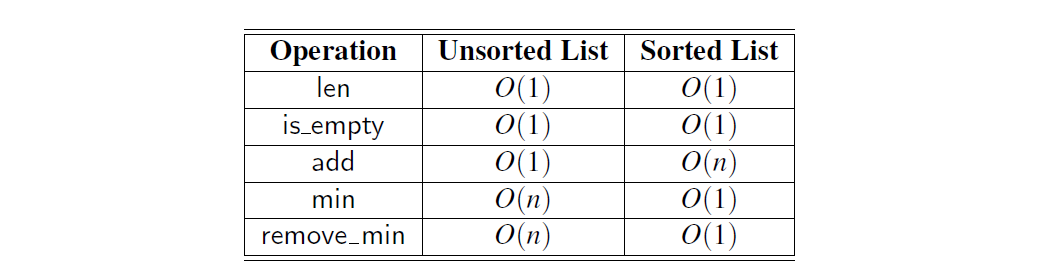
表 9.2：大小为 n 的优先级队列方法的最坏情况运行时间，分别通过未排序或排序列表实现。 我们假设列表是由双向链表实现的。 空间要求为 O(n)。

from .priority_queue_base import PriorityQueueBase
from ..ch07.positional_list import PositionalList
from ..exceptions import Empty

class SortedPriorityQueue(PriorityQueueBase): # base class defines _Item
  """A min-oriented priority queue implemented with a sorted list."""

  #------------------------------ public behaviors ------------------------------
  def __init__(self):
    """Create a new empty Priority Queue."""
    self._data = PositionalList()

  def __len__(self):
    """Return the number of items in the priority queue."""
    return len(self._data)

  def add(self, key, value):
    """Add a key-value pair."""
    newest = self._Item(key, value)             # make new item instance
    walk = self._data.last()       # walk backward looking for smaller key
    while walk is not None and newest < walk.element():
      walk = self._data.before(walk)
    if walk is None:
      self._data.add_first(newest)              # new key is smallest
    else:
      self._data.add_after(walk, newest)        # newest goes after walk

  def min(self):
    """Return but do not remove (k,v) tuple with minimum key.

    Raise Empty exception if empty.
    """
    if self.is_empty():
      raise Empty('Priority queue is empty.')
    p = self._data.first()
    item = p.element()
    return (item._key, item._value)

  def remove_min(self):
    """Remove and return (k,v) tuple with minimum key.

    Raise Empty exception if empty.
    """
    if self.is_empty():
      raise Empty('Priority queue is empty.')
    item = self._data.delete(self._data.first())
    return (item._key, item._value)

9.3 堆

在前面的两节中， 实现优先级队列 ADT 的两种策略展示了一个有趣的权衡。当使用一个未排序列表来存储元组时，我们能够以 O(1) 的时间复杂度实现插入，但是查找或者移除一个具有最小键值的元组则需要时间复杂度为 O (n) 的循环操作来遍历整个元组集合。相对应地，如果使用一个已排序列表实现的优先级队列，则可以以 O(1) 的时间复杂度查找或者移除具有最小键值的元组，但是向队列追加一个新的元素就需要 O(n) 的时间来重新存储这个排序列表的序列。

在本节中，我们使用一个称为二进制堆的数据结构来给出一个更加有效的优先级队列的实现。这个数据结构允许我们以对数时间复杂度来实现插入和删除操作，这相对于 9.2 节讨论的基于列表的实现有很大的改善。利用堆实现这种改善的基本方式是使用二叉树的数据结构来在元素是完全无序和完全排好序之间取得折中。

9.3.1 堆的数据结构

堆（见图 9-1 ) 是一棵二叉树 T, 该树在它的位置（节点） 上存储了集合中的元组并且满足两个附加的属性： 关系属性以存储键的形式在 T 中定义；结构属性以树 T 自身形状的方式 定义。关系属性如下：

• Heap - Order 属性：在堆 T 中，对于除了根的每个位置 p, 存储在 p 中的键值大于或等于存储在 p 的父节点的键值。

作为 Heap-Order 属性的结果， T 中从根到叶子的路径上的键值是以非递减顺序排列的。

也就是说， 一个最小的键总是存储在 T 的根节点中。这使得调用 min 或 remove_min 时，能够比较容易地定位这样的元组，一般情况下它被认为 “在堆的顶部”（因此，给这种数据 结构命名为＂堆＂） 。顺便说一下，这里定义的数据结构堆与被用作支待一种程序语言（如 python ) 的运行环境的内存堆（见 15.1.1 节）没并无任何关系。

由于效率的缘故，我们想让堆 T 的高度尽可能小，原因后面就会清楚。我们通过坚持让堆 T 满足结构属性中的附加属性，来强制满足让堆的高度尽可能小这一需求——它必须是完全二叉树。

• 完全二叉树属性：一个高度为 h 的堆 T 是一棵完全二叉树，那么 T 的 0,1, 2, …,h - 1 层上有可能达到节点数的最大值（即，\(i\) 层上有 \(2^i\) 个节点，且 \(0\le i\le h-1\))，并且剩余的节点在 h 级尽可能保存在最左的位置。

图 9-1 中的树是完全二叉树，因为树的 0 、1 、2 层都是满的，并且 3 层的 6 个节点都处在该层的最左边位置上。对于最左边位置的正式说法，我们可以参考 8.3.2 节中有关层级编号的讨论，即基于数组的二叉树表示的相关内容（事实上，在 9.3.3 节中，我们将会讨论使用数组来表示堆） 。一棵含有 n 个节点的完全二叉树，是一棵含有从 0 到 n -1 层级编号的位置的树。比如， 在一个基于数组的完全二叉树的表示中，它的 13 个元组将被连续地存储在 A[0] 到 A[12] 中。

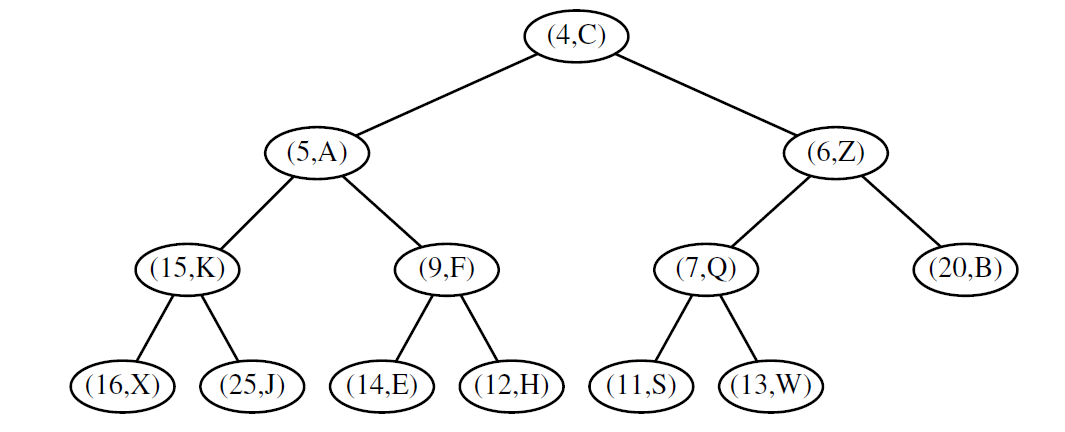
图 9.1：存储 13 个具有整数键的条目的堆示例。 最后一个位置是一个存储条目 (13,W)。

堆的高度

使用 h 表示 T 的高度。T 为完全二叉树一定会有一个重要的结论， 如命题 9-2 所示

命题 9-2: 堆 T 有 n 个元组，则它的高度 \(h =\left\lfloor\log n\right\rfloor\)。

证明： 由 T 是完全二叉树可知，完全二叉树 \(T\ 0 \sim h - 1\) 层节点的数量是 \(1+2+4+ …+ 2^{h-1}= 2^h- 1\) ，并且在 h 层的节点数最少为 1 个最多为 \(2^h\) 个。因此可得：

\[ n \le 2^h - 1 + 1 = 2^h\ 和\ n \le 2^h - 1 + ^2h = 2^{h+1} - 1 \]

给不等式 \(2^h \le n\) 两边取对数，得到高度 \(h \le \log n\) 。给不等式 \(n \le 2^{h+1} - 1\) 两边取对数，得到 \(\log(n+ 1)- 1\le h\) 。由于 h 为整数，因此这两个不等式可简化为 \(h =\left\lfloor\log n\right\rfloor\)

9.3.2 使用堆实现优先级队列

命题 9-2 有一个重要的结论，那就是如果能以与堆的高度成比例的时间执行更新操作， 那么这些操作将在对数级的时间内完成。现在，我们来讨论如何有效地使用堆来实现优先级队列中的各个方法。

我们将使用 9.2.1 节的组合模式来在堆中存储键－值对的元组。len 和 is_empty 方法能够基于对树的检测来实现。min 操作相当简单，因为堆的属性保证了树的根部元组有最小的键值。add 和 remove_min 的实现方法都是有趣的算法。

在堆中增加一个元组

让我们考虑如何在一个用堆 T 实现的优先级队列上实现 add(k, v) 方法。我们把键值对 (k, v) 作为元组存储在树的新节点中。为了维持完全二叉树属性，这个新节点应该被放在位置 p 上，即树底层最右节点相邻的位置。如果树的底层节点已满（或堆为空）， 则应存放在新一层的最左位置上。

插入元组后堆向上冒泡

在这个操作之后，树 T 为完全二叉树，但是它可能破坏了 heap-order 属性。因此，除非位置 p 是树 T 的根节点（也就是说，优先级队列在插入操作前是空的），否则我们将对 p 位置上的键值与 p 的父节点 q （定义 p 的父节点为 q) 上的键值进行比较。如果 \(k_p \ge k_q\), 则满足 heap-order 属性且算法终止。如果 \(k_p < k_q\), 则需要重新调整树以满足 heap-order 属性，我们通过调换存储在位置 p 和 q 的元组来实现（ 见图 9-2c 和图 9-2d ) 。这个交换导致新元组的层次上移一层。而 heap-order 属性可能再次被破坏，因此，我们需要在树 T 重复以上操作， 直到不再违背 heap-order 属性位置（ 见图 9-2 中的 e 和图 9-2h) 。

通过交换方式上移新插入的元组是非常方便的，这种操作被称作堆向上冒泡( up-heap bubbling ) 。交换既解决了破坏 heap-order 属性的问题，又将元组在堆中向上移一层。在最坏情况下， 堆向上冒泡会导致新增元组向上一直移动到堆 T 的根节点位置。所以， add 方法所执行的交换次数在最坏情况下等于 T 的高度。根据命题 9-2 , 我们得知高度的上界是 \(\left\lfloor\log n\right\rfloor\)。

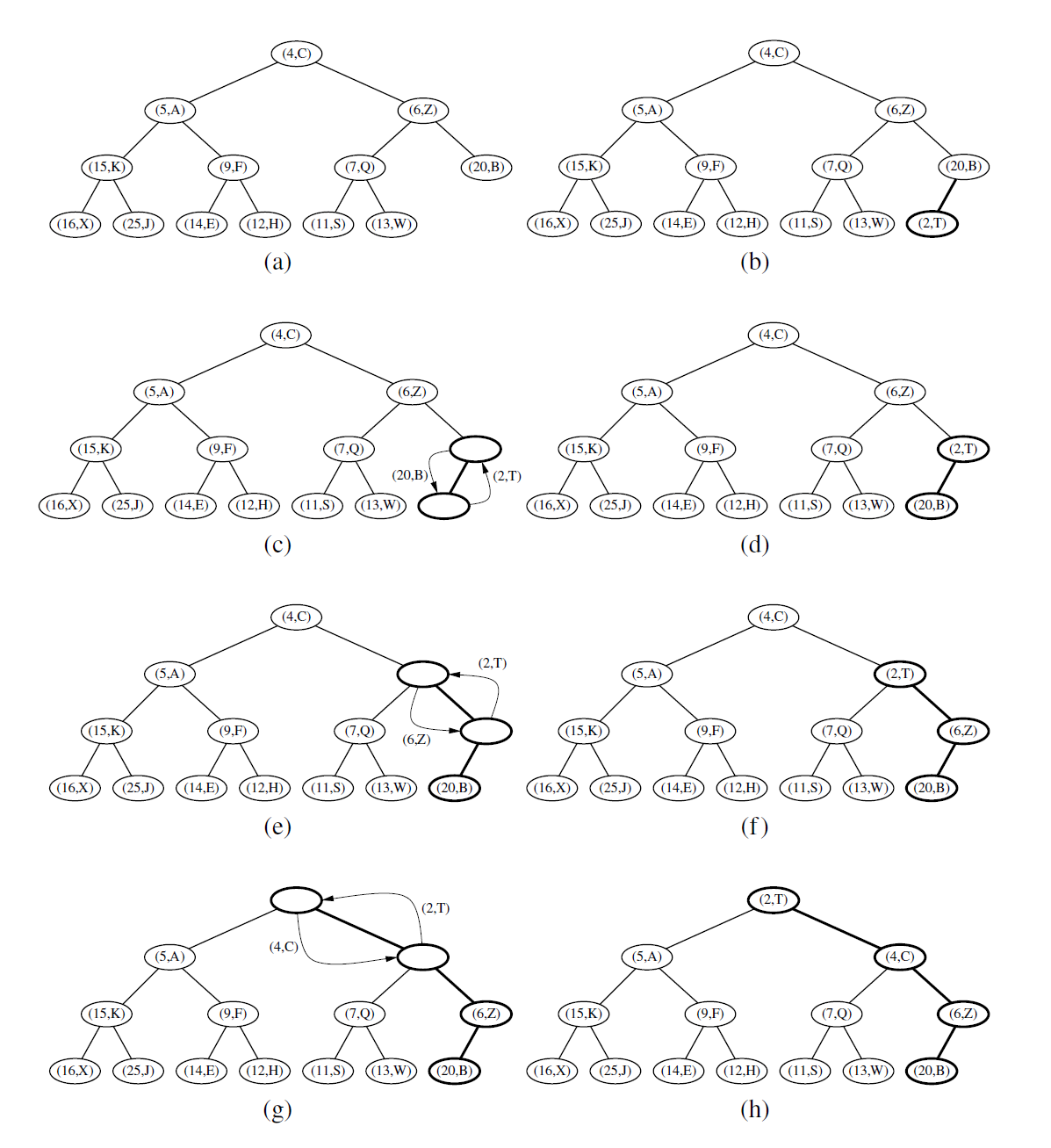
图 9.2：将带有键 2 的新条目插入到图 9.1 的堆中：(a) 初始堆； (b) 在执行添加操作之后； (c 和 d) 交换以在本地恢复偏序属性； (e 和 f) 另一个交换； （g 和 h）最终交换。

移除键值最小的元组

让我们现在考虑优先级队列 ADT 的 remove_min方法。我们知道键值最小的元组被存储在堆 T 的根节点 r 上（即使有多于一个元组含有最小键值）。但是， 一般情况下我们不能简单删除节点 r, 因为这将产生两棵不相连通的子树。

相反，我们可以通过删除堆 T 最后位置 p 上的叶子节点来确保堆的形状满足完全二叉树属性，这个最后位置 p 是树最底层的最靠右的位置。为了保存最后位置 p 上的元组，我们将该位置上的元组复制到根节点 r （就是那个即将要执行删除操作的含有最小键值的元组） 。图 9-3a 和图 9-3 b 展示了有关这些步骤的一个例子，含最小键值的元组 ( 4, C ) 被从根部删 除之后，该位置由来自最后位置的元组 ( 13 , W ) 所填充。在最后位置的节点被从树中删除。

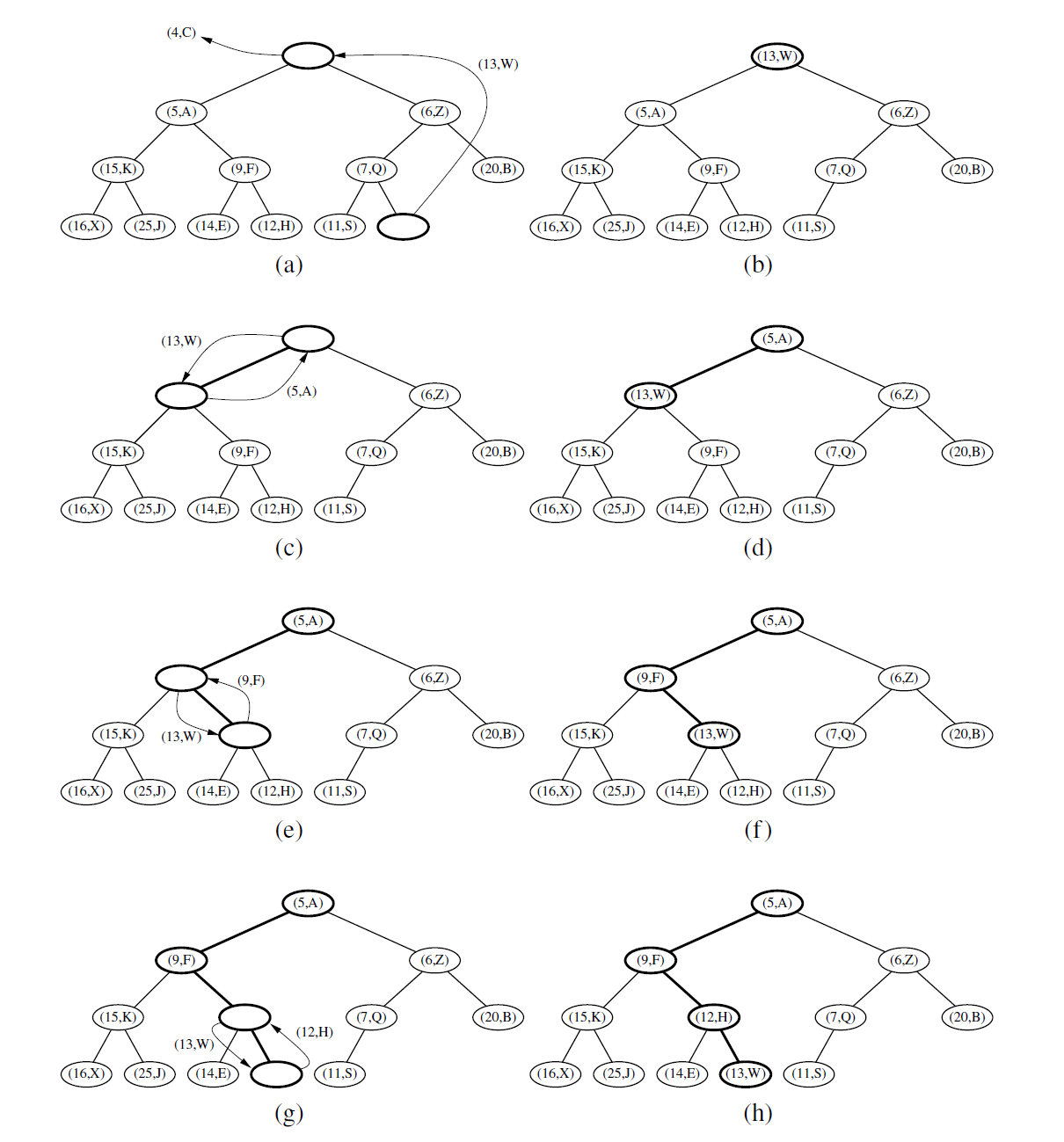
图 9.3：从堆中删除具有最小键的条目：（a 和 b）删除最后一个节点，其条目存储在根中； (c 和 d) 交换以在本地恢复堆顺序属性； (e 和 f) 另一个交换； （g 和 h）最终交换。

删除操作后堆向下冒泡

在还没有做任何处理时，即使 T 现在是完全二叉树，它也很有可能已经破坏了 heap-order 属性。如果 T 只有一个节点（根），那么 heap-order 属性可以很简单地满足且算法终止。否则，我们需要区分两种清况，这里将 p 初始化为 T 的根：

1. 如果 p 没有右孩子，令 c 表示 p 的左孩子。
2. 否则( p 有两个孩子），令 c 作为 p 的具有较小键值的孩子。

如果 \(k_p \le k_c\). ，则 heap-order 属性已经满足，算法终止；如果 \(k_p > k_c\) , 则需要重新调整元组位置来满足 heap-order 属性。我们可以通过交换存储在 p 和 c 上的元组来使得局部满足 heap-order 属性（见图 9-3 c 和图 9-3d ) 。值得注意的是，当 p 有两个孩子时，我们着重考虑两个孩子节点中较小的那个。不仅 c 的键值要比 p 的键值小，还要至少和 c 的兄弟节点的键值一样小。这样能够确保当较小的键值被提升到 p 或 c 的兄弟位置之上的位置时，我们能够通过局部调整的方式来满足 heap-order 属性。

在恢复了节点 p 相对于其孩子节点的 heap-order 属性后，节点 c 可能违反了该属性。因此，我们必须继续向下交换直到没有违反 heap-order 属性的情况发生（见图 9-3e ～ 图 9-3 h ) 。

这个向下交换的过程被称作堆向下冒泡( dowm-beap bubbling ) 。交换可以解决违反 heap-order 属性的问题或者导致该键值在堆中下移一层。在最坏情况下，元组会一直下移到堆的最底层（见图 9-3 ) 。这样，在最坏情况下，在执行方法 remove_min 中交换的次数等于堆 T 的高度，即根据命题 9-2 可知，这个最大值是 \(\left\lfloor\log n\right\rfloor\)。

9.3.3 基于数组的完全二叉树表示

基于数组的二叉树表示( 8.3.2 节）非常适合完全二叉树 T。在这部分实现中我们还使用它， T 的元组被存储在基于数组的列表 A 中，因此，存储在 T 中位置 p 的元素的索引等于层数 \(f(p)\), \(f(p)\) 是 p 的函数，其定义如下：

• 若 p 是 T 的根节点，则 \(f(p)＝0\) 。
• 若 p 是位置 q 的左孩子，则 \(f(p)＝2f(q) + 1\) 。
• 若 p 是位置 q 的右孩子，则 \(f(p)＝2f(q) + 2\) 。

通过这种实现， T 的元组有落在 \([ 0 , n - 1]\) 范围内相邻的索引， 而且 T 最后节点的总是在索引 n - 1 的位置上，其中 n 是 T 的元组数量。例如，图 9-1 基于数组表示的堆结构示意图如图 9-4 所示。

图 9.4：图 9.1 中堆的基于数组的表示。

用基于数组表示的堆来实现优先级队列使我们避免了基于节点树结构的一些复杂性。尤其是优先级队列的 add 和 remove_min 操作都依靠定位大小为 n 的堆的最后一个索引位置。

使用基于数组的表示，最后位置是数组中下标为 n - 1 的位置。通过链结构实现定位完全二叉树的最后位置需要付出更多的代价（见练习 C-9.34 ) 。如果事先不知道优先级队列的大小， 基于数组表示堆的使用就会引入偶尔动态重新设置数组大小的需要， 就像 python 列表一样。这样一个基于数组表示的节点数为 n 的完全二叉树的空间使用复杂度为 O(n) ，而且增加和删除元组的方法的时间边界也需要考虑摊销 (amortized) （见 5.3.1 节） 。

9.3.4 python 的堆实现

代码段 9-4 和代码段 9-5 提供了一个基于堆的优先级队列的 python 实现。我们使用基于数组的表示，保存了元组组合表示的 python 列表。虽然没有正式使用二叉树 ADT, 但是代码段 9-4 包含了非公有效用函数，该函数能够计算父节点或另一个孩子节点的层次编号。这样就可以使用父节点、左孩子和右孩子等树相关术语来描述剩下的算法。但是，相关变量是整数索引（不是＂位置 ” 对象） 。我们采用递归来实现 _upheap 和 _downheap 中的重复调用。

from .priority_queue_base import PriorityQueueBase
from ..exceptions import Empty

class HeapPriorityQueue(PriorityQueueBase): # base class defines _Item
  """A min-oriented priority queue implemented with a binary heap."""

  #------------------------------ nonpublic behaviors ------------------------------
  def _parent(self, j):
    return (j-1) // 2

  def _left(self, j):
    return 2*j + 1

  def _right(self, j):
    return 2*j + 2

  def _has_left(self, j):
    return self._left(j) < len(self._data)     # index beyond end of list?

  def _has_right(self, j):
    return self._right(j) < len(self._data)    # index beyond end of list?

  def _swap(self, i, j):
    """Swap the elements at indices i and j of array."""
    self._data[i], self._data[j] = self._data[j], self._data[i]

  def _upheap(self, j):
    parent = self._parent(j)
    if j > 0 and self._data[j] < self._data[parent]:
      self._swap(j, parent)
      self._upheap(parent)             # recur at position of parent

  def _downheap(self, j):
    if self._has_left(j):
      left = self._left(j)
      small_child = left               # although right may be smaller
      if self._has_right(j):
        right = self._right(j)
        if self._data[right] < self._data[left]:
          small_child = right
      if self._data[small_child] < self._data[j]:
        self._swap(j, small_child)
        self._downheap(small_child)    # recur at position of small child

  #------------------------------ public behaviors ------------------------------
  def __init__(self):
    """Create a new empty Priority Queue."""
    self._data = []

  def __len__(self):
    """Return the number of items in the priority queue."""
    return len(self._data)

  def add(self, key, value):
    """Add a key-value pair to the priority queue."""
    self._data.append(self._Item(key, value))
    self._upheap(len(self._data) - 1)            # upheap newly added position

  def min(self):
    """Return but do not remove (k,v) tuple with minimum key.

    Raise Empty exception if empty.
    """
    if self.is_empty():
      raise Empty('Priority queue is empty.')
    item = self._data[0]
    return (item._key, item._value)

  def remove_min(self):
    """Remove and return (k,v) tuple with minimum key.

    Raise Empty exception if empty.
    """
    if self.is_empty():
      raise Empty('Priority queue is empty.')
    self._swap(0, len(self._data) - 1)           # put minimum item at the end
    item = self._data.pop()                      # and remove it from the list;
    self._downheap(0)                            # then fix new root
    return (item._key, item._value)

9.3.5 基于堆的优先级队列的分析

表 9-3 显示了基于堆实现的优先级队列 ADT 各方法的运行时间， 其中，假设两个键的比较能够在时间复杂度 O(1) 内完成，而且堆 T 是基于数组表示的树或基于链表表示的树实现的。

简言之，每个优先级队列 ADT 方法能够在时间复杂度 O(1) 或 O(\(\log n\)) 内完成，其中 n 是执行方法时堆中元组的数量。这些方法的运行时间的分析是基于以下结论得出的：

• 堆 T 有 n 个节点，每个节点存储一个键－ 值对的引用。
• 由于堆 T 是完全二叉树，所有堆 T 的高度是 O(\(\log n\)) （命题 9-1) 。
• 由于树的根部包含最小元组，因此 min 操作运行的时间复杂度是 O(1) 。
• 如 add 和 remove_min 操作中所需要的，定位堆的最后一个位置的操作，在基于数组表示的堆上完成需要的时间复杂度为 O(1) ， 在基于链表树表示的堆上需要以 O(\(\log n\)) 的时间复杂度完成（见练习 C-9.34) 。
• 堆向上冒泡和堆向下冒泡执行交换的次数在最坏情况下等于 T 的高度

表 9.3：通过堆实现的优先级队列 P 的性能。 我们让 n 表示执行操作时优先级队列中的条目数。 空间要求为 O(n)。 由于偶尔调整动态数组的大小，对于基于数组的表示，操作 min 和 remove_min 的运行时间被摊销； 这些边界是链接树结构的最坏情况。

我们可以得出这样的结论： 无论堆使用链表结构还是数组结构实现，堆数据结构都是优先级队列 ADT 非常有效的实现方式。与基于未排序或已排序列表的实现不同，基于堆的实现在插入和移除操作中均能快速地获得运行结果。

9.3.6 自底向上构建堆

如果以一个初始为空的堆开始，在最坏情况下，连续 n 次调用 add 操作的时间复杂度为 O(\(n \log n\)) 。但是，如果所有存储在堆中的键—值对都事先给定，比如在堆排序算法的第一阶段， 可以选择运行的时间复杂度为 O(n) 的自下而上的方法构建堆（但是，堆排序仍然需要 O(\(n \log n)\) 的时间复杂度，因为在第二阶段我们仍然是重复地移除剩余元组中具有最小键值的一个） 。

在这一节，我们描述了自底向上地构建堆，并给出了一个实现方法，基于堆的优先队列的构造函数可以使用这个实现方法来构建堆。

为了使叙述简单，我们在描述这种自底向上的堆构建时，假设键数量为 n , 并且 n 为 整数， \(n = 2^{h + 1} - 1\) 。也就是说，堆是一个每层都满的完全二叉树，所以堆的高度满足 \(h = \log(n + 1) - 1\) 。以非递归的方法描述，自底向上构建堆包含以下 \(h + 1 = \log(n + 1)\) 个步骤。

1. 第一步（见图 9-5b) ，我们构建 ( n + 1 )/2 个基本堆，每个堆中仅存储一个元组。

2. 第二步（见图 9-5c ～ 图 9-5d) ，我们通过将基本堆成对连接起来并增加一个新元组来构建 (n + 1)/4 个堆，这种堆的每个堆中存储了 3 个元组。新增的元组放在根部，并且它很有可能不得不与堆中某一个孩子节点存储的元组进行交换以保持 heap-order 属性

3. 第三步（见图 9-5e ～图 9-5f) ，我们通过成对连接含 3 个元组的堆（该堆在上一步中构建），并且增加个新的元组，从而构建 (n + 1)/8 个堆，每个堆存储 7 个元组。新增的元组存储在根节点，但是它可能通过堆向下冒泡算法下移以保持堆的 heap-order 属性

……

1. 第 i 步， \(2\le i\le h\) ，我们通过成对连接存有(\(2^{i-1}-1\)) 个元组的堆（该堆是在前一步中构建的），并且在每个合并的堆上增加一个新的元组来构建 \((n + 1 )/2^i\) 个堆，每个堆存储 \(2^i- 1\) 个元组。新增元组被存储在根节点上，但是它很可能需要通过堆向下冒泡算法进行下 移以保持堆的 heap-order 属性

……

1. h + 1) 最后一步（见图 9-5g ～图 9-5h ) ，我们通过连接两个存储了 (n - 1)/2 个元组的堆 （该堆是在上一步中构建的），并且增加新一个的元组来构建最终的堆，该堆存储了所有 n 个 元组。新增的元组开始存储在根节点， 但是它可能需要通过堆向下冒泡的算法下移以保持堆的 heap-order 属性。

h = 3 时、自底向上的建堆过程如图 9-5 所示

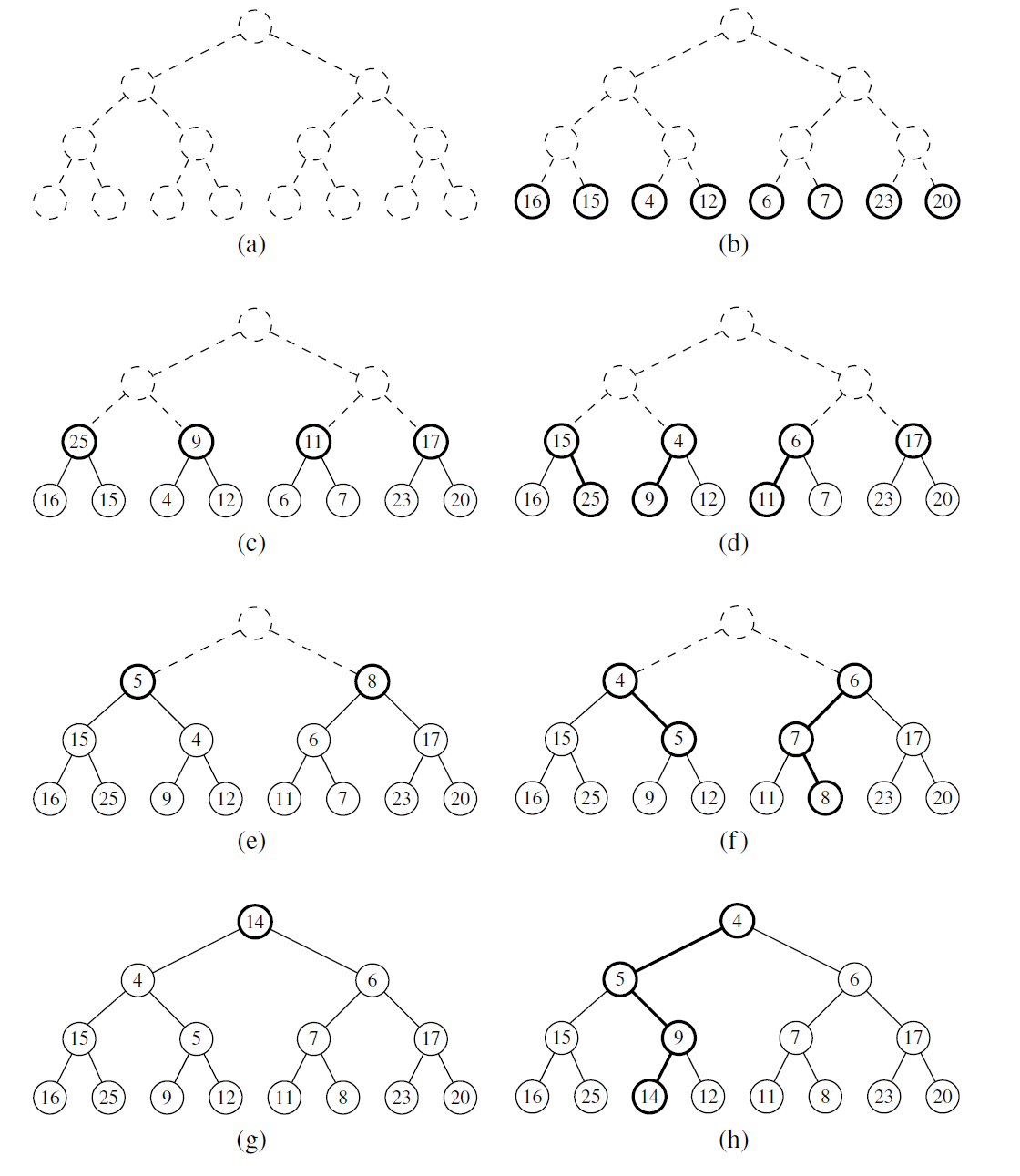
图 9.5：具有 15 个条目的堆的自下而上构造：（a 和 b）我们首先在底层构造 1 个条目的堆； (c 和 d) 我们将这些堆组合成 3 项堆，然后 (e 和 f ) 7 项堆，直到 (g 和 h) 我们创建最终堆。 下堆冒泡的路径在（d、f 和 h）中突出显示。 为简单起见，我们只显示每个节点中的键而不是整个条目。

自底向上构建堆的 python 实现

当给定了 “下堆” ( down-heap ) 效用函数( utility function ) 时， 实现自底向上构建堆非常容易的。正如本章开头所描述的那样，相等大小的两个堆的“ 合并”就是公共位置 p 的 两棵子树的合并，可以简单地通过 p 元组的下堆来完成，正如键值 14 在图 9-5f ～ 图 9-5g 中 所发生的变化。

在使用数组来表示堆时，如果我们初始化时将 n 个元组以任意顺序存储在数组中， 就能够通过一个单层循环来实现自底向上的堆构造， 该循环在树的每个位置上调用 _downheap 。并且这些调用是有序进行的，从最底层开始并在树的根节点处结束。事实上，由于下堆被调 用对叶节点无影响， 因此这些循环可以从最底层的非叶节点开始。

在代码段 9-6 中， 我们对 9.3.4 节的原始类 HeapPriorityQueue 进行了加强，从而支持 一个初始化集合自底向上堆构造。我们介绍了一个非公有的方法_heapify , 它在每个非叶位置上调用 _downheap , 从最底层开始，直到树的根节点结束。我们已经重新设计了该类的构造函数，以使其能接收一个可选的参数，该参数可以是任何 (k, V) 元组的序列。我们使用列表理解语法（见 1.9.2 节）来建造一个由给定内容的组合元组构成的初始化列表，而不是将 self._data 初始化为一个空列表。我们声明了一个空序列作为参数的默认值，作为 HeapPriorityQueue(） 默认的语法，使其能够处理空的优先级队列并输出结果。

def __init__ (self, contents=()):
”””
Create a new priority queue.
By default, queue will be empty. If contents is given, it should be as an
iterable sequence of (k,v) tuples specifying the initial contents.
”””
  self._data = [ self._Item(k,v) for k,v in contents ] # empty by default
  if len(self. data) > 1:
    self._heapify()
def _heapify(self):
  start = self._parent(len(self) − 1) # start at PARENT of last leaf
  for j in range(start, −1, −1): # going to and including the root
    self._downheap(j)

自底向上堆构建的渐近分析

自底向上堆构建比向一个初始的空堆中逐个插入 n 个键值元组要更快，而且是渐近式的。直观地说，我们是在树的每个位置上进行单个的下堆操作，而不是单个的上堆操作。由于与树底部更近的节点多于离顶部近的，向下路径的总和是线性变化的，正如下面的命题所示。

命题 9-3: 假设两个键值可以在 O(1) 的时间内完成比较，则使用 n 个元组自底向上构 建堆需要的时间复杂度为 O(n) 。

证明： 构建堆的主要成本是在每个非叶节点位置下堆的构造步骤上。用 \(\pi_v\) 表示堆从非叶节点 v 到其 “中序后继“ 叶节点的路径，也就是说，该路径是从 v 节点开始，沿着 v 的右孩子，然后继续沿着最左方向下直至到达叶节点。虽然 \(\pi_v\) 不需要一定是从 v 节点向下冒泡步骤产生的路径，但是它的长度 \(||\pi_v||\)（即 \(\pi_v\) 的边的个数） 与以 v 为根的子树的高度成比例， 因此，这也是节点 v 下堆操作的复杂度的边界。我们用路径大小的总和 \(\sum_v||\pi_v||\) 来限制自底向上堆构造算法总的运行时间。直观地，图 9-6 展示了 “可视化” 的证明，用标签标记非叶节点 v 的路径 \(\pi_v\) 中所包含的每条边。

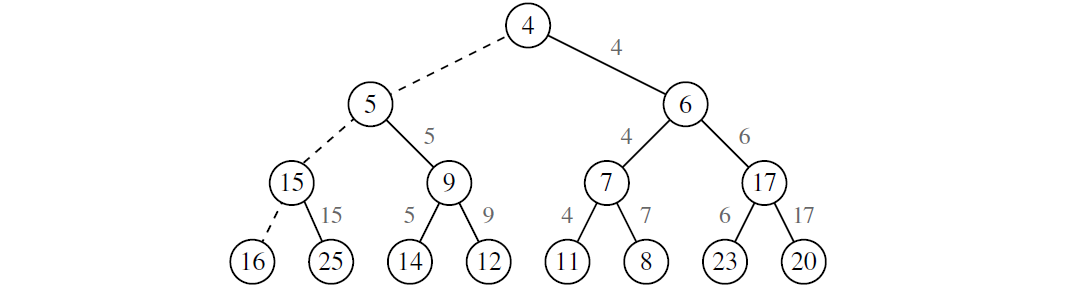
图 9-6 自底向上堆构建运行时间为线性的“可视化”证明。路径 \(\pi_v\) 所包含的每条边 e（如果有的话）都加上含有节点 v 的标签

我们声明对于所有非叶节点 v 的路径 \(\pi_v\) 是不相交的，因此路径长度的和受到树的总边数的限制，即为 O(n) 。为了展示这一结论，我们考虑两个定义：

1. 向左学习（left-learning）：指在下堆操作中，一次向父节点的左孩子下堆的过程
2. 向右学习（right-learning）：指在下堆操作中，一次向父节点的右孩子下堆的过程

一个特别的向右学习边 e 只能是节点 v 的路径 \(\pi_v\) 的一部分，在由 e 表示的关系中，该节点 v 是父节点。如果持续地向左向下直至到达叶节点，那么所到达的叶节点可以用来对向左学习的边进行划分。每个非叶节点只使用在同组中的向左学习边将生成非叶节点的中序后继。由于每个非叶节点必须有不同的中序后继，因此没有两个路径包含相同的向左学习边。因此，我们断定自底向上构造堆的时间复杂度为 O(n)

9.3.7 python 的 heapq 模块

python 的标准分布包含一个 heapq 模块，该模块提供对基于堆的优先级队列的支持。该模块不提供任何优先级队列类，而是提供一些函数，这些函数把标准 python 列表作为堆进行管理。它的模型与我们自己的基本相同： 基于层次编号的索引，将 n 个元素存储在 \(L[0]\sim L[n - 1]\) 的单元中，并且最小元素存储在根 \(L[0]\) 中。我们注意到 heapq 并不是单独地管理相关的值，即元素作为它们自己的键值。

Heapq 模块支待如下函数，假设所有这些函数在调用之前，现有的列表 L 已经满足 heap-order 属性：

• heappush(L, e)：将元素 e 存入列表 L, 并重新调整列表以满足 heap-order 属性。该函数执行的时间复杂度为 O(\(\log n\)) 。

• heappop(L) ：取出并返回列表 L 中拥有最小值的元素，并且重新调整存储以满足 heap -order 属性。该函数执行的时间复杂度为 O(\(\log n\)) 。

• heappusbpop(L, e) ：将元素 e 存入列表 L 中，同时取出和返回最小的元组。该函数执行的时间复杂度为 O(\(\log n\)) ， 但是它较分别调用 push 和 pop 方法的效率稍微高一些， 因为列表的大小在处理过程中不发生变化。如果最新被插入列表的元素值是最小的， 那么该函数立刻返回；否则，新增的元素将会替换在根节点处取出的元素，随后，函数会执行下堆操作。

• heapreplace(L, e) ： 与 heappushpop 方法相类似，但相当于在插入操作前执行 pop 操 作（换言之，即使新插入的元素是最小值也不能被返回） 。该函数执行的时间复杂度为 O( \(\log n\)) ，但是它比分别调用 push 和 pop 方法效率更高。

该模块还支持在不满足 heap-order 属性的序列上进行操作的其他函数。

• heapify(L) ： 改变未排序的列表，使其满足 heap-order 屈性。这个函数使用自底向上的堆构造算法，时间复杂度为 O(n) 。

• nlargest(k, iterable) ：从一个给定的迭代中生成含有 k 个最大值的列表。执行该函数的时间复杂度为 O(\(n + k \log n\)) ，这里使用 n 来表示迭代的长度（见练习 C-9.42 ) 。

• nsmallest(k, iterable) ：从一个给定的迭代中生成含有 k 个最小值的列表。该函数使用与 nlargest 相同的技术，其时间复杂度为 O(\(n + k \log n\))

9.4 使用优先级队列排序

在定义优先级队列 ADT 时，我们注意到任何类型的对象都能够被定义为键，但是任何一对键之间必须是可比较的，这样这个键集自然是可排序的。在 python 中，我们常用 “＜＂ 操作符来定义这样的序列，在定义过程中，必须满足属性：

• 漫反射特性： \(k \nless k\) 。
• 传递属性：如果 \(k_1 < k_2\), 并且 \(k_2 ＜ k_3\)，则 \(k_1 < k_3\)

这种关系被正式地定义为严格弱序( strict weak order ) ，因为它允许各个键值是相等的， 但更广泛的等价类是完全有序的，因为它们可以根据传递属性排列成唯一的从最小值到最大 值的序列。

作为优先级队列的第一个应用，我们展示了它们如何被用在对一个可比较元素集合 C 的排序上。也就是说，我们能够生成集合 C 中元素的一个递增排序的序列（或者如果存在重复数据，则至少是非递减的顺序） 。这个算法非常简单一一我们将所有元素插入一个最初为空的优先级队列中，然后重复调用 remove_min, 从而以非递减的顺序获取所有元素。

我们在代码段 9-7 中给定了这种算法的一个实现，其中假定 C 是一个位置列表（见 7.4 节） 。调用方法 P.add 时，我们把集合的原始元素 element 同时作为键和值，即 P.add(element, element) 。

def pq_sort(C):
   ”””Sort a collection of elements stored in a positional list.”””
   n = len(C)
   P = PriorityQueue( )
   for j in range(n):
      element = C.delete(C.first())
      P.add(element, element) # use element as key and value
   for j in range(n):
      (k,v) = P.remove_min()
      C.add_last(v) # store smallest remaining element in C

代码片段 9.7：pq_sort 函数的实现，假定 PriorityQueue 类的适当实现。 请注意，输入列表 C 的每个元素在优先级队列 P 中充当其自己的键

如果对以上代码做个小小的改动：将元素按照一定的规则排序而不是保留其默认的顺序，这样便可以使该函数更为通用。例如，当处理字符串时，＂＜＂操作符定义一个字典序列，这是将一个字母序扩展到 Unicode 上。比如，我们定义 '2' < '4' ，因为是根据每个字符串的第一个字母的顺序定义的，就像 'apple' < 'banana' 一样。假设有一个应用，在应用中我们有一个众所周知的代表整数值（如 '12') 的字符串列表，那么我们的目标就是根据这些对应的整数值给这些字符串排序。

python 中提供了为一个排序算法自定义顺序的标准方法，作为排序函数的一个可选参数，一个对象自身就是为一个给定的元素计算键的单参数函数（见 1.5 和 1.10 节，在内置 max 函数的上下文中有关于该方法的讨论） 。比如，在使用一个（数字）字符串列表时，我们很可能希望将 int (s) 的数值作为列表中字符串 s 的键。在这种情况下， int 类的构造函数可以作为计算键的单参数函数。在这种方式下，字符串 '4' 将排在字符串 '12' 的前面，因为它们的键的关系是 int('4') < int('12'） 。我们把用这种的方法为 pq_sort 函数提供可选键参数的 问题留作一个练习（见练习 C-9.46)

9.4.1 选择排序和插入排序

对于任意给定的优先级队列类的有效实现， pq_sort 函数都能正确地处理。但是，排序算法的运行时间复杂度取决于给定的优先级队列类的 add 方法和 remove_min 方法的时间复杂度。接下来我们讨论一种优先级队列的实现，该实现实际上使得 pq_sort 计算成为经典的 排序算法之一。

选择排序

如果用一个未排序的列表实现 P , 那么由于每增加一个元素都能在 O(1) 的时间复杂度内完成，所以在 pq_sort 的第一阶段所花费的时间复杂度为 O(n) 。在第二阶段，每次 remove_min 操作的时间复杂度与 P 的大小成正比。因此，计算的瓶颈是在第二阶段重复地选择最小元素。由于这个原因，这 个算法被命名为选择排序（见图 9-7 ) 。

如上面提到的，算法的瓶颈就是我们在第二阶段重复地从优先级队列 P 中移除 拥有最小键值的元组。P 的大小开始为 n, 随着每次调用remove_min, 持续递减，直到变为 0 。所以， 第一次操作的时间复杂度为 O(n) ， 第二次操作的时间复杂度为 O(n - 1) ，以此类推。因此，第二阶段所需要的总时间为：

\[ O(n+(n-1)+...+2+1)=O(\sum^n_{i=1}i) \]

由命题 3-3 可知， \(\sum^n_{i=1}i = n(n+ 1 )/2\) 这一结论。因此，第二阶段的时间复杂度为 O(\(n^2\)) ，故整个选择排序算法的时间复杂度为 O(\(n^2\))

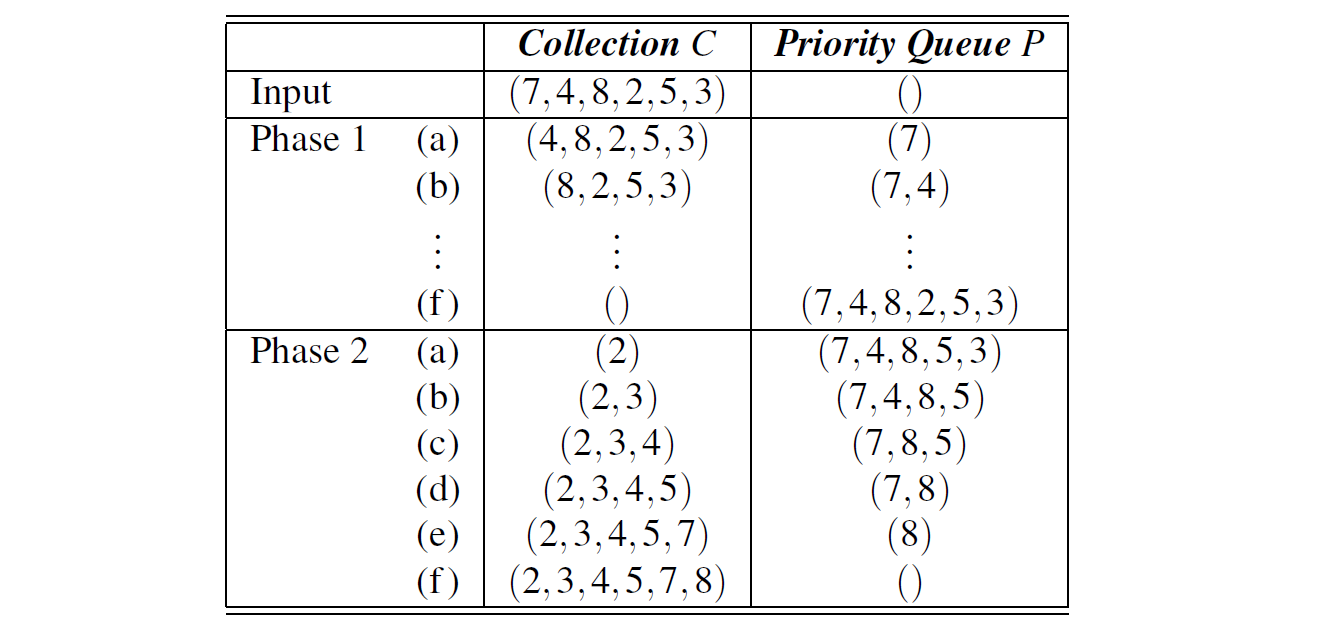
图 9.7：对集合 C = (7,4,8,2,5,3) 执行选择排序。

插入排序

如果用一个排序列表实现优先级队列，由于此时每次在 P 上执行 remove_ min 操作所花费的时间复杂度为 O(1) ， 因 此我们可以将第二阶段的时间复杂度降低到 O(n) 。不幸的是，第一阶段将会变成整个算法的瓶颈，因为在最坏情况下，每次 add 操作的时间复杂度与当前 P 的大小成正比。这种排序算法被称作插入排序（ 见图 9-8) 。实际上，在优先级队列中增加一个元素的实现与之前 7.5 节给出的插入算法的步骤几乎完全相同。

插入排序算法的第一阶段在最坏情况下的运行时间为：

\[ O(n+(n-1)+...+2+1)=O(\sum^n_{i=1}i) \]

同样，根据命题 -2, 这意味着最坏情况下第一阶段的时间复杂度为 O(\(n^2\)) ，并且整个插入排序算法的时间复杂度也为 O(\(n^2\))。但是，不同于选择排序，插入排序在最好情况下的时间复杂度为 O(n) 。

9.4.2 堆排序

正如我们之前所看到的，使用堆实现的优先级队列比较有优势，因为优先级队列 ADT 中的所有方法都是在对数级时间或更短时间内完成。因此，这种实现非常适合那些所有优先级队列方法都追求快速的运行时间的应用。现在，让我们再次考虑 pq_sort 的设计，这次使 用基于堆的优先级队列的实现方式。

在第一阶段，由于第 i 次 add 操作完成后堆有 i 个元组，所以第 i 次 add 操作的时间复杂度为 O( \(\log i\)) 。因此，这一阶段整体的时间复杂度为 O(\(n \log n\)) （采用 9.3.6 节所描述的自底向上堆构造的方法，第一阶段的时间复杂度能够被提升到 O(n) ） 。

在 pq_sort 的第二阶段，由于在第 j 次 remove_min 操作执行时堆中有( \(n -j+ 1\) ) 个元组，因此第 i 次 remove_min 操作的时间复杂度为 O(\(\log(n － j+1 )\)） 。将所有这些 remove_min 操作累加起来，这一阶段的时间复杂度为 O(\(n \log n\)) 。所以，当使用堆来实现优先级队列时， 整个优先级队列排序算法的时间复杂度为 O(\(n \log n\)) 。这个排序算法就称为堆排序， 以下命题总结了它的性能。

命题 9-4: 假设集合 C 的任意两个元素能在 O(1) 时间内完成比较，则堆排序算法能在 O(\(n\log n\)) 时间内完成含有 n 个元素的集合 C 的排序。

显然，堆排序的 O(\(n\log n\)) 时间复杂度比起选择排序和插入排序（见 9.4.1 节）的 O(\(n^2\)) 时间复杂度性能是相当好的。

实现原地堆排序

如果集合 C 的排序由基于数组序列的方法实现， python 列表就是一个典型的代表，我们可以通过引入一个常量因子以列表自身的一部分存储堆的方法来加速堆排序并减小空间需求，以避免使用辅助堆数据结构。这可以通过如下所示的算法修改进行实现：

1. 通过使每个位置的键值不小于其孩子节点的键值，我们重新定义堆的操作，使其成为面向最大值的堆( maximum-oriented heap ) 。这可以通过重新编码算法或者调整键的概念为相反方向的来实现。在算法执行过程中的任意时间点，我们始终使用 C 的左半部分（即 0 到一个确定的索引 i - 1 ) 来存储堆中的元组，并且使用 C 的右半部分（即索引 i ~ n - 1 ) 来存储序列的元素。也就是说， C 的前 i 个元素（在索引 0 , ···, i - 1 处）提供了堆的数组列表表示。

2) 在算法的第一阶段，我们从一个空堆开始，并从左向右移动堆与序列之间的边界， 一次一步。在第 i 步 ，这里 i = 1 , … ， n ，我们通过在索引 i - 1 处追加元素来对堆进行扩展。 3) 在算法的第二阶段， 我们从一个空的序列开始，并从右到左移动堆与序列之间的边界， 一次一步。在第 i 步，这里 i = 1 , … , n , 我们将最大值元素从堆中移除并将其存储到索引为 n - i 的位置上。

一般来说，如果一个排序算法除了存储对象已排序的序列，仅额外使用一小部分内存， 我们就说该算法为原地 (in-place) 算法。上述调整过的堆排序算法就是原地算法。相对于将元素移出序列再重新移入，我们简单地对序列进行了重新组织。我们在图 9-9 中对原地堆排序第二阶段的处理过程进行了说明。

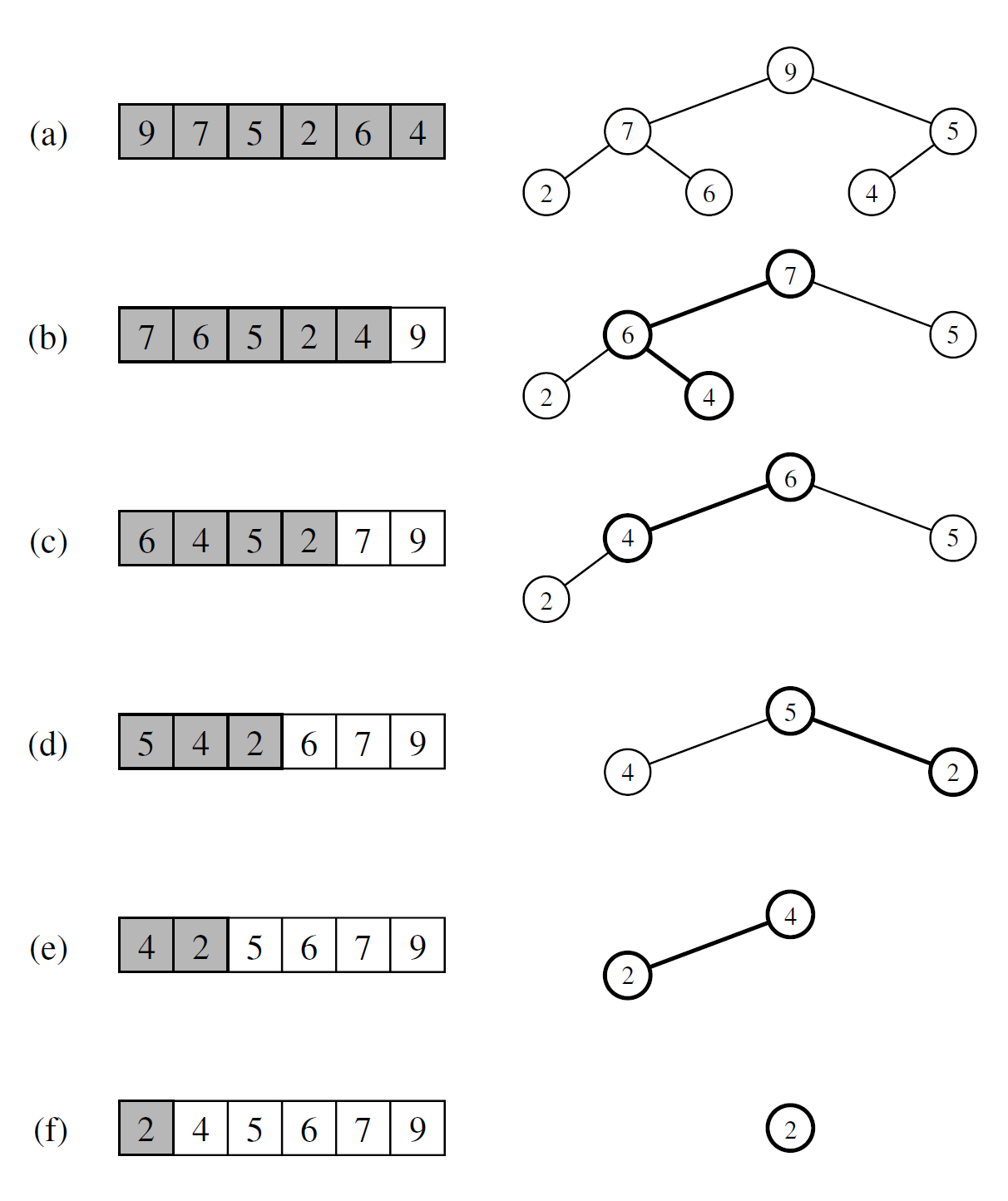
图 9.9：就地堆排序的第 2 阶段。 每个序列表示的堆部分被突出显示。 每个序列（隐含地）表示的二叉树用图表突出显示了最近的堆下冒泡路径。

9.5 适应性优先级队列

9.1.2 节给出的优先级队列 ADT 的方法对于大多数优先级队列的基本应用（比如排序） 来说巳经很完善了。但是，有些场景还需要一些附加方法，比如下面所示的涉及航班候补等待( standby ) 乘客的应用场景。

• 持有消极态度的待机乘客可能会因为对等待感到疲倦而决定在登机时间到来之前离开，并请求从等待列表中移除。因此，我们将与该乘客相关的元组从优先级队列中移除。由于要离开的乘客不需要最高优先级，因此 remove_min 操作不能完成此任务。所以，我们需要一个新的操作 remove , 用来删除优先级队列中的任意一个元组。
• 另一个待机乘客拿出她的常飞乘客金卡并出示给售票代理，因此她的优先级将被相应地更改。为了完成这个优先级的变更，我们需要一个新的操作 update, 使我们能用一个新的键去替换元组现有的键。

在实现 14.6.2 节和 14.7.1 节的特定图算法时，我们将看到可适应性优先级队列的另一 种应用。在本节中，我们构建了一个可适应性优先级队列 ADT, 并展示了如何将这个抽象概念作为基于堆的优先级队列的扩展来实现。

9.5.1 定位器

为了有效地实现方法 update 和 remove, 我们需要一种在优先级队列中找到用户元组的机制，该机制可以避免在整个元组集合进行线性搜索。为了实现这一目标，当一个新的元素追加到优先级队列中时，我们返回一个特殊的对象给调用者，该对象称为定位器( locator ) 。对于一个优先级队列 P, 当执行 update 或者 remove 方法时，我们需要用户提供一个合适的定位器作为参数，详情如下：

• P.update(loc, k, v) ： 用定位器 loc 代替键和值作为元组的标识。
• P.remove(loc) ： 从优先级队列中删除以 loc 标识的特定元组，并返回它的 ( key, value ) 对

定位抽象类似于我们从 7.4 节开始使用的位置列表 ADT 中使用的位置抽象和第 8 章介绍的树的 ADT 中使用的位置抽象。但是，定位器和位置不同，因为优先级队列的定位器并不代表结构中一个元素的具体位置。在优先级队列中， 一些看似与元素没有直接关系的操作， 一旦执行，该元素可能在数据结构中被重新定位。只要一个元组项一直在队列中的某个地方，这个元组的定位器将一直有效

9.5.2 适应性优先级队列的实现

在本节中，我们提供一个可适应性优先级队列的 python 实现，将它作为 9.3.4 节所讨论的 HeapPriorityQueue 类的扩展。为了实现 Locator 类，我们将扩展现有 _Item 的组成来增加一个额外的字段，该字段指定在基于数组表示的堆中的元素的当前索引，如图 9-10 所示

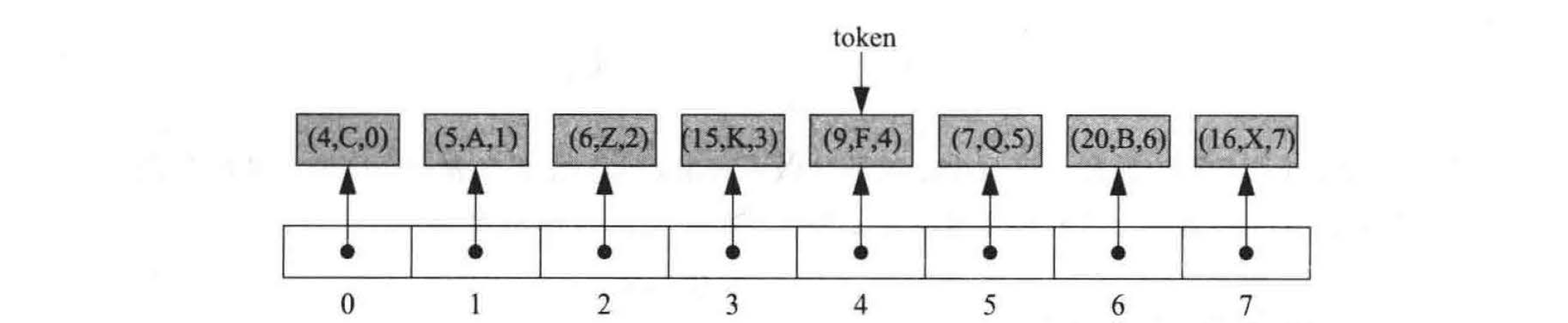
图 9-10 用一个定位器序列表示堆。数组中每个元组的索引对应每个定位器实例中的第三个元素。假定标识符 token 是用户域中的一个定位器的引用 (reference)

该列表是一个指向定位器实例的序列， 每个定位器都存储一个 key, value 和列表内元组的当前索引。用户会获得每个插入的元素的定位器实例的引用，如图 9-10 中的 token 标识所示。

在堆上执行优先级队列操作时，元组在结构中被重新定位，我们重新设置列表中各定位器实例的位置，并更新每个定位器的第三个字段以反映该定位器在列表中的新索引。图 9-11 展示了上述的堆在调用 remove_min() 方法后状态的一个例子。堆操作使得最小元组 (4, C) 被删除， 并使元组 (16, X) 暂时从最后一个位置移到根位置，这之后是向下冒泡的处理阶段。在下堆阶段，元素 (16, X) 与它在列表索引为 1 的位置的左孩子 ( 5, A ) 做了交换，然后又与它在列表的索引值为 4 的右孩子元组 ( 9 , F ) 交换。在最后的配置中，所有受影响的元组的定位器实例都已经被修改了，以反映它们的新位置。

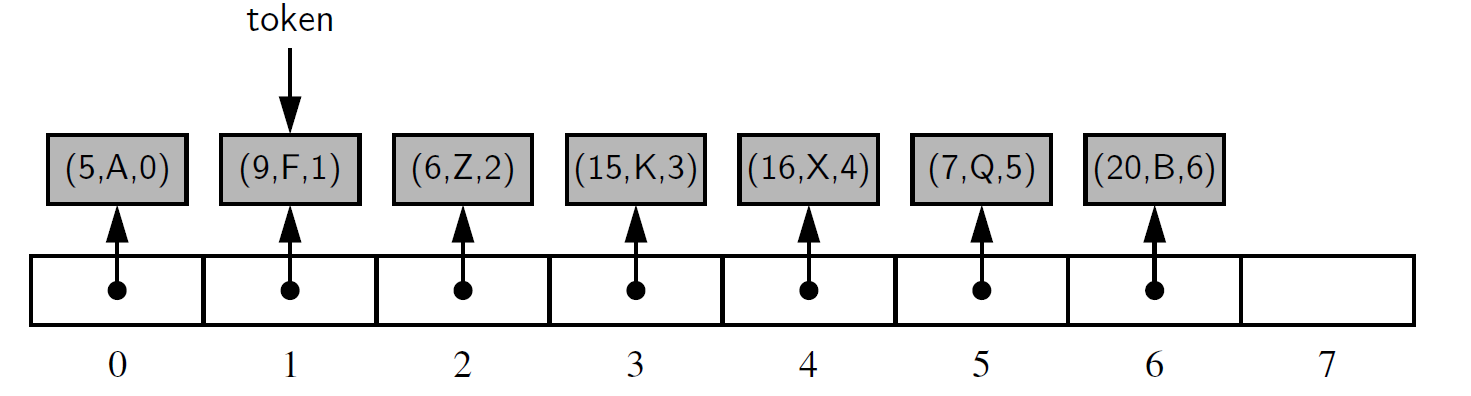
图 9.11：在图 9.10 中最初描绘的堆上调用 remove_min() 的结果。 标识符 token 继续引用与原始配置中相同的定位器实例，但该定位器在列表中的位置已更改，定位器的第三个字段也是如此

强调定位器实例没有改变元组标识非常重要。如图 9-10 和图 9-11 所示，用户 token 的指针将继续指向相同的实例。我们只是简单地改变了实例的第三个域，并改变了列表序列中引用该实例的索引的位置。

通过这种新的表示， 对可适应性优先级队列 ADT 提供额外的支持更加直接。当一个定位器实例被当作参数传给方法 update 或 remove 时， 我们可以借助该结构的第三个域来指明该元素在堆中的位置。根据前面的讨论我们知道， 一个键的 update 操作仅需要简单的一次堆向上行泡或堆向下冒泡来重新满足 heap-order 属性（完全二叉树属性保持不变） 。为了实现移除任意一个元素的操作，我们把在最后位置的元素移到腾空的位置，并再次执行适当的冒泡操作来满足 heap-order 属性。

python 实现

代码段 9-8 和代码段 9-9 展示了可适应性优先级队列的 python 实现，它是 9.3.4 节 HeapPriorityQueue 类的子类。我们在原始类上做的修改非常小。我们定义了一个公有的 Locator 类，该类继承非公有的＿Item 类并通过额外的＿index 域增强它。之所以将它定义为公有类，是因为我们要同时用 locators 作为返回值和参数， 但是，用户定位器类的公有接口不包括任何其他功能。

为了在堆操作的过程中更新定位器， 我们借助一个特定的设计决策， 即在原始类在所有数据移动中都使用一个非公有的方法＿swap 。在两个互换的定位器实例中， 我们重写该实用程序来执行更新定位器中所存储的索引的附加步骤。

我们提供一个新的＿bubble 程序，该程序负责一个在堆中任意位置的键改变时恢复 heap-oder 属性，不管这个改变是由于键的更新，还是因为从树的最后一个位置移除元素及其对应的元组。＿bubble 程序根据给定的位置是否有一个更小的父节点来决定是否进行堆向上冒泡或者堆向下冒泡（如果一个更新的键恰巧保存了有效的当前位置，我们在技术上调用 _downheap 但没有交换结果） 。

代码段 9-9 给出了公有的方法。现有的 add 方法被覆盖，两者都是使用一个 Locator 实例（而不是存储新元素的＿Item 实例），并将定位器返回给调用者。该方法的其余部分与原有的方法相类似， 即通过＿swap 新版本的使用来制定管理定位器的索引。由于对于可适应性 优先级队列在行为上唯一需要的改变已经在重载＿swap 方法中提供，因此没有必要再重写 remove_min 方法。

update 和 remove 方法为可适应性优先级队列提供了核心的新功能。我们对一个被调用方发送的定位器的有效性进行鲁棒性检查（为了节省篇幅， 我们给出的代码不做确保参数确实是一个 Locator 实例的初步类型检查） 。为了确保定位器与给定优先级队列中的当前元素相关联，我们检查被封装在定位器对象中的索引， 然后验证在该索引处的列表的元组正是这个定位器。

综上所述， 可适应性优先级队列提供了与非可适应性版本相同的渐近效率和空间使用， 并且为新的基于定位器的 update 和 remove 方法提供了对数级的性能。表 9-4 给出了性能总结。

from .heap_priority_queue import HeapPriorityQueue

class AdaptableHeapPriorityQueue(HeapPriorityQueue):
  """A locator-based priority queue implemented with a binary heap."""

  #------------------------------ nested Locator class ------------------------------
  class Locator(HeapPriorityQueue._Item):
    """Token for locating an entry of the priority queue."""
    __slots__ = '_index'                 # add index as additional field

    def __init__(self, k, v, j):
      super().__init__(k,v)
      self._index = j

  #------------------------------ nonpublic behaviors ------------------------------
  # override swap to record new indices
  def _swap(self, i, j):
    super()._swap(i,j)                   # perform the swap
    self._data[i]._index = i             # reset locator index (post-swap)
    self._data[j]._index = j             # reset locator index (post-swap)

  def _bubble(self, j):
    if j > 0 and self._data[j] < self._data[self._parent(j)]:
      self._upheap(j)
    else:
      self._downheap(j)

  #------------------------------ public behaviors ------------------------------
  def add(self, key, value):
    """Add a key-value pair."""
    token = self.Locator(key, value, len(self._data)) # initiaize locator index
    self._data.append(token)
    self._upheap(len(self._data) - 1)
    return token

  def update(self, loc, newkey, newval):
    """Update the key and value for the entry identified by Locator loc."""
    j = loc._index
    if not (0 <= j < len(self) and self._data[j] is loc):
      raise ValueError('Invalid locator')
    loc._key = newkey
    loc._value = newval
    self._bubble(j)

  def remove(self, loc):
    """Remove and return the (k,v) pair identified by Locator loc."""
    j = loc._index
    if not (0 <= j < len(self) and self._data[j] is loc):
      raise ValueError('Invalid locator')
    if j == len(self) - 1:                # item at last position
      self._data.pop()                    # just remove it
    else:
      self._swap(j, len(self)-1)          # swap item to the last position
      self._data.pop()                    # remove it from the list
      self._bubble(j)                     # fix item displaced by the swap
    return (loc._key, loc._value)

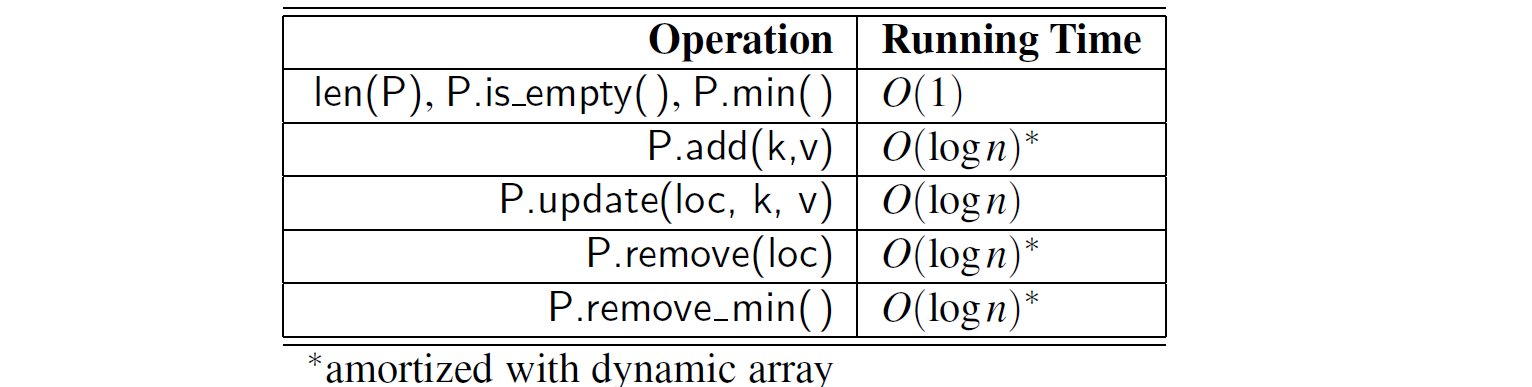
表 9.4：大小为 n 的自适应优先级队列 P 的方法的运行时间，通过我们基于数组的堆表示实现。 空间要求为 O(n)。