Autograd mechanics — PyTorch 2 3 documentation

这篇说明将概述 autograd 如何运行以及记录操作。虽然没有必要掌握所有细节，但我们建议您熟悉这些内容，因为这有助于编写更高效、清晰的程序，并能在调试中提供帮助。

Autograd 如何记录历史

Autograd 是一种反向自动微分系统。从概念上讲，autograd 在您执行操作的同时会记录一张包含所有创建数据操作的图，并形成一个有向无环图（DAG），其叶节点是输入张量，根节点是输出张量。通过从根节点追溯到叶节点，您可以自动使用链式法则计算梯度。

在内部，autograd 使用 Function 对象（实际是表达式）来表示这张图，通过 apply() 方法可以计算该图的输出。在计算正向传递的同时，autograd 会执行所请求的计算并构建一张图，用于计算梯度（每个 torch.Tensor 的 .grad_fn 属性就是该图的入口）。当正向传递完成后，我们会在反向传递中评估这张图以计算梯度。

值得注意的是，这张图在每次迭代时都会从头开始重建，这使得我们可以使用任意的 Python 控制流语句，从而在每次迭代时更改图的整体形状和大小。您无需在启动训练之前预先编码所有可能的路径——运行的内容就是您需要微分的内容。

已保存的张量

某些操作在正向传递期间需要保存中间结果，以在反向传递中执行。例如，函数 \( x \mapsto x^2 \) 会保存输入 \( x \) 以计算梯度。

在定义自定义 Python Function 时，可以使用 save_for_backward() 在正向传递中保存张量，并通过 saved_tensors 在反向传递中检索它们。有关详细信息，请参阅 扩展 PyTorch。

对于 PyTorch 定义的操作（如 torch.pow()），需要时会自动保存张量。为了学习或调试的目的，可以通过查找其以 _saved 为前缀的属性，查看特定 grad_fn 保存了哪些张量。

x = torch.randn(5, requires_grad=True)
y = x.pow(2)
print(x.equal(y.grad_fn._saved_self))  # True
print(x is y.grad_fn._saved_self)  # True

在上面的代码中，y.grad_fn._saved_self 指向与 x 相同的张量对象，但情况并非总是如此。例如：

x = torch.randn(5, requires_grad=True)
y = x.exp()
print(y.equal(y.grad_fn._saved_result))  # True
print(y is y.grad_fn._saved_result)  # False

在内部，PyTorch 保存张量时使用打包机制以防止引用循环，然后在读取时解包为不同的张量。在此例中，y.grad_fn._saved_result 中获取的张量对象与 y 并不相同（但它们共享相同的存储）。

张量是否会被打包成不同的张量对象取决于它是否是其自身 grad_fn 的输出，这是实现细节，可能会发生变化，不应作为依赖。

您可以通过 已保存张量的钩子 来控制 PyTorch 如何打包/解包。

非可微函数的梯度

自动微分中的梯度计算仅在每个使用的基本函数均可微时才有效。然而，许多实际使用的函数不具有这一性质（例如 relu 或 sqrt 在 0 处）。为了尽量减少非可微函数的影响，我们按照以下规则定义基本操作的梯度：

1. 如果函数在当前点可微并且存在梯度，则直接使用该梯度。

2. 如果函数是凸的（至少局部凸），使用最小范数的次梯度（这是最陡下降方向）。

3. 如果函数是凹的（至少局部凹），使用最小范数的上梯度（考虑 -f(x) 并应用前一点）。

4. 如果函数定义明确，通过连续性在当前点定义梯度（此处可能为无穷，例如 sqrt(0)）。若存在多个可能值，则随机选取一个。

5. 如果函数未定义（例如 sqrt(-1)、log(-1) 或在输入为 NaN 时的大多数函数），所用的梯度值是任意的（我们可能会抛出错误，但不保证一定如此）。大多数函数会将梯度设为 NaN，但出于性能原因，部分函数会使用其他值（例如 log(-1)）。

6. 如果函数不是确定性映射（即不是一个数学函数），则会被标记为不可微分。如果在需要梯度的张量上使用此函数且不在 no_grad 环境中，它会在反向传播时抛出错误。

局部禁用梯度计算

在 Python 中有几种机制可以局部禁用梯度计算：

为了禁用整个代码块的梯度计算，可以使用无梯度模式（no-grad mode）和推理模式（inference mode）这类上下文管理器。对于更精细地从梯度计算中排除子图，可以设置张量的 requires_grad 属性。

除了讨论上述机制外，我们还描述了评估模式（nn.Module.eval()）。尽管它不用于禁用梯度计算，但其名称常与其他三者混淆。

设置 requires_grad

requires_grad 是一个标志，默认情况下为 False（除非包含在 nn.Parameter 中），用于细粒度地将子图从梯度计算中排除。它在正向和反向传递中都会生效：

在正向传递中，只有当操作的至少一个输入张量需要梯度时，才会记录该操作。在反向传递（.backward()）中，只有 requires_grad=True 的叶张量才会将梯度累积到它们的 .grad 字段。

需要注意的是，即使每个张量都有此标志，设置它仅对叶张量（没有 grad_fn 的张量，例如 nn.Module 的参数）有效。非叶张量（具有 grad_fn 的张量）关联了反向传播图，因此它们的梯度是计算需要梯度的叶张量的梯度的中间结果。从定义上看，所有非叶张量都自动具有 requires_grad=True。

设置 requires_grad 应该是您控制模型的哪些部分参与梯度计算的主要方式。例如，如果需要在模型微调期间冻结预训练模型的部分参数，可以直接将不希望更新的参数设为 .requires_grad_(False)。正如上文所述，由于这些参数作为输入的计算不会记录在正向传递中，因此在反向传递中它们的 .grad 字段不会更新，因为它们最初就不在反向传播图中。

由于这种模式很常见，requires_grad 也可以在模块级别通过 nn.Module.requires_grad_() 设置。对模块应用 .requires_grad_() 会影响该模块的所有参数（默认情况下 requires_grad=True）。

Grad Modes

Apart from setting requires_grad there are also three grad modes that can be selected from Python that can affect how computations in PyTorch are processed by autograd internally: default mode (grad mode), no-grad mode, and inference mode, all of which can be togglable via context managers and decorators.

Mode	Excludes operations from being recorded in backward graph	Skips additional autograd tracking overhead	Tensors created while the mode is enabled can be used in grad-mode later	Examples
default			✓	Forward pass
no-grad	✓		✓	Optimizer updates
inference	✓	✓		Data processing, model evaluation

默认模式（梯度模式）

“默认模式”是我们在未启用无梯度模式或推理模式时所处的模式。与“无梯度模式”相对比，默认模式有时也称为“梯度模式”。

默认模式最重要的一点是，这是唯一一个 requires_grad 属性生效的模式。在无梯度模式和推理模式中，requires_grad 都会被强制设置为 False。

无梯度模式

在无梯度模式中，计算会表现得好像没有输入需要梯度一样。换句话说，即使输入张量设置了 requires_grad=True，在无梯度模式中的计算也不会记录在反向传播图中。

如果需要执行一些操作，这些操作不应由 autograd 记录，但您仍想在稍后以梯度模式使用这些计算的输出，此时可以启用无梯度模式。这个上下文管理器方便地让您禁用一段代码或函数的梯度，而无需临时将张量的 requires_grad 属性设置为 False 再恢复为 True。

例如，无梯度模式在编写优化器时很有用：执行训练更新时，您希望对参数进行就地更新，而无需让 autograd 记录该更新。您还打算在下一次前向传递中以梯度模式使用更新后的参数。

在 torch.nn.init 中的实现也依赖于无梯度模式，以避免在初始化参数时，由 autograd 跟踪就地更新的已初始化参数。

推理模式

推理模式是无梯度模式的增强版本。与无梯度模式一样，推理模式中的计算不会记录在反向传播图中，但启用推理模式可以进一步加快模型的运行速度。这个性能提升带来了一个缺点：在推理模式中创建的张量在退出推理模式后无法用于由 autograd 记录的计算中。

如果您在执行的计算不需要记录在反向传播图中，且您不打算在后续的任何由 autograd 记录的计算中使用推理模式创建的张量，那么可以启用推理模式。

建议您在代码中不需要 autograd 跟踪的部分（例如数据处理和模型评估）尝试使用推理模式。如果您的用例直接奏效，那就是免费的性能提升。如果启用推理模式后出现错误，请检查您是否在退出推理模式后，将推理模式创建的张量用于由 autograd 记录的计算中。如果无法避免这种情况，可以随时切换回无梯度模式。

有关推理模式的详细信息，请参阅 推理模式。

有关推理模式的实现细节，请参阅 RFC-0011-InferenceMode。

评估模式 (nn.Module.eval())

评估模式并不是一种局部禁用梯度计算的机制，但仍在此列出，因为它有时会被误认为是禁用梯度的方式。

从功能上讲，module.eval()（或等价的 module.train(False)）与无梯度模式和推理模式完全无关。model.eval() 如何影响您的模型，完全取决于模型中使用的特定模块以及它们是否定义了训练模式相关的行为。

如果您的模型依赖于可能根据训练模式有不同行为的模块（例如 torch.nn.Dropout 和 torch.nn.BatchNorm2d），请确保自行调用 model.eval() 和 model.train()，以避免在验证数据上更新 BatchNorm 的运行统计信息。

即使您不确定模型是否具有训练模式相关的行为，建议您在训练时始终使用 model.train()，在评估时（验证/测试）使用 model.eval()。因为您使用的模块可能会更新，从而在训练和评估模式中表现不同。

使用 Autograd 的就地操作

在 autograd 中支持就地操作非常困难，在大多数情况下我们不建议使用。autograd 具有积极的缓冲区释放和重用策略，使其非常高效，几乎没有情况能够通过就地操作显著降低内存使用。除非在极高的内存压力下操作，否则几乎不需要使用它们。

就地操作适用范围受限的两个主要原因是：

1. 就地操作可能会覆盖计算梯度所需的值。

2. 每个就地操作都要求实现重写计算图。非就地版本会分配新对象并保留对旧图的引用，而就地操作则要求更改代表该操作的 Function 所有输入的创建者。这可能很棘手，尤其是当许多张量共享相同的存储空间时（例如，通过索引或转置创建）。如果其他任何 Tensor 引用了已修改输入的存储空间，就地函数会引发错误。

就地正确性检查

每个张量都有一个版本计数器，在任何操作中标记为已更改时，该计数器都会递增。当 Function 保存任何张量用于反向传播时，会同时保存其包含张量的版本计数器。一旦您访问 self.saved_tensors，它就会被检查，如果其值大于已保存的值，将引发错误。这确保了如果您使用就地函数且未看到任何错误，可以确信计算的梯度是正确的。

多线程 Autograd

autograd 引擎负责执行所有反向操作以完成反向传播。本节将描述在多线程环境中如何最好地利用它的所有细节（这仅适用于 PyTorch 1.6 及以上版本，因为之前版本的行为不同）。

用户可以使用多线程代码（例如 Hogwild 训练）训练模型，并且不会被并发的反向计算阻塞，示例代码如下：

# 定义一个可在不同线程中使用的训练函数
def train_fn():
    x = torch.ones(5, 5, requires_grad=True)
    # 正向
    y = (x + 3) * (x + 4) * 0.5
    # 反向
    y.sum().backward()
    # 可能的优化器更新

# 用户编写自己的线程代码来驱动 train_fn
threads = []
for _ in range(10):
    p = threading.Thread(target=train_fn, args=())
    p.start()
    threads.append(p)

for p in threads:
    p.join()

需要注意用户应该了解以下行为：

CPU 并发

在 CPU 上通过 Python 或 C++ API 以多线程方式运行 backward() 或 grad() 时，应看到更多的并发执行，而不是按特定顺序将所有反向调用串行化（这是 PyTorch 1.6 之前的行为）。

不确定性

如果您在多线程环境中并发调用 backward() 并共享输入（即 Hogwild CPU 训练），则应预期出现不确定性。这种情况发生的原因在于参数在线程间自动共享，因此多个线程可能会尝试访问并累积相同的 .grad 属性。这在技术上并不安全，可能导致竞争条件，使结果无效。

开发多线程模型并共享参数的用户，应牢记多线程模型并了解上述问题。

可以使用功能性 API torch.autograd.grad() 来计算梯度，以避免不确定性，而非使用 backward()。

保留计算图

如果 autograd 图的一部分在线程之间共享，例如，先在单线程中运行正向传播的第一部分，然后在多线程中运行后续部分，则第一部分图会被共享。在这种情况下，不同的线程在同一个图上执行 grad() 或 backward() 可能会遇到一个线程在执行时销毁图的问题，导致其他线程崩溃。autograd 会向用户报告错误，类似于未设置 retain_graph=True 而多次调用 backward()，并提醒用户应使用 retain_graph=True。

Autograd 节点上的线程安全

由于 Autograd 允许调用线程驱动其反向执行以实现潜在的并行性，因此确保在 CPU 上以并行方式调用 backward() 时线程安全性很重要，特别是共享部分或整个 GraphTask 时。

自定义 Python autograd.Function 自动因 GIL 而线程安全。对于内置的 C++ Autograd 节点（如 AccumulateGrad、CopySlices）和自定义 autograd::Function，Autograd 引擎使用线程互斥锁来确保可能存在状态读/写的 autograd 节点上的线程安全。

C++ 钩子上的线程不安全

Autograd 依赖用户编写线程安全的 C++ 钩子。如果希望钩子在多线程环境中正确应用，需要编写适当的线程锁定代码，确保钩子线程安全。

复数的 Autograd

简要说明：

• 当您使用 PyTorch 对任意复数域和/或复数值域的函数 \(f(z)\) 求导时，梯度是基于该函数作为更大实值损失函数 \(g(\) input \()=L\) 的一部分来计算的。计算的梯度是 \(\frac{\partial L}{\partial z^*}\)（注意 \(z\) 的共轭），其负值正是梯度下降算法中最陡下降的方向。因此，所有现有的优化器都可以直接处理复数参数。

• 这种方式与 TensorFlow 的复数微分惯例相符，但与 JAX 不同（JAX 计算的是 \(\frac{\partial L}{\partial z}\)）。

• 如果有一个实到实的函数，内部使用复数运算，此处的惯例无关紧要：结果将始终与仅使用实数运算的实现相同。

如果您对数学细节感兴趣，或者想知道如何在 PyTorch 中定义复数导数，请继续阅读。

什么是复数导数？

复数可微分的数学定义取导数的极限定义，并将其推广到复数。考虑函数 \(f:\mathbb{C} \rightarrow \mathbb{C}\)，

\[ f(z = x + yj) = u(x, y) + v(x, y)j \]

其中 \(u\) 和 \(v\) 是两个变量的实值函数，\(j\) 是虚数单位。

使用导数定义，我们可以写出：

\[ f^{\prime}(z) = \lim_{h \rightarrow 0, h \in C}\frac{f(z+h) - f(z)}{h} \]

为了使此极限存在，\(u\) 和 \(v\) 不仅必须是实可微的，\(f\) 还必须满足柯西-黎曼方程。换句话说，按实数和虚数步长 \((h)\) 计算的极限必须相等。这是一个更为严格的条件。

复数可微的函数通常被称为全纯函数。它们性质良好，具有实数可微函数的所有优良属性，但在优化领域几乎无用。对于优化问题，研究界通常只使用实值目标函数，因为复数不是有序域的一部分，因此使用复数值损失没有多大意义。

此外，没有有趣的实值目标函数符合柯西-黎曼方程。因此，全纯函数的理论不能用于优化，大多数人转而使用维尔廷格微积分。

维尔廷格微积分登场

我们拥有复数可微性和全纯函数的理论，但由于许多常用函数并非全纯，无法充分利用这一理论。那么数学家 Wirtinger 是怎么做的呢？他发现，即使 \(f(z)\) 不是全纯的，也可以将其重写为双变量函数 \(f(z, z^*)\)，该函数总是全纯的。这是因为 \(z\) 的实部和虚部可以通过 \(z\) 和 \(z^*\) 表示为：

\[ \begin{aligned} \operatorname{Re}(z) = \frac{z + z^*}{2} \\ \operatorname{Im}(z) = \frac{z - z^*}{2j} \end{aligned} \]

维尔廷格微积分建议研究 \(f(z, z^*)\)，如果 \(f\) 实可微，则该函数可保证全纯（另一种看法是这是坐标系的改变，从 \(f(x, y)\) 变为 \(f(z, z^*)\)）。该函数具有偏导数 \(\frac{\partial}{\partial z}\) 和 \(\frac{\partial}{\partial z^*}\)。我们可以使用链式法则建立这些偏导数与 \(z\) 的实部和虚部的偏导数之间的关系：

\[ \begin{aligned} \frac{\partial}{\partial x} = \frac{\partial z}{\partial x} \cdot \frac{\partial}{\partial z} + \frac{\partial z^*}{\partial x} \cdot \frac{\partial}{\partial z^*} \\ \frac{\partial}{\partial y} = \frac{\partial z}{\partial y} \cdot \frac{\partial}{\partial z} + \frac{\partial z^*}{\partial y} \cdot \frac{\partial}{\partial z^*} \end{aligned} \]

从上述方程可得：

\[ \begin{aligned} \frac{\partial}{\partial z} = \frac{1}{2}\left(\frac{\partial}{\partial x} - 1j \cdot \frac{\partial}{\partial y}\right) \\ \frac{\partial}{\partial z^*} = \frac{1}{2}\left(\frac{\partial}{\partial x} + 1j \cdot \frac{\partial}{\partial y}\right) \end{aligned} \]

这就是您在维基百科上找到的维尔廷格微积分的经典定义。

这个改变带来了许多有趣的结果：

• 首先，柯西-黎曼方程简单地翻译成 \(\frac{\partial f}{\partial z^*} = 0\)（即函数 \(f\) 可以完全用 \(z\) 表示，不必涉及 \(z^*\)）。

• 另一个重要（且看似反直觉）的结果是，当我们对实值损失进行优化时，更新变量的步骤由 \(\frac{\partial \text{Loss}}{\partial z^*}\) 决定（而不是 \(\frac{\partial \text{Loss}}{\partial z}\)）。

如需了解更多信息，请查阅：https://arxiv.org/pdf/0906.4835.pdf

维尔廷格微积分在优化中的作用

音频等领域的研究者通常使用梯度下降法，通过复变量来优化实值损失函数。这些研究者通常将实部和虚部分开处理，视为可独立更新的两个通道。对于步长 \(\alpha / 2\) 和损失 \(L\)，我们可以在 \(\mathbb{R}^2\) 中写出以下公式：

\[ \begin{aligned} x_{n+1} & = x_n - (\alpha / 2) \cdot \frac{\partial L}{\partial x} \\ y_{n+1} & = y_n - (\alpha / 2) \cdot \frac{\partial L}{\partial y} \end{aligned} \]

这些公式在复数空间 \(\mathbb{C}\) 中如何转换呢？

\[ \begin{aligned} z_{n+1} & = x_n - (\alpha / 2) \cdot \frac{\partial L}{\partial x} + 1j \cdot \left(y_n - (\alpha / 2) \cdot \frac{\partial L}{\partial y}\right) \\ & = z_n - \alpha \cdot (1 / 2) \cdot \left(\frac{\partial L}{\partial x} + j \frac{\partial L}{\partial y}\right) \\ & = z_n - \alpha \cdot \frac{\partial L}{\partial z^*} \end{aligned} \]

这里发生了一件非常有趣的事情：维尔廷格微积分告诉我们可以将上述复变量更新公式简化，只引用共轭的维尔廷格导数 \(\frac{\partial L}{\partial z^*}\)，这样我们在优化中就可以得到正确的更新步骤。

由于共轭维尔廷格导数能够给出实值损失函数的精确更新步骤，当使用 PyTorch 对具有实值损失的函数求导时，您将获得此导数。

PyTorch 如何计算共轭维尔廷格导数？

通常情况下，我们的导数公式将 grad_output 作为输入，它代表已计算的向量-雅可比积，也即 \(\frac{\partial L}{\partial s^*}\)，其中 \(L\) 是整个计算的损失（产生实值损失），\(s\) 是函数的输出。此处的目标是计算 \(\frac{\partial L}{\partial z^*}\)，其中 \(z\) 是函数的输入。实际上，对于实值损失来说，我们只需计算 \(\frac{\partial L}{\partial s^*}\)，尽管链式法则表明我们还需要获取 \(\frac{\partial L}{\partial s}\)。如果您想跳过此推导，可以直接查看本节的最后一个公式，然后跳到下一节。

继续研究 \(f: \mathbb{C} \to \mathbb{C}\)，定义为 \(f(z) = f(x + yj) = u(x, y) + v(x, y)j\)。如上所述，autograd 的梯度规范围绕实值损失函数的优化，因此假设 \(f\) 是更大实值损失函数 \(g\) 的一部分。使用链式法则，我们可以写出：

\[ \frac{\partial L}{\partial z^*} = \frac{\partial L}{\partial u} \cdot \frac{\partial u}{\partial z^*} + \frac{\partial L}{\partial v} \cdot \frac{\partial v}{\partial z^*} \]

现在使用维尔廷格导数的定义，可以写出：

\[ \begin{aligned} & \frac{\partial L}{\partial s} = \frac{1}{2}\left(\frac{\partial L}{\partial u} - \frac{\partial L}{\partial v}j\right) \\ & \frac{\partial L}{\partial s^*} = \frac{1}{2}\left(\frac{\partial L}{\partial u} + \frac{\partial L}{\partial v}j\right) \end{aligned} \]

需要注意的是，由于 \(u\) 和 \(v\) 是实函数，而假设 \(f\) 是实值函数的一部分，因此 \(L\) 也是实数。我们有：

\[ \left(\frac{\partial L}{\partial s}\right)^* = \frac{\partial L}{\partial s^*} \]

也就是说，\(\frac{\partial L}{\partial s}\) 等于 grad_output 的共轭。

解出上述关于 \(\frac{\partial L}{\partial u}\) 和 \(\frac{\partial L}{\partial v}\) 的方程，我们得到：

\[ \begin{aligned} \frac{\partial L}{\partial u} = \frac{\partial L}{\partial s} + \frac{\partial L}{\partial s^*} \\ \frac{\partial L}{\partial v} = -1j \cdot \left(\frac{\partial L}{\partial s} - \frac{\partial L}{\partial s^*}\right) \end{aligned} \]

将公式 (3) 代入 (1)，得到：

\[ \begin{aligned} \frac{\partial L}{\partial z^*} & = \left(\frac{\partial L}{\partial s} + \frac{\partial L}{\partial s^*}\right) \cdot \frac{\partial u}{\partial z^*} - 1j \cdot \left(\frac{\partial L}{\partial s} - \frac{\partial L}{\partial s^*}\right) \cdot \frac{\partial v}{\partial z^*} \\ & = \frac{\partial L}{\partial s} \cdot \left(\frac{\partial u}{\partial z^*} + \frac{\partial v}{\partial z^*}j\right) + \frac{\partial L}{\partial s^*} \cdot \left(\frac{\partial u}{\partial z^*} - \frac{\partial v}{\partial z^*}j\right) \\ & = \frac{\partial L}{\partial s^*} \cdot \frac{\partial (u + vj)}{\partial z^*} + \frac{\partial L}{\partial s} \cdot \frac{\partial (u + vj)^*}{\partial z^*} \\ & = \frac{\partial L}{\partial s} \cdot \frac{\partial s}{\partial z^*} + \frac{\partial L}{\partial s^*} \cdot \frac{\partial s^*}{\partial z^*} \end{aligned} \]

根据公式 (2)，我们得到：

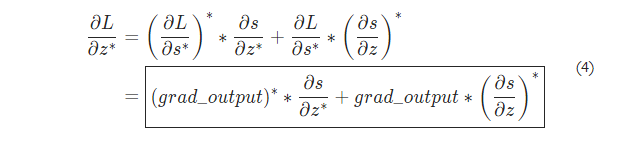
最后一个公式非常重要，它将我们的导数公式分解为一个更简单、易于手动计算的形式。

如何为复数函数编写导数公式？

上面框中的方程为复数函数的所有导数提供了通用公式，但我们仍需计算 \(\frac{\partial s}{\partial z}\) 和 \(\frac{\partial s}{\partial z^*}\)。以下是两种方法：

• 第一种方法是直接使用维尔廷格导数的定义，通过 \(\frac{\partial s}{\partial x}\) 和 \(\frac{\partial s}{\partial y}\)（可以以常规方式计算）计算 \(\frac{\partial s}{\partial z}\) 和 \(\frac{\partial s}{\partial z^*}\)。

• 第二种方法是使用变量替换，将 \(f(z)\) 重写为双变量函数 \(f(z, z^*)\)，通过将 \(z\) 和 \(z^*\) 视为独立变量来计算共轭维尔廷格导数。这通常更容易；例如，如果函数全纯，则只使用 \(z\)（且 \(\frac{\partial s}{\partial z^*}\) 为零）。

让我们以函数 \(f(z = x + yj) = c \cdot z = c \cdot (x + yj)\) 为例，其中 \(c \in \mathbb{R}\)。

使用第一种方法计算维尔廷格导数：

\[ \begin{aligned} \frac{\partial s}{\partial z} & = \frac{1}{2}\left(\frac{\partial s}{\partial x} - \frac{\partial s}{\partial y}j\right) \\ & = \frac{1}{2}(c - (c \cdot 1j) \cdot 1j) \\ & = c \end{aligned} \]

\[ \begin{aligned} \frac{\partial s}{\partial z^*} & = \frac{1}{2}\left(\frac{\partial s}{\partial x} + \frac{\partial s}{\partial y}j\right) \\ & = \frac{1}{2}(c + (c \cdot 1j) \cdot 1j) \\ & = 0 \end{aligned} \]

根据公式 (4) 并设 grad_output = 1.0（这是在 PyTorch 中对标量输出调用 backward() 时的默认梯度输出值），我们得到：

\[ \frac{\partial L}{\partial z^*} = 1 \cdot 0 + 1 \cdot c = c \]

使用第二种方法计算维尔廷格导数，可以直接得到：

\[ \begin{aligned} \frac{\partial s}{\partial z} & = \frac{\partial (c \cdot z)}{\partial z} \\ & = c \\ \frac{\partial s}{\partial z^*} & = \frac{\partial (c \cdot z)}{\partial z^*} \\ & = 0 \end{aligned} \]

再次使用公式 (4)，我们得到 \(\frac{\partial L}{\partial z^*} = c\)。由此可见，第二种方法计算更少，更方便于快速计算。

跨域函数呢？

有些函数从复数输入映射到实数输出，或反之亦然。这些函数是公式 (4) 的特殊情况，可以通过链式法则推导：

• 对于 \(f: \mathbb{C} \to \mathbb{R}\)，我们得到：

\[ \frac{\partial L}{\partial z^*} = 2 \cdot \text{grad\_output} \cdot \frac{\partial s}{\partial z^*} \]

• 对于 \(f: \mathbb{R} \to \mathbb{C}\)，我们得到：

\[ \frac{\partial L}{\partial z^*} = 2 \cdot \operatorname{Re}\left(\text{grad\_output}^* \cdot \frac{\partial s}{\partial z^*}\right) \]

已保存张量的钩子

可以通过定义 pack_hook / unpack_hook 钩子对来控制已保存张量的打包/解包方式。pack_hook 函数应以张量作为唯一参数，但可以返回任何 Python 对象（例如另一个张量、元组，甚至包含文件名的字符串）。unpack_hook 函数的唯一参数是 pack_hook 的输出，并应返回用于反向传播的张量。unpack_hook 返回的张量只需与传递给 pack_hook 的张量内容相同，特别是任何与 autograd 相关的元数据都可以忽略，因为它们会在解包过程中被覆盖。

这对钩子的一个示例是：

x = torch.randn(5, requires_grad=True)
y = x.pow(2)
y.grad_fn._raw_saved_self.register_hooks(pack_hook, unpack_hook)

在注册成对的钩子时立即调用 pack_hook 方法，而每次需要访问保存的张量时（通过 y.grad_fn._saved_self 或在反向传播期间），都会调用 unpack_hook 方法。

警告

如果在保存的张量已被释放（即反向传播调用后）仍保留对 SavedTensor 的引用，则禁止调用其 register_hooks()。PyTorch 通常会抛出错误，但在某些情况下可能不会抛错，并可能出现未定义行为。

# 仅将大小 >= 1000 的张量保存在磁盘上
SAVE_ON_DISK_THRESHOLD = 1000

def pack_hook(x):
    if x.numel() < SAVE_ON_DISK_THRESHOLD:
        return x
    temp_file = SelfDeletingTempFile()
    torch.save(tensor, temp_file.name)
    return temp_file

def unpack_hook(tensor_or_sctf):
    if isinstance(tensor_or_sctf, torch.Tensor):
        return tensor_or_sctf
    return torch.load(tensor_or_sctf.name)

class Model(nn.Module):
    def forward(self, x):
        with torch.autograd.graph.saved_tensors_hooks(pack_hook, unpack_hook):
            # 计算输出
            output = x
        return output

model = Model()
net = nn.DataParallel(model)

使用该上下文管理器定义的钩子是线程局部的。因此，以下代码不会产生预期的效果，因为钩子无法通过 DataParallel：

# 示例：不要这样做

net = nn.DataParallel(model)
with torch.autograd.graph.saved_tensors_hooks(pack_hook, unpack_hook):
    output = net(input)

请注意，使用这些钩子会禁用为减少 Tensor 对象创建而进行的优化。例如：

with torch.autograd.graph.saved_tensors_hooks(lambda x: x, lambda x: x):
    x = torch.randn(5, requires_grad=True)
    y = x * x

在没有钩子的情况下，x、y.grad_fn._saved_self 和 y.grad_fn._saved_other 都引用同一个张量对象。但有钩子时，PyTorch 会将 x 打包和解包成两个新的张量对象，它们与原始的 x 共享相同的存储（不会执行复制操作）。

反向传播钩子的执行

本节将讨论何时触发不同的钩子，何时不会触发，然后讨论触发顺序。涵盖的钩子有：通过 torch.Tensor.register_hook() 注册到张量的反向钩子，通过 torch.Tensor.register_post_accumulate_grad_hook() 注册到张量的梯度累积后钩子，通过 torch.autograd.graph.Node.register_hook() 注册到节点的后钩子，以及通过 torch.autograd.graph.Node.register_prehook() 注册到节点的前钩子。

钩子是否会触发

通过 torch.Tensor.register_hook() 注册到张量的钩子，会在为该张量计算梯度时执行（注意，这不要求执行该张量的 grad_fn。例如，如果该张量作为 torch.autograd.grad() 的 inputs 参数的一部分传递，可能不会执行张量的 grad_fn，但该张量的钩子始终会被执行）。

通过 torch.Tensor.register_post_accumulate_grad_hook() 注册到张量的钩子，在该张量的梯度累积之后执行，这意味着该张量的 grad 字段已经设置。通过 torch.Tensor.register_hook() 注册的钩子在计算梯度时执行，而通过 torch.Tensor.register_post_accumulate_grad_hook() 注册的钩子只会在反向传播结束时，autograd 更新张量的 grad 字段后触发。因此，梯度累积后钩子只能为叶张量注册。如果尝试在非叶张量上注册，会抛出错误，即使 backward(retain_graph=True) 被调用也是如此。

通过 torch.autograd.graph.Node.register_hook() 或 torch.autograd.graph.Node.register_prehook() 注册到 torch.autograd.graph.Node 的钩子，只有在节点执行时才会触发。

特定节点是否执行取决于反向传播是否通过 torch.autograd.grad() 或 torch.autograd.backward() 调用。特别是，如果您在对应于传递给 inputs 参数的张量的节点上注册钩子，应了解这两者之间的差异。

如果使用 torch.autograd.backward()，上述所有钩子都会执行，无论是否指定了 inputs 参数。这是因为 .backward() 会执行所有节点，即使它们对应于作为输入指定的张量。（注意，执行额外的节点通常是不必要的，但仍会这样做。这种行为可能会发生变化，因此不应依赖它。）

另一方面，如果使用 torch.autograd.grad()，传递给 input 的张量所对应节点上的反向钩子可能不会执行，因为除非有另一个输入依赖于该节点的梯度结果，否则不会执行这些节点。

钩子触发顺序

执行顺序如下：

1. 钩子注册到张量时执行
2. 钩子注册到节点的前钩子时执行（如果节点执行）
3. 为保留梯度的张量更新 .grad 字段
4. 节点执行（受上述规则约束）
5. 梯度累积的叶张量执行梯度累积后钩子
6. 钩子注册到节点的后钩子时执行（如果节点执行）

如果同类型的多个钩子注册到同一个张量或节点，将按注册顺序执行。后执行的钩子可以看到之前钩子对梯度的修改。

特殊钩子

torch.autograd.graph.register_multi_grad_hook() 是使用注册到张量的钩子实现的。每个单独的张量钩子按照上述顺序执行，已注册的多重梯度钩子会在计算最后一个张量的梯度时触发。

torch.nn.modules.module.register_module_full_backward_hook() 是使用注册到节点的钩子实现的。计算正向传播时，钩子会注册到模块的输入和输出的 grad_fn。由于模块可能有多个输入并返回多个输出，因此自定义的 autograd 函数首先应用于模块的输入，再应用于模块的输出，以确保这些张量共享一个 grad_fn，从而可以将钩子附加到其中。

修改张量时的钩子行为

通常，注册到张量的钩子会接收相对于该张量的输出梯度，此时张量的值是执行反向传播时的值。

但是，如果您在注册钩子后修改张量，修改前注册的钩子也会接收相对于该张量的输出梯度，但此时张量的值是修改前的值。

如果更喜欢前一种情况的行为，应在修改张量后再注册钩子。例如：

t = torch.tensor(1., requires_grad=True).sin()
t.cos_()
t.register_hook(fn)
t.backward()

此外，需要知道注册到张量的钩子实际上永久绑定到该张量的 grad_fn 上。因此，如果修改张量，即使该张量现在有一个新的 grad_fn，修改前注册的钩子仍会与旧的 grad_fn 关联。例如，当 autograd 引擎在计算图中达到该张量的旧 grad_fn 时，它们将会触发。

Tensor.register_hook(hook)

注册一个反向传播钩子。

每次计算该张量的梯度时都会调用该钩子。钩子的签名应如下：

hook(grad) -> Tensor or None

钩子不应修改其参数，但可以选择性地返回一个新的梯度，用以替换原来的 grad。

该函数返回一个句柄，具有 handle.remove() 方法，可以用来将钩子从模块中移除。

注意

有关此钩子何时执行以及其与其他钩子的执行顺序，请参阅反向传播钩子的执行。

示例：

v = torch.tensor([0., 0., 0.], requires_grad=True)
h = v.register_hook(lambda grad: grad * 2)  # 将梯度翻倍
v.backward(torch.tensor([1., 2., 3.]))
v.grad
# 输出：
# tensor([2., 4., 6.])

h.remove()  # 移除钩子