PyTorch Autograd Explained In depth Tutorial

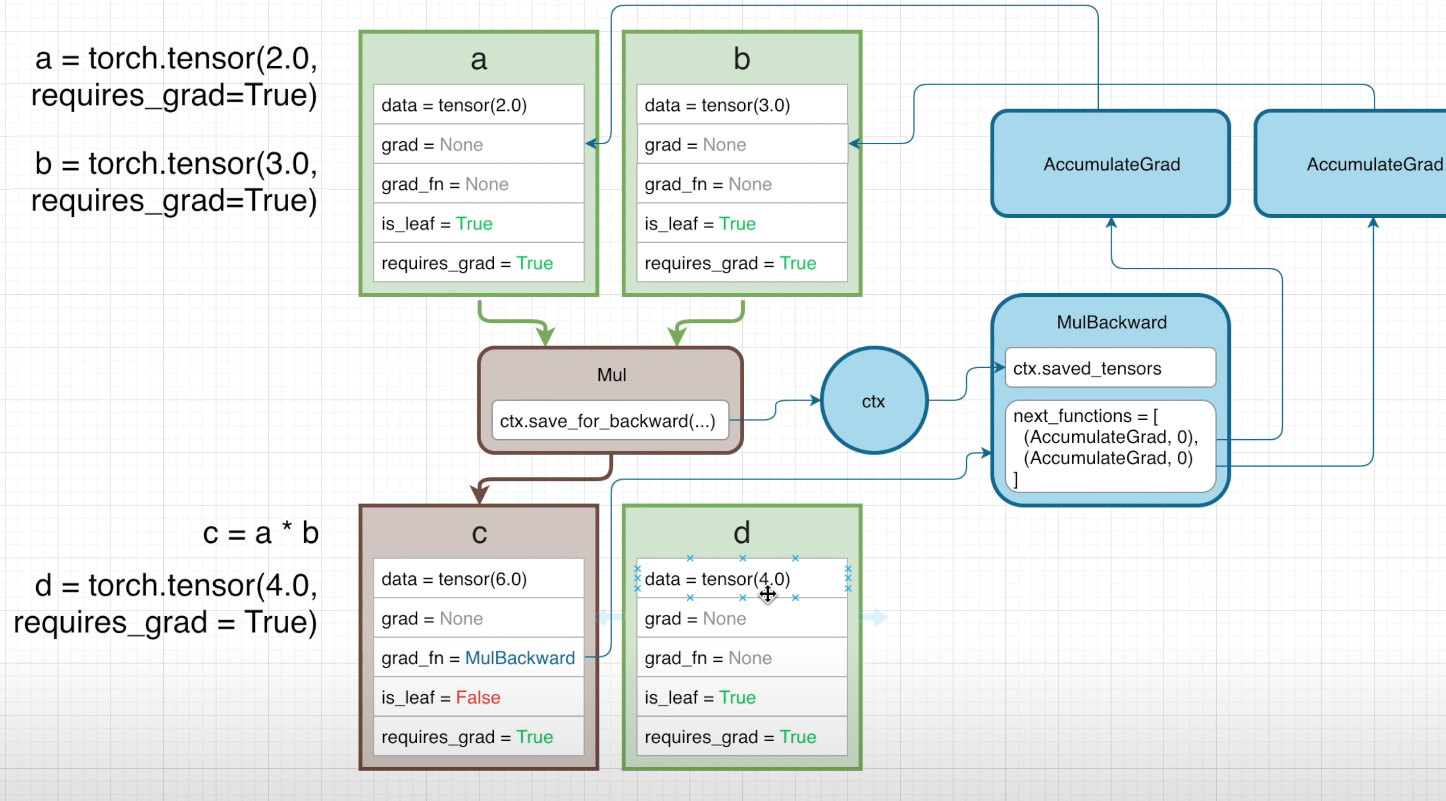
首先我们定义两个张量，其中框中的是它们的属性

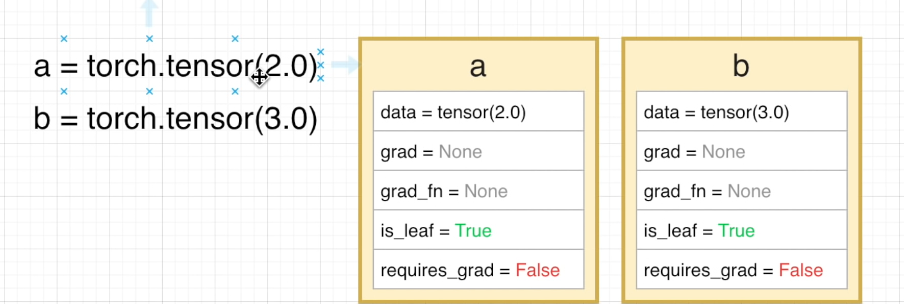
可以看到，这里面 a 和 b 两个张量的 grad 以及 grad_fn 属性都是 None 这表明，这两个张量目前没有梯度值以及装备的用于的求梯度的函数（这里借用了装备范数的说法，不太严谨，意会即可）

is_leaf 属性说明了这两个张量目前是计算图中的一个叶子，requires_grad = False 则说明这两个张量不需要求梯度，接下来我们定义了一个函数，这里就简单定义为 Mul （Multiple）

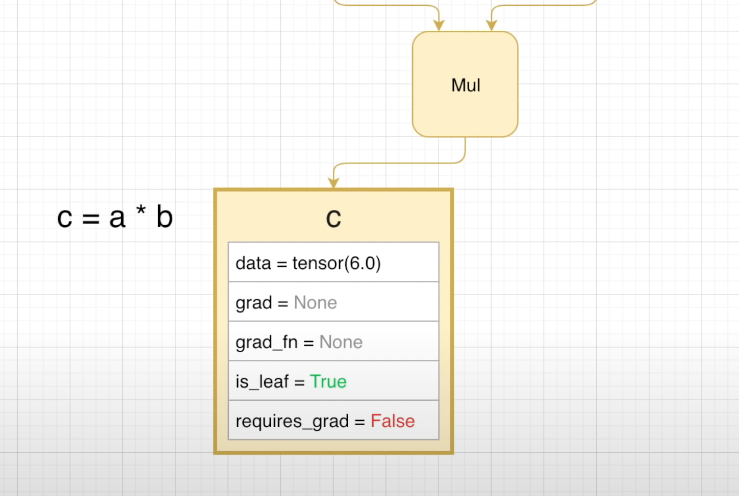
可以看到，在进行了一次计算后，得到的新张量 c 同样具有和 a 以及 b 相似的属性，没有梯度值，没有装备求梯度的函数，仍然是计算图中的叶子，同样是 requires_grad = False

因此在这一次操作中，不会生成反向传播的计算图

接下来我们将张量 a 设置为 requires_grad = True

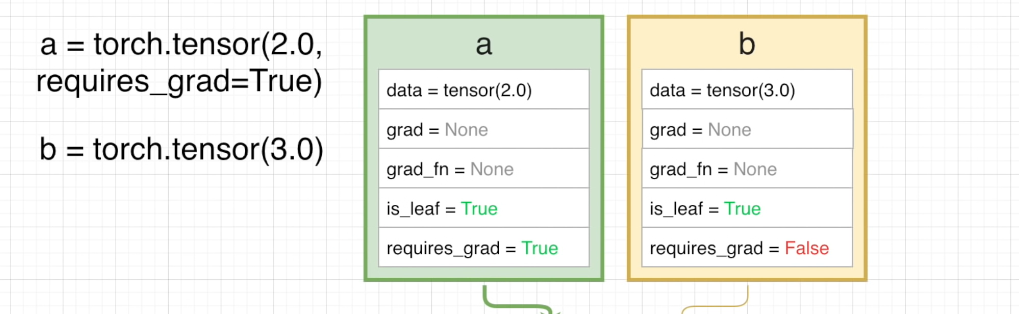
这次我们得到的张量 c 就不再是计算图的一部分了，出于 a 的属性，c 现在是反向传播计算图中的一个节点

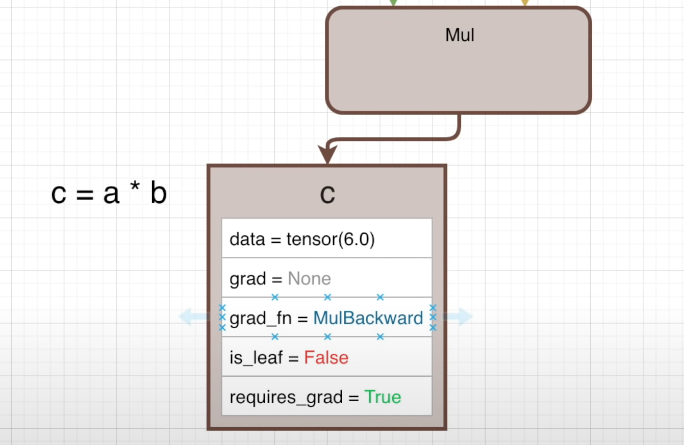
可以看到，这里 c 自动装备了用于计算梯度的函数 MulBackward，is_leaf 属性变为 False

事实上，同时也生成了反向传播的计算图

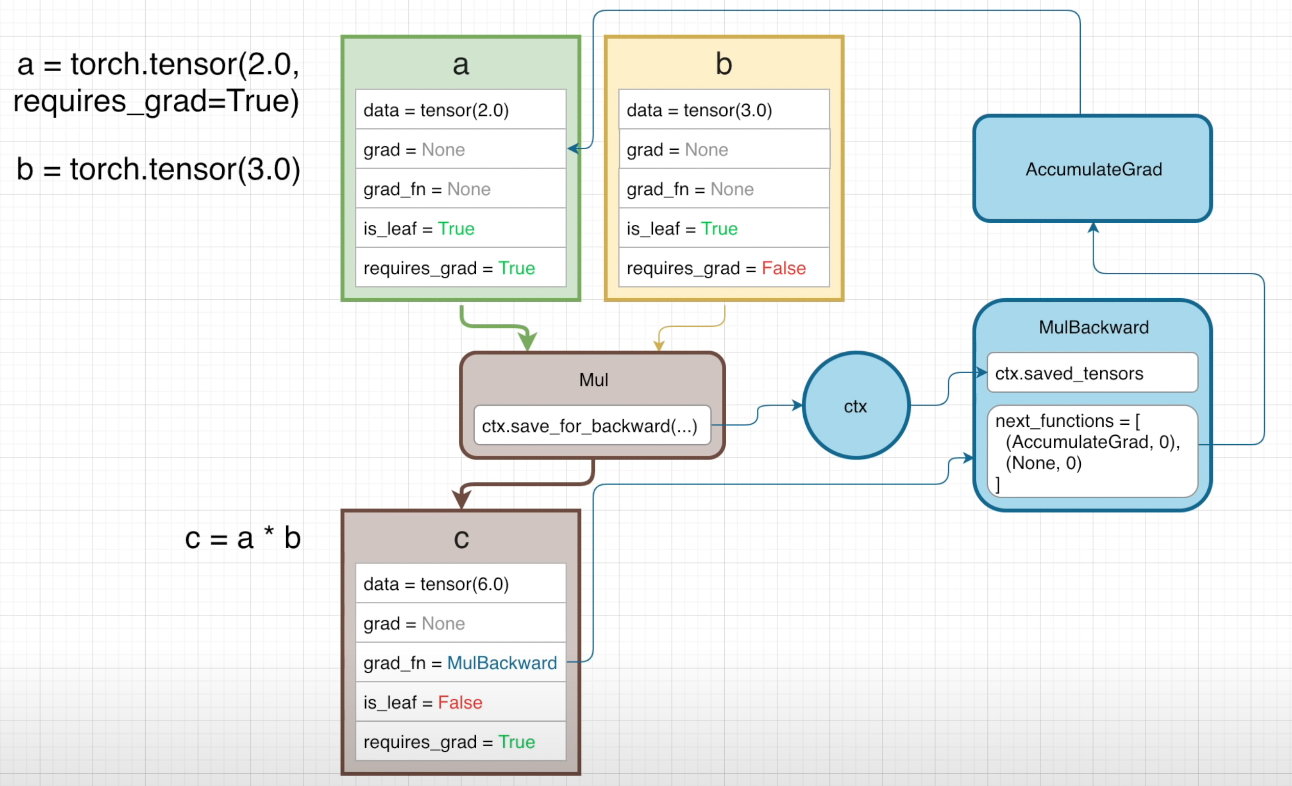
当我们对一个操作函数（这里是 Mul）传入一个 requires_grad = True 的变量时，它会自动调用背景变量 context variable 来储存反向传播所需要的值并将它们传入用于计算梯度的函数（或者说，用于反向传播的）中

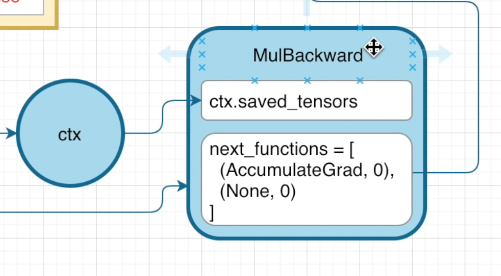
当然，这里只是做原理讲解，实际上这么做是不安全的，pytorch 会使用更加符号化的方法调用这些方法

在 MulBackward 的属性中，next_functions 是一个元组，它储存了将要通过这个函数的不同输入，例如在上面的例子中，AccumulateGrad 指的是张量 a（对应于其属性），None 指的则是张量 b，这样做的意义是：在进行求梯度操作时，我们可以只输入那些需要求梯度的张量

在经过一整轮计算后，计算图则如下图所示

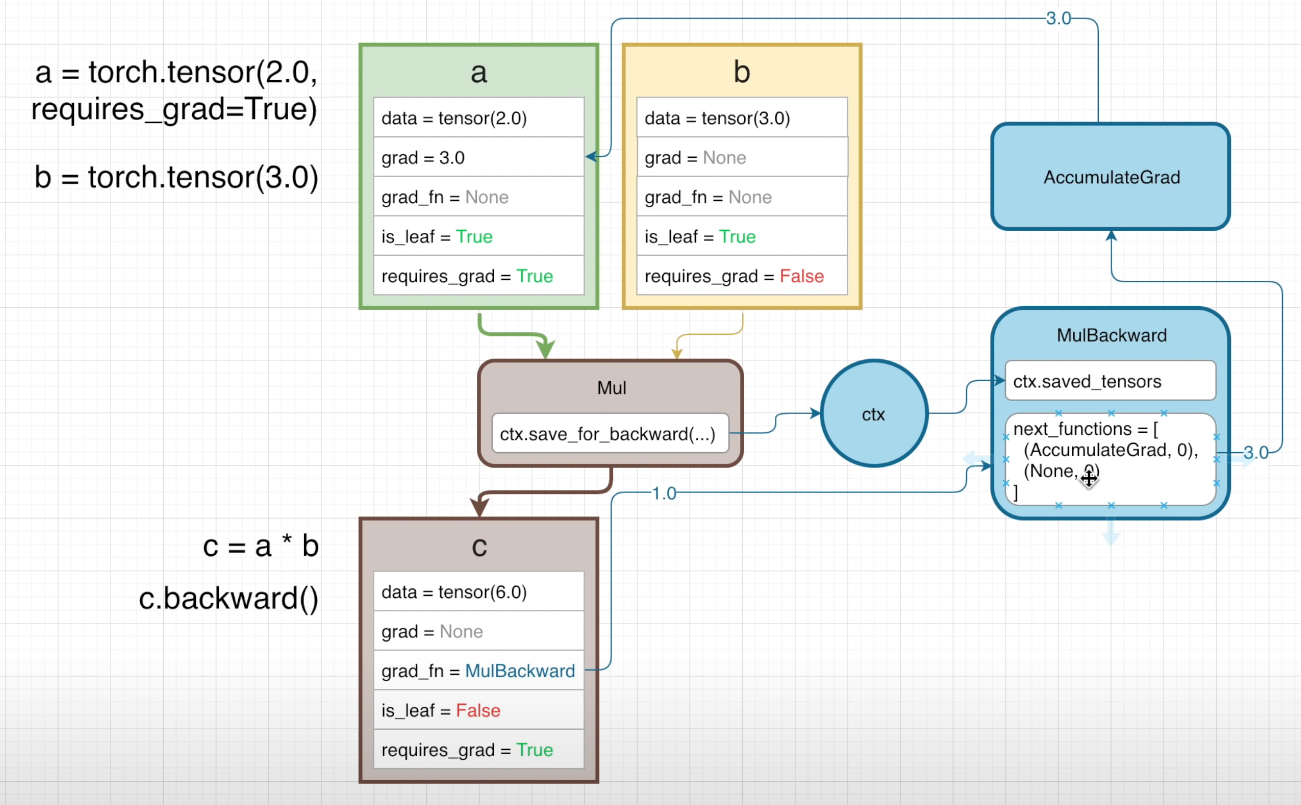
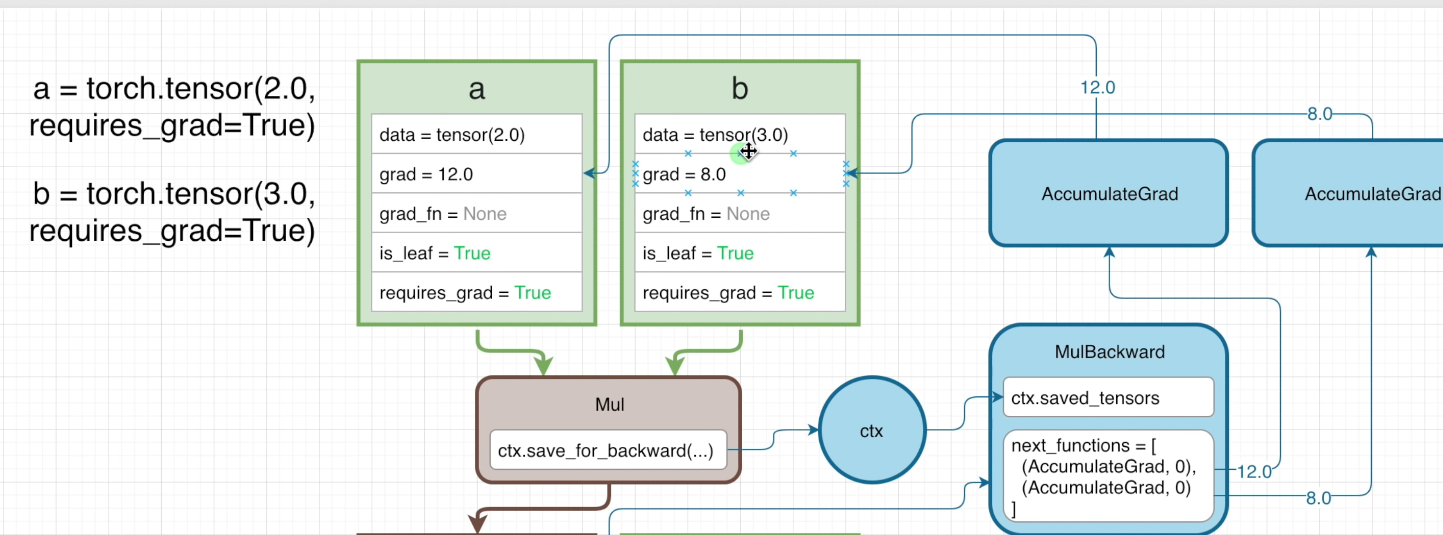
可以看到，在反向传播的过程中，梯度值首先会被初始化为 1 ，接着进入反向传播函数中，在这个情况下，梯度值会被计算为 3（因为这里相当于传入了一个函数 3*a 其中 a = 2 )，最后返回时就会发现这里 a 的属性发生了变化，而 b 因为没有传入反向传播函数中，梯度值仍然是 None

那么在 b 的 requires_grad = True 的情况下呢，又会变成什么样子？

并且我们同样创建一个属性类似的张量 d ，与 c 进行 Mul 操作

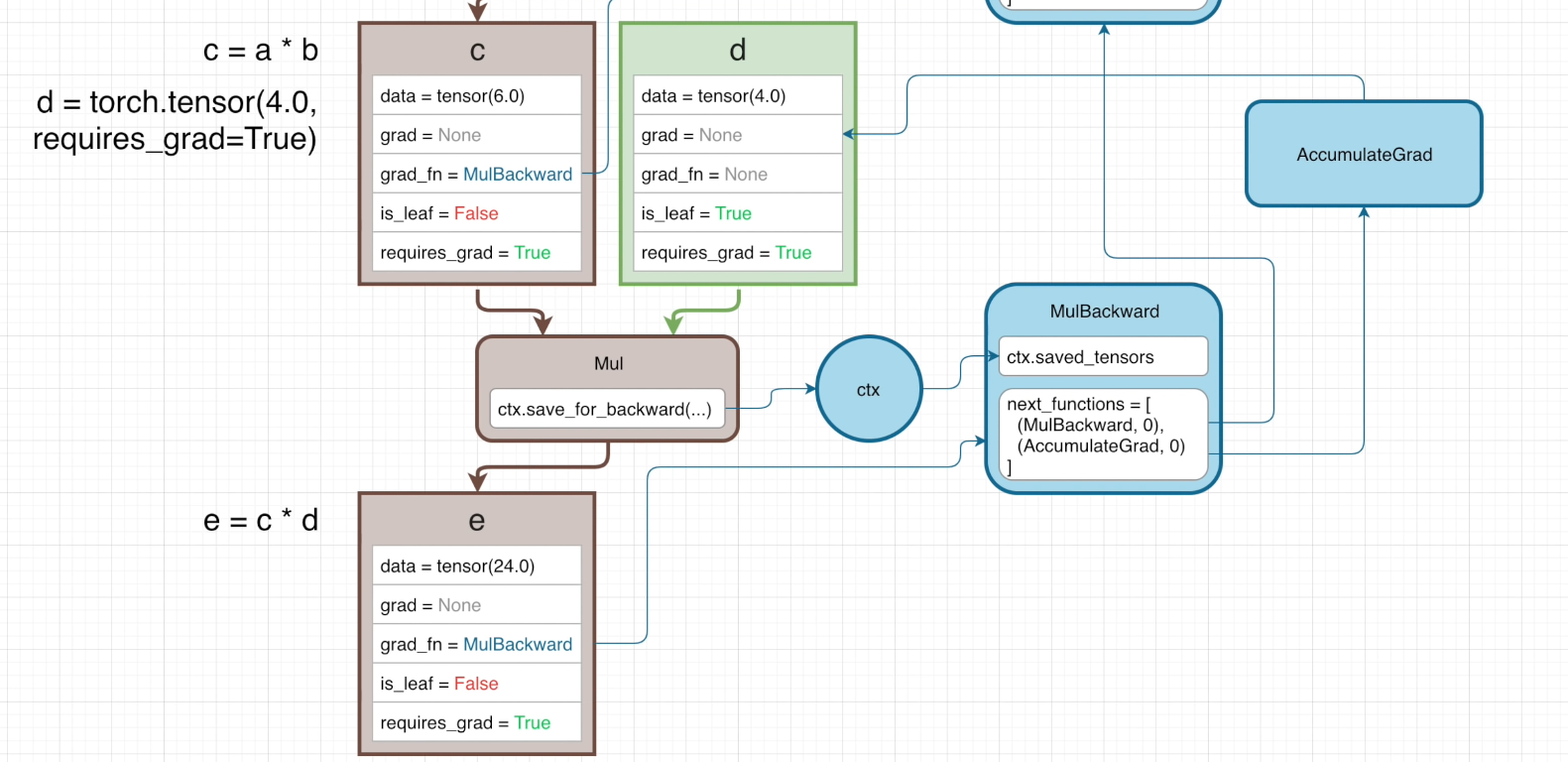
但在这里我们看到了一个特殊的问题，在第二个 MulBackward 的属性列表中，第一个元素仍然是 MulBackward ，这是因为 c 并不是计算图的一部分，它是一个 intermediate node（位于多个分支末端的节点），因此我们不需要计算它的梯度。在计算整体梯度时，我们只需要传入与 c 这个张量有关的函数的反向传播函数（即 c*d）

在对这个前向传播进行反向传播时，同样我们先将梯度值初始化为 1，接着进入第一个 MulBackward ，这里面因为第二个 Mul 对 c 来说是 4*c 因此这里返回的第一个梯度是 4，同样 d 返回的梯度是 6；对于 d 而言，这个梯度 6 同时也会从 AccumulateGrad 函数中返回，储存在 grad 属性中

接着通过链式法则，我们然后得到了相对于 a 和 b 的梯度（a → c → e 以及 b→ c → e，因此一个是 3*4 另一个是 2*4）

如何保证变量（在这里是 c）不会随着前向传播改变值？如果我们在前向传播的过程中设置如下代码

e = c * d
c += ·

反向传播是否会传播出现问题？事实上，在进行前向传播时，会有一个参数用于记录变量目前的“版本”

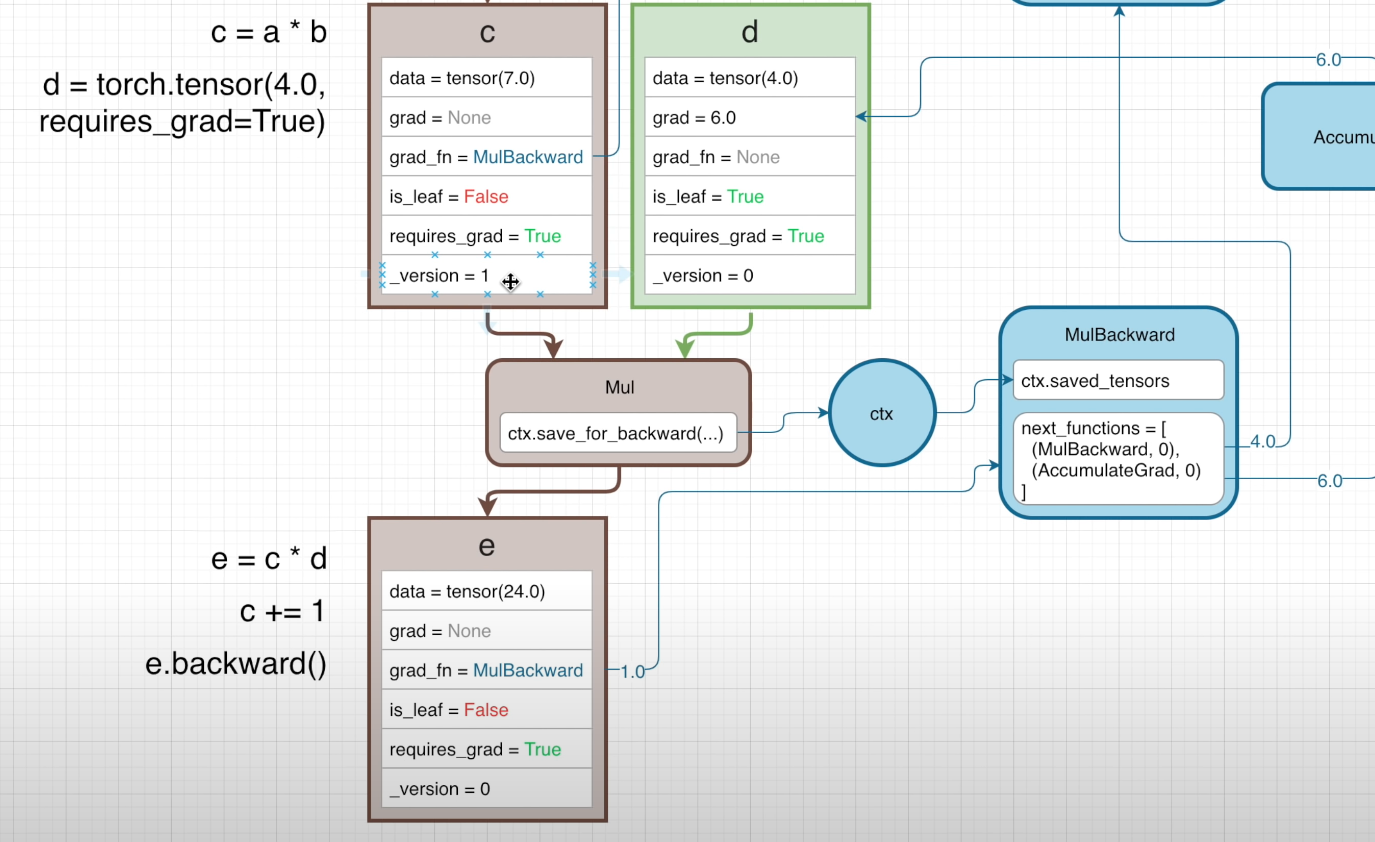
变量被初始化时，_version 的值是 0 ，而每进行一次操作，_version 的值就会增加 1，在 c 进入 Mul 前，它的 _version = 0 因此反向传播调用的是这个版本的 c

接着来看一维向量

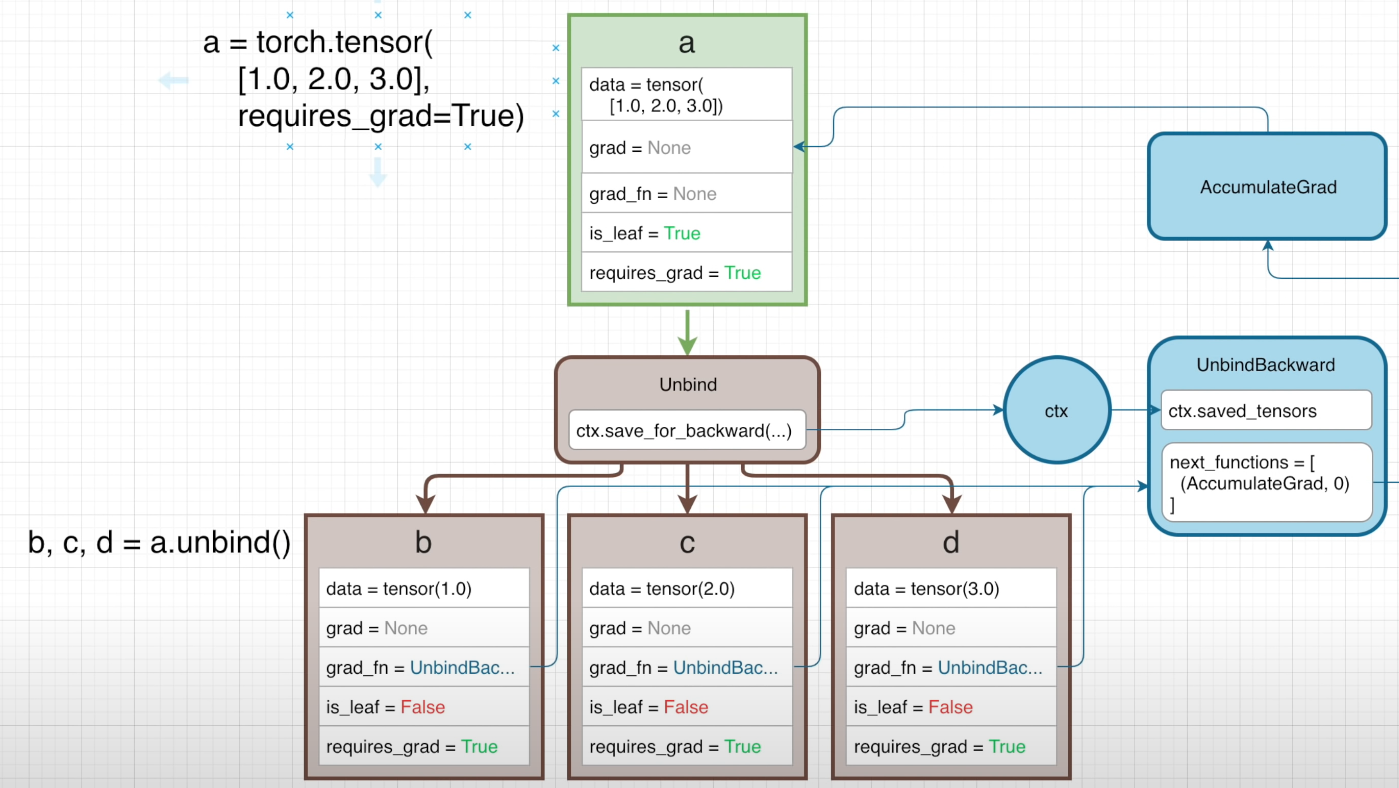
首先定义了一个一维张量 a ，接着进行解包操作，将其拆分为 b,c,d 三个张量，可以看到在反向传播计算图中调用的是 UnbindBackward 函数

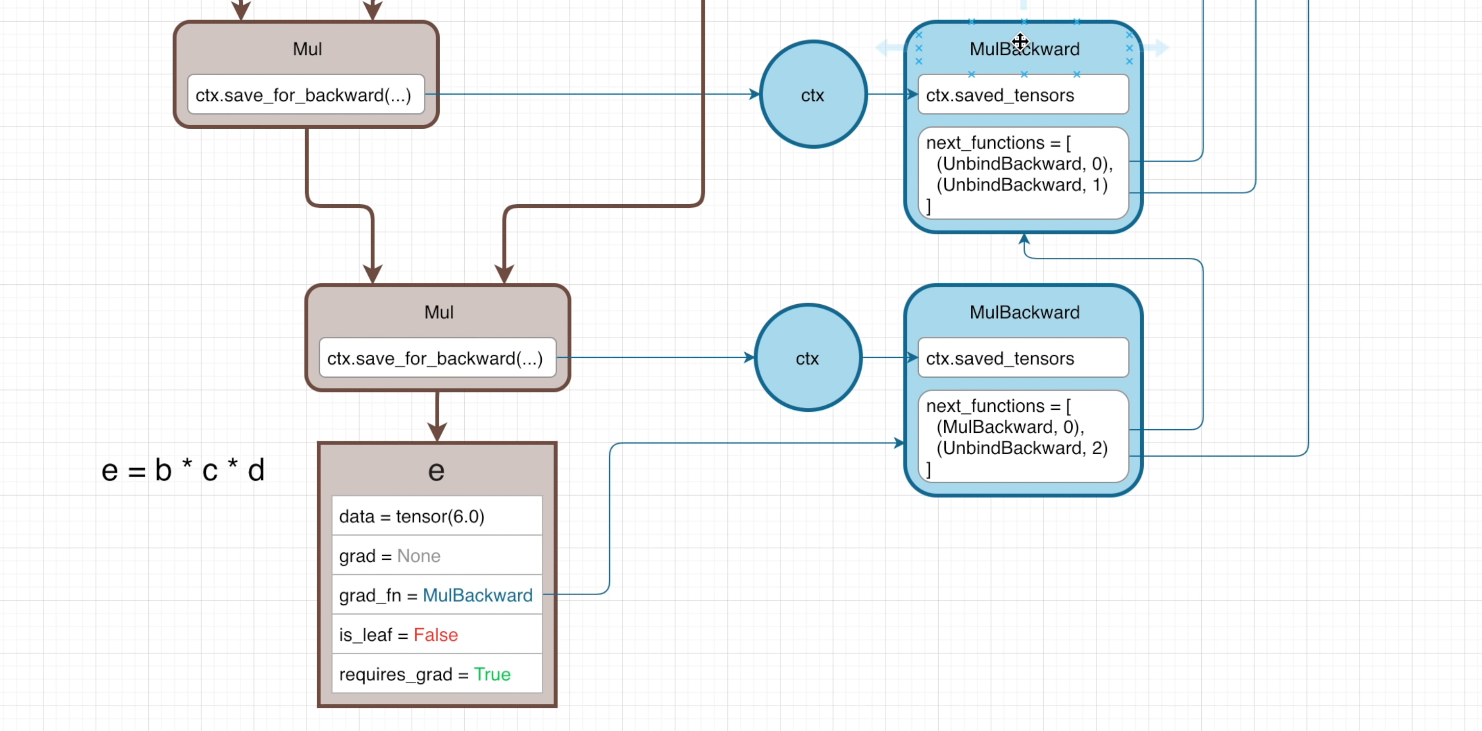
在接下来的前向传播中定义了两个乘法操作：b*c 以及用 d 乘以 b*c 的结果得到 e 即 b*c*d=e

在反向传播的参数中，我们可以看到 UnbindBackward 分别具有参数 0,1,2 ——这是分别是指 a 经过 Unbind 操作之后生成的 b,c,d 的反向传播函数

换句话说，下方的框中表现出了这样的函数关系：输入相乘结果 Mul(b,d) 以及另一个输入 d 求梯度

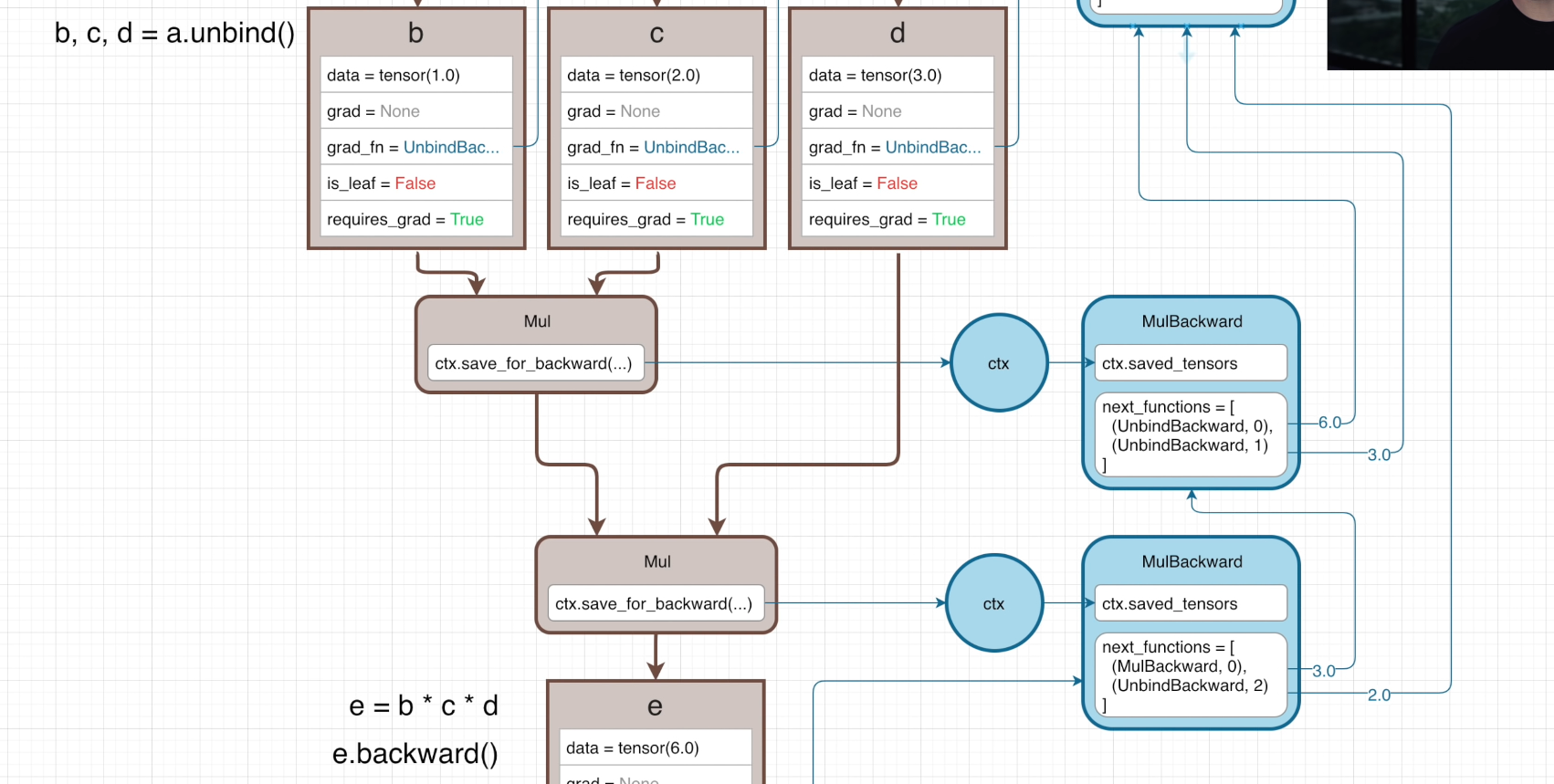
在这次的反向传播中，仍然遵循之前的法则，对于 Mul 来说，其梯度就是 d = 3 ，同理对 d 的梯度是 2

对于 d 来说，它在计算中仅有这一次调用，因此直接返回 AccumulateGrad 中，而对于第一个 Mul 它的梯度则分别是 2 和 1，因此根据链式法则返回 6 和 3

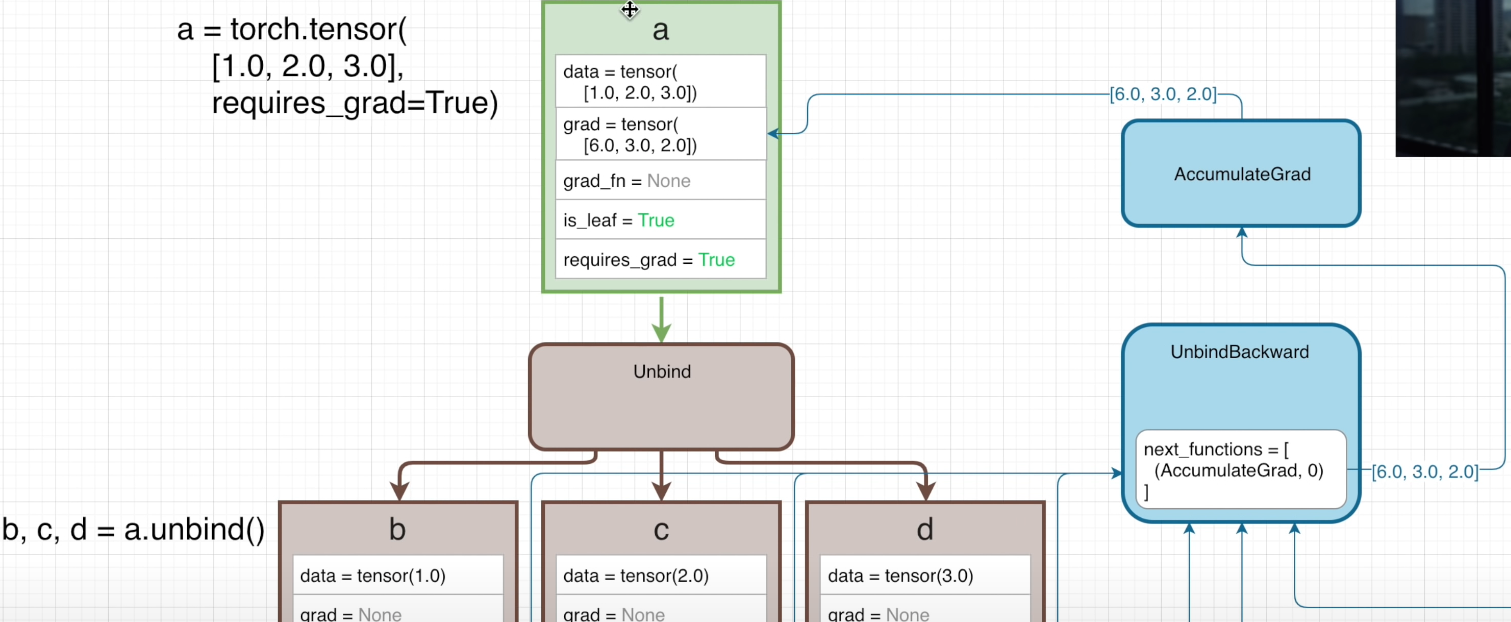
然后我们看一下另一种情况，a 和 b 都不需要求梯度，但是 c 需要求梯度

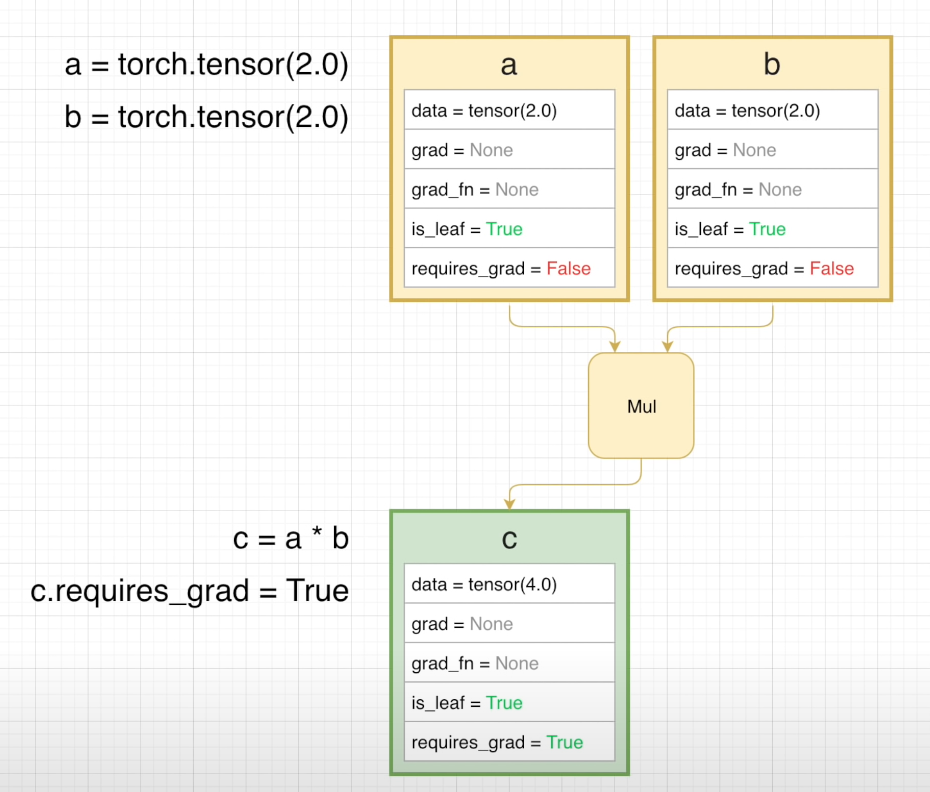
同时我们创建一个不需要求梯度的张量 d ，和之前一样

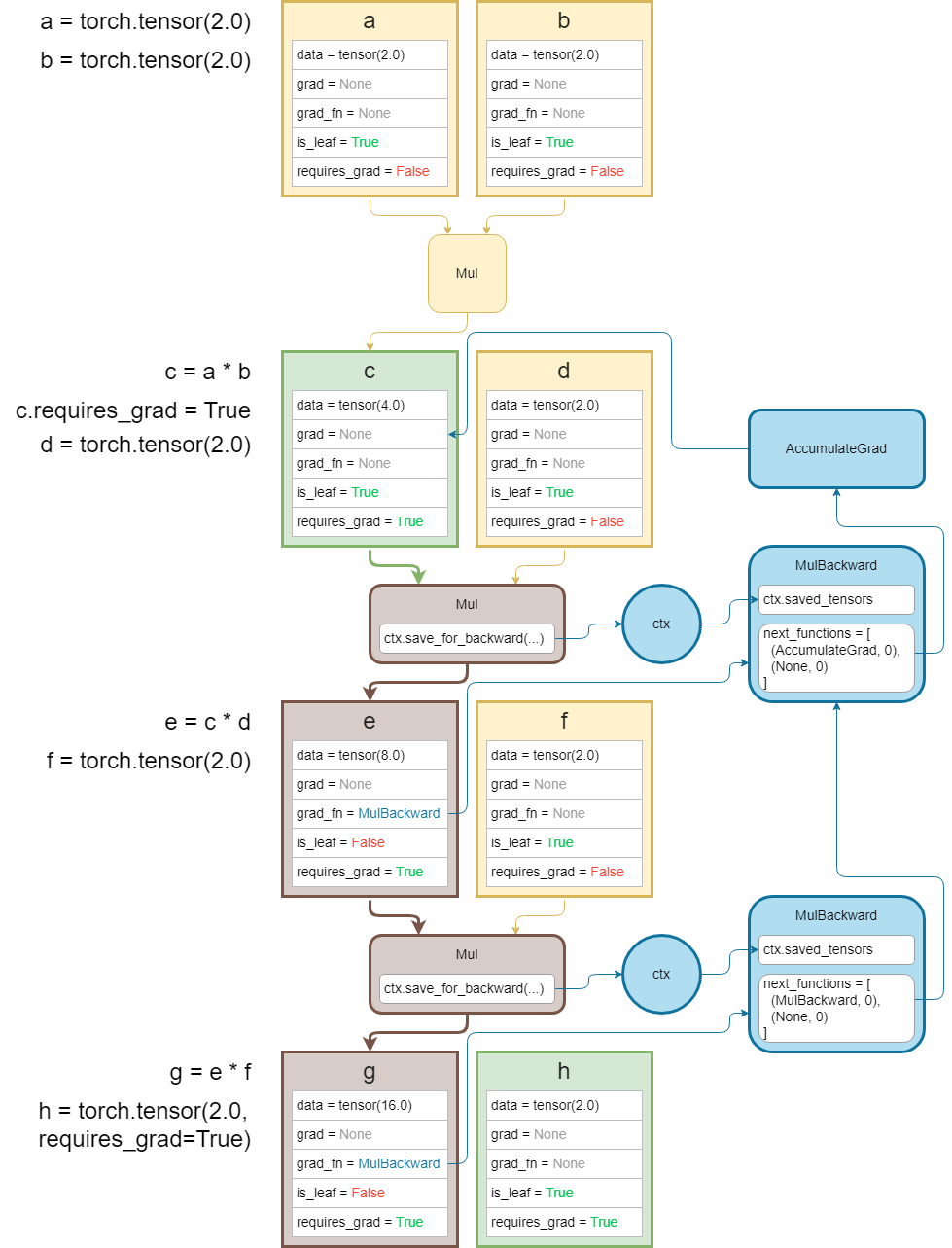
一个稍显复杂的前向传播过程以及与上面类似的反向传播