RNA velocity of single cells

摘要¶

RNA 的丰度是反映单个细胞状态的强有力指标。单细胞 RNA 测序能够高精度、高敏感性及高通量地揭示 RNA 的丰度。然而，这种方法只能捕获某一时间点的静态快照，这对于分析如胚胎发育或组织再生等时间解析现象构成挑战。我们在这里展示，通过在常见的单细胞 RNA 测序协议中区分未剪接和已剪接的 mRNA，可以直接估计 RNA 速度——基因表达状态的时间导数。 RNA 速度是一个高维向量，能预测单个细胞在几小时内的未来状态。我们在神经嵴谱系中验证了其准确性，演示了其在多个已发布数据集和技术平台上的应用，揭示了发育中的小鼠海马的分支谱系树，并检查了人类胚胎大脑的转录动力学。我们期望 RNA 速度将大大促进发育谱系和细胞动态的分析，特别是在人类中。

正文¶

在发育过程中，细胞分化通常发生在几小时到几天的时间尺度上，这与 mRNA 的典型半衰期相当。通过利用新生（未剪接）与成熟（已剪接）mRNA 的相对丰度，可以估计基因剪接和降解的速率，无需像以往在整体实验中使用代谢标记那样 2,3,4。我们推测，在单细胞 RNA 测序（RNA-seq）数据中可能检测到类似的信号，这些信号可能揭示了在动态过程中整个转录组变化的速率和方向。

所有常见的单细胞 RNA-seq 协议都依赖于寡聚 dT 引物来富集带有聚腺苷酸的 mRNA 分子。尽管如此，在基于 SMART-seq2、STRT/C1、inDrop 以及 10x Genomics Chromium 协议 5,6,7,8 的单细胞 RNA-seq 数据集分析中，我们发现 15-25% 的读段包含未剪接的内含子序列（图 1a），这与之前在整体 4（14.6%）和单细胞 5（约 20%）RNA-seq 中的观察结果一致。大多数此类读段源于内含子区域内的次级引物结合位点（扩展数据图 1）。在 10x Genomics Chromium 库中，我们还发现了来自更常见的内含子 -polyT 序列的大量不一致引物（扩展数据图 1），这可能在 PCR 扩增过程中通过一链 cDNA 上的引物生成。大量的内含子分子及其与外显子计数的相关性表明这些分子代表了未剪接的前体 mRNA。通过对新转录的 RNA 进行代谢标记，随后使用寡聚 dT 引物的单细胞标记逆转录（STRT）10 进行 RNA 测序（扩展数据图 2）证实了这一点；83% 的所有基因显示的表达时间进程与预期的简单一级动力学一致，如未剪接读段代表新生 mRNA 所示。

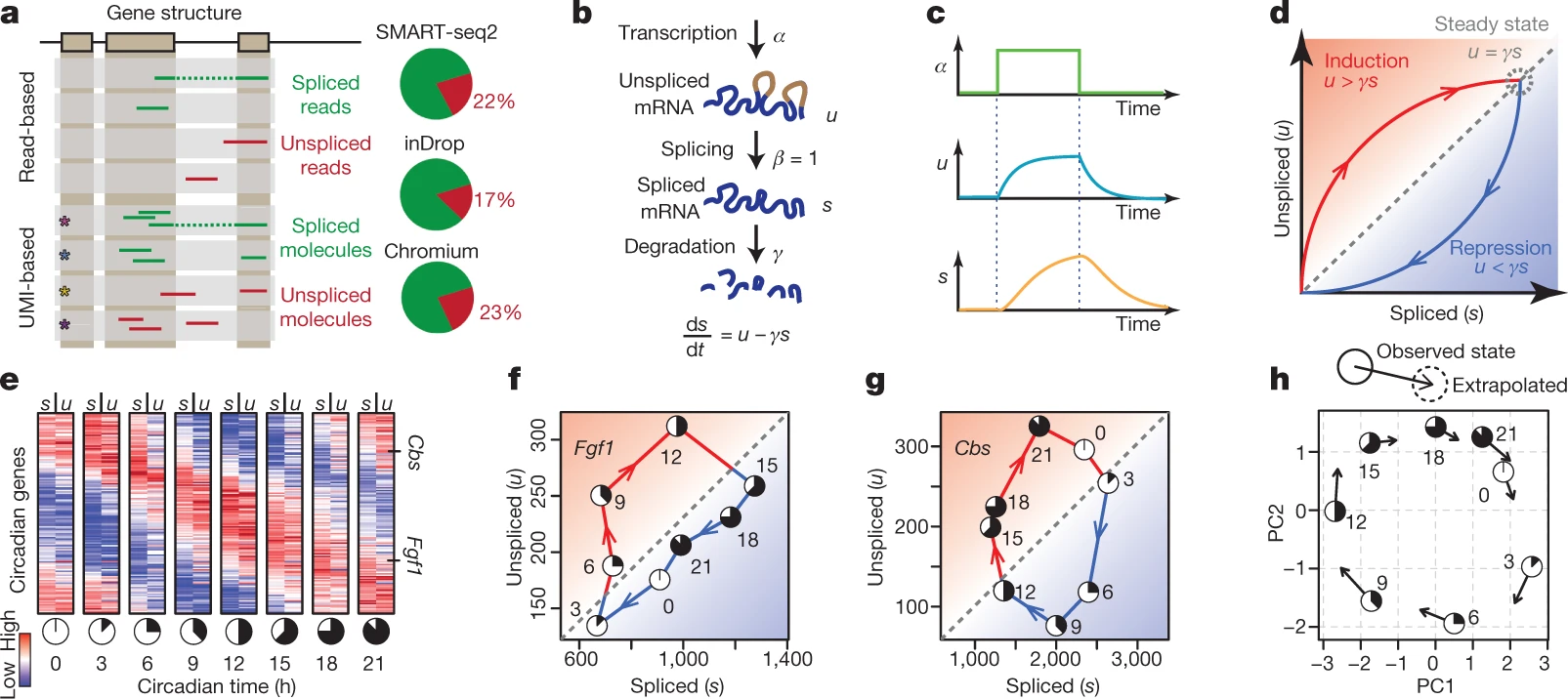
a, 通过分别计算包含内含子序列的读段来估计已剪接和未剪接的计数。多个与特定分子相关的读段被组合在一起（带星号的框）用于基于唯一分子标识符（UMI）的协议。饼图显示了未剪接分子的典型比例。 b, 转录动态模型，捕获了产生未剪接（u）和已剪接（s）mRNA 产物所涉及的转录（α）、剪接（β）和降解（γ）率。 c, 模型 b 的时间函数解，显示对 α 的阶跃变化响应的未剪接和已剪接 mRNA 动态。 d, 相位图显示了与 c 中显示的相同解（实线曲线）。不同转录率 α 的稳态在由斜率 γ（虚线）给出的对角线上。未剪接 mRNA 的水平高于或低于这个比例分别表示基因表达的增加（红色阴影）或减少（蓝色阴影）。 e, 在 24 小时时间进程中，小鼠肝脏中与昼夜节律相关的基因的已剪接（s）和未剪接（u）mRNA 的丰度。未剪接的 mRNA 可预测下一时间点的已剪接 mRNA。 f, g, 一对受昼夜节律驱动的基因 Fgf1（f）和 Cbs（g）的相位图。每个点的昼夜时间使用时钟符号显示（与 e 中的相对应）。虚线对角线显示了由 γ 拟合预测的稳态关系。 h, 模型预测的未来时间 t 的表达状态变化，在第一和第二主成分（PCs）的空间中显示，重现了沿昼夜周期的进展。每个圆显示观察到的表达状态，箭头指向从速度估计外推的未来状态位置。

为了量化前体 mRNA 和成熟 mRNA 丰度之间的时间依赖关系，我们假设了一个简单的转录动态模型 2，在该模型中，已剪接 mRNA 丰度的一阶时间导数（RNA 速度）由未剪接 mRNA 生成已剪接 mRNA 和 mRNA 降解之间的平衡决定（图 1b 及补充说明 1）。在这样的模型下，当转录率 α 恒定时，稳态是渐近接近的，已剪接（s）和未剪接（u）分子的稳态丰度由 α 决定，并受到固定斜率关系 u = γs 的约束（补充说明 2 第 1 节）。平衡斜率 γ 结合了降解和剪接率，捕获了基因特异性的调控属性，内含子和外显子长度的比例，以及内部引物位点的数量。使用最近发布的小鼠组织汇编 11，我们发现大多数基因在广泛的细胞类型中的稳态行为与单一固定斜率 γ 一致（扩展数据图 3a-c）。然而，11% 的基因在不同组织的子集中显示出不同的斜率（扩展数据图 3d, e），这表明组织特异性的选择性剪接（扩展数据图 3f）或降解率。

在动态过程中，转录率 α 的增加首先导致未剪接 mRNA 的快速增加，随后是已剪接 mRNA 的增加（图 1c 及补充说明 2 第 1 节），直至达到新的稳态。相反，转录率的降低首先导致未剪接 mRNA 的快速下降，然后是已剪接 mRNA 的减少。在基因表达的诱导过程中，未剪接 mRNA 的存在量超过基于平衡率 γ 的预期，而在抑制过程中则相反（图 1d）。因此，未剪接和已剪接 mRNA 的丰度平衡是成熟 mRNA 丰度未来状态的指示器，从而也是细胞未来状态的指示器。

为了展示如何使用这个简单模型来预测成熟 mRNA 丰度的未来变化，我们检查了小鼠肝脏中昼夜周期的批量 RNA-seq 测量的时间序列 12。每个时间点的未剪接 mRNA 水平与随后时间的已剪接 mRNA 更为相似（图 1e），许多与昼夜节律相关的基因在上调期间显示出预期的未剪接 mRNA 相对于斜率 γ 的过量，以及在下调期间的相应不足（图 1f, g）。解决所提出的每个基因的微分方程允许我们在整个昼夜周期中外推每次测量，准确捕获昼夜周期进展的预期方向（图 1h）。

接下来，为了展示预测单细胞测量中的转录动态的能力，我们分析了最近发布的小鼠嗜铬细胞 13 的单细胞 mRNA-seq 数据，使用 SMART-seq25（图 2）。在发育过程中，大量的嗜铬细胞（肾上腺髓质的神经内分泌细胞）起源于施万细胞前体，提供了一个方便的测试案例，其中分化的方向可以通过谱系追踪来验证。许多基因的相位图显示了与预测的稳态关系的预期偏差（图 2b, c）。个别细胞的 RNA 速度估计准确重现了这个数据集中的转录动态，包括不同分化细胞向嗜铬命运的一般移动（图 2d），以及向中间分化状态的移动和远离。速度还捕获了嗜铬细胞分化中涉及的细胞周期动态，无论是在主成分分析（PCA）投影中还是在聚焦分析细胞周期相关基因时（补充说明 2 第 5 节）。

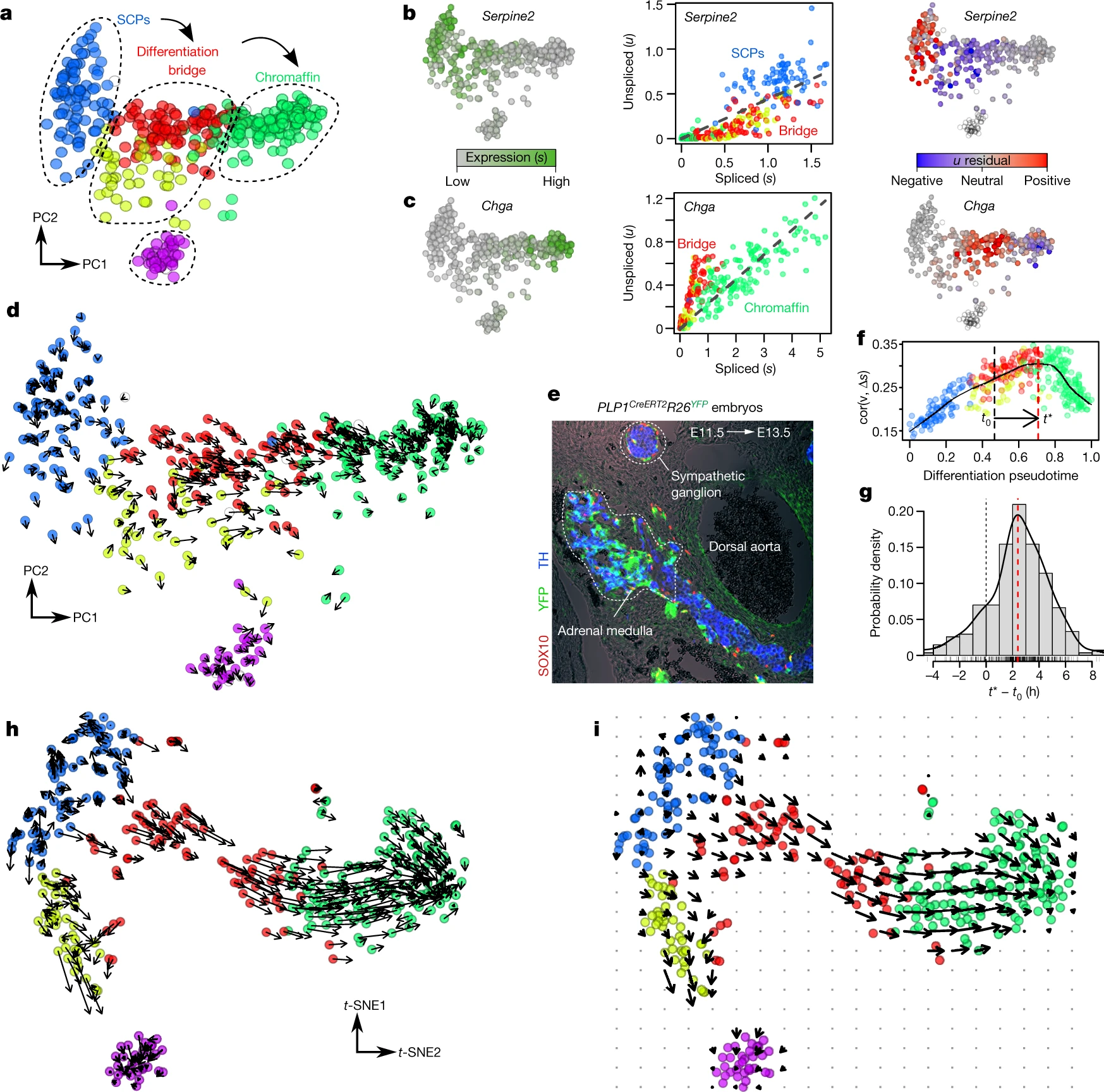
a, PCA 投影显示了在胚胎日（E）12.5 的小鼠中，施万细胞前体（SCPs）分化为嗜铬细胞的主要亚群（n = 385 个细胞）。 b, c, 为被抑制的 Serpine2（b）和被诱导的 Chga（c）基因显示表达模式（左侧）、未剪接 - 已剪接相位图（中心，细胞根据 a 着色）和 u 残差（右侧）。读取计数是在五个最近邻细胞间汇总的。 d, 显示在第一和第二主成分（PCs）上的观察状态和外推的未来状态（箭头）。RNA 速度估计没有进行细胞或基因汇总。 e, 通过使用特异于 SCP 的 PLP1-CreERT2 线的谱系追踪证实了 SCP 到嗜铬细胞的转变。显示了发育中的肾上腺髓质的横截面。注意发育中的髓质中 TH+YFP+ 细胞的高比例以及交感神经节中此类双阳性细胞的缺失（n = 3 个重复）。 YFP 标记 Htr3a+ 桥接细胞；TH 标记嗜铬细胞；TH+YFP+ 标记了从桥接群体新分化的嗜铬细胞。 f, 在假时间 t0 的基础上，根据速度 v 与细胞表达差异之间的相关性（y 轴），估计单个细胞沿嗜铬细胞分化轨迹的外推距离。红线显示最优外推时间（t）（见补充说明 2 第 6 节）。 g, 嗜铬细胞分化时间进程的最优外推时间（t - t0）的分布。红线标记分布模式（2.1 小时）。 h, 在原始出版物 13 中预定义的 t-SNE 图上可视化速度。基于最近邻细胞汇总（k = 5）的速度估计被使用。 i, 使用高斯平滑在规则网格上可视化与 h 相同的速度场。

我们的速度估计程序包含了几个特征，以适应剪接生物学的复杂性（补充说明 1）。基因特异性平衡系数 γ 的估计是通过对极端表达分位数进行回归分析来进行的，即使大多数观察到的细胞处于非稳态时，也能确保估计的稳健性（补充说明 2 第 2 节）。为了适应远离稳态观察到的基因，我们还开发了一种基于基因结构的替代拟合方法（扩展数据图 4）。可以使用多种技术在低维度中可视化速度估计。观察到的和外推的细胞状态可以共同嵌入到一个共同的低维空间中（例如，图 2d 中的 PCA）。或者，可以基于外推状态与局部邻域中其他细胞的相似性，将速度投影到现有的低维嵌入中，如 t 分布的随机邻域嵌入（t-SNE）（图 2h，见补充说明 1）。在大型数据集中，使用局部平均向量场更容易可视化细胞速度的普遍模式（图 2i）。由于细胞可以同时沿多个独立组分具有 RNA 速度，如分化、成熟和增殖，因此在解释低维表示时必须谨慎，因为在某个特定嵌入中看似无速度的细胞在某些未可视化的子空间中可能具有显著的速度。

细胞特异性的 RNA 速度估计为细胞命运的定量模型提供了自然基础。代谢标记显示，对于大多数基因，剪接/未剪接比例的变化可以在 10-100 分钟后被检测到（扩展数据图 2）。另一方面，外推的有效时间尺度取决于被分析的生物过程。基于对嗜铬祖细胞用 5- 乙炔基 -2′- 脱氧尿苷（EdU）进行脉冲标记（补充说明 2 第 6 节），我们估计我们能够将时间外推 2.5-3.8 小时（图 2f, g），这也与解析细胞周期事件的能力相符。然而，由于外推的线性特性，这种预测时间尺度将依赖于基因表达轨迹的形状（即表达流形的曲率）。通过在观察到的表达流形上追踪一系列小的外推步骤，可以预测更长时间尺度的细胞命运（补充说明 2 第 7 节）。

为了展示我们方法的普适性，我们分析了使用额外的单细胞 RNA 测序协议生成的数据。我们观察了使用 inDrop 协议测量的小鼠骨髓中的中性粒细胞成熟以及小鼠皮层中光诱导的神经元激活的转录动态（扩展数据图 5），以及使用 10x Genomics Chromium7 测量的肠上皮（扩展数据图 6）、少突胶质细胞分化（扩展数据图 7）和海马体发育（见下文）。RNA 速度的估计对模型参数的变化以及基因和细胞的抽样具有较强的鲁棒性，其中最敏感的参数是在预定义嵌入中可视化速度所用的邻域大小（补充说明 2 第 10, 11 节）。大多数基因显示速度估计与经验观察到的表达导数之间的正相关（扩展数据图 8），证实了速度向量的信息性。在特定情况下的失败有几个明显的原因，包括远离平衡观察到的基因、非编码转录本的不均匀贡献，以及导致测量群体中多个 γ 率的选择性剪接（补充说明 2 第 4 节）。

接下来，我们将 RNA 速度应用于发育中的小鼠海马体的分支谱系研究 14。在去除了血管和免疫细胞，以及 GABA 能（γ- 氨基丁酸释放）和 Cajal-Retzius 神经元（这些神经元起源于海马体以外）后，t-SNE 图展示了一个具有多个分支的复杂流形（图 3a）。我们使用已知标记来识别对应于星形胶质细胞、少突胶质细胞前体（OPCs）、齿状回颗粒神经元和海马体五个区域的锥体神经元的分支尖端：齿状回、CA1、CA2、CA3 和海马沟（扩展数据图 9）。个别基因的相位图显示了沿着流形特定的基因表达的诱导和抑制（图 3b 和扩展数据图 10）。例如，Pdgfra（OPCs 的标记）在前 OPCs 中被诱导并在 OPCs 中维持；它在前 OPC 状态中显示出相应的正速度，但在 OPCs 中则是中性的。同样，Igfbpl1 在神经母细胞中特异性表达，并且从径向胶质细胞到神经母细胞显示出正速度，但从神经母细胞到两个主要神经分支的速度是负的。

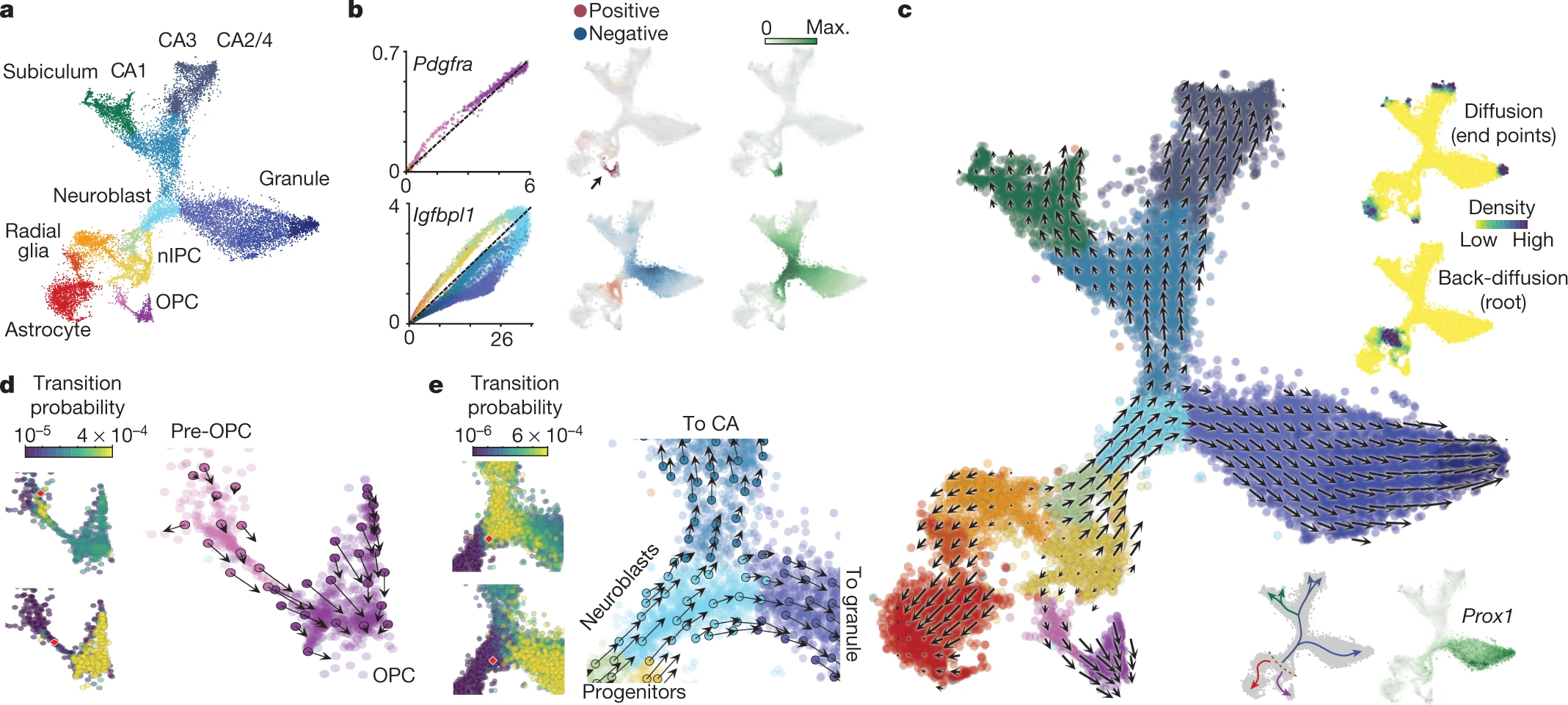
a, 发育中的小鼠海马体细胞的 t-SNE 图（n = 18,213 个细胞），显示出主要的暂态和成熟亚群。b, 两个受调控基因的相位图（左侧，颜色如 a 所示）、未剪接残差（中间）和已剪接表达（右侧）展示出来。使用了 k 最近邻（kNN）细胞池化。c, 速度场投影到 t-SNE 图上。箭头显示在规则网格上计算的局部平均速度。右上角插图，通过基于速度的转换概率的前向马尔可夫过程，流形上的高密度区域为分化终点；通过反向模拟过程识别分支树的根。右下角插图，RNA 速度场的概要示意图，以及转录因子 Prox1 的表达。d, 承诺到少突胶质细胞命运。左侧，从两个起始细胞（红色）到邻近细胞的单步转换概率的可视化。右侧，在 c 中的 t-SNE 图上显示的一部分细胞的速度。e, 神经母细胞的命运决定。左侧，从两个起始细胞（红色）到邻近细胞的单步转换概率的可视化。右侧，在 c 中的 t-SNE 图上显示的一部分细胞的速度。

RNA 速度显示了海马体中向量场的每一个主要分支（图 3c 和扩展数据图 10），起源于一小群排列成带状的细胞（图 3c，插图，虚线）。我们根据标记的表达，包括 Notch 靶基因 Hes1 和同源盒转录因子 Hopx（扩展数据图 9）的表达，将这些细胞识别为径向胶质细胞。实际上，命运绘图已经表明径向胶质细胞是海马体谱系树的真正起源 15。使用基于速度场的马尔可夫随机漫步模型，可以自动识别终端和根状态（图 3c），展示了 RNA 速度在没有先验发育过程知识的情况下定向谱系树的能力。在一侧，速度指向星形胶质细胞（表达 Aqp4），中间没有细胞分裂，或者交替指向前 OPC 状态，通过一条狭窄通道通向增殖的 OPCs。我们推测这条狭窄通道代表了对少突胶质细胞谱系的承诺的时刻。在这个微观状态级别上，命运选择很可能是一个非确定性过程，涉及倾斜基因表达以支持一个或另一个命运，一旦建立了转录因子反馈回路，最终命运就会被锁定 16。比较从前 OPCs 中开始的细胞与从通往 OPCs 的狭窄通道开始的细胞的未来状态概率分布，发现了明显的差异——后者细胞极有可能成为完全形成的 OPC，而前者则有可能保持在前 OPC 状态（图 3d）。

一些周期性的祖细胞（扩展数据图 9b）表达了神经发生转录因子（例如，Neurod2, Neurod4, Eomes），这些细胞的速度指向未成熟的神经母细胞状态，指向流形上部的三个主要神经分支。齿状回颗粒神经元首先从海马体本体分离出来，第二次分裂将海马细胞分成齿状回/CA1 和 CA2–4（扩展数据图 9, 10），符合海马体的主要功能和解剖学分区。详细的单细胞视角的分支谱系让我们能够审查命运选择。检查在 CA 和颗粒命运分支点入口处的两个相邻神经母细胞（图 3e），我们发现尽管它们当前状态在基因表达空间是邻居，它们的未来已经倾向于不同的命运，通过激活 Prox1 区分开来（图 3c，插图）。与这些发现一致的是，已经表明 Prox1 对形成颗粒神经元是必需的，当 Prox1 被删除时，神经母细胞会选择锥体神经元的命运 17。

为了证明 RNA 速度在人类胚胎中是可检测的，我们对怀孕十周的发育中的人类前脑进行了基于滴液的单细胞 mRNA 测序，重点关注谷氨酸能神经元谱系（图 4a）。我们发现一个强烈的速度模式，起始于增殖的祖细胞状态（径向胶质细胞），并通过一系列中间神经母细胞阶段，进展到表达 SLC17A7（前脑兴奋性神经元中使用的囊泡谷氨酸转运体，也称为 VGLUT1）的更成熟的分化谷氨酸能神经元。我们通过多重原位杂交验证了已知和新发现的皮层神经元发育标记的表达（图 4b, c），确认了在脑室区（径向胶质细胞；标记为 SOX2）的 CLU 和 FBXO32，在中间区（神经母细胞；标记为 EOMES）的 UNC5D 以及在皮质板（神经元；标记为 SLC17A7）的 SEZ6 和 RBFOX1 的预测表达。这些基因在组织中的层状表达（图 4c）与单细胞 RNA 测序数据中它们表达的伪时间分布紧密对应（图 4b）。

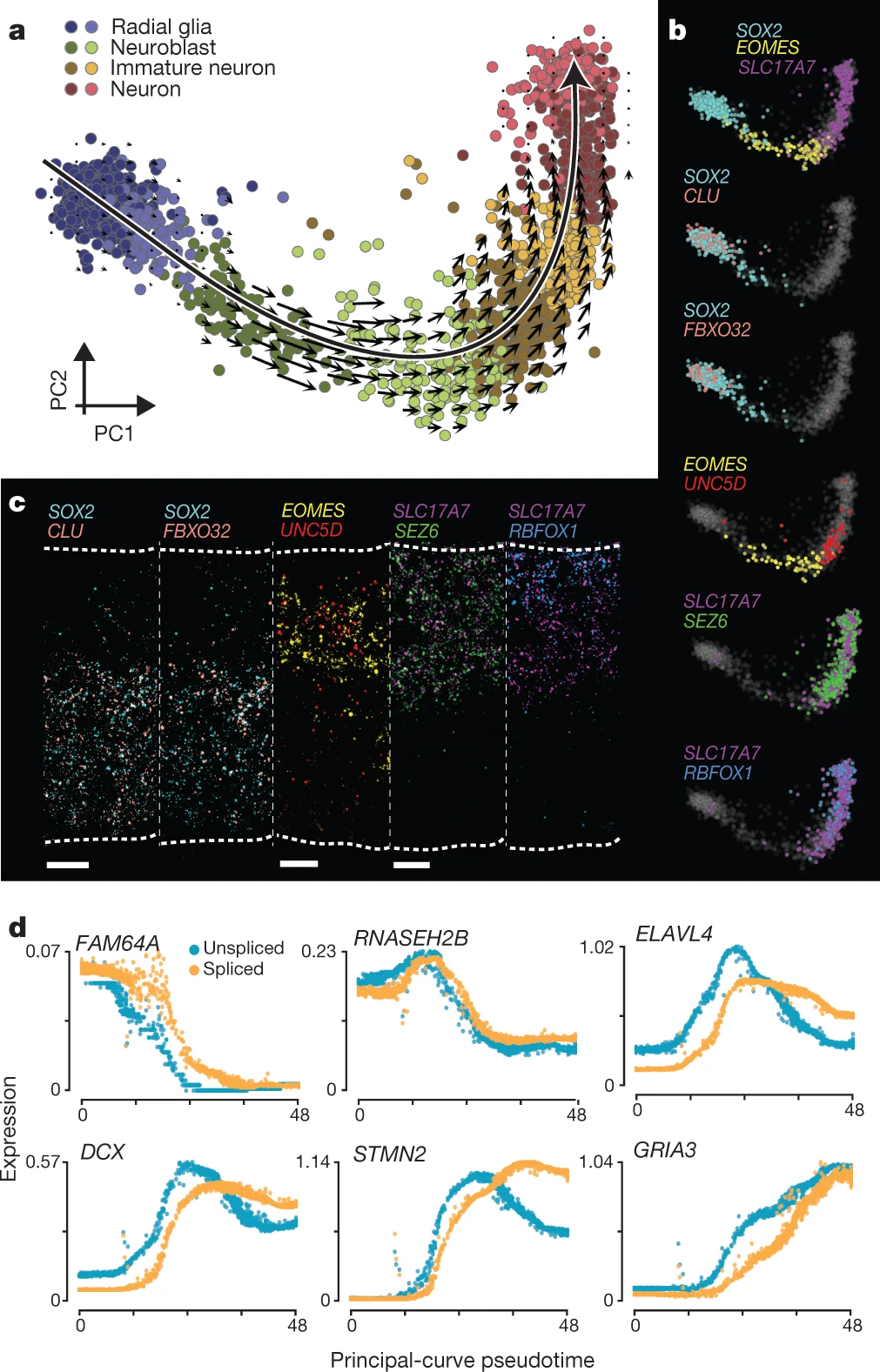
a, 人类谷氨酸能神经元分化的 PCA 投影（n = 1,720 个细胞），显示了在受孕后 10 周时的速度场。颜色表示细胞类型和中间状态。相应的主曲线以粗线显示。 b, 在 PCA 投影上，用伪色显示了已知的径向胶质细胞（SOX2）、神经母细胞（EOMES）和神经元（SLC17A7）标记的基因表达，以及新发现的标记基因的表达。 c, 在人类发育中的皮层横切面上，使用荧光原位杂交（RNAscope）对与 b 中相同的基因进行了检测，取向以脑室区朝下，皮质表面朝上（n = 1）。比例尺，25 微米。 d, 在谷氨酸能神经元成熟过程中的伪时间表达剖面，展示了六个示例基因。剪接丰度乘以 γ 以匹配未剪接丰度的比例。

我们使用主曲线分析对细胞进行排序，根据分化的伪时间来排列，并检查了人类原代细胞中转录的时间进程。我们确认，在上调和下调过程中，未剪接的 mRNA 始终先于剪接的 mRNA（图 4d）。我们观察到快速和慢速的动力学。例如，RNASEH2B 表现出快速动力学，未剪接和剪接 RNA 之间的差异很小。相比之下，如 DCX、ELAVL4 和 STMN2 等基因显示了最初的快速转录爆发，随后是在较低水平上的持续转录（由未剪接 RNA 曲线的形状证明，图 4d），剪接转录本的轨迹明显延迟。这种动态诱导超调被提出有助于快速诱导降解动力学慢的基因 2，但这在人类胚胎中尚未能够研究。

由于 RNA 速度基于实际的转录动力学，这种方法有望为我们理解分化过程中细胞在基因表达空间中的动态带来更坚实的定量基础。我们设想未来的流形学习算法将同时拟合流形及其上的动力学，基于 RNA 速度。RNA 速度已经使得在整个生物体中研究动态过程成为可能 18，并将极大地促进特别是在人类胚胎中的谱系分析。

方法¶

样本量的确定¶

没有使用统计方法预先确定样本量。实验没有随机化。在实验和结果评估期间，研究人员并未对分配情况进行盲目处理。

RNA 速度的理论描述¶

基于图 1 所示的转录模型，我们开发了一个用于稳健推断 RNA 速度的计算框架。理论和计算方法的详细描述可在补充说明 1 中找到。

分析流程、参数和实现¶

我们将上述程序实现为两个完整的流水线，一个用 R 语言（velocyto.R），一个用 Python（velocyto.py）。这些被用来生成本文中的所有分析，详细设置如下各节所述。

剪接和未剪接读段的注释¶

使用 velocyto.py 命令行工具对所有协议的读段进行注释。velocyto.py 的注释从 BAM 文件开始。对于 10x 基因组平台的数据集，使用 Cellranger 软件（10x Genomics）的默认参数处理 BAM 文件。对于 inDrop 数据集，使用 dropEst 管道进行读段的解复用，使用‘-F -L eiEIBA’选项生成类似于 Cellranger 输出的注释 BAM 文件。对于 SMART-seq2 数据，解复用的特定于细胞的 BAM 文件直接输入到 velocyto.py 中。使用 Cellranger 预构建包中的基因组注释 GRCm38.84 和 GRCh37.82 来计数分子，同时将其分为三类：‘剪接’、‘未剪接’或‘模糊’。

注释过程仅考虑了能够唯一映射的读段。具有多重映射的读段和映射到基于 UCSC 基因组浏览器重复掩蔽器输出的重复掩蔽区域内的读段被丢弃。对于基于 UMI 的协议，计数在分子水平进行，同时考虑与该分子相关的所有读段（支持读取集）的注释（如剪接、未剪接等）。每个分子的支持读取集是通过细胞条形码和 UMI 序列的组合确定的。对于 inDrops 数据集，由于 UMI 条形码的复杂性不足以在数据集中唯一标识一个分子，读段根据细胞条形码、UMI 以及其映射的基因组区域（以 10 兆碱基对为单位划分的染色体区域）进行分组。对于每个分子，考虑了所有与给定读段映射集兼容的已注释转录本，并且丢弃了与给定分子相关的读段集不兼容任何已注释转录本模型的情况。同样，如果一组支持读段映射与两个或多个不同基因的转录本模型兼容的情况也被丢弃。

应用以下规则集来注释支持给定分子的读段集为剪接、未剪接或模糊：

如果支持给定分子的所有读段集仅映射到兼容转录本的外显子区域，则将该分子注释为剪接。
如果所有兼容的转录本模型中至少有一个读段在支持该分子的读段集中跨越外显子 - 内含子边界，或映射到该转录本的内含子，则将该分子注释为未剪接。
如果一些兼容的转录本模型仅有外显子映射，而其他包含内含子映射，则将该分子注释为模糊，不用于下游分析。

在注释和计数 SMART-seq2 数据集的读段时应用了类似的逻辑，不过有以下显著差异：（1）由于读段缺乏 UMIs，每个读段被视为一个独立的分子；（2）由于协议不区分链，因此在注释每个读段时考虑了双链上的转录本注释。

嗜铬细胞数据集处理¶

图 2 的数据分析。胚胎日（E）12.5 和 E13.5 的小鼠嗜铬细胞数据集采用 velocyto.R 管道进行处理。根据一系列过滤标准计算 γ 系数和速度估计：γ ≥ 0.1；s（剪接）和 u（未剪接）之间的 Spearman 秩相关系数 ≥ 1；至少一个细胞亚群（簇）的基因 s 计数平均值 ≥ 5；至少一个细胞亚群的基因 u 计数平均值 ≥ 1；对于标注了跨越读段的数据集（E12.5，E13.5），要求至少一个亚群的平均跨越读段计数 ≥ 5。对于 SMART-seq2 数据集，由于跨越内含子和外显子边界的读段丰度足够高，可以估计未剪接偏移 o。偏移量是通过线性回归估计的。

小鼠海马数据集分析¶

图 3 的数据分析。共分析了 18,213 个细胞（出生后第 0 天（P）：8,113 个细胞；出生后第 5 天（P）：10,100 个细胞）。使用 pagoda2（https://github.com/hms-dbmi/pagoda2）计算相关性相似性矩阵上的嵌入。简要地，通过在表达量上拟合广义加性模型来进行基因方差标准化，并通过匹配 F 分布的对数残差的尾部概率与自由度对应于细胞总数的 χ^2 分布来重新缩放基因方差。细胞距离确定为 1 - rij，其中 rij 是细胞 i 和 j 在数据集前 3000 个变异基因的前 100 个主成分上的 Pearson 线性相关。使用 Louvain 社区检测算法在最近邻细胞图上进行聚类（k = 30，pagoda2 实现）。对于速度分析，排除了表达低的（剪接的）基因（要求最小表达计数 40 并在 30 个以上细胞中检测到），并根据非参数拟合的变异系数（CV）选择了前 3000 个高变异基因，使用平均值作为预测器（使用支持向量回归）。只有 1,706 个基因的未剪接分子计数超过检测阈值（最小表达计数 25 并在 20 个以上细胞中检测到），才保留用于分析。为了校正细胞大小，将计数除以每个细胞中的分子总数，并乘以所有细胞中的分子平均数。剪接和未剪接计数分别进行归一化。为了降低维度，进行 PCA 并保留基于解释方差比例配置文件的前 19 个变异组分。在这个降维的 PCA 空间中使用欧几里得距离构建 kNN 图（k = 500），使用一个贪心平衡 kNN 算法，限制每个节点最多有 4k 的传入边。使用该图进行 kNN 池化。基于模型 I 假设进行速度基的外推。

人类谷氨酸能神经发生分析¶

图 4 的数据分析。通过在前四个主成分空间内拟合主曲线进行伪时间分析（使用 R 包 princurve）。将细胞位置投影到曲线上，投影间的弧长用作伪时间坐标。使用速度场确定伪时间的方向。在同一子空间中的最近邻图上使用 Louvain 社区检测算法确定簇。对于速度分析，排除了表达低的（剪接的）基因（要求最小表达计数 30 并在 20 个以上细胞中检测到）。根据非参数拟合的 CV 与平均值（使用支持向量回归）选择前 2000 个最变异的基因。总共保留了 987 个基因，其未剪接分子在检测阈值以上（要求最小表达计数 25 并在 20 个以上细胞中检测到；一个亚群中基因的平均剪接计数为 0.06，未剪接计数为 0.007）。为了校正细胞大小，将计数除以每个细胞中的分子总数并乘以所有细胞中的分子中位数。对于细胞 kNN 池化，基于前六个主成分空间的欧几里得距离构建 k 最近邻图（k = 550），如上所述。使用极端分位数拟合法和对角分位数拟合 γ 系数，如上所述。

分析不同细胞类型中的 γ 系数：Tabula Muris 数据集¶

数据分析扩展图 3¶

分析了仅包含通过 10x Genomics Chromium 协议生成的样本的 Tabula Muris 数据集。使用 velocyto.py 处理 BAM 文件和作者提供的有效条形码列表。所有实验数据被合并为单一数据集。计算不同已注释细胞类型的剪接和未剪接原始分子计数的平均值，并计算了 Pearson 相关系数。为减少细胞覆盖率变异带来的偏差，我们从分析中移除了细胞数量少于 120 的簇以及细胞数超过 3000 的几个异常簇。也排除了红细胞，因为它们缺乏核。为避免在只有一两种细胞类型表达某基因的琐碎情况中膨胀我们的相关性，我们应用了以下过滤器：仅当基因的表达水平满足所有以下条件时才考虑：（1）至少有 5 种细胞类型的平均剪接分子数至少为 0.04；（2）至少有 4 种细胞类型的平均未剪接分子数至少为 0.02；（3）表达最高的细胞类型平均至少有 0.15 的剪接分子；（4）至少有 2 种其他细胞类型的表达水平至少为最高表达细胞类型的 15%。此外，为避免由零值膨胀相关性估计，每个基因的相关性仅考虑表达该基因的细胞类型，最低表达水平为剪接 10^-5 和未剪接 5×10^-6。扩展数据图 3 中提供的 γ 估计值是通过不带截距的 RANSAC 回归斜率获得的。使用由期望最大化拟合的混合广义线性回归模型估计了双 γ 值，如 R 包 flexmix 中实现的那样。通过比较双 γ 模型与单 γ 广义线性模型的拟合，估计了有两个或更多 γ 值比单一 γ 值更好解释的基因比例。具体地，使用了对数似然比测试，差异自由度等于细胞类型数 +1。应用了 Bonferroni 校正，P < 0.05 的基因被报告为由两个 γ 更好地解释。

肠上皮细胞分析¶

扩展数据图 6 的数据分析。使用 velocyto.py 运行 BAM 文件和作者提供的有效条形码列表。过滤掉剪接分子数<2000 和未剪接分子数<300 的细胞。根据基因本体注释（使用 Goatools）从分析中移除了细胞周期基因。在数据集中至少有 30 个剪接分子和 20 个未剪接分子的基因被用于下游分析。没有进行聚类，而是使用原始出版物中的细胞类型注释。使用这些簇进行特征选择。具体地，每个簇中上调表达最多的 110 个基因被选中。删除了在表达最高的簇中平均表达量低的基因（未剪接<0.008，剪接<0.08）。对细胞大小归一化的数据进行 PCA，保留了前九个主成分，并用于计算 t-SNE 图（cytograph 实现，欧几里得距离）。我们使用前九个主成分空间中的 70 个最近邻计算了细胞 kNN 池化。使用默认参数拟合 γ 值，计算速度，并使用模型 II 进行外推，其中 t 设置为 4。使用 n_sight 为 30 的平方根方差稳定变换计算转换概率。

人类组织和单细胞 RNA 测序¶

图 4 的数据分析。人类第一学期前脑组织来自选定的常规堕胎（受孕后 10 周），已取得孕妇书面知情同意，并符合由区域伦理审查委员会（瑞典斯德哥尔摩，参考编号 2007/1477-31/3；用于 scRNA-seq）以及英国剑桥 Addenbrooke’s Hospital 的东英格兰 - 剑桥中央国家研究伦理服务委员会（当地研究伦理委员会，参考编号 96/085；用于原位杂交）的伦理许可。收集的人类胎儿前脑组织在 Hibernate-A（Thermo-Fisher）冷藏培养基中存储，并添加了 GlutaMAX 和 B-27 补充剂，按照制造商的说明（过夜，4°C）。然后将组织切成大约 1-2 毫米长的小立方块。使用 Miltenyi 的神经组织解离试剂盒（P）按照制造商的说明解离组织。简要地，将组织准备在含有 0.067 mM β- 巯基乙醇的试剂盒缓冲液中。添加酶混合物 1 和 2 后，使用逐渐变小的火磨的巴斯德吸管机械解离组织，分别上下吸 20 次，15 次和 10 次。最后，收集的细胞存放在含有 1% BSA 的 PBS 中并立即准备进行单细胞文库制备。使用 10x Genomics Chromium V2 套件进行单细胞 RNA 测序，按照制造商的协议操作，并在 Illumina Hiseq 2500 上进行测序。

动物实验的伦理合规性¶

所有实验程序遵循瑞典动物保护立法的指南和建议，并由当地实验动物伦理委员会批准（N68/14，Stockholms Norra Djurförsöksetiska nämnd，瑞典）。

报告摘要¶

有关实验设计的更多信息，请参阅与本文相关的《自然研究报告摘要》。

代码可用性¶

本文描述的软件以一个名为 Velocyto 的管道形式提供，可在 http://velocyto.org 获取。这包括完整的 R 和 Python 分析库以及 R 和 Python 笔记本。

补充说明 1：理论与计算方法¶

RNA 速率的理论描述¶

基于图 1 所示的转录模型，我们可以为单个基因列出速率方程，这些方程描述了未剪接 mRNA 分子 $u$ 和剪接分子 $s$ 随时间的预期数量变化：

\[ \begin{aligned} & \frac{d u}{d t}=\alpha(t)-\beta(t) u(t) \\ & \frac{d s}{d t}=\beta(t) u(t)-\gamma(t) s(t) \end{aligned} \]

第一个方程表示未剪接 mRNA 相对于时间的变化速率等于已转录的 mRNA 分子减去剪接速度

第二个方程则表示已经剪接好的 mRNA 相对于时间的变化速率是剪接速率减去降解速率

其中，$\alpha(t)$ 是时间依赖的转录速率，$\beta(t)$ 是剪接速率，$\gamma(t)$ 是降解速率。在假设速率常数（时间独立）$\alpha(t)=\alpha, \gamma(t)=\gamma$，并将 $\beta(t)=1$ （即以剪接速率的单位测量所有速率）的条件下，速率方程简化为：

即以剪接速率作为单位元

\[ \begin{aligned} & \frac{d u}{d t}=\alpha-u(t) \\ & \frac{d s}{d t}=u(t)-\gamma s(t) \end{aligned} \]

速率方程的完整解如下：

\[ u(t)=\alpha\left(1-e^{-t}\right)+u_0 e^{-t} \]

\[ s(t)=\frac{e^{-t(1+\gamma)}\left[e^{t(1+\gamma)} \alpha(\gamma-1)+e^{t \gamma}\left(u_0-\alpha\right) \gamma+e^t\left(\alpha-\gamma\left(s_0+u_0+s_0 \gamma\right)\right)\right]}{\gamma(\gamma-1)} \]

初始条件为 $u(0)=u_0$ 和 $s(0)=s_0$。在上述假设下，该解决方案可用于将 mRNA 丰度 $s$ 外推到未来时间点 $t_1$，通过输入细胞的当前状态 $u_0$ 和 $s_0$，然后计算 $s\left(t_1\right)$。

上述方程适用于单个基因。对于所有基因，相同的方程在相同假设下成立，但具有基因特异性的速率常数。请注意，对所有基因设置 $\beta(t)=1$ 意味着我们假设一个共同的、恒定的剪接速率。这种简化假设减少了需要估计的参数数量，使得从单细胞 RNA 测序数据估计速率成为可能。然而，对基因特异性剪接速率的额外实验数据将允许放宽这一假设并提高外推精度。

请注意，上述方程是速率方程，是确定性的且连续值的。速率方程给出了观察到的 mRNA 分子数量的期望值随时间的演化，而不是每个时间点的确切观察数量。例如，如果速率方程给出 $s(20)=14.3$，则 14.3 是时间 $t=20$ 时剪接 mRNA 分子的期望数量（在统计意义上）。

主方程：在化学反应系统中，主方程提供了所有反应物种的计数的完整概率分布，作为时间的函数，通常表示为 $\Psi$。在任何给定的时间点，$\Psi(x, y, t)$ 为分子 $u(t)=x$ 和 $s(t)=y$ 的每种可能配置分配一个概率，其中 $\sum_x \sum_y \Psi(x, y, t)=1$。我们注意到，我们的模型是一个只包含单分子反应的开放系统，对于这种系统，主方程有一个精确的解析解。非正式地，如果系统以泊松分布的变量开始，它们将保持泊松分布。如果它从任何其他状态开始，那么它将迅速收敛到泊松分布。此外，泊松分布的变量的速率常数等于上述速率方程的解。因此，我们模型的主方程是泊松分布的乘积：

\[ \Psi(x, y, t) \sim \mathcal{P}(x, y ; u, s) \]

其中 $u$ 和 $s$ 是速率方程的解（在时间 $t$），$\mathcal{P}$ 表示双变量乘积泊松分布，其概率密度函数为

\[ f(x, y ; u, s)=\frac{e^u u^x}{x !} \frac{e^s s^y}{y !} \]

估算与外推。归一化降解率 $\gamma$ 在不同基因之间会有所不同，需要以基因特异性方式进行估算。在稳态种群中，其中 $d s / d t=0$，我们可以将未剪接和剪接 mRNA 分子的比例确定为给定基因的 $\gamma$（同样设置 $\beta=1$）：

\[ \begin{aligned} & \gamma=\frac{u}{s} \\ & \alpha=u \end{aligned} \]

对于已知为末端分化的种群中表达的基因，稳态假设可能是现实的。然而，对于在发育过程中暂时表达的基因，或者在未取样到末端种群的情况下，稳态假设将失败。后续章节将详细说明如何在不假设稳态的情况下估算 $\gamma$。

更棘手的是，我们不知道 $\alpha$ 的值，也不容易估算。这阻止了我们将 $s(t)$ 外推到未来。因此，我们不是假设 $\alpha$ 是常数，而是使用以下两种替代假设之一来估算 $s(t)$：

模型 I. 恒定速率假设：

我们假设为了 $s(t)$ 的外推，剪接分子变化的速率保持不变。即，我们假设 $d s / d t=v$ 是恒定的，这样剪接 mRNA 分子当前的增加或减少速率会持续到未来。在此假设下，外推是简单的，因为

\[ s(t)=s_0+v t \]

换句话说，外推相当于取当前的 mRNA 分子数量并加上当前变化速率与外推时间步长的乘积。只要时间步长较短，这种假设在实践中效果很好。对于更长时间的外推，如果 $v<0$（即在基因下调的情况下），$s(t)$ 可能变成负值。这需要在零值处剪切。

模型 II. 未剪接分子恒定假设：

另一种方法是假设未剪接分子的数量保持恒定，即 $u(t)=u_0$，来外推 $s(t)$。这将问题简化为一个单一的速率方程：

\[ \frac{d s}{d t}=u_0-\gamma s(t) \]

然后解变为

\[ s(t)=s_0 e^{-\gamma t}+\frac{u_0}{\gamma}\left(1-e^{-\gamma t}\right) \]

实践中，我们发现在短时间外推尺度上，这两种方法得到了非常相似的结果。我们将在下文指出何时使用模型 I 或模型 II。

假设基因独立，细胞的整体 RNA 速度是由各个基因速度组成的多维向量。

估算框架¶

在本节中，我们将描述用于估算 RNA 速度及相关数据分析的分析框架。这种分析逻辑分别在 $\mathrm{R}$ 和 Python 环境中由 velocyto 实现，具体为 $\mathrm{R}$ 包和 velocyto.py 包。每个包实施的参数、阈值和其他相关信息将在下一节详细描述，并且在 http://velocyto.org 上的配套笔记本中提供了重现我们分析的代码。

速度估算程序纳入了多个特性以适应剪接生物学的复杂性。对剪接和未剪接计数的独立标准化允许控制细胞间剪接率的全基因组变化。我们的模型纳入了基因特异性偏移量以考虑可能源自其他转录本或对齐错误的背景信号。还可以使用几种进一步的调整来增强 RNA 速度估算，减少单细胞测量噪声和基因特异性异常的影响。通过跨最相似的 $k$ 个细胞汇集转录本计数可以提高 RNA 速度估算的稳健性（见下文的“细胞最近邻（kNN）汇集”部分）。类似地，可以基于假设这些基因也受到相同上调/下调动态影响的前提，跨相关性良好的基因进行计数汇集（见下文的“基因 kNN 汇集”部分，补充说明 2 图 8d）。

通过回归极端表达分位数来进行基因特异性平衡系数 $\gamma$ 的估算，这是计算速度的关键步骤（见下一节）。此程序即使在大部分（有时是全部）观测细胞处于非稳态的情况下也能确保估算的稳健性（补充说明 2 第 2 节）。然而，此默认拟合程序可能会系统性地低估那些远离其稳态观测到的基因的速度，例如在观测到的分化过程的最末端上调的嗜铬细胞成熟基因，或者在初始的施万细胞前体阶段已经被积极下调的神经嵴基因。为了解决这一限制，我们开发了一种基于结构的替代拟合方法，以预测基于基因的结构参数（如表达的外显子数量、内源引物位点或内含子长度）的剪接和未剪接 RNA 之间的稳态关系（扩展数据图 4）。所得的速度估算纠正了嗜铬分化轨迹极端的低估。

RNA 速度的估算：

对于每个基因，归一化的降解率 $\gamma$ 是通过最小二乘法拟合以下线性模型确定的：$u \sim \gamma * s$，其中 $u$ 和 $s$ 分别是观察到的给定基因在各个细胞中的大小归一化的未剪接和剪接丰度。请注意，为了控制剪接效率和未剪接分子检测的全局变异，剪接和未剪接计数分别进行归一化。具体来说，在给定的细胞中 $u=U / N_u, s=S / N_s$，其中 $U$ 和 $S$ 分别是未剪接和剪接计数的数量，$N_u$ 和 $N_s$ 分别是在给定细胞中观察到的未剪接和剪接分子的总数。可选择性地包括一个偏移量，以解释可能由未注释转录本驱动的基线内含子计数。

注意，以这种方式拟合 $\gamma$ 只在细胞处于稳态时（且远离零点时）是正确的。然而，通过使用强健的分位数拟合（即仅包括接近原点和相位肖像图右上角的细胞），我们发现 $\gamma$ 即使在大多数（甚至所有）细胞都处于非稳态的情况下也能得到相当好的近似（见补充说明 2 第 2 节）。

在模型 I 下，假设给定细胞中给定基因的速度分量 $\mathrm{v}$ 是恒定的，并估计为 $v=u-\gamma s-o$，其中 $o$ 是可选的偏移参数，用于考虑外来转录本的贡献。然后，确定给定细胞中给定基因的外推计数为 $s_t=\max \left(0, s_0+v t\right)$。其中 $t$ 是选择的外推时间步长，以确保每个细胞的总 RNA 计数没有显著变化。

在模型 II 下，假设 $\mathrm{u}$ 为常数，给定细胞中给定基因的剪接 mRNA 的位移 $\Delta s$ 估计为 $\Delta s(t)=\left(\frac{\hat{u}}{\gamma}-s\right)\left(1-e^{-\gamma t}\right)$，其中 $\hat{u}$ 是经偏移调整的未剪接计数，计算为 $\hat{u}=\max (0, u-o)$，并使用默认的外推时间 $t=1$。然后确定给定细胞中给定基因的外推计数为 $S_t=\max \left(0, S+\Delta s(t) N_s\right)$，其中 $S$ 是给定细胞中基因的未归一化剪接计数。然后计算归一化的外推计数为 $s_t=S_t / \widehat{N}$，其中 $\widehat{N}$ 是外推的细胞总大小 $\widehat{N}=N_s+S_t-S$。

由于不均一的损失导致的误差：

剪接和未剪接 mRNA 分子的计数在样本准备过程中受到基因特异性损失的影响。只要这些损失是相等的，观察到的计数 $\mathrm{U}$ 和 $\mathrm{S}$ 将仅是真实计数 $\widehat{U}$ 和 $\hat{S}$ 的线性缩放：

\[ \begin{aligned} & U=k \hat{U} \\ & S=k \hat{S} \end{aligned} \]

在缩放单位中，上述所有假设仍然成立。如果损失是以率 $k$ 均匀随机发生的，且 $\hat{U}$ 和 $\hat{S}$ 的分布是泊松分布的，那么 $U$ 和 $\mathrm{S}$ 也将保持泊松分布（如果它们是负二项分布也是如此，因为后者可以视为具有伽马分布率的泊松分布）。因此，$\mathrm{U}$ 和 $\mathrm{S}$ 的期望值及其分布将在新单位中得以保持。然而，相对方差会增加，因为观察到的分子较少。

然而，如果未剪接分子 $\mathrm{U}$ 的基因特异性损失与 $\mathrm{S}$ 不同，比如相差一个因子 $f$，那么我们对 $\frac{d s}{d t}$ 的估计将偏差一个因子 $f$。这可以如下理解。首先，在稳态下，我们将估计 $\gamma=\widehat{U} / \hat{S}$，实际上我们将估计 $f \gamma=f \widehat{U} / \hat{S}$。其次，在非稳态下，我们对速度的估计将是：

\[ f \widehat{U}(t)-f \gamma \hat{S}(t)=f(\widehat{U}(t)-\gamma \hat{S}(t))=f \frac{d \hat{S}}{d t} \]

非正式地说，这个因子的效果是为每个基因创建一个不同的时间尺度，加剧了假设恒定剪接率 $\beta$（上文提到）的效果。

细胞最近邻（kNN）汇集。为了改善 $\gamma$ 的估计，我们在局部邻域内汇集了计数数据。具体来说，我们用原始细胞及其 $k$ 个最近邻居的计数之和替代了 $S, U$ 的计数。$k$ 的选取适应了数据集的稀疏性和大小。速度的估算使用汇集的计数数据进行。外推状态使用初始（非汇集）计数值计算。在所有基因的对数尺度上使用皮尔逊线性相关距离找到 SMART-seq2 数据集中 $k$ 个最近的细胞，而在较大的 10x Chromium 和 inDrop 数据集中使用 PCA 空间的欧几里得距离。

细胞速度的可视化：

细胞的外推状态对应于与原始细胞测量相同空间的向量，可以直接使用如 PCA 等线性降维方法进行可视化。对于基于 PCA 的可视化（图 1h、图 2d），主成分是基于观察到的表达空间确定的。然后使用相同的特征向量的投影来定位速度箭头的尖端。

对于非线性、非参数嵌入，如 t-SNE（例如图 2h），将新数据点投影到嵌入中是具有挑战性的。因此，我们开发了一种方法，将速度箭头放置在表达差异与估计的速度向量最佳相关的方向上，并控制细胞密度分布。方向如下估计。我们通过在速度向量与细胞状态差异向量之间的皮尔逊相关系数上应用指数核，计算了过渡概率矩阵 $\boldsymbol{P}$：

\[ \boldsymbol{P}_{i j}=\exp \left(\frac{\operatorname{corr}\left(\boldsymbol{r}_{i j}, \boldsymbol{d}_i\right)}{\sigma}\right) \]

其中 $r_{i j}$ 是经方差稳定（逐元素）转换 $\varrho$ 变换后，细胞 $i$ 和 $j$ 的表达向量 $s_i$ 和 $s_j$ 之间的差向量，而 $\boldsymbol{d}_{\boldsymbol{i}}$ 是细胞 $i$ 的 $\varrho$ 变换后的速度外推向量：

\[ r_{i j}=\varrho\left(s_j-s_i\right) \]

\[ \begin{gathered} \boldsymbol{d}_i=\varrho(v t) \\ \varrho(x)=\operatorname{sgn}(x) \sqrt{|x|} \end{gathered} \]

其中 $\operatorname{sgn}()$ 是符号函数。velocyto 中还实现了其他形式的 $\varrho$ 变换，包括恒等和基于对数的函数。过渡矩阵进行了行归一化，以确保 $\sum_j \boldsymbol{P}_{i j}=1$。然后使用过渡概率 $P_{i j}$ 作为权重来计算单位位移向量的线性组合。给定一个由一组向量描述的细胞的 $\mathrm{n}$ 个位置的嵌入

\[ \boldsymbol{X}=\left[x_1, x_2, \ldots, x_{n-1}, x_n\right] \]

计算细胞的预测速度位移为：

\[ \Delta x_i=\sum_j\left(P_{i j}-\frac{1}{n}\right) \frac{\left(x_j-x_i\right)}{\left\|x_j-x_i\right\|} \]

其中减去 $1 / n$ 是为了纠正嵌入中点密度非均匀性的估计。

对于大型数据集，单个细胞速度箭头的可视化不实用。在这种情况下，我们可视化了在规则网格上评估的局部群体速度的矢量场。网格矢量场是通过对网格点周围细胞的速度向量应用高斯核平滑来估计的：

\[ \Delta x_{\text {grid }}=\sum_i K_\sigma\left(x_{\text {grid }}, x_i\right) \Delta x_i \]

其中核函数 $K_\sigma$ 定义为：

\[ K_\sigma(a, b)=\exp \left(\frac{-\|a-b\|^2}{2 \sigma^2}\right) \]

网格的大小（网格点数）根据图形的视觉规模选择。

扩散起点和终点建模（图 3）

为了找到对应于分化起点（如早期神经前体细胞）和终点（如神经元和胶质细胞）的细胞集，我们使用了一个马尔可夫过程，其转移概率矩阵 $\boldsymbol{T}$ 中的每个条目定义如下：

\[ \boldsymbol{T}_{i j}=p \boldsymbol{W}_{i j}+(1-p) \boldsymbol{D}_{i j} \]

其中，$\mathbf{W}$ （经行和归一化后）对应于局部布朗运动分量：

\[ \boldsymbol{W}_{i j}=K_{\sigma_W}\left(\boldsymbol{x}_i, \boldsymbol{x}_j\right) \]

而 $\mathrm{D}$ （经行和归一化后）代表局部速度驱动的漂移：

\[ D_{i j}=P_{i j} K_{\sigma_D}\left(\boldsymbol{x}_i, \boldsymbol{x}_j\right) \]

高斯核 $K_{\sigma_D}$ 被用来使扩散过程在嵌入上逐渐且局部地进行。$\mathrm{p}<0.5$ 是我们设置为 0.2 的混合比例。此外，为了避免局部点密度对结果的影响，我们通过选择均匀网格的最近邻进行了数据集的降采样。$\sigma_D$ 被设置为相邻点之间的平均距离，$\sigma_W=\sigma_D / 2$。逆向扩散（即逆向速度偏见的扩散）通过转置和行归一化转移概率矩阵 $\boldsymbol{T}$ 来进行。在扩散的两个方向上，我们都从均匀分布开始，并执行了 2500 次迭代。

基因相对估计 RNA 速度的实现细节

在基本的速度估算方案中，$o$ 被认为是在 $s=0$ 时各细胞中 $u$ 的平均值。对于最小二乘拟合，细胞特定的回归权重 $w$ 被设定为 $e^4+s^4$。请注意，使用分位数拟合、跨度读取基于拟合或基因 $k \mathrm{NN}$ 池化时，$o$ 和 $\gamma$ 的拟合使用了不同的逻辑。为了在低计数时提高稳定性，$\hat{u}$ 还额外计算了添加或减去一个伪计数，并报告了一个最小幅度速度 $v$。

为了处理大多数观察细胞处于非稳态的情况，我们使用表达值的极端分位数来拟合 $\gamma$ 系数和偏移 $o$。具体来说，线性模型 $u \sim \gamma * s+o$ 被用来拟合斜率和截距（$\gamma$ 和 $o$）系数，限制了一组细胞的 $s$ 值在该基因的顶部和底部 5％内（对于较大的数据集，如小鼠 BM，使用了 2％）。没有使用回归权重。velocyto 包还实现了一个“对角线分位数”选项，其中极端分位数不仅基于剪接表达量，还基于剪接和未剪接表达量的归一化总和 $(x=s / S+u / U)$，其中 $U$ 和 $S$ 分别是该基因的最大未剪接和剪接表达量。

基因 kNN 池化

通过池化 $k$ 个相关性最高的基因的计数来实现基因池化。基因相关性通过对 $\log (s+1)$ 值进行皮尔逊线性相关距离评估。结果矩阵代表了元基因的计数。然后在池化的基因计数上进行了斜率和偏移估算。然后根据假设，观察到的 $v$ 与预期的（在稳态下）未剪接信号比率在共同调控的基因之间应该是相似的，因此也适用于池化的基因计数，评估原始基因的速度。对于给定基因和给定细胞，观察到的未剪接计数与预期的对数比率被计算为 $m=\log _2\left(\frac{u}{\hat{\gamma} s+\hat{\sigma}}\right)$，其中 $\hat{\gamma}$ 和 $\hat{o}$ 是使用元基因矩阵获得的斜率和偏移估计。然后通过取所有 $s>0$ 的细胞中的 $2^{\log _2(\tilde{u} / s)-m}$ 的平均值来估计基因特异性的 $\gamma$。在假设 $u$ 恒定的情况下（模型 II），$\Delta s(t)$ 然后被估计为 $\Delta s(t)=(s+\epsilon)\left[e^{-\gamma t}\left(1-2^m\right)+2^m\right]-s$，其中 $\epsilon=10^{-4}$。

基于结构的 RNA 速度估算（扩展数据图 4）

基于结构的模型从使用上述基因相对模型获得的初始估计 $\left(\gamma_r\right)$ 开始。然后，它继续拟合一个广义加性模型 (gam)，以预测基于一组基因结构参数（如外显子数、总内含子长度或预测的内部引物位点数）的基因特异性 $\gamma$ 值。这个模型预测的 $\gamma$ 值然后被转换为未剪接计数 $\mathrm{M}$ 值（观察到的与稳态下预期的未剪接计数比率的对数）。与 $\gamma$ 估计不同，$\mathrm{M}$ 值可以直接在基因之间进行比较，我们预期共同调控的基因在上调和下调过程中显示相似的 $M$ 值。因此，通过在紧密相关的基因之间应用修剪均值程序进一步完善了 $\mathrm{M}$ 值，这些调整后的 M 值最终用于外推细胞的未来表达状态。

该分析仅考虑具有多于一个注释外显子（$\left.n_e>2\right)$ 的基因，外显子总长度 $l_e$ 超过 $500 \mathrm{bp}$，内含子总长度 $l_i$ 超过 $3 \mathrm{kbp}$。然后构建了一个全局广义加性模型来拟合 $\gamma_r$ 与基因的结构参数和表达量之间的依赖关系：

\[ \gamma_r \sim K_2\left(s, l_i\right)+K_1\left(\log _{10}\left(\frac{l_i+1}{l_e+1}\right)\right)+K_1\left(n_e\right)+K_1\left(n_c\right)+K_1\left(n_d\right) \]

其中 $K_1$ 和 $K_2$ 分别表示 1D 和 2D 的局部平滑核，由 $\mathrm{mgcv} \mathrm{R}$ 包实现。此处，$s$ 表示基因的剪接表达量，$n_e$ 是基因中表达的外显子数。$n_c$ 和 $n_d$ 分别表示一致和不一致的内部引物位点数（有关内部引物位点的详细信息，请参见扩展数据图 1）。模型的拟合采用了数据集中每个基因的总剪接计数的平方根作为权重。拟合过程还排除了未剪接计数过多的基因（可能由于未注释的非编码转录本）。为此，使用带有正态分布和对数链接的广义线性模型对总未剪接计数进行了建模，$\sum_{\text {cells }} u \sim \sum_{\text {cells }} s+l_i / l_e$，并在拟合模型时排除了皮尔逊偏差超过 3 的基因。

然后使用全局模型预测通过上述结构参数阈值的所有基因的基于结构的稳态 $\gamma\left(\gamma_s\right)$。然后使用 $\gamma_s$ 来估计观察到的与预期的未剪接计数的对数比率为 $m_s=\log _2\left(\frac{u}{\gamma_s s+o_r}\right)$，其中 $o_r$ 是如基因相对模型所述确定的基因特异性偏移。由于我们预期单个基因的 $m_s$ 估计会有噪声，因此下一步使用 $k$ 最近的基因来稳定每个基因的 $m$ 估计。具体来说，对于给定的基因 $g$，$m$ 被估计为与基因 $g$ 在整个数据集中最相关的 $k$ 个基因的 $m_s$ 值的修剪均值。默认使用 $k=15$，并修剪顶部和底部的 5 个基因。然后使用这些稳健的 $m$ 估计来估计 RNA 速度，如“基因 kNN 池化”中所述。

新陈代谢标记（扩展数据图 2）

我们按照文献[22]的描述，使用 4-硫尿嘧啶对 Hek293 细胞进行了新陈代谢标记，但没有进行片段化处理（4sU 测序），然后使用 STRT 技术[23]准备了批量 RNA 样本进行测序。我们将细胞在 5 分钟、15 分钟和 30 分钟的条件下各自孵育了两份，并包括了一个不进行拉取的对照，代表稳态表达状态。重要的是，STRT 是基于寡聚 dT 引物的单细胞 RNA 测序协议，因此应该可以代表旨在检测多聚 A+ RNA 的协议。我们之前估计交叉污染（在标记 RNA 中发现的非标记 RNA 的比例）约为 0.5%，尽管由于 4sU 测序的内部对照未进行聚腺苷酸化，我们无法在此直接测量。我们针对每个条件分析了两个独立的生物样本，每个样本进行了两次技术重复（反转录）。

数据使用标准的 velocyto 计数管道进行分析，选择了“-b8”选项。选择满足以下条件的基因：（1）在所有对照样本中检测到剪接分子；（2）在至少 75%的拉取样本中和至少两个对照样本中检测到未剪接分子；（3）在高未剪接表达的拉取样本中，未剪接分子的水平至少是对照样本的两倍；（4）剪接分数的变异系数低于通过使用剪接量作为预测因子的线性模型所预测的（拟合残差高于第 10 百分位）；（5）通过方差分析确定的时间依赖趋势具有显著性（p<0.15）。对基因进行了因子分析，并且使用高斯混合模型在两个因子的空间中对基因进行了聚类。在获得的两个簇中，较小的一个展示了不符合简单转录模型的不协调特征，因此没有进一步处理。对于剩余的基因，我们考虑了剪接分子的观察比例 $\frac{s}{s+u}$。通过最小二乘法拟合以下方程得出 beta 和 gamma 参数，该方程源自时间独立率模型的解（注意计算比例 $s /(s+u)$ 时可以简化 alpha）：

\[ \frac{s}{s+u}=f(\beta, \gamma, t)=\frac{1}{\left(\frac{\beta+\gamma}{\beta}+\frac{\left(-e^{t \beta}+e^{t \gamma}\right) \gamma}{e^{t \beta} \beta-e^{t \gamma} \gamma+e^{t(\beta+\gamma)}(\gamma-\beta)}\right)} \]

对于渐进增加系统的时间常数 $\tau$，定义为达到其平衡值的 $1-\frac{1}{e} \cong 0.632$ 的比例所需的时间，剪接分数的极限是 $\lim _{t \rightarrow \infty} \frac{s}{s+u}=\frac{\beta}{\beta+\gamma}$；因此，通过数值解以下方程获得 $\tau$ 的值：

$$ \frac{1}{\left(\frac{\beta+\gamma}{\beta}+\frac{\left(-e^{\tau \beta}+e^{\tau \gamma}\right) \gamma}{e^{\tau \beta} \beta-e^{\tau \gamma} \gamma+e^{\tau(\beta+\gamma)}(\gamma-\beta)}\right)}-\frac{\beta\left(1

-\frac{1}{e}\right)}{\beta+\gamma}=0 $$