Spatial transition tensor of single cells
摘要¶
空间转录组学和信使 RNA 剪接编码了细胞状态和转变的广泛时空信息。当前的谱系推断方法要么缺乏状态转变的空间动态,要么无法捕捉与多个细胞状态和转变路径相关的不同动态。在此,我们提出了空间转变张量(STT),这是一种通过多尺度动态模型使用信使 RNA 剪接和空间转录组学来表征空间中多稳态的方法。通过学习四维转变张量和空间约束的随机游走,STT 通过细胞之间的短时间局部张量流线和吸引子之间的长期转变路径重构了细胞状态特异性动态和空间状态转变。在多种技术下对上皮 - 间充质转变、血液发育、空间分辨的小鼠大脑和鸡心脏发育等多个转录组数据集的基准测试和应用表明,STT 能够恢复现有方法未能发现的细胞状态特异性动态及其相关基因。总体而言,STT 提供了单细胞转录组数据在多个时空尺度上的一致多尺度描述。
主文¶
单细胞基因表达谱技术的进步为解析细胞命运决策提供了前所未有的分辨率。类似性或低维流形上的距离等指标应用于单细胞 RNA 测序(scRNA-seq)数据,以推断伪时间排序 1,2、网络抽象 3 或细胞随机游走分析 4,5 等动态特性。利用未剪接和已剪接计数,RNA 速度方法 6,7 显式地建模信使 RNA(mRNA)的动态,将细胞未来的剪接状态投射到 scRNA-seq 数据上,以揭示细胞命运决定的方向性 8,并改进轨迹推断 9,10,11、低维嵌入 12,13 和基因调控网络推断 14,15。
空间转录组学在单个细胞或小组细胞的点上测量额外的空间信息,允许分析空间中的异质细胞状态 16,17。为了推断空间转录组学中的时间动态,SpaceFlow18 使用邻近信息约束细胞嵌入和伪时间排序以实现空间一致性。SIRV19 开发了一种空间解析 RNA 速度方法,通过使用参考 scRNA-seq 数据来改进未剪接和已剪接 mRNA 的估计,以丰富空间转录组学基因表达矩阵。
尽管 RNA 速度已被广泛使用,但在重建稳健的时空动态方面仍然存在基本挑战 20。例如,当前模型无法捕捉复杂空间组织中的多谱系或多个亚稳态 21,22,23,因为由于非线性基因调控或多细胞信号传导,剪接和未剪接的转录水平可能会出现偏离。此外,mRNA 剪接的时间尺度在几分钟或几小时内 24,25,在此期间,当前的 RNA 速度模型会收敛到一个全局平衡,而细胞状态的转变可能跨越数天到数周(例如,在造血过程中 8,20,25)。尽管可以使用细胞特异性的基因表达速率来适应连续的细胞命运承诺过程 25,26,但需要额外的测量,如代谢标记 27,28,29,这在空间转录组学中很难获得。最后,当前主要的 RNA 速度方法仅关注剪接计数的速度,忽略了与基因调控密切相关的未剪接计数的速度 15,这可能提供关于某些细胞状态“吸引力”的进一步信息。
多尺度细胞吸引子理论 30,31,32,33,34,35 为跨不同时间尺度和分辨率建模动态提供了一种自然工具,并考虑到多稳定状态。在这样的理论中,基因表达的时间变化及其相互调控被建模为一组微分方程组成的动态系统。稳定的细胞类型对应于在基因调控的轻微扰动下动态系统的多个局部稳定固定点(即多稳定状态),其中表达的细胞状态被“困住”,而高可塑性的过渡细胞被建模为系统的“鞍点”,使细胞可以通过某些方向进行状态转换。使用这种方法,MuTrans5 在不同尺度上粗粒化 scRNA-seq 数据以识别吸引子和鞍点,允许描述细胞在吸引子周围的短时间波动,同时捕捉细胞在多个吸引子之间的长时间尺度转换,鞍点在其中。MuTrans 中的高斯核将其范围限制在平衡和遍历系统 4,5。对于非平衡系统,使用 RNA 速度作为输入,CellRank8 使用速度核构建细胞随机游走,随后进行粗粒化分析,Dynamo25 通过使用连续函数拟合离散 RNA 速度进行吸引几何和转换分析。然而,在这些方法中,线性 RNA 速度模型与数据中继承的多稳定吸引子的存在不兼容,导致转变速度和下游分析之间的不一致。此外,这些方法不能直接用于空间转录组数据。
在此,我们提出了一种空间转变张量(STT)方法,使用未剪接和已剪接 mRNA 计数在空间转录组数据中重建细胞吸引子,以允许量化空间吸引子之间的转换路径以及单个过渡细胞的分析。与具有一个全局平衡的线性 RNA 速度模型不同(图 1a),STT 假设在联合未剪接(U)- 剪接(S)计数空间中存在多个吸引子,细胞在吸引子盆地之间进行转换(图 1a,b)。构建跨细胞、基因、剪接状态和吸引子的四维转变张量,每个吸引子盆地都关联有吸引子特异性量(图 1b)。通过迭代细化张量估计并分解张量引导和空间约束的细胞随机游走(图 1c–e,g),STT 连接了局部基因表达和剪接动态与吸引子之间的全局状态转换之间的尺度。此外,STT 对与多稳定表达模式最相关的基因进行排序,并分类具有类似 STT 特性的途径(图 1g)。通过研究非空间和空间数据集,我们展示了 STT 在揭示细胞多稳定吸引子及其在不同时空尺度上发生的转换特性方面的独特能力。

a. 比较 RNA 速度(线性和单一平衡)与 STT 张量模型(多稳态和多个吸引子)。 b. 通过平均细胞在不同吸引子中的归属,定义过渡张量和诱导的 RNA 速度。 c–f. STT 的工作流程。 c. 输入的 U 和 S 计数矩阵。 d,e. 过渡张量的动力学参数估计(d)与动力学分解和粗粒化(e)之间的迭代方案。 f. STT 的输出结果 g. 使用 STT 分析空间转录组学数据,其中基于空间细胞坐标的空间相似核与张量诱导和基因表达诱导的核相结合,以推断细胞在吸引子中的归属。在路径相似性图中,Dim.表示降维后的坐标。
结果¶
STT 概述¶
STT 的输入包括单细胞基因表达矩阵的 \(S\) 和 \(U\) 计数(图 1c),以及细胞注释(或归属),这些作为细胞状态的初始猜测。此外,还需要每个细胞(或位置)的空间坐标,以用于空间转录组数据。通过参数估计和动力学分解之间的迭代,STT 构建了一个以吸引子为单位的速度张量,称为过渡张量,其形状为 \(\mathbb{R}^{N_{\mathrm{C}} \times 2 \times K \times N_{\mathrm{G}}}\),其中 \(N_{\mathrm{C}}\) 表示细胞数量,\(N_{\mathrm{G}}\) 表示基因数量,\(K\) 表示吸引子数量。张量动力学的其他量,包括细胞在吸引子中的归属、过渡概率和过渡路径,随后在此构建中获得(方法部分)。
STT 使用以下基因表达和剪接动力学的随机模型
其中 \(U_i\) 和 \(S_i\) 分别是基因 \(i\) 的未剪接和剪接计数。非线性函数 \(f_i\) \(\left(t, S_1, \ldots, S_{N_{\mathrm{G}}}\right)\) 模拟了其他基因如何调控基因 \(i\) 的生产速率。该系统可以具有多个固定点或吸引子,代表不同的细胞状态。参数 \(\beta_i\) 表示 mRNA 剪接速率,\(\gamma_i\) 是剪接 mRNA 降解速率。独立的维纳过程项 \(W_{i, t}\) 和 \(Z_{i, t}\) 代表基因表达中的噪声。这种随机性可能会在比剪接动力学更长的时间尺度上诱导多稳态吸引子之间的噪声诱导细胞状态转变。
当大多数细胞位于对应不同细胞状态的多个吸引子盆地内,只有少数细胞跨越鞍点进行过渡(这是对细胞分布的自然假设)时,未剪接 mRNA 的生产项可以展开并近似为其线性展开,从而引入吸引子相关的 mRNA 转录速率(图 1d 和方法部分)。这种展开允许对参数进行稳健估计,并初始化每个细胞的吸引子速度分配,我们称之为过渡张量(图 1d 和方法部分)。
通过构建内积速度核(图 1d,方法部分和补充说明 1),张量提供了一种与连续随机微分方程(SDE)渐近一致的细胞随机游走描述(即方程(1))。结合基因表达相似性的高斯核和细胞空间坐标(图 1g 和方法部分),构建的细胞随机游走为每个吸引子中的细胞提供了一致的速度、过渡方向和相似的基因表达。此外,构建的随机游走鼓励细胞更可能向物理空间中其他空间上相邻的细胞过渡。通过在吸引子水平上粗粒化和分解随机游走,然后获得细胞在不同吸引子中的归属函数(图 1e 和方法部分)。在张量模型构建和随机游走分解之间的每次迭代中,更新的归属函数通过引入吸引子不确定性来改进方程(1)中的参数估计(方法部分)。在迭代过程中,识别出在 U-S 空间中与吸引子特性最一致的基因(方法部分)。包括一个监控模块,具有正则化和早停策略,通过用户控制可以提高迭代的稳健性(方法部分)。最后,将描述吸引子细节的张量流线以及描绘长时间过渡的粗粒化过渡路径投影在低维动力学流形上,以显示细胞状态的转变(图 1f 和方法部分)。
多稳态细胞状态恢复的 STT 基准测试¶
我们首先应用 STT 分析了基于模拟多稳态系统的两个合成数据集。在双稳态开关电路中,STT 中吸引子平均速度的流线比 RNA 速度和其他方法的流线展示了更清晰的两个吸引子结构(图 2a 和补充图 1)。尽管由 scVelo7 和 UniTVelo36 计算的 RNA 速度流线倾向于从吸引子位置发散,STT 流线则向吸引子收敛,从而提供了更易解释的开关景观表示(图 2a 和补充图 1)。此外,STT 计算出一个熵值来区分固定点附近的稳定细胞和跨越鞍点的过渡细胞(补充图 1)。如流线显示的过渡张量的两个组成部分所示(补充图 1),只有当未剪接和剪接的数量同时考虑时,才能揭示出吸引子盆地。尽管剪接张量与标准的 RNA 速度一致(图 2a),显示了吸引子之间的过渡,未剪接张量则自然引入了一种“吸引力”,将细胞“拉”向每个吸引子的中心,而与 cellDancer37 的流线相比,后者细胞被吸引到吸引子内的“端点”(补充图 1)。未剪接计数为 STT 提供了一个对细胞状态吸引子的“吸引”水平的测量。为了进一步验证 STT 的准确性,我们比较了 STT 未剪接或剪接张量成分与模型的真实速度之间的余弦相似性,发现 STT 在估计剪接和未剪接速度方面均排名靠前(图 2b)。此外,STT 在对数据集进行子抽样时表现出了良好的稳健性(补充图 1)。
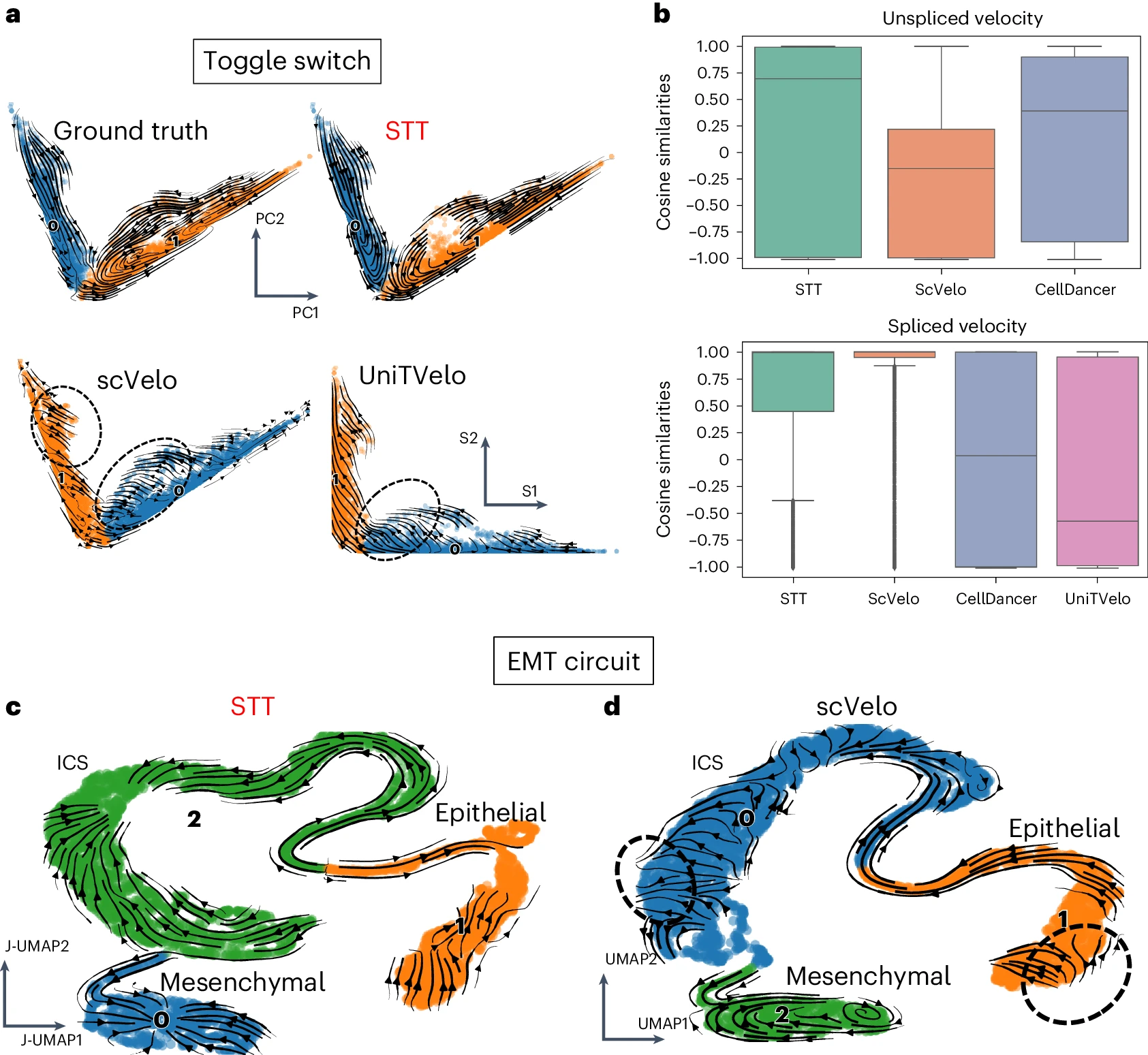
a. 比较 STT 与其他方法在开关数据集上的流线。STT 中的细胞根据吸引子进行着色,而 scVelo 和 UniTVelo 中的细胞则根据 Leiden 聚类结果进行着色。STT、scVelo 和真实结果嵌入在联合剪接和未剪接计数的 PCA 中,UniTVelo 的结果绘制在剪接计数的坐标上。 b. 计算速度与真实值在不同方法中余弦相似性的所有细胞(n = 10,010)的箱线图。中央箱体表示四分位范围,从第 25 百分位数(下边界)到第 75 百分位数(上边界),箱体内的水平线表示中位数(第 50 百分位数)。须线延伸到下四分位数和上四分位数 1.5 倍四分位范围内的值。点表示离群值。 c,d. 比较 STT 与其他方法在合成 EMT 电路数据集上的流线。 c. 细胞根据 STT 的吸引子分配进行着色,低维嵌入是基于联合剪接和未剪接计数的 UMAP。流线使用吸引子上的平均速度进行可视化。 d. 细胞根据 Leiden 聚类结果进行着色,低维嵌入是仅基于剪接计数的 UMAP。流线使用 RNA 速度进行可视化。
接下来,我们分析了在上皮 - 间质转化(EMT)过程中模拟的基因调控电路,其中在某些参数范围内,可能共存三个吸引子,分别表示上皮状态(E)、间质状态(M)和中间细胞状态(ICS)(方法部分)。与 scVelo 计算的 RNA 速度相比(图 2),STT 平均速度(图 2c)清晰地恢复了这三个吸引子。总体而言,STT 能够重建单细胞基因表达数据集中复杂的多稳态细节。
STT 突出了命运决策中的 iCS¶
接下来,我们分析了人类肺 A549 细胞系在 EMT 诱导实验中的 scRNA-seq 数据,包括从 TGFB1 处理后的前 7 天收集的一系列时间点快照。STT 识别出三个吸引子,分别为 E、ICS 和 M,与数据收集时间点的顺序一致(图 3a、b 和补充图 2)。此外,ICS 吸引子附近的细胞,主要在诱导后 8 小时或 1 天收集(图 3b),具有较高的熵值(图 3c),表明这种状态比上皮(第 0 天和 8 小时)和间质(第 3 天后)状态更具可塑性。这与在癌症中提出的中间上皮和/或间质状态的表型可塑性很好地吻合。
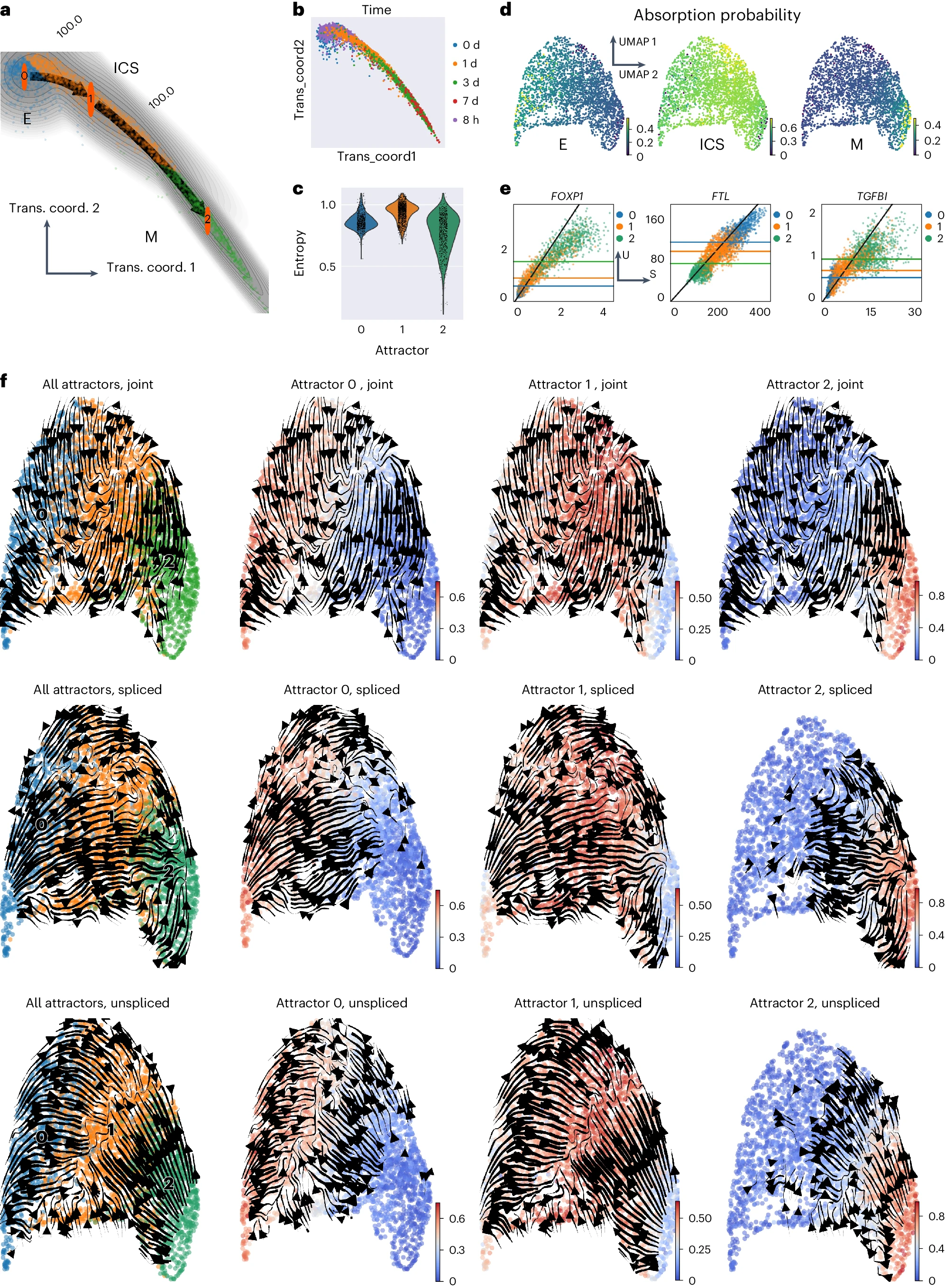
a. EMT 的全局过渡路径分析。细胞嵌入在构建的动力学流形的过渡坐标(trans. coord.)中,数字表示过渡流的比例。细胞按 STT 吸引子着色。 b. 过渡坐标中的细胞按收集时间点着色 c. 不同吸引子中细胞归属熵的小提琴图。 d. 使用多稳态核诱导的随机游走计算的细胞吸收到不同吸引子的吸收概率。 e. 在 EMT 中与吸引子的多稳态一致的主要基因。 f. 各种过渡张量成分的流线,包括吸引子平均张量和吸引子特定张量。低维嵌入是剪接和未剪接计数的 UMAP。左图中,细胞按吸引子分配着色。右图中,细胞按其在每个吸引子中的归属着色,仅显示归属度大于 0.2 的细胞的张量。
使用过渡向量预测在上皮 - 间质景观中连接吸引子的过渡路径,我们发现从 E 到 M 的过渡概率流量始终通过 ICS(图 3a)。换句话说,经历 EMT 的上皮细胞不会直接转换为间质状态,而是首先获得中间特征。未剪接和剪接计数通常表现出吸引子的多稳态性(图 3e 和补充图 2、3)。具有高多稳态评分的基因在各种吸引子中的未剪接和剪接计数中表现出不同的表达水平,并在 E-ICS-M 过渡过程中显示出逐渐变化。虽然像 ITGA11 这样高排名的多稳态基因在差异基因表达分析中并未显著地作为吸引子的最高评分标志基因检测到(补充图 3),但它们在促进 EMT 过渡和肿瘤进展中被发现具有重要作用。尽管剪接动力学的张量流线显示了从 E 到 M 通过 ICS 的总体方向,这也与 UniTVelo 的结果一致(补充图 2),但未剪接计数以及 STT 和 cellDancer 在联合 U-S 空间中预测的基因表达动力学都表明细胞在 EMT 期间被“吸引”到 ICS 盆地(图 3f 和补充图 2)。这也与基于张量诱导的多稳态核的 CellRank 吸收概率分析一致(图 3d)。总之,张量成分及其全局过渡路径分析突出了 ICS 作为 EMT 期间的一个独特吸引子盆地,作为中心状态。
此外,我们将 STT 应用于血液和胰腺发育数据集,发现其能够解决复杂的状态过渡,其多稳态张量核与 CellRank 分析一致(补充图 4 和图 5)。
STT 识别空间吸引子和路径相似性¶
我们接下来将 STT 应用于小鼠脑发育的 HybISS 空间数据集。为了丰富未剪接和剪接计数以便更好地进行张量估计,我们使用 SIRV19 算法推算了 E10 和 E11 在 40μm 处的原始空间数据切片中的一个。与仅基于细胞相似性的聚类相比(补充图 6),STT 识别出与不同细胞状态的空间位置一致的吸引子(图 4a)和原始出版物中的脑区注释(图 4b):同一吸引子内的细胞往往具有相似的空间坐标,并属于相同的区域。此外,发现细胞分配对空间扩散核的权重(补充图 6)、吸引子初始化(补充图 7)、多稳态基因过滤(补充图 8)和吸引子数量(补充图 9)具有稳健性。前脑和后脑吸引子的局部过渡张量(图 4c)与 UniTVelo 分析一致(补充图 6)。
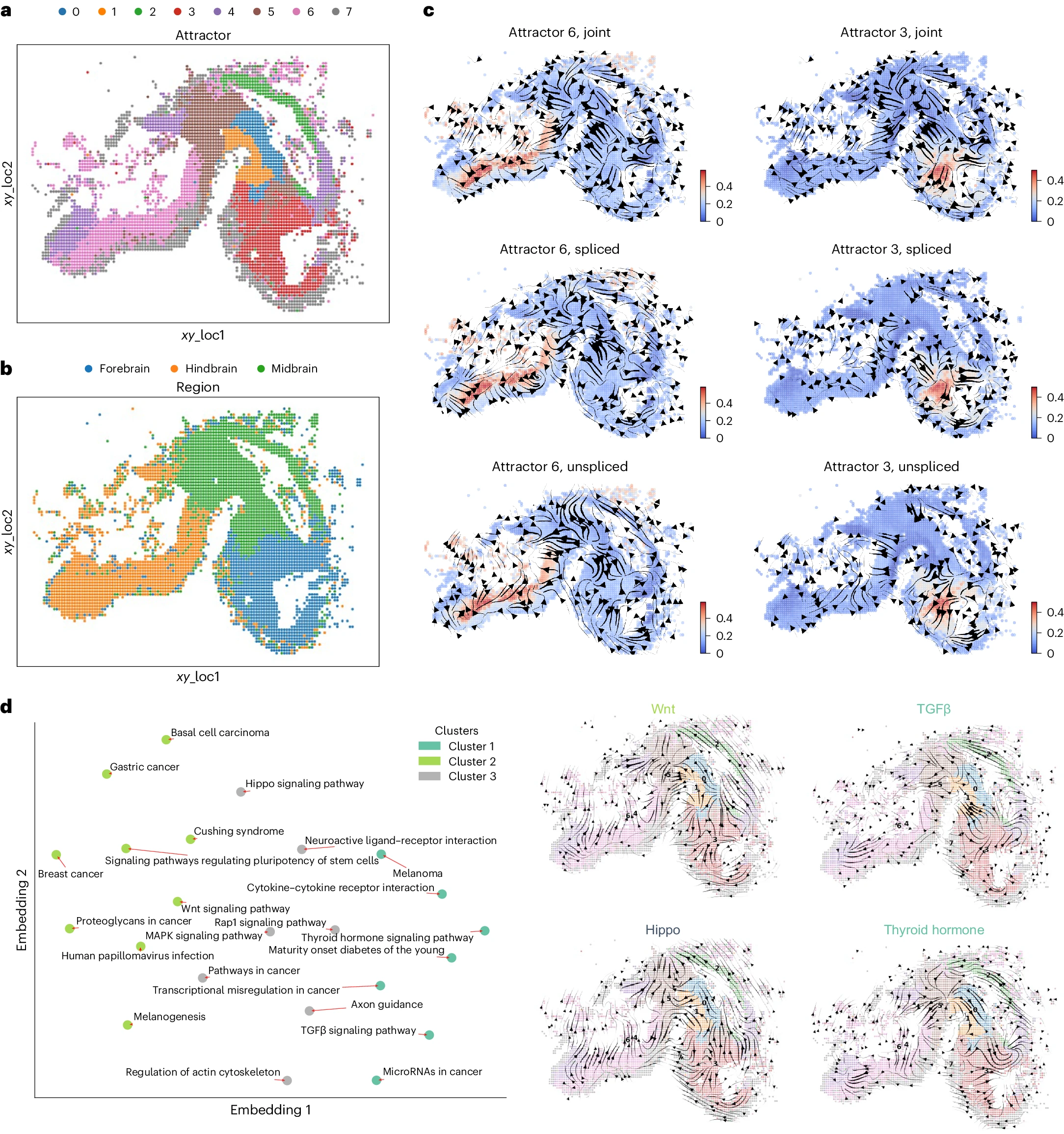
a,b. 数据的空间注释和 STT 检测到的吸引子,细胞按不同类别着色:吸引子(a)和区域(b)。 c. 在特定吸引子 6 和 3 中的局部过渡张量流线。细胞按其在相应吸引子中的归属着色。 d. 不同 KEGG 通路之间的过渡张量相似性。左侧显示了小鼠脑发育空间动态中相似生物通路的聚类二维嵌入,其中来自各种通路的平均张量流线展示了不同的过渡动态。具有至少三个与 STT 多稳态基因重叠的基因的通路显示在低维嵌入中。右侧显示了来自不同聚类的特定通路的流线,细胞嵌入在空间坐标中。
为了评估张量流线的生物学意义,我们进行了通路特异性分析,以评估与细胞状态转变和通路调控相关的功能(图 4d)。我们使用了京都基因与基因组百科全书(KEGG)知识数据库,并基于多稳态基因的张量相关性计算各通路之间的相似性(方法部分)。确实,通路特异性张量展示了不同的吸引子动态。基于张量相关性的潜在嵌入和通路聚类(图 4d)揭示了发育过程中通路之间空间状态转变的功能相似性。已知在胚胎发生过程中存在交叉对话并协同作用的 TGF-beta 和 WNT 通路在潜在嵌入中来自不同的聚类,并且它们的张量流线方向相反,特别是在中脑和前脑吸引子中(图 4d)。在脑发育中两个其他重要的通路,Hippo 和甲状腺激素信号通路,也来自不同的通路张量聚类,显示出在中脑和前脑区域相反的流线(图 4d)。总体而言,STT 提供了细胞状态的空间组织和在发育过程中调控状态转变的通路之间关系的动态信息。
STT 揭示了鸡心的空间吸引子和谱系¶
我们将 STT 应用于通过 10X Visium 技术测量的空间解析鸡心数据。我们的分析重点是数据集在第 14 天的最后时间点,此时四腔室的发育已经完成,心脏发生和明确的空间边界已经完成。
使用 SIRV 推测的未剪接和剪接计数,STT 识别出五个空间解析的吸引子(图 5a 和补充图 10)。其中,吸引子 2 与原始研究中的“瓣膜”区域一致,主要由成纤维细胞组成(图 5a,b,d,e)。吸引子 0 主要由来自右心室区域的细胞组成(图 5e)。吸引子 1 主要位于“心房”区域(图 5e),由红细胞组成。而其余的吸引子(3、4)分布在几个连接区域,它们都包括注释表型为心肌细胞的细胞(图 5a,b,d,e)。动力流形揭示了这些离散吸引子(图 5c)与不同的细胞谱系有关。吸引子 1 和 2 包含空间定位的成纤维细胞和红细胞谱系,都展示了张量流线中的“吸引力”(图 5f)。相比之下,吸引子 3 和 4(均含有心肌细胞)内的张量流线表明它们在空间上的短暂性,并显示出向心房区域过渡的趋势,这在未剪接成分的“吸引”中也可以观察到。这可能部分解释了心房中另一组心肌细胞的存在(图 5b,d)。总体而言,与空间区域或细胞类型注释的一致性表明 STT 有能力解析空间解析的吸引子。
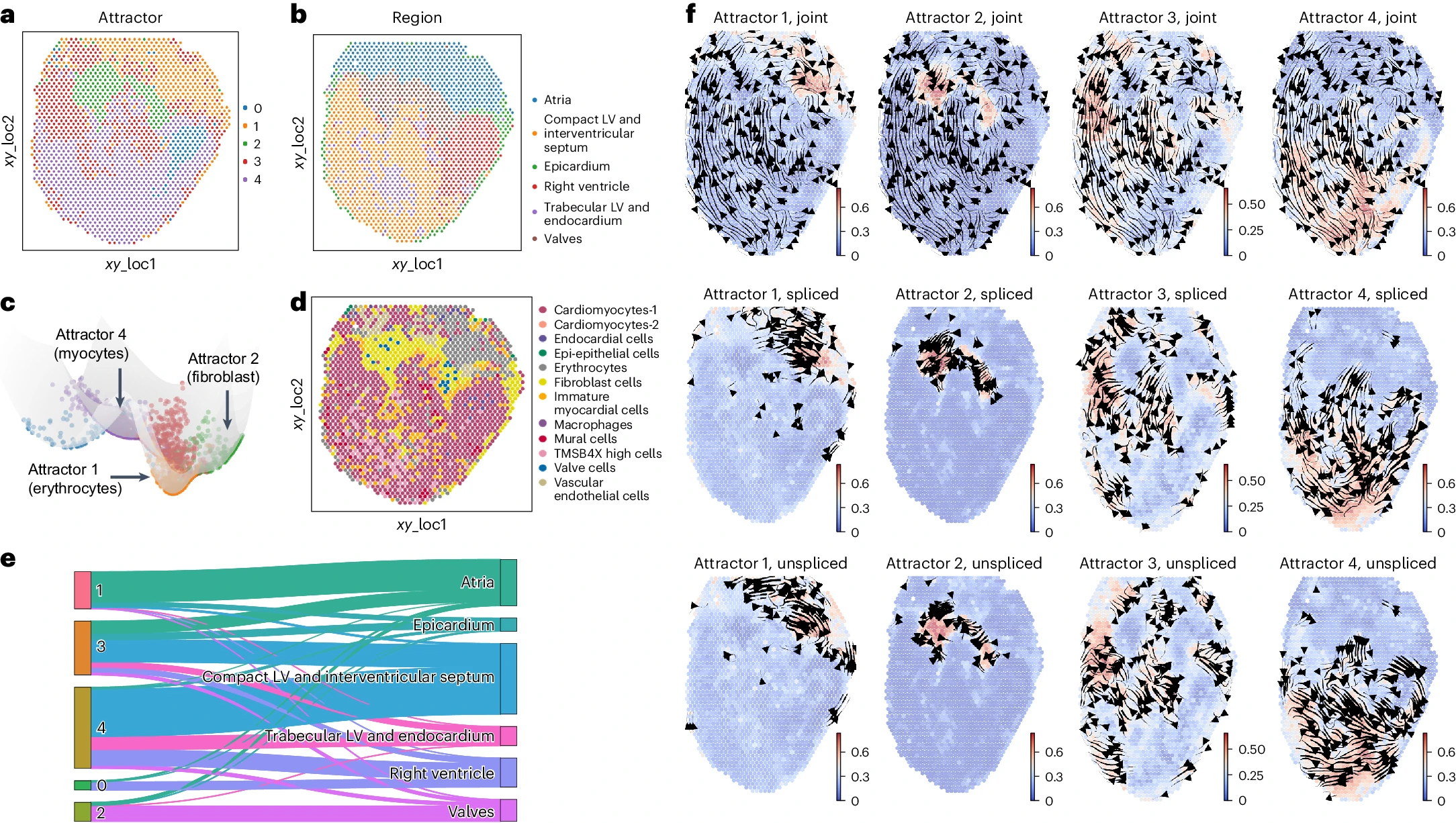
a,b. 分析数据的空间点,其中空间点按 STT 检测到的吸引子区域(a)或原始研究中的注释(b)进行着色。 c. 构建的数据动力学景观,其中空间点按吸引子进行着色。 d. 按原始研究中的细胞类型注释进行着色的空间点。 e. Sankey 图显示 STT 吸引子(左)与空间区域注释(右)之间的关系。链接的宽度表示同时共享连接的吸引子标签和区域注释标签的细胞数量。 f. 特定吸引子 1、2、3 和 4 中的局部过渡张量流线。细胞按其在相应吸引子中的归属进行着色。
STT 阐明了区域特异性的空间吸引子及其稳定性¶
我们接下来分析了使用 60 大小的 bin 处理的高分辨率 Stereo-seq 小鼠成年冠状脑半球数据集,该数据集揭示了具有各种生物功能的神经细胞的复杂区域。直接应用 STT 显示了多个区域特异性的空间吸引子,这些吸引子与脑区的功能注释非常一致(图 6a,b)。张量的收敛流线(图 6c)表明,基因表达动力学的多稳态性在诸如皮层子区(吸引子 4)和纹状体背侧区域(吸引子 10)等区域得到了很好的保持。张量的所有成分在丘脑区域(吸引子 8)向外流动(图 6c),表明其相对较高的可塑性。基于它们的张量动力学的通路嵌入显示,已知的相互作用通路如 cGMP-PKG 和钙信号通路共享相似的张量动力学(图 6d)。它还表明 cGMP-PKG 不同于催产素通路,其中流线表明主要差异发生在杏仁核区域(图 6d)。总体而言,结果表明 STT 能够通过吸引子分析发现空间区域并量化其稳定性,即使在成熟组织中也是如此。
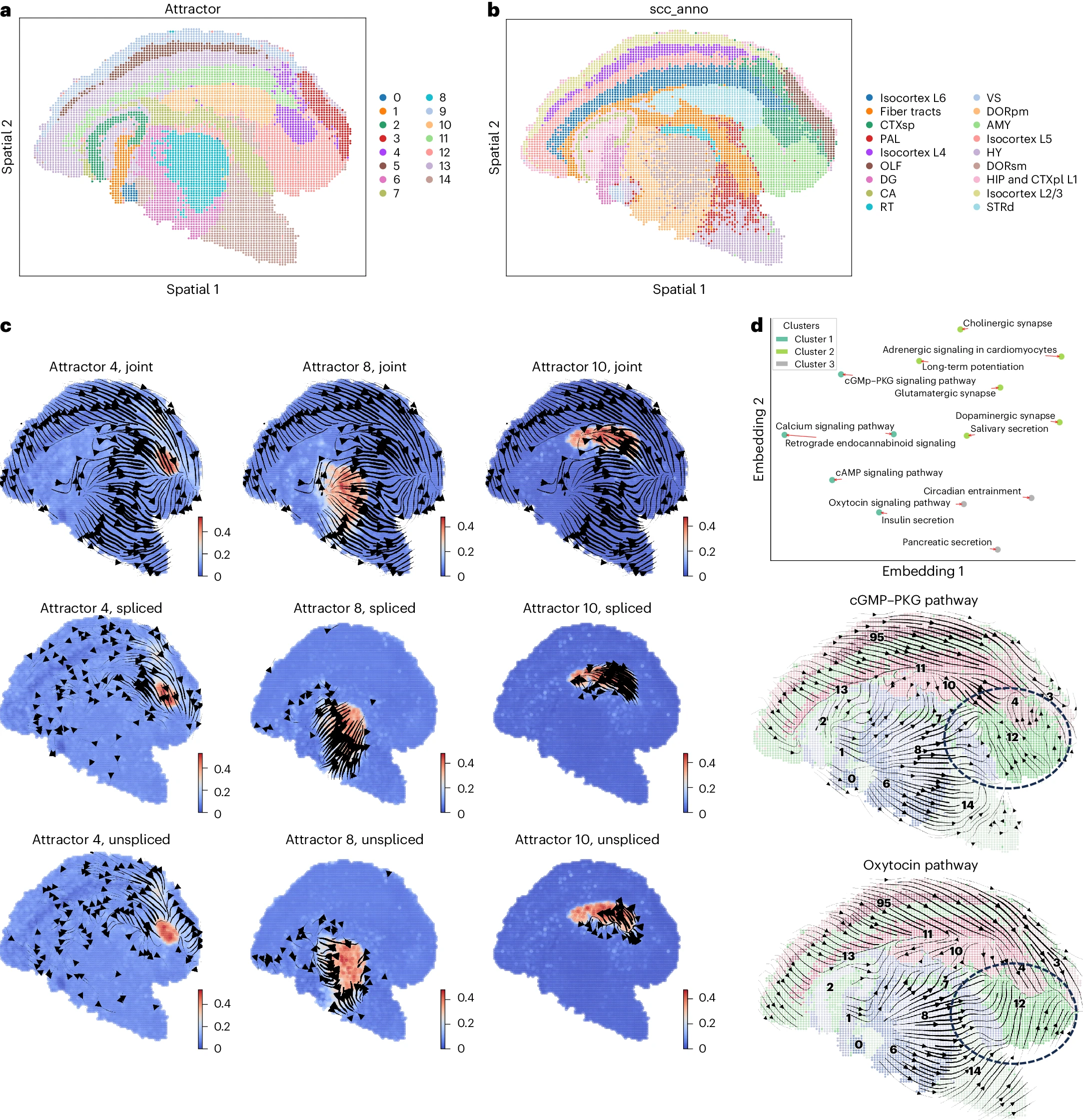
a,b. 细胞的空间位置按 STT 吸引子(a)和原始研究中的注释(b)进行着色。 c. 吸引子 4、8 和 10 中的局部张量流线。 d. 通路动力学的二维嵌入(上)和两个特定通路的平均张量流线(下),细胞按吸引子着色并嵌入空间坐标中。具有至少八个与 STT 多稳态基因重叠的基因的通路显示在二维嵌入中。
讨论¶
量化和建模未剪接和剪接计数之间的相对丰度,使得能够采用有效的机械方法来剖析来自 scRNA-seq 数据集的细胞状态转变。为了连接基因表达、mRNA 剪接和细胞谱系动力学之间的不同时间尺度,并研究这些状态的潜在吸引子,我们开发了 STT 用于:(1) 构建吸引子特异的过渡张量,(2) 分析概率过渡路径和过渡细胞,(3) 推断导致细胞状态多稳态的基因。这是通过在 (1) 过渡张量模型中的参数推断和 (2) 张量诱导的随机动力系统的多尺度分析之间的迭代计算过程完成的。
与 RNA 速度模型相比,STT 在揭示基因表达和剪接动力学的潜在吸引子以及量化它们之间的过渡方面具有独特性。通过假设多稳态性,STT 对初始状态规范或隐藏时间校正具有鲁棒性。细胞归属函数在估计过渡张量时量化了过渡细胞,自然地桥接了下游的多尺度动力学分析。
为了识别过渡细胞和推断过渡路径,STT 利用计算的过渡张量,而不是直接使用 RNA 速度,如 CellRank 或 Dynamo。在下游分析中,发现多稳态过渡张量与吸引子假设更兼容。STT 在张量构建和动力学解剖之间的迭代方案被发现更能确保这种自洽性。然而,由于吸引子假设不考虑振荡动力学,STT 需要改进以捕捉具有强细胞周期效应的数据集的非平衡特征。
基于速度核的细胞随机游走从过渡张量中推导出来,是连接 STT 中张量推断和动力学分解模块的关键,允许在不同尺度上更好地连接动力学。理论分析表明,不同的速度核选择会导致各种形式的常微分方程或随机微分方程的连续极限。在 STT 中,使用内积核构建细胞随机游走,证明其与基因表达的随机化学朗之万模型一致,而余弦核则正确恢复了速度场的方向性,用于可视化吸引子内的局部流线。除了微分方程模型之外,将来可能有趣的是在 RNA 速度的化学主方程框架中制定 STT。
作为一种基于机械模型的方法,STT 在多个方面可能会有所改进。与其在方程 (1) 中使用吸引子特异的非线性基因表达速率函数的零阶近似,不如考虑最近提出的用于基因调控网络推断的高阶基因相互作用。可以将包括单细胞表观基因组学或蛋白质组学数据在内的多模态信息纳入多稳态动力系统,以增强过渡张量计算。在多稳态模型中自动检测根状态和目标状态始终是一个挑战,先前的知识或了解与细胞分化能力相关的属性可能会有所帮助。
总体而言,STT 提供了一种统一的方法,通过跨越不同时间尺度和组织区域的过程,从单细胞数据集中提取时空信息。我们的方法允许对组织时空结构进行多尺度描述,连接基因表达和剪接的微观动力学,以及新兴吸引子之间的细胞状态转变的宏观动力学。
方法¶
基因表达和剪接模型中的多稳态性¶
我们使用一个简单的动力学模型,并在每个稳态附近采用不同的参数来近似基因 \(i\) 的 mRNA 剪接动力学:
这里,\(\alpha_{c, i}\) 是吸引子 \(c\) 中状态依赖的未剪接 mRNA 转录速率,\(\beta_i\) 是 mRNA 剪接速率,\(\gamma_i\) 是 mRNA 降解速率。假设系统接近稳态,我们有 \(\epsilon_i=\alpha_{c, i}-\beta_i U_i, \eta_i=\beta_i U_i-\gamma_i S_i\),其中 \(\epsilon_i\) 和 \(\eta_i\) 是独立且同分布的均值为零的高斯变量。由于表达的不可变性
由于不同基因的参数是独立估计的,为简化符号,这里我们省略了基因下标 \(i\),并引入下标 \(k\) 表示细胞索引。吸引子指示函数 \(1_{k \in \Omega_c}\) 使用用户提供的细胞标签或标准 Leiden 或 Louvain 聚类算法输出进行初始化,并在迭代中使用归属函数进行更新(如下所述)。估计得出的解为:
其中 \(m_c=\frac{\sum_{k=1}^{N_{\mathrm{C}}} U_k 1_{k \in \Omega_c}}{N_c}\)。与标准 RNA 速度模型中的稳态参数估计相比,多稳态模型中的剪接速率参数 \(\beta\) 不仅是吸引子类型特异的,还取决于未剪接和剪接计数。
对于每个细胞 \(k\),其计数为 \(\left(U_k, S_k\right)\),其相对于每个吸引子 \(c\) 的速度定义为 \(v_{k, u, c}=\alpha_c^{(*)}-\beta^{(*)} U_k, v_{k, s, c}=\beta^{(*)} U_k-S_k\),其中下标 \(u\) 和 \(s\) 分别对应未剪接和剪接计数。该估计对于每个基因重复,因此得到一个四维过渡张量 \(v_{k, l, c, g} \in \mathbb{R}^{N_{\mathrm{C}} \times 2 \times K \times N_{\mathrm{G}}}\)。
基于张量和空间约束的过渡动力学 接下来,STT 基于计算的张量、基因表达相似性和空间坐标(如果有)构建个体细胞之间的马尔可夫链过渡概率(图 1g)。过渡概率由三个部分构成:\(P=w_1 P^{\mathrm{v}}+w_2 P^{\mathrm{c}}+\left(1-w_1-w_2\right) P^{\mathrm{s}}\),其中 \(P^{\mathrm{v}}, P^{\mathrm{c}}\) 和 \(P^{\mathrm{s}}\) 分别是由速度、相似性和空间核引导的过渡概率。这里 \(w_1\) 和 \(w_2\) 是算法的超参数,用于平衡张量动力学、基因表达相似性和空间邻近性的不同模态的影响。它们对输出的影响已在补充图 6 中测试。
为了构建 \(P^{\mathrm{v}}\),我们首先通过沿吸引子维度取平均值将吸引子特异张量转换为吸引子无关的速度 \(V\):
这里 \(\rho_{k, c}\) 表示细胞 \(k\) 在吸引子 \(c\) 中的归属函数。位于吸引子盆地固定点附近的稳定细胞 \(j\) 使得 \(\rho_{j, d}=1\),而位于鞍点附近的过渡细胞 \(k\) 在 \(\rho_{k}\) 中有多个正分量,指向细胞可以过渡到的吸引子。
这里 \(\rho_{k, c}\) 表示细胞 \(k\) 在吸引子 \(c\) 中的归属函数。位于吸引子盆地固定点附近的稳定细胞 \(j\) 使得 \(\rho_{j, d}=1\),而位于鞍点附近的过渡细胞 \(k\) 在 \(\rho_{k}\) 中有多个正分量,指向细胞可以过渡到的吸引子。
计算了张量后,我们使用内积核 \({}^{49}\)(补充说明 1)构建由速度引导的过渡概率 \(P^{\mathrm{v}}\)。从细胞 \(k\) 到 \(l\) 的过渡倾向权重为 \(w_{k l}=\exp \left(V_{k, u}^T \Delta U_{k l}+V_{k, s}^T \Delta S_{k l}\right)\),其中 \(\Delta U_{k l}=U_l-U_k\) 和 \(\Delta S_{k l}=S_l-S_k\)。由这种核引导的随机游走与方程(1)的 SDE 模型一致(参考文献 \({}^{49}\) 和补充说明 1)。由细胞相似性引导的过渡概率 \(P^{\mathrm{c}}\) 是从基于基因表达计数的扩散图的高斯核构建的 \({}^{2}\)。最后,空间约束过渡概率 \(P^{\mathrm{s}}\) 是从空间位置坐标的高斯核构建的,使得具有相似空间位置的细胞更有可能在彼此之间进行过渡。因此,这些细胞更有可能被分配到相同的吸引子盆地。
为了计算吸引子中的归属函数,我们使用 GPPCA \({}^{57}\) 算法分解构建的随机游走过渡概率矩阵 \(P\),并对非平衡马尔可夫链进行粗粒化,获得 \(\rho_{k, c}\)。该算法允许对细胞随机游走的非平衡过渡概率矩阵进行因式分解和“粗粒化”,这对于大多数由速度引导的动力学来说是真实的,从而获得数据中的吸引子以及细胞在每个吸引子中的相关位置(即归属)。使用 GPPCA 算法同时获得吸引子层面的粗粒化(cg)过渡概率矩阵 \(P_{\mathrm{cg}}^{K \times K}\)(\(K\) 是吸引子的总数)。给定细胞的归属函数,其过渡熵可以定义为 \(\varepsilon_i=-\sum_{c=1}^K \rho_{i, c} \ln \rho_{i, c}\)。较大的熵值表明细胞在吸引子之间进行过渡的倾向较高。
参数估计和吸引子归属量化的迭代方案¶
在获得归属函数后,更新张量模型的参数以纳入细胞在吸引子中位置的不确定性。我们定义损失函数
其中 \(\lambda\) 表示动力学参数正则化项的强度。直观上,吸引子 \(c\) 中的“稳定细胞”在回归损失函数中具有较大的权重值,因为对稳态的置信水平较高。我们解析地求解优化器
其中 \(m_c=\frac{\sum_{k=1}^{N_{\mathrm{C}}} U_k \rho_{k, c}}{\sum_{k=1}^{N_{\mathrm{C}}} \rho_{k, c}+\lambda}\) 反过来,使用新优化的参数更新的张量会导致更新的归属函数。在 STT 中,我们采用一个迭代方案来联合更新张量参数和吸引子归属,
其中上标 \(n\) 表示迭代次数,DynamicalAnalysis 表示更新归属函数的过程。一旦归属函数在一定阈值内不再改进,或者迭代次数超过允许的最大迭代次数,该方案便停止。
为了准确剖析多稳态动力学,我们在每次迭代中基于基因对模型拟合优度进行基因筛选,包括表现出多稳态性的基因。拟合优度指标或基因多稳态评分定义为 \(1-\frac{J\left(\alpha_c, \beta, \rho_{k, c}\right)}{N_{\mathrm{C}}(\operatorname{Var}(U)+\operatorname{Var}(S))}\),其中 \(N_{\mathrm{C}}\) 表示细胞数量。仅使用多稳态评分超过某个阈值的筛选基因的张量来计算速度核,从而更新归属函数。STT 的超参数及其在分析数据集中选择的值见补充表格 1 和 2。
为了稳健控制迭代方案,我们引入了一个监控模块,该模块输出训练集(默认情况下占所有样本大小的 80%)和测试集(占所有样本的 20%)中基因的多稳态评分。训练集用于拟合动力学参数(\(\left.\alpha_c, \beta\right)\)),并在测试集中计算基因的多稳态评分。监控模块输出多稳态评分和通过阈值的基因数量。根据输出,用户可以交互式地选择(1)修改用于筛选多稳态基因的阈值,(2)调整张量诱导核相对于基因表达相似性或空间核的权重,以提高过渡矩阵的质量,或者(3)决定是否停止迭代,从而促进自适应精度。监控模块的界面示于补充图 1f。我们还在补充表格 3 和补充图 10 中展示了 STT 算法的效率和可扩展性。
初始化迭代¶
为了开始迭代,STT 请求输入现有的聚类结果,通过独热编码创建吸引子归属。推荐使用数据集的先前生物学注释或空间区域分割结果作为输入。当没有此类信息时,用户可以采用聚类算法,如 Leiden 或 Louvain,根据表达计数(仅剪接或剪接和未剪接联合)或细胞的空间位置对细胞进行聚类。STT 对初始化的鲁棒性进行了研究(补充图 Z)。无论何时用户倾向于使用其他聚类方法和/或更系统的分析,STT 都提供了一个选项,可以将用户生成的聚类输出作为 STT 初始化的输入。
动态流形和过渡路径的可视化¶
为了可视化细胞的低维嵌入,STT 使用每个细胞 \(k\) 的联合状态 \(x_k=\left(U_k, S_k\right) \in \mathbb{R}^{2 N_{\mathrm{G}}}\) 作为降维算法如主成分分析(PCA)或统一流形近似与投影(UMAP)的输入。为了可视化动态流形,我们将细胞在二维平面中的位置定义为 \(y_k=\sum_{c=1}^K \rho_{k, c} \mu_c\),其中 \(\mu_c\) 是每个吸引子的 PCA 或 UMAP 嵌入的中心,\(K\) 是吸引子数量。然后,使用期望最大化算法为所有 \(y_k\) 构建高斯混合密度估计 \(\mathcal{P}(y)\),其中 \(K\) 个成分的初始权重是前一节中推导的吸引子层面、粗粒化随机游走过渡概率矩阵 \(P\) 的平稳分布。动态流形的表面计算为 \(\phi(y)=-\ln \mathcal{P}(y)\)。在二维平面中使用线性(PCA)或非线性(UMAP)投影方法与余弦核计算速度 \(V_k=\left(V_{k, u}, V_{k, s}\right) \in \mathbb{R}^{2 N_{\mathrm{G}}}\) 的流线。给定初始和最终状态,使用过渡路径理论 \(\frac{58}{}\) 和 PyEMMA 软件包 \({}^{59}\) 计算过渡路径及其在总过渡概率流中的比例。
数据可用性¶
本文使用的所有数据集均可公开获取。数据集的详细预处理过程在补充说明中描述。合成电路的模拟数据集可在以下网址获取:https://github.com/cliffzhou92/STT/tree/release/data。人类肺 A549 细胞系的 EMT 数据集可在 GSE147405 获取。胰腺数据集(最初在 GSE132188 可用)和成人骨髓数据集(最初在 https://data.humancellatlas.org/explore/projects/091cf39b-01bc-42e5-9437-f419a66c8a45 可用)可以从 scvelo==0.2.4 软件包的内置数据集中下载(https://scvelo.readthedocs.io/en/stable/api.html)。小鼠脑和鸡心的空间数据集以及用于插补的 scRNA-seq 数据集可以从 https://doi.org/10.5281/zenodo.6798658 (ref. 62) 下载。具有未剪接和剪接计数的 Stereo-seq 小鼠脑数据集从 Spateo 软件包下载(https://github.com/aristoteleo/spateo-tutorials, https://www.dropbox.com/s/c5tu4drxda01m0u/mousebrain_bin60.h5ad?dl=0)。KEGG 数据库最初在 Enrichr 网页上可用(https://maayanlab.cloud/Enrichr/#librariesdownloaded),使用 gseapy==1.0.4 下载。用于分析的处理数据集也存储在 https://disk.pku.edu.cn/link/AAD1681DAD531D47699D459BB46C4651D8。
代码可用性¶
STT 作为 Python 包实现,可在以下网址获取:https://github.com/cliffzhou92/STT/tree/release。用于模拟的源代码和重现本文中所有分析的笔记本文件也可在以下网址获取:https://github.com/cliffzhou92/STT/tree/release/example_notebooks。