TFvelo gene regulation inspired RNA velocity estimation

摘要¶

RNA 速度与细胞命运密切相关，是基于单细胞 RNA 测序数据派生出来的优雅物理解释下，预测细胞状态的重要指标。现有的大多数 RNA 速度模型旨在从每个单独基因的未剪接和剪接 mRNA 之间的相位延迟中提取动态。然而，未剪接/剪接 mRNA 的丰度可能不足以提供动态建模的有效信号，导致相位图像拟合不良。受到 RNA 速度可能由转录调控驱动的想法的启发，我们提出了 TFvelo，这是一种扩展 RNA 速度概念到各种单细胞数据集的方法，不依赖剪接信息，通过引入基因调控信息。我们在合成数据和多个单细胞 RNA 测序（scRNA-Seq）数据集上的实验表明，TFvelo 能够准确地拟合相位图像上的基因动态，并有效地从 RNA 丰度数据推断出细胞伪时间和轨迹。TFvelo 为单细胞数据的 RNA 速度建模开辟了一条稳健且准确的新途径。

引言¶

单细胞 RNA 测序（scRNA-seq）为研究个体细胞的基因表达提供了丰富信息。为了将 scRNA-seq 分析的范围从静态快照扩展到捕捉细胞动态，而无需随时间跟踪活细胞，开发了许多轨迹推断方法，如 PAGA、Monocle、Slingshot 和 Palantir。这些方法允许在细胞和基因水平进行假时间分析，但通常需要标注初始细胞。近年来，提出了 RNA 速度理论，该理论用物理信息方法描述了基因丰度的时间导数，通过模拟未剪接（未成熟）和剪接（成熟）mRNA 之间的关系。通过跨多个基因组合速度，可以从细胞间的转换概率推断出基于速度的假时间和细胞命运。为了估算 RNA 速度，引入了假定稳态的标准方法 velocyto。ScVelo 在放弃稳态假设的情况下，采用期望最大化（EM）方法更好地重建了底层动力学。

最近，开发了几种方法来改进 RNA 速度的估计。例如，VeloAE 利用自动编码器和低维空间平滑 RNA 速度。在未剪接/剪接空间中，DeepCycle 使用自动编码器映射与细胞周期相关的基因。UniTVelo 直接设计了一个时间函数来模拟剪接 RNA 水平。与确定性模型相比，VeloVI、Pyrovelocity 和 veloVAE 使用贝叶斯推断框架估算 RNA 速度。LatentVelo 使用变分自动编码器将未剪接和剪接表达嵌入潜在空间，从而获得 RNA 速度的低维表示。CellDancer 用神经网络模型化基因的转录、剪接和降解率。此外，动态也可以通过额外信息进行建模，例如 Dynamo 通过使用新/总标记的 RNA-seq 改进 RNA 速度模型。利用单细胞多组学技术，RNA 速度分析可以扩展到蛋白质丰度（protaccel）和单细胞 ATAC-seq（MultiVelo）数据集。然而，这些额外的组学数据或标记可能在大多数单细胞数据集中成本高昂甚至无法获得。

尽管 RNA 速度理论在许多研究中改进了单细胞轨迹、假时间和基因调控推断，但当前的 RNA 速度模型仍面临严峻挑战。首先，RNA 速度模型总是独立处理每个基因，没有考虑潜在的调控，尽管通过整合基因调控机制分析有望帮助推断细胞命运。其次，这些模型在大多数基因上无法很好地拟合基因动态，可能是因为单细胞分辨率下 mRNA 剪接的转录动态可能不足以提供足够的信号。大多数传统方法假设未剪接和剪接表达之间的联合图应在相位肖像中形成顺时针曲线，因为它们之间存在相位延迟，然而，这种情况很少从数据中观察到。未剪接 mRNA 计数的高稀疏性和噪声性可能是一个重要原因。剪接过程的短时间尺度也可能使

从未剪接和剪接 RNA 之间的延迟中提取动态变得困难。最后，RNA 速度模型只能应用于具有未剪接/剪接或新/总标签的 scRNA-seq 数据集。然而，在某些数据集中，可能无法获得未剪接/剪接数据，例如通过荧光原位杂交（FISH）技术获得的数据，以及由于隐私限制的一些人类测序数据。这些挑战激励我们基于调控而不仅仅是依赖于未剪接/剪接计数来构建基因动态。

在单细胞研究领域，基因调控已被广泛探索。在本研究中，我们旨在基于基因之间的潜在调控推断基因动态和细胞命运。为此，我们研究了基因调控模式与 RNA 速度之间的关系，发现 RNA 速度可以近似估计为转录因子（TFs）表达水平的线性组合。值得注意的是，具有非零权重的 TFs 在功能上与目标基因显著相关。此外，我们发现 TF 及其目标之间的表达联合分布可能在共表达图上形成顺时针曲线，表明它们之间存在相位延迟。这些发现暗示 TF 的丰度也可以用来构建 RNA 速度的动态模型。

在本研究中，我们提出了 TFvelo 来根据 TFs 的表达水平模拟 RNA 速度，其中速度指 RNA 丰度的变化率。TFvelo 的计算框架依赖于广义 EM 算法，该算法迭代更新 TFs 的学习表现、细胞的潜在时间和动态方程中的参数。TFvelo 可以完成以前 RNA 速度研究的分析，如基因特定相位肖像拟合、速度建模、无需标注初始状态即可推断假时间，以及通过基于速度的转换流图可视化细胞命运。与依赖剪接信息的方法不同，TFvelo 可以稳健地工作在未剪接计数稀疏的基因上，甚至在没有剪接信息的数据集上。使用合成数据和多个真实 scRNA-seq 数据集，我们展示了 TFvelo 模型能够捕获 TFs 目标的相位肖像动态，准确推断细胞的伪时间和发展轨迹，并帮助探索生物学发现。

结果¶

发现：RNA 速度可以通过转录因子（TFs）的丰度近似估算

以下两个发现支持了通过转录调控来建模 RNA 速度的观点。我们发现，先前方法的 RNA 速度模型可以近似地作为 TFs 丰度的线性组合来估算。在 scRNA-Seq 胰腺数据集上，针对一个目标基因，我们使用最小绝对收缩和选择算子（LASSO）回归来预测由 scVelo 建模的 RNA 速度，基于 TFs 和目标基因本身的表达水平（图 S1a）。这里，我们使用默认参数在胰腺数据集上运行 scVelo 流程以获取速度，并且仅将 LASSO 回归应用于那些由 scVelo 建模的基因。我们将所有的 TFs 输入到 LASSO 中，得到了一个稀疏的权重向量，其中只有一些 TFs 具有非零权重。因此，基因$ g $ 的 RNA 速度可以估算为：

\[ v_g=\sum_{TF_i \in S_g} w_{g, TF_i} e_{TF_i} + w_{g, g} e_g \]

其中，( $S_g$ ) 表示 TFs 的集合，( $e_{TF_i}$ ) 和 ( $e_g$ ) 分别是 $TF_i$ 和基因 ( $g$ ) 的表达水平，( $w_{g, TF_i}$ ) 和 ( $w_{g, g}$ ) 是 $TF_i$ 和目标基因本身的权重。

细胞被分为训练集和测试集，以评估 LASSO 模型。测试集上的回归结果显示预测速度与标记速度之间的高度相关性，如图 S1b,c 所示，这表明可以根据其转录因子（TFs）的表达来预测目标基因的速度。此外，如表 S1 所示，具有非零权重的转录因子在与目标基因功能链接的转录因子集中显著富集（根据 ENCODE TF- 目标数据库 38），p 值为 6.66e-06（单侧 t 检验），这进一步表明速度可以通过转录因子进行建模。其次，由于转录因子与目标之间的调控关系，它们的表达水平会异步变化，这可能在相位肖像中产生顺时针曲线。正如预期的那样，我们在一些转录因子 - 目标对的共表达图中发现了所需的顺时针曲线（图 S2），这与未剪接 - 剪接空间中现有速度模型的理论预测相似。这些发现表明，有可能基于转录因子的表达构建一个新型的 RNA 速度模型，而不使用未剪接/剪接 RNA 计数或任何额外的实验组学数据和标签。

使用 TFvelo 估计 RNA 速度¶

在这里，我们报道了 TFvelo，用于估计目标基因的 RNA 速度，该估计基于目标基因本身及其潜在的转录因子的丰度。图 1a 提供了一个胰腺数据集中的基因相位肖像拟合的例子，解释了 TFvelo 如何优于基于剪接的方法。以前的方法侧重于建模剪接和未剪接 RNA 之间的动态，而 RNA 剪接的转录动态可能无法提供足够的信号，且二维未剪接 - 剪接 RNA 水平可能过于嘈杂或稀疏，不易拟合。相比之下，TFvelo 考虑了目标基因与多个转录因子之间的关系，通过学习调控的表征，允许基于基因调控网络进行更稳健和准确的建模。

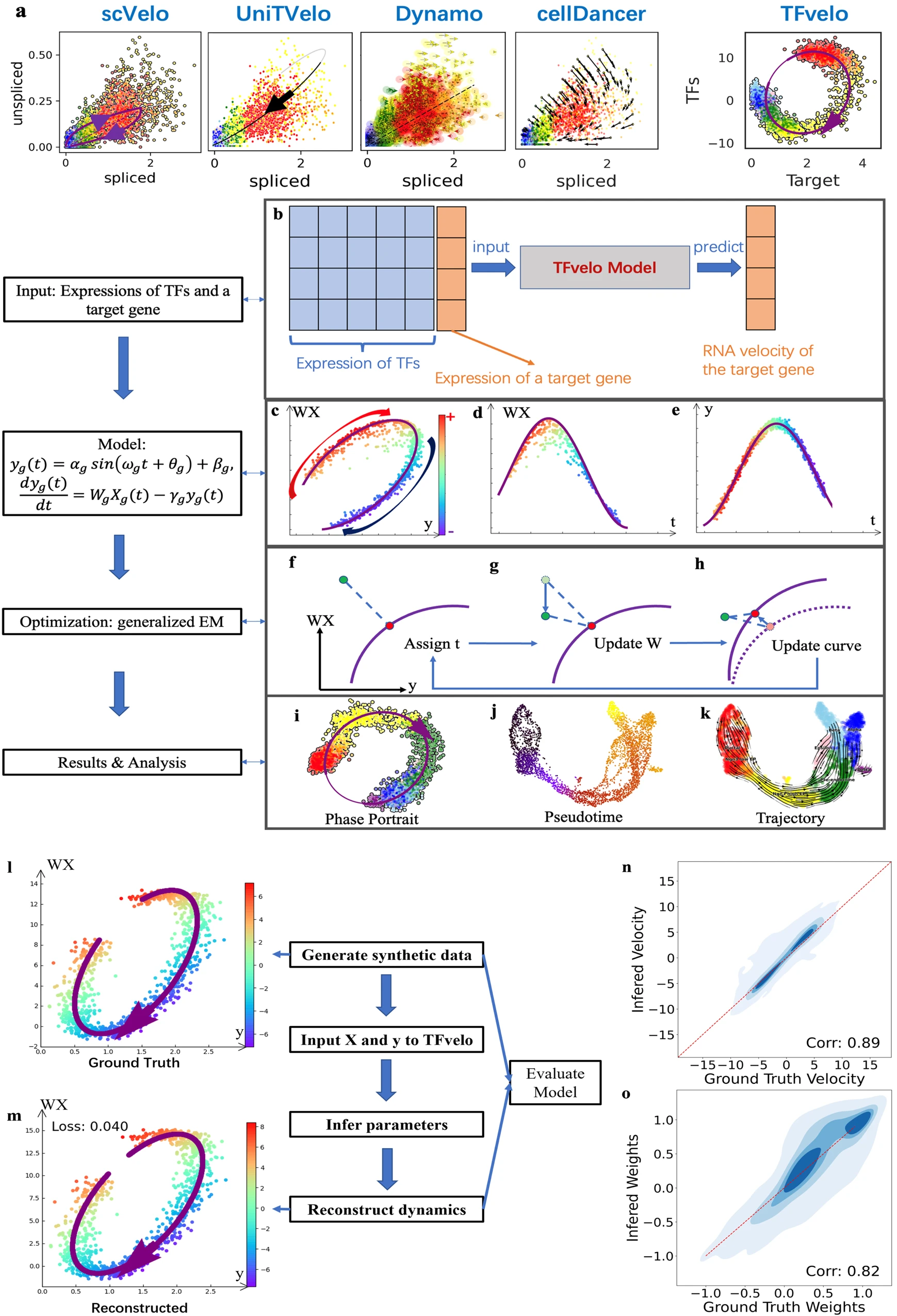
a. 使用 TFvelo 和之前方法对胰腺数据集中 LITAF 基因构建的动态进行比较。细胞的着色方式与图 2a 中的相同。 b. TFvelo 的工作流程。 c-e. 在 $WX-y$ 空间的相位肖像图，关于伪时间的 $WX$ 图，以及关于伪时间的 $y$ 图。这三个面板共享表示 RNA 速度的颜色条。为了简化，$W_g, X_g, y_g$ 和 $t_g$ 分别简写为 $W, X, y$ 和 $t$。 f-h. 广义 EM 算法每次迭代中的步骤。这里紫色线代表模型当前的预测。 f. 为每个细胞分配潜在时间（绿色显示），以找到对应的目标点（红色显示），该点是细胞在紫色线上的最近点。 g. 优化权重 $W$，使所有细胞沿 $WX$ 轴移动，以最小化所有细胞的平均损失。 h. 优化动态函数中的参数，以将曲线上的目标点更接近每个细胞。 i-k. TFvelo 结果的可视化和分析，包括相位肖像拟合、伪时间推断和细胞轨迹预测。 l-o. 在合成数据集上的模拟。 l. 生成的合成动态的一个例子。 m. 使用均方误差损失，对（l）中显示的样本的 TFvelo 重构动态。 n. 地面真实速度和推断速度的联合图，及其斯皮尔曼相关性。红色参考线表明地面真实值等于推断值。 o. 地面真实权重和推断权重的联合图，及其斯皮尔曼相关性。数据来源为源数据文件。

对于目标基因 $g$，TFvelo 探索其表达水平 $y_g$ 与转录因子对 $g$ 的调控之间的关系。在 TFvelo 中，RNA 速度 $\frac{d y_g(t)}{d t}$，定义为 RNA 丰度的时间导数，由涉及的转录因子的丰度 $\mathbf{X}_g$ 和基因本身决定，

\[ \frac{d y_g(t)}{d t}=h\left(\mathbf{X}_g(t) ; \Psi_g\right) \]

采用自上而下的策略，该策略可以将基因动态放松到更灵活的表达轮廓 $\underline{\underline{13}}$，TFvelo 直接设计了目标基因表达水平的轮廓函数，

\[ y_g(t)=f\left(t ; \Phi_g\right) \]

其中 $\Psi_g$ 和 $\Phi_g$ 是两组基因特异性的时间不变参数，分别描述转录因子对目标基因的影响和相图的形状。考虑到以前的研究 $34,39,40,41$ 中使用线性模型来表示基因调控，$h\left(\mathbf{X}_g(t), y_g(t) ; \Psi_g\right)$ 被实现为一个线性模型 $\frac{d y_g(t)}{d t}=\mathbf{W}_{\boldsymbol{g}} \mathbf{X}_{\boldsymbol{g}}(t)-\gamma_g y_g(t)$。$y_g(t)$ 的轮廓函数可以灵活地从一系列二阶可微函数 $\frac{13}{}$ 中选择，这是作为函数实现的（见方法部分）。这是因为正弦函数可以模拟从上调和下调开始的非单调动态（例如，图 S8 中的基因 MGST3），这对于依赖单一切换时间点的方法是不可行的 ${ }^9, 10,18$。

为了优化，将所有可学习参数分为三组，分别是特定于细胞的潜在时间 $t$、转录因子的权重 $\mathbf{W}_{\boldsymbol{g}}$ 和相图的形状参数 $\psi_g$，其中 $n_{\text{cell}}$ 和 $n_{TF}$ 分别代表细胞数量和基因数量。采用泛化的 $\mathrm{EM}^{\underline{42}, 43}$ 算法在每次迭代中通过交替更新这三组参数来最小化损失函数（见图 $\underline{\text{If}-\mathrm{h}}$）。基于对所有基因的优化模型，我们可以得到一个转换矩阵，并计算伪时间和速度流以进行细胞轨迹分析。详细信息请参阅方法部分。

TFvelo 可以重建动态模型并在合成数据集上检测调控关系。¶

为验证 TFvelo 能从数据中检测到潜在的动态，我们首先在一个合成数据集上测试它（见方法部分），其中一个目标基因由 10 个转录因子调控，相应的权重为正或负，分别代表该转录因子可能上调或下调目标基因。我们在 1000 个细胞上随机生成 200 个合成基因动态，每个都有不同的基础真实参数。对于每一个，TFvelo 重建动态函数并根据转录因子和目标的模拟表达估计每个转录因子的权重。

TFvelo 的性能通过斯皮尔曼相关系数来评估，该系数是基础真值和重建值之间的相关系数。在 20 次优化迭代后，转录因子权重的基础真值与推断权重之间的斯皮尔曼相关系数为 0.823，速度估计的相关系数为 0.894（见图 1n，o）。高度的一致性显示 TFvelo 可以有效地重建潜在动态。此外，高 F1 分数（0.944）和高接收者操作特性（ROC）曲线下面积比（0.962）也证明 TFvelo 能正确识别权重是正是负。此外，我们在这里使用普通 EM 方法作为基线，通过移除转录因子权重的优化步骤以及多点初始化策略。经过 20 次优化迭代后，这个基线的表现远不如 TFvelo（见图 S 4）。有关合成数据集的详细信息，请参阅补充信息第 3 节。

为了在真实的单细胞 RNA 测序（scRNA-seq）数据上评估 TFvelo，我们首先将其应用于 E15.5 小鼠胰腺的数据集 9，该数据集在以前的 RNA 速度研究中被广泛采用。TFvelo 预测的伪时间和轨迹可以识别分化过程（见图 2a, b）。与以前的方法相比，TFvelo 在相图拟合上显示出优势。示例基因显示在图 2c, S7 中。图 2c 比较了不同方法的相图拟合，而图 S7 提供了通过 scVelo 和 TFvelo 得到的基于基因特异性潜在时间的基因表达动态。TFvelo 发现，H19 基因在早期发展中起重要作用 44，在 Ngn3 高表达阶段开始时增加然后减少。对于 MAML3，只有 TFvelo 能正确检测从上调开始然后转为下调的过程。其他方法无法正确检测前内分泌细胞（绿色）与包括 α、β、δ 和 ε 细胞（蓝色、浅蓝色、紫色和粉色）的那些内分泌细胞群之间的顺序。

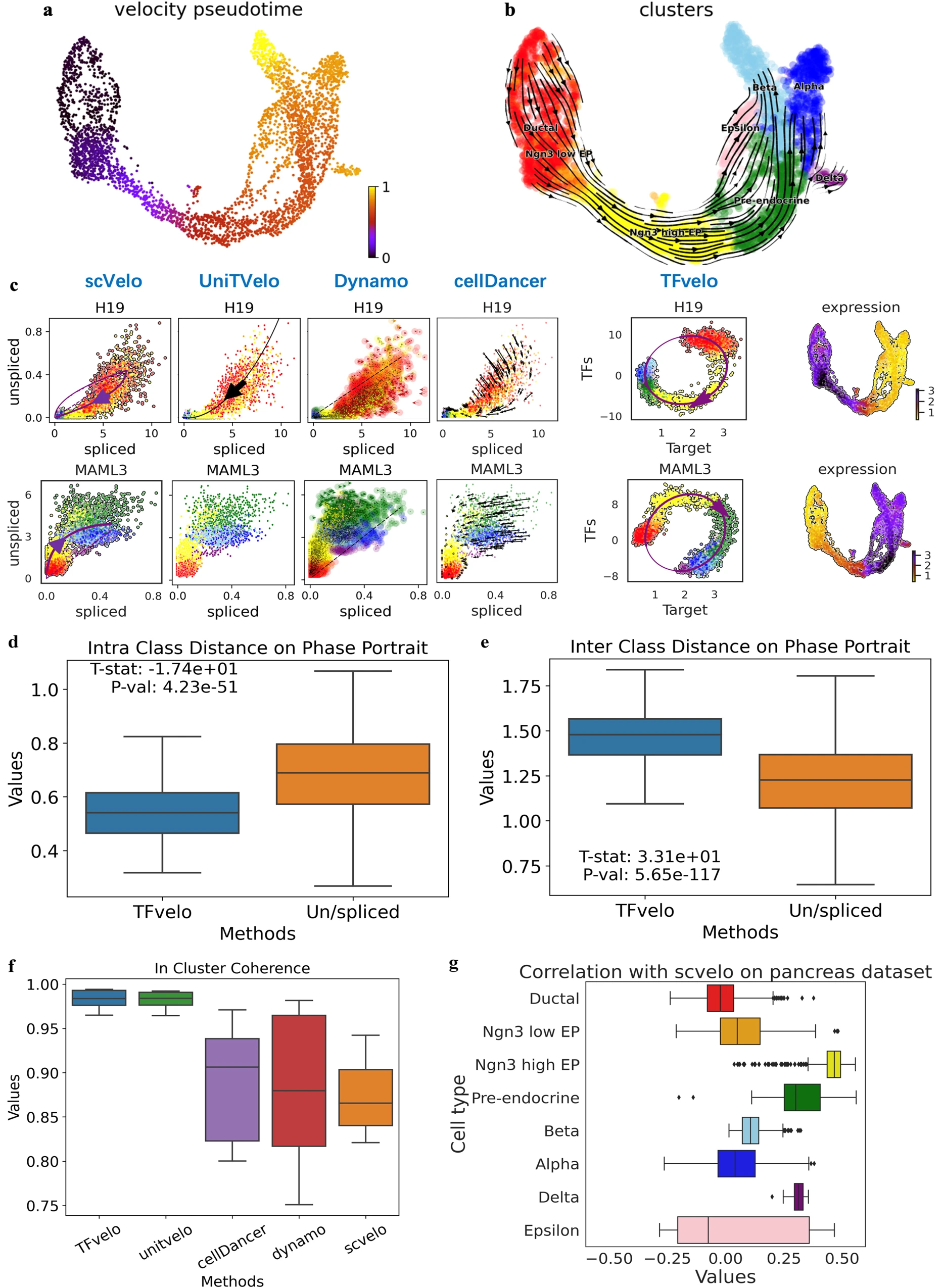
a. 通过 TFvelo 推断的 UMAP 基础嵌入空间中的伪时间。
b. 投影到 UMAP 的流线图。Ngn3 低/高 EP 代表神经元生成素 3 低/高表达的上皮细胞。
c. 两个示例基因用于说明相图中的动态拟合。细胞的颜色与图 (b) 中的相同。
d. 相图中类内距离的比较。应用双侧 t 检验，不进行调整。
e. 相图中类间距离的比较。应用双侧 t 检验，不进行调整。
f. 群集间一致性的比较。
g. 通过 scVelo 和 TFvelo 获得的速度向量之间的余弦相似性。
对于图 (d, e, f, h) 中的箱线图，下、中、上铰链分别对应于第一四分位数、中位数和第三四分位数。晶须延伸到从铰链到分布的 1.5 倍四分位距之外。图 d、e、f 中箱线图的样本数为 405。图 g 中每个箱线图（从上到下）的样本数分别为 916、262、642、592、591、481、70 和 142。

为了定量评估相图的拟合效果，我们提出了三个指标：（1）相图上的类内距离，反映同一类型的细胞在相图上的聚集程度（越低越好）。（2）相图上的类间距离，反映不同类型的细胞在相图上的分离程度（越高越好）。（3）相图上的拟合误差，衡量每个细胞到构建模型的归一化距离。这些指标是基于所有方法都能共同建模的基因来计算的。对于“类内距离”和“类间距离”，我们对 TFvelo 的相图和所有基线方法（包括 scVelo、Dynamo、UniTVelo 和 cellDancer）共享的未剪接/剪接相图，在同一基因上获得的值进行配对样本 T 检验。TFvelo 的结果（图 2d, e）显示出极高的显著性优势（p = 4.23e-51 和 p = 5.65e-117）。与基于未剪接/剪接的方法相比，TFvelo 实现了更低的类内距离、更高的类间距离和更低的拟合误差（图 S5h）。总之，TFvelo 可以通过使用学习到的具有转录调控功能的特征，解决由噪声未剪接/剪接数据造成的 RNA 速度建模问题。

为了定量评估学到的流动性，我们采用了 VeloAE11 和 UniTVelo13 中采用的两个指标：“跨边界方向正确性（CBDir）”和“群集内一致性（ICCoh）”。CBDir 利用具有真实注释的边界细胞评估从一种细胞类型过渡到下一种细胞类型的正确性。ICCoh 通过计算同一群集内细胞间的余弦相似性来衡量群集内高维空间中的速度平滑度。如图 2f, S5i 所示，TFvelo 的中位数与 UniTVelo 相似，且显著优于其他方法。此外，TFvelo 甚至实现了高速度一致性（图 S5j），这表明 UMAP 空间中相邻细胞的 RNA 速度更一致。TFvelo 和 UniTVelo 实现更高一致性评分的直接原因是它们可以在相邻细胞中生成更平滑的速度流（图 S5b, d）。这可能归因于 TFvelo 和 UniTVelo 模型的相似性。这两种方法都直接以时间为高阶可微函数模型基因丰度，而不假设可能打断模型平滑度的切换点。此外，为了显示 TFvelo 和 scVelo 推断的速度之间的相关性，我们计算了两种方法得到的速度向量的余弦相似性，使用的是共同建模的基因。每种细胞类型的余弦相似性分布显示在图 2g 中。

然后我们根据最佳拟合基因进行 KEGG 通路富集分析，并观察到与胰岛素分泌和胰高血糖素信号通路（图 3a）有强烈的关联富集。此外，我们发现 REST 和 HMGN3 在建模大多数目标基因时持续表现出高绝对权重（图 3b）。在检查 UMAP 分布时，可以清楚地看到 REST 表达在分化过程中减少，而 HMGN3 表达增加（图 3c）。以前

的研究已经确定 REST 是胰腺器官发生期间内分泌分化的关键负调节器 45,46。早期研究还报告 HMGN3 是胰腺细胞胰岛素分泌的调节器 46。我们进一步分析了这两个转录因子在胰岛素分泌途径中建模基因的权重。REST 始终具有负权重，而 HMGN3 始终表现出正权重（图 3d），这与之前的发现一致。

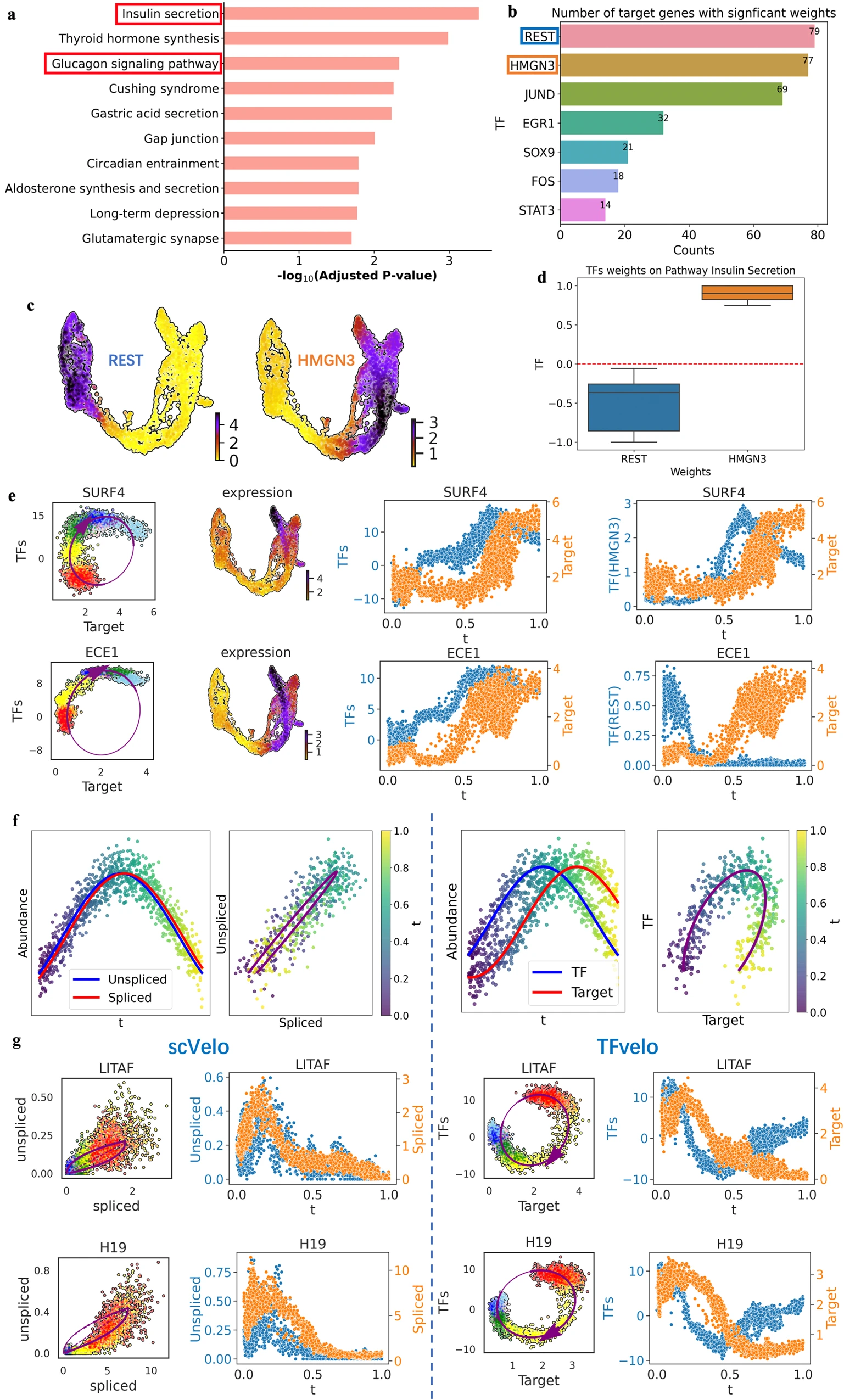
a. 基于胰腺数据集中由 TFvelo 最佳拟合的基因进行的 KEGG 通路富集分析。调整后的 p 值是使用 Fisher 精确测试计算的。 b. 在多个目标基因上具有高权重的转录因子（TF）列表。计数表示转录因子在目标基因中具有的归一化权重的绝对值大于 0.5 的基因数量。 c. 在 UMAP 上 REST 和 HMGN3 的分布。 d. 在胰岛素分泌途径中的基因上模型中转录因子 REST 和 HMGN3 的权重分布。下、中、上铰链分别对应于第一四分位数、中位数和第三四分位数。晶须延伸到从铰链到分布的 1.5 倍四分位距之外。REST 和 HMGN3 的箱线图样本数分别为 7 和 5。 e. 两个示例基因的相位分析。每行从左到右：相位图拟合，UMAP 上的丰度分布，学习到的转录因子表示（WX）和伪时间下的目标基因，以及伪时间下的转录因子和目标基因的丰度。 f. 在模拟中，两个变量的可视化，其中它们之间的时间延迟非常短或相对较长。颜色条反映伪时间。 g. 在两个示例基因上，scVelo 和 TFvelo 获得的相位图拟合和伪时间下的表达水平的比较。

对转录因子（TF）和目标基因之间的相位延迟的比较显示在图 $\underline{\text{3e}}$ 中，图中清楚地显示了学习到的转录因子表示（$\mathbf{WX}$）和目标基因表达之间的明显相位延迟。我们还分析了转录因子和单个目标之间的相位延迟。在两个基因中，HMGN3 在模型化 SURF 时具有正权重，可以观察到它们之间的相位延迟。相反，REST 在模型化 ECE1 时具有负权重，它们的变化显示出负相关性。

除了未剪接数据中的稀疏性和噪声（图 S6）外，剪接动态的时间尺度也可能使从未剪接和剪接 RNA 之间的延迟中提取动态变得困难。据报道，剪接可以在 $30 \mathrm{s}$ 内完成 $\frac{47}{}$，这个持续时间远短于 scRNA-seq 数据集中描述的整个分化过程的时间尺度。因此，未剪接和剪接 mRNA 之间的相位延迟可能太短，无法在相位图中捕获。这可能是理论曲线无法在未剪接 - 剪接相位图中观察到的一个原因（图 $3 \mathrm{f}, \mathrm{g}$）。图 $3 \mathrm{f}$ 提供了模拟，以说明即使在相同水平的噪声下，变量之间较短的相位延迟也可能使拟合相位图更具挑战性。我们还观察到来自 scRNA-seq 数据集的现象支持我们的假设。图 $3 \mathrm{g}$ 显示，在某些基因上，剪接和未剪接几乎同步变化，而 TFvelo 可以检测到更清晰的相位延迟以进行动态建模。

TFvelo 可以模拟胚胎原始红细胞数据集上的细胞分化过程¶

胚胎原始红细胞数据集选自小鼠胚胎的转录谱 $\underline{48}$，并已在 RNA 速度研究 $\underline{\underline{13}}$ 中采用。使用 TFvelo，通过流线可视化的伪时间和细胞发展流与红细胞系的发展一致，从血细胞祖细胞到红细胞（图 $\underline{\text{aa}}$b）。相比之下，一些先前的方法无法捕获这种发展动态，如图 $4 \mathrm{~d}$ 所示。

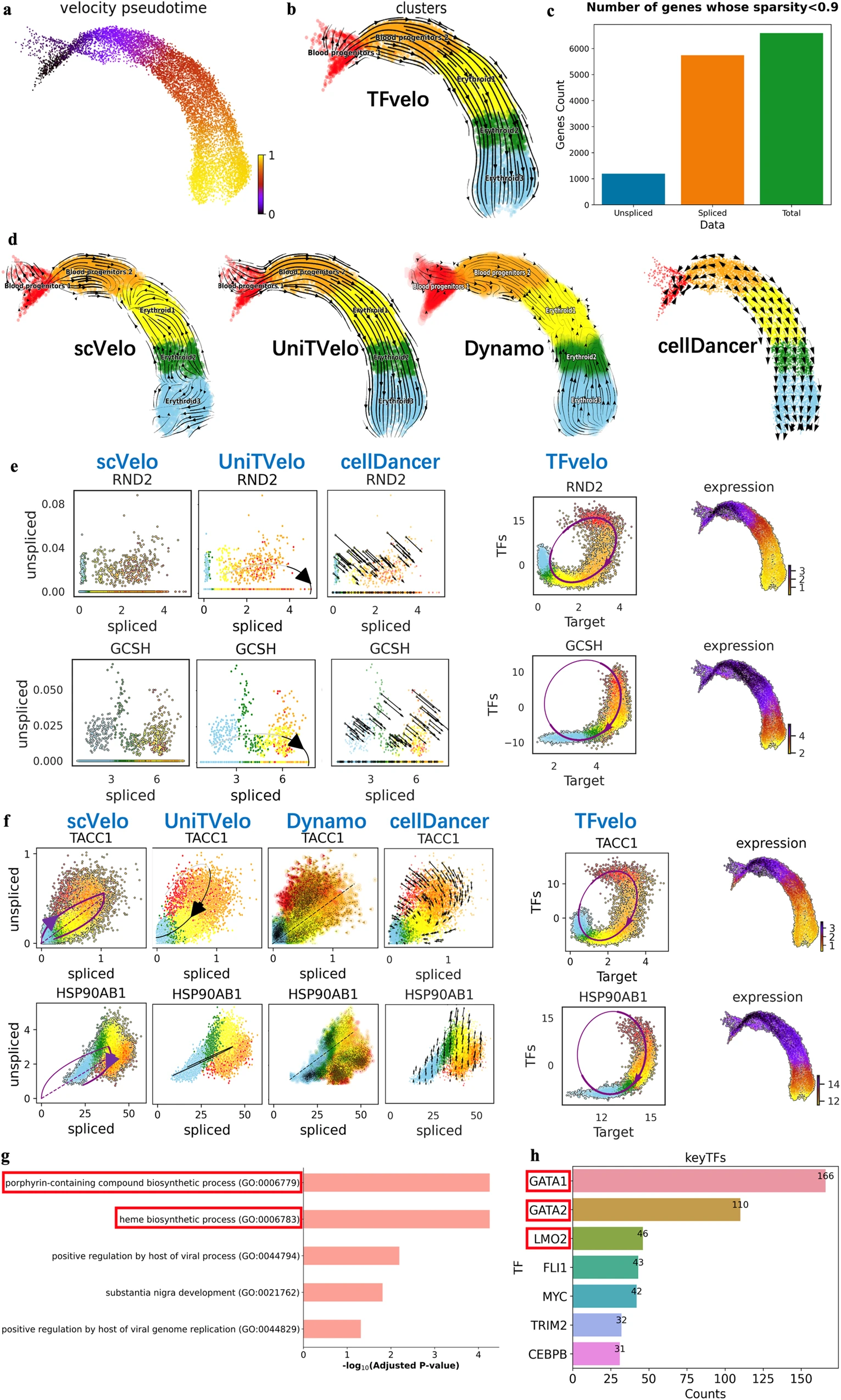
a. 通过 TFvelo 推断的伪时间映射到基于 UMAP 的嵌入中。 b. 由 TFvelo 获得的流线图。 c. 未剪接、剪接和总 mRNA 计数的稀疏性。基因的稀疏性定义为： d. 由基线方法获得的流线图。每个图根据方法的教程绘制。 e. 在具有稀疏未剪接计数的基因上的相位图拟合。 f. 在具有稀疏未剪接计数的 TACC1 和 HSP90AB1 上的相位图拟合。 g. 基于最佳拟合基因的 GO 术语生物过程富集。调整后的 p 值使用 Fisher 精确测试计算。 h. 每个转录因子的目标基因数量，其中权重的绝对值大于 0.5。

数据的稀疏性是单细胞 RNA 测序 (scRNA-seq) 研究的一个常见挑战。考虑到只有大约 20% 的读取包含未剪接的内含子序列 9，未剪接的稀疏丰度对于相位图中的动态拟合是一个重大障碍。我们对未剪接、剪接和总 mRNA 计数的稀疏性进行了定量分析，结果显示在图 4c 中，验证了未剪接计数的高稀疏性。图 4e 展示了两个具有非常稀疏未剪接计数的基因的比较，以说明 TFvelo 在解决稀疏问题上的优势。尽管这些基因可以通过预处理期间的筛选和选择，但它们仍然太稀疏，无法为基于剪接的模型提供足够的信息进行良好拟合。图 4f 提供了更多的示例基因，比较了 TFvelo 和基线方法。TACC1 被注释为在形成分化组织之前促进细胞分裂的基因 49。在我们的实验中，TACC1 的表达最初增加，在血细胞祖细胞 2 中达到最高值，这正是在分化为红细胞之前。随后，TACC1 的表达随着从红细胞 1 到红细胞 3 的伪时间逐渐减少。相比之下，以前的方法未能检测到从血细胞祖细胞 1（红色）开始的动态。至于 HSP90AB1，只有 TFvelo 能够从学习到的相位图中捕捉到正确的动态。

接下来，我们基于最佳拟合的基因进行 GO 术语富集分析，发现最显著的 GO 术语包括含卟啉化合物生物合成过程（GO:0006779）和血红素生物合成过程（GO:0006783），这些直接与红细胞发育相关（图 4g）。此外，在大多数目标基因上具有高权重的转录因子是 GATA1、GATA2 和 LMO2（图 4h），所有这些转录因子都被报道参与红细胞分化。GATA1 在调控红细胞成熟和功能的转录方面发挥重要作用 50。GATA2 被验证为调控造血干细胞的增殖和分化 51。LMO2 是一个桥接分子，组装红细胞的 DNA 结合复合体 52。这些发现展示了 TFvelo 在从单细胞数据中检测重要调控基因的潜力。

TFvelo 可以仅使用 scRNA-seq 数据达到与 Multivelo 相当的性能¶

接下来，我们将 TFvelo 应用于一个包含多组学数据的 10x 胚胎小鼠大脑数据集，该数据集同时提供了转座酶可及染色质测序（ATAC-Seq）53 和 scRNA-seq。这个数据集曾在 Multivelo 研究中使用，Multivelo 是一个为多组学数据集设计的 RNA 速度模型，能够捕捉染色质可及性和未剪接 mRNA 之间的动态 12。在这个数据集中，如 Multivelo 研究所描述，外侧脑室下区的径向胶质（RG）细胞可以产生神经元、星形胶质细胞和少突胶质细胞。皮层层的发展遵循从内到外的模式，年轻细胞上升到上层，而较老的细胞则保持在更深的层次。RG 细胞可以分裂，产生作为神经干细胞的中间祖细胞（IPC），这些细胞最终在皮层层生成各种成熟的兴奋性神经元。

TFvelo 推断的伪时间与 Multivelo 的结果非常相似（图 5a, b），并且两种方法都能正确识别大多数细胞的分化方向。值得注意的是，TFvelo 达到这种性能时没有使用 ATAC-seq 数据。图 5c 展示了两种方法的相位图拟合，其中 Multivelo 能够展示一个额外的 c-u 相位图，反映了 ATAC-seq 和未剪接 mRNA 之间的联合图。

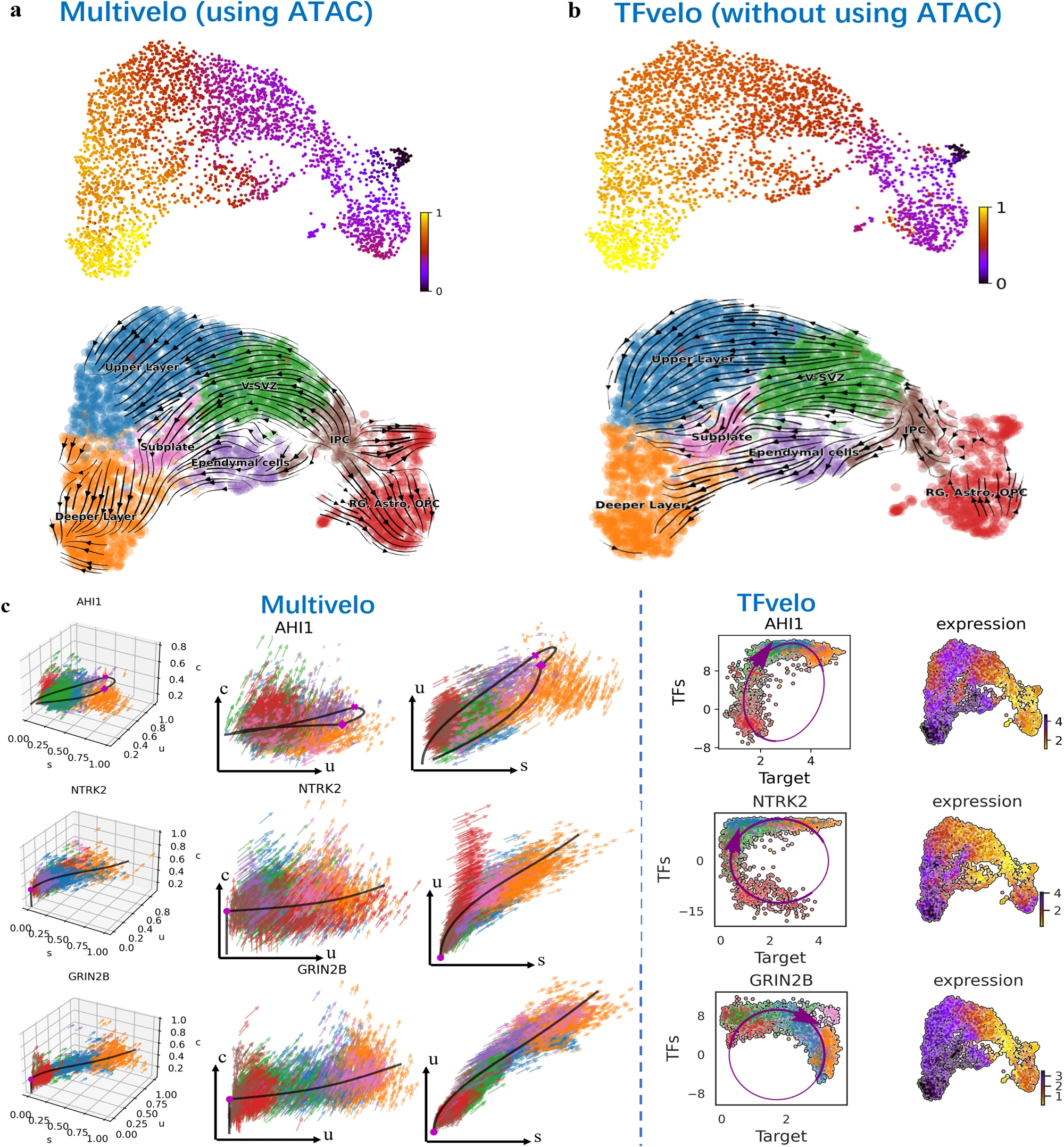
a. 由 Multivelo 推断的伪时间和轨迹投影到基于 UMAP 的嵌入中。 b. 由 TFvelo 推断的伪时间和轨迹投影到基于 UMAP 的嵌入中。 c. 在三个示例基因（分别为 AHI1、NTRK2 和 GRIN2B）上比较 Multivelo 和 TFvelo。对于 Multivelo 的图，(c) 表示 ATAC-seq 中的染色质可访问性。

关于 AHI1 基因，Multivelo 错误地构建了一个循环动态，相反，TFvelo 正确地捕捉到了动态，表现为从 V-SVZ 细胞（绿色）开始表达量一致增加。对于 NTRK2 基因，TFvelo 正确捕捉到这种动态，而 Multivelo 错过了开始时的减少过程。在 GRIN2B 基因上，TFvelo 和 Multivelo 都检测到了相同的动态，表达量从开始到终止阶段持续增加。这些结果表明，通过提取多个转录因子的特征，TFvelo 可以在不使用 ATAC-seq 的情况下，比 Multivelo 更好地拟合单个基因的动态。

尽管 ATAC-seq 可以为 RNA 动态建模提供额外信息，但由于多种问题，这可能是具有挑战性的。例如，高稀疏且近乎二进制的 ATAC-seq 数据 54 可能导致不同类型的细胞混合，这对相位图拟合构成挑战。如图 5c 的第一列所示，即使 ATAC/未剪接/剪接的 3D 相位图也不能提供足够的信息进行动态建模。具体来说，c 轴（ATAC）无法帮助区分不同类型的细胞（图 5c 的第二列）。此外，通过 ATAC 获得的峰值更难直接与特定基因关联。相比之下，TFvelo 可以直接将多个转录因子链接到目标基因的建模中。结果显示，TFvelo 能够在转录因子 - 目标相位图（图 5c 的第四列）中很好地提取与分化过程一致的动态。

TFvelo 可以在没有剪接信息的数据集上预测细胞命运¶

接下来，TFvelo 被应用于另一个由 88 个人类植入前胚胎在胚胎第 3 天到 755 天收集的 1,529 个细胞组成的单细胞 RNA 测序数据集。由于在线数据集服务器没有提供原始测序文件（参见数据可用性声明），那些依赖于剪接/未剪接信息的 RNA 速度方法不可行。相比之下，TFvelo 仍然成功识别了细胞的伪时间和发展轨迹，如图 6a、b 所示。此外，动态模型成功地拟合了目标基因的表达模式，如图 6d 所示为示例。具体来说，对 PPP1R14A 的动态预测在转录因子 - 目标图上揭示了一个顺时针曲线，并发现在受精后第 5 天表达水平增加和减少之间的变化点。与 TFvelo 的结果一致，已报道 PPP1R14A 的表达在斑马鱼早期胚胎的发展初期开始增加然后在整个发展过程中下降，表现出高动态 56。TFvelo 发现 RGS2 的表达在开始时最高，并随伪时间减少，这可以得到早期发现的支持，即 RGS2 在早期胚胎发展中起关键作用 57。

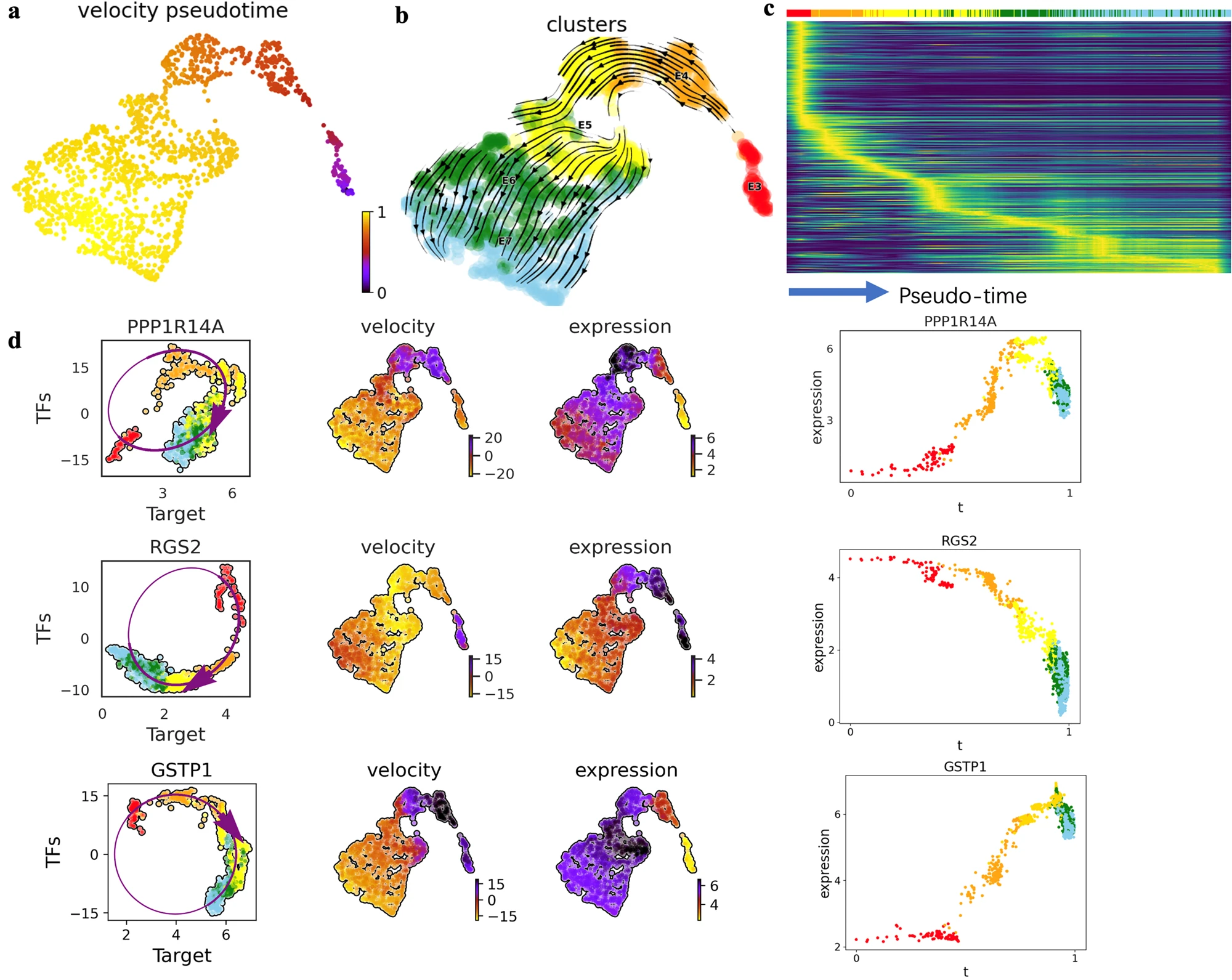
a. 由 TFvelo 推断的伪时间映射到基于 UMAP 的嵌入中。 b. UMAP 的流线图。 c. 显示沿伪时间解析的前 300 个可能性排名基因的表达动态的热图。 d. 分别在三个具有高可能性的示例基因（PPP1R14A、RGS2 和 GSTP1）上构建的动态模型。在每一行中，从左到右的三个子图分别展示相位图拟合、在 UMAP 上的速度分布、在 UMAP 上的表达分布，以及沿伪时间解析的表达动态。

讨论¶

最近在 RNA 速度方法的发展为单细胞数据的时间分析提供了新的见解。然而，现有方法常常无法在未剪接/剪接空间中很好地拟合细胞动态，部分原因是信号不足以及高度的稀疏性和噪声。受到转录因子（TFs）与目标之间的相位延迟也可提供时间信息的启发，我们提出了 TFvelo 来基于 TFs 的丰度估计基因动态。与需要数据中剪接信息的先前方法不同，TFvelo 模型使用 TFs 和目标基因本身的表达水平来建模目标基因的动态。在计算框架中，采用了广义 EM 算法，使得潜在时间、TFs 的权重和动态函数中的可学习参数可以在每次迭代中交替更新。

在合成数据集上的实验验证了 TFvelo 能够从数据中检测到潜在的动态。在各种 scRNA-seq 数据集和一个 10× 多组学数据集上的结果进一步证明了 TFvelo 可以很好地拟合基因动态，在 TFs 表示和目标之间的相位图上显示出期望的顺时针曲线。此外，TFvelo 可用于推断伪时间、细胞轨迹，并检测在分化中起重要作用的关键 TFs。此外，与依赖剪接信息的先前 RNA 速度模型相比，TFvelo 在这些 scRNA-seq 数据集上可以实现更好的性能，并且可以灵活地应用于没有剪接信息的更多类别的数据集。

由于需要学习 TFs 的表示，TFvelo 的时间效率低于相同框架中的基线方法，例如 scVelo。这在应用于大规模数据集时可能是一个弱点。通过并行使用更多的 CPU 执行 TFvelo 可以减少运行时间。同时，TFvelo 仍然无法很好地拟合某些基因的动态（见图 S14）。改进更多基因的建模仍然是一个需要进一步探索的挑战性任务。未来，可能探索更复杂的模型来替代 TFvelo 中用于估计每个 TFs 权重的当前线性模型。用于描述表达动态的正弦函数也可以灵活地被其他功能形式替换。此外，最近提出的用于改进基于未剪接/剪接的 RNA 速度模型的想法也可以在 TFvelo 的进一步开发中采用，包括带贝叶斯推理的随机建模 14、多组学整合 22 和宇宙时间推断 13。

方法¶

数据预处理¶

我们使用 scVelo10 中的默认设置进行数据准备过程，不同之处在于 TFvelo 应用于总 mRNA 计数，即未剪接和剪接计数的总和。此外，在筛选掉少于 2% 的细胞中可以检测到的基因后，我们选择前 2000 个高变异基因（HVGs），并通过每个细胞的总计数对这些 HVGs 的表达谱进行标准化。默认情况下，基于欧几里得距离在主成分分析空间（默认为 30 个主成分）中计算最近邻图（默认为 30 个邻居）。之后，根据最近邻计算每个细胞的一阶和二阶矩（均值和未中心化方差）。这些步骤与 scv.pp.filter_and_normalize() 和 scv.pp.moments() 的实现方式相同。

此外，为了找到选定的 2000 个高变异基因中潜在的转录关系，我们参考了 ENCODE TF-target 数据集 38 和 ChEA TF-target 数据集 58 中注释的 TF- 目标配对。如果这两个数据集中至少一个标记了 TF- 目标配对的调控关系，那么在建模目标基因的动态时，该 TF 将被包括在涉及的 TFs 集合中。

计算框架 of TFvelo¶

针对基因 $g$，TFvelo 假设 RNA 速度 $\frac{d y_g(t)}{d t}$ 由涉及的转录因子的表达水平 $\mathbf{X}_g$ 和目标基因本身 $y_g$ 决定，即：

\[ \frac{d y_g(t)}{d t}=h\left(\mathbf{X}_{\boldsymbol{g}}(t), y_g(t) ; \Psi_g\right) \]

使用自上而下的策略 $\underline{\underline{13}}$，TFvelo 直接设计了目标基因表达水平的轮廓函数，以使基因动态更加灵活，表达式为：

\[ y_g(t)=f\left(t ; \Phi_g\right) \]

$\Psi_g$ 和 $\Phi_g$ 是两组基因特异的、时间不变的参数，分别控制转录因子对目标基因的影响和目标基因相图的形状。我们的发现和早期研究 $\frac{39}{}$ 已经显示，根据基于表达数据的线性回归模型中学习到的参数推断调控关系是可行的。此外，线性模型具有很高的可解释性，很少出现过拟合现象。因此，为了展示基于基因调控关系建模 RNA 速度的能力，我们简单地采用了线性模型作为 $h\left(\mathbf{X}_g(t), y_g(t) ; \Psi_g\right)$，该模型可以将多个转录因子的表达水平 $\mathbf{X}_{\boldsymbol{g}} \in R^{n_{T F}}$ 从 $n_{T F}$ 维空间映射到 1 维表示 $\mathbf{W}_g \mathbf{X}_g$，其中 $\mathbf{W}_{\boldsymbol{g}}$ 是权重向量，$n_{T F}$ 代表涉及的转录因子数量。因此，转录因子和目标基因 $g$ 之间的动态方程可以写成：

\[ \frac{d y_g(t)}{d t}=h\left(\mathbf{X}_g(t), y_g(t) ; \Psi_g\right)=\mathbf{W}_g \mathbf{X}_g(t)-\gamma_g y_g(t) \]

其中 $t \in[0,1)$ 是分配给每个细胞的潜在时间，$\gamma_g$ 是降解率。

此外，$y_g(t)$ 的轮廓函数可以从那些二阶可微函数 $\frac{13}{}$ 中灵活选择。为了简化，我们的实现中使用了正弦函数设计 $y_g(t)$，这是高阶可微的，适合捕捉相图上的曲线。此外，与那些假设基因表达应遵循先增后减模式（或此整个过程的一部分）的模型不同，TFvelo 更加灵活，也可以用正弦函数模型化基因动态，其中表达最初减少然后增加：

\[ y_g(t)=f\left(t ; \Phi_g\right)=\alpha_g \sin \left(\omega_g t+\theta_g\right)+\beta_g, \]

在计算框架中，$\alpha_g, \beta_g, \theta_g$ 是需要学习的基因特异性参数。$\omega_g$ 固定为 $2 \pi$，以使得 $y_g(t)$ 在 $t \in[0,1)$ 内是单峰的，这遵循了大多数当前方法的共同假设。通过使用正弦函数，TFvelo 能够在不定义增长期和减少期之间的切换时间点的情况下，模拟每个基因的动态 $9,10,14,18$。为了优化 TFvelo 中的参数，采用了广义 $\mathrm{EM}^{42,43}$ 算法，以下将进行讨论。

广义 EM 算法的优化¶

为了简化数学表达，这里我们将 $\mathbf{W}_{\boldsymbol{g}}, \mathbf{X}_{\boldsymbol{g}}, y_g, \alpha_g, \beta_g, \theta_g, \gamma_g$ 和 $\omega_g$ 分别记为 $\mathbf{W}, \mathbf{X}, y, \alpha, \beta, \theta, \gamma$ 和 $\omega$。因此，方程 $(\underline{5}, \underline{4})$ 可以写成

\[ y(t)=\alpha \sin (2 \pi t+\theta)+\beta, \]

\[ \frac{d y(t)}{d t}=\mathbf{W} \mathbf{X}(t)-\gamma y(t) . \]

从动态模型方程 (6, ㄱ) 中，我们可以推导出，

\[ \mathbf{W X}(t)=\alpha \sqrt{4 \pi^2+\gamma^2} \sin (2 \pi t+\theta+\phi)+\beta \gamma, \phi=\arctan \left(\frac{2 \pi}{\gamma}\right) \]

对于模型化一个基因，假设观察 $\mathbf{X}_{\mathbf{c}}^{\text {obs }}$ 和 $y_c^{o b s}$ 是细胞 $c$ 中转录因子和目标基因的归一化表达水平，$s_c^{o b s}$ 是细胞 $c$ 的状态空间表示，$\hat{s}\left(t_c\right)$ 是时间 $t_c$ 时的模型状态，我们有 $s_c^{o b s}=\left[\mathbf{W X}_{\mathbf{c}}^{\text {obs }}, y_c^{o b s}\right]$ 和 $\hat{s}\left(t_c\right)=\left[\mathbf{W X}\left(t_c\right), y\left(t_c\right)\right]$。为了找到最适合所有细胞观察结果的相位轨迹 $\hat{s}(t)$，我们定义损失函数为：

\[ L=\sum_c\left\|s_c^{o b s}-\hat{s}\left(t_c\right)\right\|^2=\sum_c\left(\mathbf{W} \mathbf{X}_{\mathbf{c}}^{\text {obs }}-\mathbf{W X}\left(t_c\right)\right)^2+\left(y_c^{o b s}-y\left(t_c\right)\right)^2, \]

观察的残差定义为 $e_c=\operatorname{sign}\left(y_c^{o b s}-y\left(t_c\right)\right)\left\|s_c^{o b s}-\hat{s}\left(t_c\right)\right\|^2$，假设它们遵循正态分布 $e_c \sim N\left(0, \sigma^2\right)$，其中基因特异性的 $\sigma$ 在细胞中是常数，观察是独立同分布的。然后我们可以得到似然函数，

$$ \mathcal{L}(\mathbf{W}, \alpha, \beta, \theta, \gamma)=\frac{1}{\sqrt{2 \pi} \sigma} * \exp \left(-\frac{1}{2 \sigma^2} \sum_c\left|s_c^{o b s}(\mathbf{W})-\hat{s}_{

t_c}(\mathbf{W}, \alpha, \beta, \theta, \gamma)\right|^2(1)\right)_b $$

其中 $\hat{s}_{t_c}(\mathbf{W}, \alpha, \beta, \theta, \gamma)$ 代表 $\hat{s}\left(t_c ; \mathbf{W}, \alpha, \beta, \theta, \gamma\right)$。最后，优化算法旨在最小化负对数似然函数：

\[ l(\mathbf{W}, \alpha, \beta, \theta, \gamma)=-\log \left(\frac{1}{\sqrt{2 \pi} \sigma}\right)+\frac{1}{2 \sigma^2} \sum_c\left\|s_c^{o b s}(\mathbf{W})-\hat{s}_{t_c}(\mathbf{W}, \alpha, \beta, \theta, \gamma)\right\|_{(1,1)}^2 \]

在标准 EM 算法中，E 步计算给定观察数据和当前估计参数的似然函数的期望值以更新潜在变量，M 步包括通过优化参数来最大化 E 步中计算的期望。在某些情况下，M 步存在难以处理的问题，可以通过广义 EM 算法解决。条件期望最大化是广义 EM 算法的一种形式，它在每个 M 步中进行多个约束优化 ${ }^{42}$。具体来说，参数可以分成更多的子集，M 步也包括多个步骤，每个步骤优化一组参数，其他参数保持固定 $\frac{43}{}$。

在 TFvelo 中，所有可学习参数可以分为三组，分别是特定于细胞的潜在时间 $t \in R^{n_{\text{cell}}}$，每个转录因子的权重 $\mathbf{W} \in R^{n_{TF}}$ 以及标量 $[\alpha, \beta, \theta, \gamma]$，其中 $n_{\text{cell}}$ 和 $n_{TF}$ 分别代表细胞的数量和涉及的转录因子的数量。采用广义 EM 算法，以便在每次迭代中交替更新这三组参数，以最小化损失函数：

为每个细胞分配 $t$ 在 $[0,1]$ 范围内通过网格搜索。对于每个细胞，在相位图上，由动态模型描述的曲线上的最近点被定义为目标点。步骤 (b) 和 (c) 旨在最小化细胞及其相应目标点之间的平均距离。
通过线性回归更新 $W$，在这些权重上设置界限以最小化损失函数。采用信任域反射算法 ${ }^{\underline{59}}$，这是一种内点类方法，用于解决带不等式约束的线性最小二乘问题。在我们的实现中，默认情况下权重界限设置在 $(-20,20)$ 之间。
通过限制 $\alpha \in(0, \infty), \theta \in(-\pi, \pi)$ 和 $\gamma \in(0, \infty)$ 更新 $[\alpha, \beta, \theta, \gamma]$，以最小化损失函数。

通过迭代执行这三个步骤，可以优化 TFvelo 中每个目标基因的参数。此外，通过结合所有目标基因学到的动态，可以进行多种下游分析。

广义 EM 算法的初始化¶

由于 EM 算法可能会陷入局部最小值，因此参数的初始化按以下步骤进行。首先，过滤掉目标基因表达为 0 的细胞。然后对 $\mathbf{X}, y$ 进行归一化，$\mathbf{X}=\frac{\mathbf{X}}{\operatorname{var}(\mathbf{X})}, y=y / \operatorname{var}(y)$，其中 $\operatorname{var}(\cdot)$ 表示标准差函数。权重 $\mathbf{W}$ 的初始化值为每对 TF- 目标的斯皮尔曼相关系数。对于参数 $\alpha, \beta$ 和 $\gamma$，根据稳态假设 $\left.\dot{y}\right|_{y=\max (\mathrm{y})}=0$，$\gamma$ 可以通过 $\gamma=\left.\frac{\mathbf{W X}}{y}\right|_{y \rightarrow y_{\max }}$ 初始化。在 $y$ 的最大值和最小值点，我们有 $y_{\max }=\alpha+\beta$ 和 $\mathrm{y}_{\min }=-\alpha+\beta$。因此，$\alpha$ 和 $\beta$ 可以通过 $\alpha=\frac{y_{\max }-y_{\min }}{2}$ 和 $\beta=\frac{\mathrm{y}_{\max }+\mathrm{y}_{\min }}{2}$ 分别初始化。这些假设仅用于初始化，在后续的优化过程中，所有参数将被迭代更新。超参数 $\omega$ 设为 $2 \pi$，参数 $\theta$ 初始值设置为不同的值，以使广义 EM 算法从不同的起点开始运行。之后，最终选择损失最小的模型。

伪时间的推断¶

在为每个基因构建动态模型后，TFvelo 将根据所有基因的 RNA 速度组合为每个细胞推断一个基因无关的伪时间。为此，我们首先计算速度与潜在细胞状态转换的余弦相似度以获得转换矩阵。然后分别作为速度推断的转换矩阵及其转置的静止状态，获取终点和根细胞。在推断出根细胞在嵌入空间的位置后，可以计算速度伪时间，这衡量了从根细胞开始走到达一个细胞所需的平均步数。计算伪时间的策略与 scVelo $\underline{10}$ 中的类似。不同之处在于，scVelo 中的转换矩阵是基于剪接 mRNA 的丰度和速度获得的，而在 TFvelo 中则是基于总 mRNA 的丰度和速度。详细信息请参阅第 6 部分补充信息中的“根细胞和终点细胞检测”。

在二维嵌入空间中的速度流¶

为了展示细胞转换，我们默认使用 UMAP 可视化在二维空间中创建流图。为此，我们选择那些损失较低且基因特定时间与伪时间对齐的基因来构建速度流。

对于单细胞数据集，我们首先选择建模误差在底部 50% 的基因。由于正弦函数表现出周期性，我们需要确定细胞的顺序，而不是直接使用潜在时间。我们通过分析潜在时间的直方图来实现这一点。如果在潜在时间的细胞分布中存在几个连续的空白区间，我们将下一个非空白区间的最小值设置为初始状态（标准化潜在时间=0）。相反地，将最后一个非空白区间的最大值设置为最终状态（标准化潜在时间=1）。所有其他细胞的标准化潜在时间将映射在 0 到 1 的范围内。随后，我们选择那些标准化潜在时间与伪时间基于斯皮尔曼相关系数对齐的基因。

评估相位图拟合的指标¶

我们提出三个用于评估相位图拟合的指标：

相位图上的类内距离：这个指标测量相位图上同一类型内的细胞之间的归一化距离。这反映了同类型的细胞在相位图上是否聚集在一起，越低越好。在基于未剪接/剪接的方法中，类内距离定义为：

$$ \text{Dist} = \sum_k \sum_{j \in \text{type}_k} \left[\left(\frac{u_j-u_c^{k}{\operatorname{std}(u)}\right)}2 + \left(\frac{s_j-s_c^{k}{\operatorname{std}(s)}\right)}2\right] $$

其中 $(u_c^k, s_c^k)$ 表示细胞类型 $k$ 的中心，$\operatorname{std}(\cdot)$ 表示标准差，$j$ 表示细胞的索引。对于 TFvelo，距离可以通过将 $u$ 替换为 $W X$ 和 $s$ 替换为 $y$ 来定义。

相位图上的类间距离：这个指标测量相位图上不同细胞类型的分布中心之间的归一化距离，定义为：

\[ \text{Dist} = \sum\_{k_1 \neq k_2} \left[\left(\frac{u_c^{k_1}-u_c^{k_2}}{\operatorname{std}(u)}\right)^2 + \left(\frac{s_c^{k_1}-s_c^{k_2}}{\operatorname{std}(s)}\right)^2\right] \]

这反映了不同类型的细胞在相位图上是否被良好地分离，越高越好。

相位图上的拟合误差：这个指标测量每个细胞与构建的模型在相位图上的归一化距离。这反映了拟合的准确性，计算方式如下。在每个选定基因的相位图上，计算每个细胞与推断模型曲线之间的距离的归一化均方误差。对于 TFvelo 数据，误差为：

\[ \text{Err} = \sum*{j=1}^N \left[\left(\frac{\mathbf{W X}*{\mathbf{j}} - \mathbf{W X}\left(t_j\right)}{\operatorname{std}(\mathbf{W X})}\right)^2 + \left(\frac{y_j - y\left(t_j\right)}{\operatorname{std}(y)}\right)^2\right] \]

其中 $j$ 表示细胞的索引，$t_j$ 表示为细胞 $j$ 建模的潜在时间，$N$ 是细胞总数。$\mathbf{W X}_j$ 和 $y_j$ 指的是细胞在相位图上的位置。$\mathbf{W X}\left(t_j\right)$ 和 $y\left(t_j\right)$ 指的是 TFvelo 给出的模型。类似地，基于未剪接/剪接数据的方法的误差定义为：

\[ \text{Err} = \sum\_{j=1}^N \left[\left(\frac{u_j-u\left(t_j\right)}{\operatorname{std}(u)}\right)^2 + \left(\frac{s_j-s\left(t_j\right)}{\operatorname{std}(s)}\right)^2\right] \]

数据可用性¶

本研究的关键发现支持的所有相关数据均可在文章及其补充信息文件中找到。胰腺内分泌发生数据集 36 包括 27,998 个基因的 3,696 个胰腺上皮和 Ngn3-Venus 融合细胞的单细胞 RNA 测序（10X）数据，这些细胞样本来自小鼠胚胎第 15.5 天。数据可以通过 scvelo.datasets.pancreas() 获取。胚胎原始红细胞数据集选自小鼠胚胎的转录谱 48，提供 9,815 个细胞的 53,801 个基因的表达数据。此数据集由 scvelo.datasets.gastrulation_erythroid() 包含。10x 胚胎小鼠大脑数据集可以在 10x 网站上访问：https://www.10xgenomics.com/resources/datasets/fresh-embryonic-e-18-mouse-brain-5-k-1-standard-1-0-0。为了确保TFvelo与Multivelo之间的公平比较，TFvelo使用与Multivelo相同的RNA数据文件（https://multivelo.readthedocs.io/en/latest/MultiVelo_Fig2.html），该文件包含3,365个细胞和936个基因。本研究中使用的预处理数据提供在：https://github.com/xiaoyeye/TFvelo/blob/main/data/10x_mouse_brain/adata_rna.h5ad。人类植入前胚胎数据集55是一个包括1,529个细胞的单细胞RNA测序数据集，这些细胞来自于从胚胎第3天到第7天的88个人类植入前胚胎。数据通过访问编号E-MTAB-3929从EMBL-EBI下载。在此数据集中，只提供了RNA丰度。因此，那些依赖于剪接/未剪接的RNA速度方法无法使用。ENCODE TF-target 数据库 38 可在以下地址获取：https://maayanlab.cloud/Harmonizome/dataset/ENCODE+Transcription+Factor+Targets。我们还提供了可以直接在TFvelo中使用的预处理文件：https://github.com/xiaoyeye/TFvelo/blob/main/ENCODE.zip。ChEA TF-target 数据库 58 可在以下地址获取：https://maayanlab.cloud/Harmonizome/dataset/CHEA+Transcription+Factor+Targets。我们也提供了可以直接在TFvelo中使用的预处理文件：https://github.com/xiaoyeye/TFvelo/tree/main/ChEA。源数据随本文提供。

代码可用性¶

TFvelo 是在 Python 中实现的，基于 scVelo 包 10。源代码可以从 GitHub 仓库下载：https://github.com/xiaoyeye/TFvelo60。