Vision Mamba Efficient Visual Representation Learning with Bidirectional State Space Model

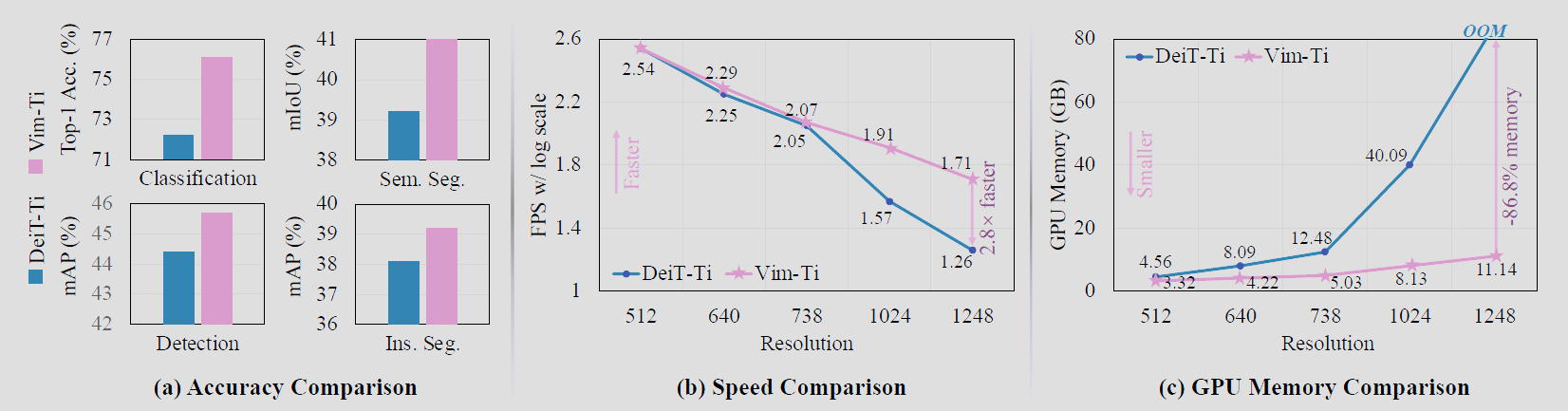
图 1.DeiT[59] 和我们的 Vim 模型之间的性能和效率对比。对于精度比较,我们首先在 IN1K 分类数据集 [9] 上预训练 DeiT 和 Vim,然后我们在不同的下游密集预测任务上微调通用 backbone,即语义分割、目标检测、实例分割。结果表明,所提出的 Vim 在预训练和微调任务上都优于 DeiT。在处理高分辨率图像时,Vim 的计算和内存效率也优于 DeiT。例如,当对分辨率为 1248×1248 的图像 (每张图像 6084 个 tokens) 执行批量推理以提取特征时,Vim 比 DeiT 快 2.8 倍,节省 86.8% 的 GPU 内存。

摘要

最近,具有高效硬件感知设计的状态空间模型 (SSM),即 Mamba 深度学习模型,展现了在长序列建模方面的巨大潜力。同时,纯粹基于 SSM 构建高效通用视觉主干网络是一个很有吸引力的方向。然而,由于视觉数据的位置敏感性和视觉理解对全局上下文的要求,用 SSM 表示视觉数据是一个挑战。在本文中,我们证明了在视觉表示学习中对自注意力的依赖并非必要,并提出了一种新的通用视觉主干网络,它使用双向 Mamba 块 (Vim),利用位置嵌入对图像序列进行标记,并采用双向状态空间模型压缩视觉表示。在 ImageNet 分类、COCO 目标检测和 ADE20k 语义分割任务上,Vim 相比受到广泛关注的视觉转换器 DeiT,取得了更高的性能,同时也展现了显著提升的计算和内存效率。例如,当对分辨率为 1248×1248 的图像执行批量推理以提取特征时,Vim 比 DeiT 快 2.8 倍,节省了 86.8% 的 GPU 内存。结果表明,Vim 能够克服高分辨率图像的计算和内存限制,有望成为下一代视觉基础模型的主干网络。

1. 引言

最新的研究进展导致了人们对状态空间模型 (SSM) 浓厚的兴趣。起源于经典的卡尔曼滤波模型 [29],现代 SSM 擅长捕获长期依赖关系,并且受益于并行训练。一些基于 SSM 的方法,如线性状态空间层 (LSSL)[21]、结构化状态空间序列模型 (S4)[20]、对角状态空间 (DSS)[23] 和 S4D[22],被提出用于处理各种任务和模态下的序列数据,特别擅长于对长期依赖关系的建模。由于卷积计算和近似线性的计算复杂度,它们在处理长序列时效率很高。2-D SSM [2]、SGConvNeXt[36] 和 ConvSSM [51] 将 SSM 与 CNN 或 Transformer 架构相结合以处理二维数据。最近的工作 Mamba[19] 在 SSM 中引入了时变参数,并提出了一种硬件感知算法来实现高效的训练和推理。Mamba 出色的扩展性能表明,它是 Transformer 在语言建模中的一个有前景的替代方案。然而,基于纯 SSM 的通用主干网络用于处理视觉数据 (如图像和视频) 尚未被探索。

视觉转换器 (ViT) 在视觉表示学习方面取得了巨大成功,在大规模自监督预训练和下游任务的高性能上都表现出色。与卷积神经网络相比,其核心优势在于 ViT 可以通过自注意力为每个图像块提供依赖于数据/块的全局上下文。这与使用相同参数 (即卷积滤波器) 对所有位置进行卷积的网络不同。另一个优势是通过将图像视为一系列图像块而无需 2D 归纳偏差来进行模态不可知建模,这使其成为多模态应用的首选架构 [3,35,39]。

同时,用于处理视觉长期依赖关系 (例如处理高分辨率图像) 时,Transformer 中的自注意力机制在速度和内存使用方面带来了挑战。

受 Mamba 在语言建模中取得成功的启发,我们也可以将这种成功从语言领域转移到视觉领域,即设计一种通用高效的视觉主干网络,采用先进的 SSM 方法。然而,Mamba 存在单向建模和缺乏位置感知的两个挑战。为了解决这些挑战,我们提出了 Vim(Vision Mamba) 模型,它结合了双向 SSM 用于数据相关的全局视觉上下文建模,以及位置嵌入用于位置感知的视觉识别。我们首先将输入图像分割为图像块,并将它们线性投影为 Vim 中的向量。图像块在 Vim 块中被视为序列数据,利用所提出的双向选择性状态空间高效压缩视觉表示。此外,Vim 块中的位置嵌入提供了对空间信息的感知能力,使 Vim 在密集预测任务中更加稳健。在当前阶段,我们在 ImageNet 数据集上使用监督图像分类任务来训练 Vim 模型,然后将预训练的 Vim 用作主干网络,以执行下游密集预测任务 (如语义分割、目标检测和实例分割) 的序列视觉表示学习。与 Transformer 一样,Vim 也可以在大规模无监督视觉数据上进行预训练,以获得更好的视觉表示能力。得益于 Mamba 更好的效率,Vim 的大规模预训练可以以更低的计算成本实现。

与其他用于视觉任务的基于 SSM 的模型相比,Vim 是一种纯 SSM 方法,并以序列方式对图像进行建模,这对通用高效的主干网络更有前景。得益于带位置感知的双向压缩建模,Vim 是第一个能处理密集预测任务的纯 SSM 模型。与最有说服力的基于 Transformer 的模型 DeiT[59] 相比,Vim 在 ImageNet 分类任务上取得了更高的性能。此外,对于高分辨率图像,Vim 在 GPU 内存和推理时间方面也更加高效。内存和速度方面的高效性使 Vim 能够直接进行高分辨率视觉理解任务的序列视觉表示学习,而无需依赖 2D 先验 (如 ViTDet[37] 中的 2D 局部窗口),同时比 DeiT 达到更高的精度。

我们的主要贡献可以总结如下:

• 我们提出了 Vim(Vision Mamba),它结合了双向 SSM 用于数据相关的全局视觉上下文建模,以及位置嵌入用于位置感知的视觉理解。

• 无需注意力机制,所提出的 Vim 与 ViT 具有相同的建模能力,但仅需要次二次计算和线性内存复杂度。具体而言,当对分辨率为 1248×1248 的图像执行批量推理以提取特征时,Vim 比 DeiT 快 2.8 倍,并节省了 86.8% 的 GPU 内存。

• 我们在 ImageNet 分类任务和下游密集预测任务上进行了大量实验。结果表明,与受到广泛关注且高度优化的普通视觉 Transformer DeiT 相比,Vim 取得了更高的性能。

2. 相关工作

通用视觉主干网络的架构。在早期,ConvNet[33] 作为计算机视觉的事实标准网络设计。许多卷积神经网络架构 [24,25,32,49,50,55-57,62,71] 被提出作为各种视觉应用的主干网络。具有开创性意义的 Vision Transformer(ViT)[13] 改变了这一格局。它将图像视为一系列平铺的 2D 图像块,并直接应用纯 Transformer 架构。ViT 在图像分类任务上令人惊讶的结果及其扩展能力,促进了大量后续工作 [15,58,60,61]。一条研究路线侧重于引入 2D 卷积先验,设计混合架构 [8,12,14,68]。PVT[65] 提出了金字塔结构 Transformer。Swin Transformer[41] 在移位窗口内应用自注意力。另一条研究路线着眼于通过更先进的设置改进传统 2D 卷积网络 [40,66]。ConvNeXt[42] 回顾了设计空间,并提出了纯卷积网络,其可扩展性能可与 ViT 及其变体媲美。RepLKNet[11] 提出扩大现有卷积网络的核大小以带来改进。

尽管这些主导的后续工作通过引入 2D 先验在 ImageNet[9] 和各种下游任务 [38,73] 上展现出了卓越的性能和更好的效率,但随着大规模视觉预训练 [1,5,16] 和多模态应用 [3,28,34,35,39,48] 的兴起,普通的 Transformer 风格模型重新回到了计算机视觉的中心舞台。更大的建模能力、统一的多模态表示、对自监督学习的友好性等优势,使其成为首选架构。然而,由于 Transformer 的二次复杂度,视觉 token 的数量受到限制。

有大量工作 [6,7,10,31,47,54,64] 试图解决这一长期存在的突出挑战,但很少专注于视觉应用。最近,LongViT[67] 通过扩张注意力机制,构建了一种高效的 Transformer 架构,用于计算病理学应用。LongViT 的线性计算复杂度允许它编码极长的视觉序列。在这项工作中,我们从 Mamba[19] 获得启发,探索构建一种基于纯 SSM 的模型作为通用视觉主干网络,而不使用注意力机制,同时保留 ViT 的序列化、模态不可知建模的优点。

用于长序列建模的状态空间模型。[20] 提出了一种结构化状态空间序列 (S4) 模型,这是一种新颖的替代 CNN 或 Transformer 的方法,用于建模长程依赖关系。S4 在序列长度上的线性缩放属性吸引了进一步的探索。[52] 通过在 S4 层中引入 MIMO SSM 和高效并行扫描,提出了新的 S5 层。[17] 设计了一种新的 SSM 层 H3,几乎填补了 SSM 和 Transformer 注意力在语言建模中的性能差距。[45] 在 S4 的基础上构建了门控状态空间层,通过引入更多门控单元来提高表达能力。

最近,[19] 提出了一种数据相关的 SSM 层,并构建了一种通用语言模型主干网络 Mamba,在大规模实际数据上的各种规模上都优于 Transformer,并且在序列长度上具有线性缩放能力。在这项工作中,我们探索将 Mamba 的成功转移到视觉领域,即构建一种纯基于 SSM 的通用视觉主干网络,而不使用注意力机制。

用于视觉应用的状态空间模型。[26] 使用 1D S4 来处理视频分类中的长程时间依赖关系。[46] 进一步将 1D S4 扩展到处理多维数据,包括 2D 图像和 3D 视频。[27] 结合了 S4 和自注意力的优势,构建了 TranS4mer 模型,在电影场景检测任务上取得了最先进的性能。[63] 在 S4 中引入了一种新颖的选择性机制,在内存占用较低的情况下,大大提高了 S4 在长视频理解任务上的性能。[72] 用更可扩展的基于 SSM 的主干网络取代注意力机制,以在可承受的计算量下生成高分辨率图像和处理细粒度表示。[44] 提出了 U-Mamba,一种混合 CNN-SSM 架构,以处理生物医学图像分割中的长程依赖关系。

上述工作要么将 SSM 应用于特定的视觉应用,要么通过将 SSM 与卷积或注意力机制结合来构建混合架构。不同于它们,我们构建了一种纯基于 SSM 的模型,可以作为通用视觉主干网络。

3. 方法

Vision Mamba (Vim) 的目标是将先进的状态空间模型 (SSM),即 Mamba[19],引入计算机视觉领域。本节首先描述 SSM 的基础知识,然后概述 Vim。接下来详细说明 Vim 块如何处理输入 token 序列,并阐述 Vim 的架构细节。最后,本节分析了所提出的 Vim 的效率。

3.1. 基础知识

基于 SSM 的模型,即结构化状态空间序列模型 (S4) 和 Mamba,灵感来自于连续系统,该系统通过隐藏状态 \(h(t) \in \mathbb{R}^{\mathbb{N}}\) 将 1 维函数或序列 \(x(t) \in \mathbb{R} \mapsto y(t) \in \mathbb{R}\)。该系统使用 \(A \in \mathbb{R}^{N \times N}\) 作为演化参数,使用 \(\mathrm{B} \in \mathbb{R}^{\mathbb{N} \times 1}, \mathrm{C} \in \mathbb{R}^{1 \times \mathbb{N}}\) 作为投影参数。

\[ \begin{aligned} h^{\prime}(t) &=\mathbf{A} h(t)+\mathbf{B} x(t), \\ y(t) &=\mathbf{C} h(t) . \end{aligned} \]

S4 和 Mamba 是连续系统的离散版本,包括一个时间尺度参数 \(\Delta\),用于将连续参数 \(\mathrm{A}、\mathrm{B}\) 转换为离散参数 \(\overline{\mathrm{A}}、\overline{\mathrm{B}}\)。常用的变换方法是零阶保持 (ZOH),定义如下:

\[ \begin{aligned} &\overline{\mathrm{A}}=\exp (\Delta \mathrm{A}),\\ &\overline{\mathrm{B}}=(\Delta \mathrm{A})^{-1}(\exp (\Delta \mathrm{A})-\mathrm{I}) \cdot \Delta \mathrm{B} . \end{aligned} \]

在对 \(\overline{\mathrm{A}}、\overline{\mathrm{B}}\) 离散化后,使用步长 \(\Delta\) 的公式 (1) 的离散版本可以重写为:

\[ \begin{aligned} h_t &=\overline{\mathbf{A}} h_{t-1}+\overline{\mathbf{B}} x_t, \\ y_t &=\mathrm{C} h_t . \end{aligned} \]

最后,模型通过全局卷积计算输出。

\[ \begin{aligned} \overline{\mathrm{K}} &=\left(\mathrm{C} \overline{\mathrm{B}}, \mathrm{C} \overline{\mathrm{AB}}, \ldots, \mathrm{C} \overline{\mathrm{A}}^{\mathrm{M}-1} \overline{\mathrm{B}}\right), \\ \mathrm{y} &=\mathrm{x} * \overline{\mathrm{K}}, \end{aligned} \]

其中 \(M\) 是输入序列 \(x\) 的长度,而 \(\bar{K} \in \mathbb{R}^M\) 是一个结构化卷积核。

3.2. Vision Mamba

图 2 给出了所提出的 Vim 的概览。标准的 Mamba 是为 1 维序列而设计的。为了处理视觉任务,我们首先将 2D 图像 \(\mathrm{t} \in \mathbb{R}^{\mathrm{H} \times \mathrm{W} \times \mathrm{C}}\) 转换为平铺的 2D 图像块 \(\mathrm{x}_\mathrm{p} \in \mathbb{R}^{\mathrm{J} \times(\mathrm{P}^2 \cdot \mathrm{C})}\),其中 \((\mathrm{H}, \mathrm{W})\) 是输入图像的大小,\(\mathrm{C}\) 是通道数,\(\mathrm{P}\) 是图像块的大小。接下来,我们将 \(\mathrm{x}_\mathrm{p}\) 线性投影到大小为 \(\mathrm{D}\) 的向量,并添加位置嵌入 \(\mathbf{E}_{\text {pos}} \in \mathbb{R}^{(\mathrm{J}+1) \times \mathrm{D}}\),如下所示:

\[ \mathbf{T}_0=\left[\mathbf{t}_{c l s} ; \mathbf{t}_p^1 \mathbf{W} ; \mathbf{t}_p^2 \mathbf{W} ; \cdots ; \mathbf{t}_p^{\mathrm{J}} \mathbf{W}\right]+\mathbf{E}_{p o s}, \]

其中 \(\mathrm{t}_p^{\mathrm{j}}\) 是 \(\mathrm{t}\) 的第 \(\mathrm{j}\) 个图像块,\(\mathrm{W} \in \mathbb{R}^{(\mathrm{P}^2 \cdot \mathrm{C}) \times \mathrm{D}}\) 是可学习的投影矩阵。受 ViT[13] 和 BERT[30] 的启发,我们也使用类别 token 来表示整个图像块序列,记为 \(\mathrm{t}_{cls}\)。然后我们将 token 序列 \((\mathrm{T}_{l-1})\) 送入 Vim 编码器的第 \(l\) 层,得到输出 \(\mathrm{T}_l\)。最后,我们对输出类别 token \(\mathrm{T}_\mathrm{L}^0\) 进行归一化处理,并将其送入多层感知器 (MLP) 头部以获得最终预测 \(\hat{p}\),如下所示:

\[ \begin{aligned} \mathrm{T}_l &=\operatorname{Vim}\left(\mathrm{T}_{l-1}\right)+\mathrm{T}_{l-1}, \\ \mathrm{f} &=\operatorname{Norm}\left(\mathrm{T}_{\mathrm{L}}^0\right), \\ \hat{p} &=\operatorname{MLP}(\mathrm{f}), \end{aligned} \]

其中 Vim 是所提出的视觉 mamba 块,L 是层数,Norm 是归一化层。

3.3. Vim 块

原始的 Mamba 块是为 1 维序列而设计的,不适用于需要空间感知理解的视觉任务。在这一节中,我们介绍了 Vim 块,它结合了双向序列建模,用于视觉任务。Vim 块如图 2 所示。

具体来说,我们在算法 21 中展示了 Vim 块的操作。输入的 token 序列 \(\mathbf{T}_{l-1}\) 首先由归一化层进行归一化。接下来,我们将归一化后的序列线性投影到维度大小为 E 的 \(\mathrm{x}\) 和 \(\mathrm{z}\)。然后,我们从正向和反向两个方向处理 \(\mathrm{x}\)。对于每个方向,我们首先对 \(\mathrm{x}\) 应用 1 维卷积,得到 \(\mathrm{x}_o^{\prime}\)。之后,我们将 \(\mathrm{x}_o^{\prime}\) 线性投影到 \(\mathrm{B}_o\)、\(\mathrm{C}_o\)、\(\Delta_o\) 分别。 \(\Delta_o\) 随后用于变换 \(\overline{\mathbf{A}}_o\)、\(\overline{\mathbf{B}}_o\)。最终,我们通过 SSM 计算 \(\mathbf{y}_{\text {forward}}\) 和 \(\mathbf{y}_{\text {backward}}\)。\(\mathbf{y}_{\text {forward}}\) 和 \(\mathrm{y}_{\text {backward}}\) 然后由 \(\mathrm{z}\) 进行门控并相加,得到输出 token 序列 \(T_l\)。

3.4. 架构细节

总结一下,我们架构的超参数如下所列:

L: 块的数量, D: 隐藏状态维数, E: 扩展状态维数, N: SSM 维数。

跟随 ViT [13] 和 DeiT [60],我们首先采用 \(16 \times 16\) 的核大小投影层获得一个由非重叠的 patch embedding 构成的 1 维序列。随后,我们直接堆叠 L 个 Vim 块。默认情况下,我们将块数 L 设置为 24,将 SSM 维数 N 设置为 16。为了与 DeiT 系列模型大小保持一致,我们将小型变体的隐藏状态维数 D 设置为 192,扩展状态维数 E 设置为 384。对于小型变体,我们将 D 设置为 384,将 E 设置为 768。

3.5. 效率分析

传统的基于 SSM 的方法利用快速傅里叶变换来加速公式 (4) 所示的卷积操作。对于数据相关的方法 (如 Mamba),算法 21 第 11 行的 SSM 操作不再等价于卷积。为解决此问题,Mamba 和所提出的 Vim 采用了一种现代硬件友好的方式来确保效率。这种优化的关键思想是避免现代硬件加速器 (GPU) 的 IO 约束和内存约束。

IO 效率。高带宽内存 (HBM) 和 SRAM 是 GPU 的两个重要组件。其中,SRAM 具有更大的带宽,而 HBM 具有更大的内存容量。使用 HBM 实现 Vim 的 SSM 操作的标准实现需要数量级为 O(BMEN) 的内存 IO 次数。受 Mamba 的启发,Vim 首先从速度较慢的 HBM 读取 O(BME+EN) 字节内存 (\(\boldsymbol{\Delta}_{\mathbf{o}}, \mathbf{A}_{\mathbf{o}}, \mathbf{B}_{\mathbf{o}}, \mathbf{C}_{\mathbf{o}}\)) 到快速 SRAM 中。然后,Vim 在 SRAM 中获得大小为 (B, M, E, N) 的离散 \(\overline{\mathbf{A}}_{\mathbf{o}}\)、\(\overline{\mathbf{B}}_{\mathbf{o}}\)。最后,Vim 在 SRAM 中执行 SSM 操作,并将大小为 (B, M, E) 的输出写回 HBM。该方法可以将 IO 次数从 O(BMEN) 减少到 O(BME+EN)。

内存效率。为了避免在处理长序列时出现内存不足问题并实现较低的内存使用,Vim 采用与 Mamba 相同的重计算方法。对于大小为 (B, M, E, N) 的用于计算梯度的中间状态,Vim 在网络反向传播时重新计算它们。对于诸如激活函数和卷积输出的中间激活值,Vim 也会重新计算它们以优化 GPU 内存需求,因为这些激活值占用大量内存,但重新计算速度很快。

计算效率。Vim 块中的 SSM(算法 21 第 11 行) 和 Transformer 中的自注意力在自适应地提供全局上下文时都扮演着关键角色。给定一个视觉序列 \(T \in R^{1 \times M \times D}\) 和默认设置 \(E=2D\),全局自注意力和 SSM 的计算复杂度为:

\[ \begin{aligned} &\Omega(\text{self-attention})=4\mathrm{MD}^2+2\mathrm{M}^2\mathrm{D},\\ &\Omega(\mathrm{SSM})=3\mathrm{M}(2\mathrm{D})\mathrm{N}+\mathrm{M}(2\mathrm{D})\mathrm{N}, \end{aligned} \]

其中自注意力对序列长度 M 的复杂度是二次的,而 SSM 对序列长度 M 的复杂度是线性的 (N 是固定参数,默认设为 16)。这种计算效率使 Vim 能够扩展到针对大序列长度的千兆像素应用。

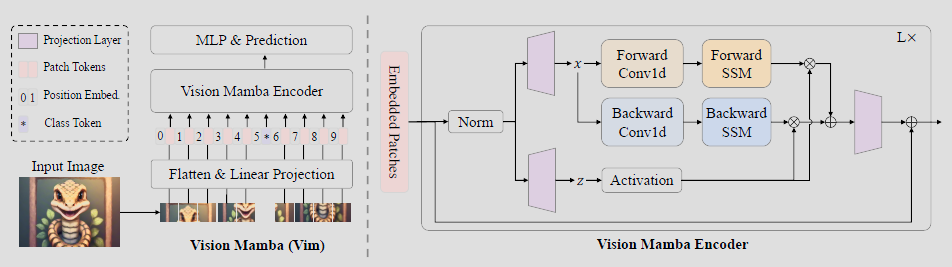
图 2. 所提出的 Vim 模型概览。我们首先将输入图像分割为图像块,然后将它们投影为 patch token。最后,我们将 token 序列送入所提出的 Vim 编码器。为执行 ImageNet 分类,我们将一个额外的可学习分类 token 连接到 patch token 序列。不同于用于文本序列建模的 Mamba,Vim 编码器使用正向和反向两个方向处理 token 序列。