Vision Transformer (四)
Attention
原文地址:https://zhuanlan.zhihu.com/p/354913120
Transformer 是 Google 的团队在 2017 年提出的一种 NLP 经典模型,现在比较火热的 Bert 也是基于 Transformer。Transformer 模型使用了 Self-Attention 机制,不采用 RNN 的顺序结构,使得模型可以并行化训练,而且能够拥有全局信息。
本文分析的文章都是针对 Transformer 内部机制的探究,从而提出的对于 ViT,DeiT 模型的改进。第 1 篇是针对 Transformer 模型处理图片的方式:将输入图片划分成一个个块 (patch),然后针对将这些 patch 看成一个序列 (Sequence) 的不完美之处,提出了一种 TNT 架构,它不仅考虑 patch 之间的信息,还考虑每个 patch 的内部信息,使得 Transformer 模型分别对整体和局部信息进行建模,提升性能。第 2 篇 CPVT 通过 PEG 模块代替传统的位置编码,实现了灵活的位置表示和更高效的位置信息编码,提升了 DeiT/ViT 的性能。值得一提的是,这 2 种方法与其他的改进措施是正交的,可以在不相互影响的条件下直接完成迁移。
对本文符号进行统一:
Multi-head Self-attention:
\(\begin{equation} \textit{Attention}(Q,K,V) = \textit{softmax}(\frac{QK^T}{\sqrt{d_k}})V. \end{equation}\)
式中, \(X\in\mathbb{R}^{n\times d}\) , \(Q\in\mathbb{R}^{n\times d_k}\) , \(K\in\mathbb{R}^{n\times d_k}\) , \(V\in\mathbb{R}^{n\times d_v}\) , \(n\) 代表序列长度, \(d,d_k,d_v\) 代表 hidden dimension。
MLP 层:
式中, \(W_1\in\mathbb{R}^{d\times d_m}, W_2\in\mathbb{R}^{d_m\times d}\) 为 2 个 FC 层的权重, \(b_1\in\mathbb{R}^{d_m},b_2\in\mathbb{R}^{d}\) 是 bias 值。
Layer Normalization:
LN 层是 Transformer 模型快速训练和稳定收敛的重要保证。LN 层的作用对象是 \(x\in\mathbb{R}^{d}\) , \(\mu\in\mathbb{R},\delta\in\mathbb{R}\) 代表每个样本的均值和方差。 \(\gamma\in\mathbb{R}^{d},\beta\in\mathbb{R}^{d}\) 是可学习的仿射参数。
9 充分挖掘 patch 内部信息:Transformer in Transformer:TNT¶
论文名称:Transformer in Transformer
论文地址:
https://arxiv.org/pdf/2103.00112.pdf
- 9.1 TNT 原理分析:
Transformer 网络推动了诸多自然语言处理任务的进步,而近期 transformer 开始在计算机视觉领域崭露头角。例如,DETR 将目标检测视为一个直接集预测问题,并使用 transformer 编码器 - 解码器架构来解决它;IPT 利用 transformer 在单个模型中处理多个底层视觉任务。与现有主流 CNN 模型(如 ResNet)相比,这些基于 transformer 的模型在视觉任务上也显示出了良好的性能。其中,将 Transformer 应用在图像识别领域的两个经典的工作是:ViT 和 DeiT(详细的解读进入链接查看)。ViT 的结构如下图 1 所示。它先将输入图片划分成一个个块 (patch),然后将这些 patch 看成一个块的序列 (Sequence),这里假设序列长度为 \(N\) 。再把这个序列中的每个 patch 进行展平操作 (Flatten),这样一来,每个 patch 就转化成了一个向量,我们假设这个向量是 \(c\) 维的。那么经过以上所有操作,一张输入图片就成为了一个大小为 \((N,c)\) 的矩阵。这个矩阵与一个向量 \(\color{purple}{\text{class token}}\) 一起被输入 Transformer 的 Encoder 中,来处理图像 patch 序列,最终由 \(\color{purple}{\text{class token}}\) 的输出做图像识别。
DeiT 对 ViT 的结构做了一点微小的改动,输入图片依然经过相同的操作变成一个大小为 \((N,c)\) 的矩阵,只是此时这个矩阵与一个向量 \(\color{purple}{\text{class token}}\) 和另一个向量 \(\color{crimson}{\text{distillation token}}\) 一起被输入 Transformer 的 Encoder 中,来处理图像 patch 序列。在训练时,对 \(\color{purple}{\text{class token}}\) 的输出使用有监督损失,对 \(\color{crimson}{\text{distillation token}}\) 的输出使用蒸馏损失。最终由 \(\color{purple}{\text{class token}}\) 的输出和 \(\color{crimson}{\text{distillation token}}\) 的输出的均值做图像识别。
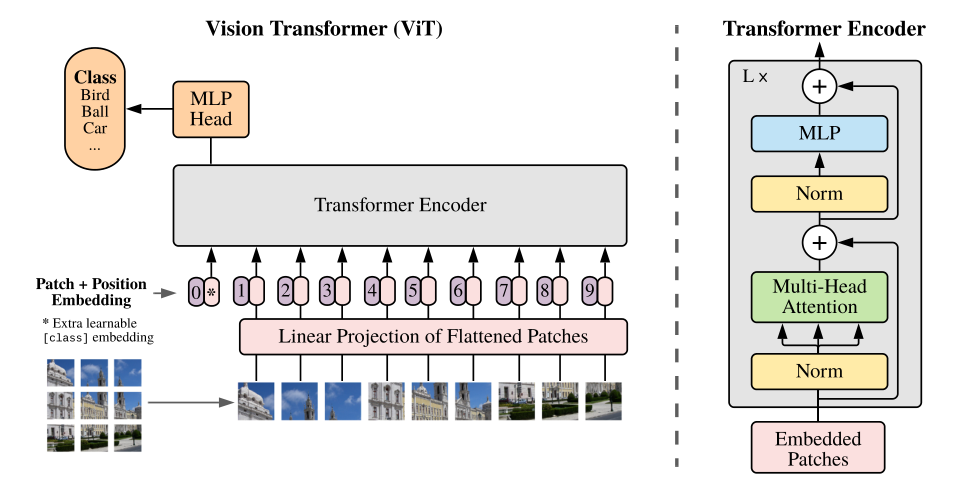
到这里我们发现,DeiT 相比于 ViT 来讲,在训练方式上做出了改进,这使得 Transformer 在建模 patch 之间的信息时考虑更多的因素,提升了 Transformer 模型的整体性能。但是,DeiT 有一个没有解决的问题是:
DeiT 依然把图片转化成 patch 并进行 Flatten 操作之后输入 Transformer 模型,而这种转化成 patch 的办法,真的是处理图片这种 2D 输入信息的最合适的方法吗?
我们知道,Transformer 需要的是序列 (Sequence) 的输入信号,而我们有的是 image 这种 2D 的输入信号,那直接把图片分块以后进行 Flatten 操作是一种很直觉的处理方式。但是,这种 intuitive 的方法能不能够完美地建模图像呢?
答案显然是否定的。因为我们缺少了一部分非常重要的信息,即:每个 patch 的内部信息。
问:为什么每个 patch 的内部信息这么重要?
答:Transformer 这种模型之所以有效,是因为它能处理长度为 \(N\) 的输入序列中这 \(N\) 个输入之间的关系 (relationship),而对于每个输入的内部信息的 relationship,它是无能为力的,因为 ViT,DeiT,IPT,SETR,ViT-FRCNN 这类模型把每个 patch 展平为了一个向量,破坏了每个 patch 的内部信息。
所以我们认为,每个输入的内部信息,即每个 patch 的内部信息,没有被 Transformer 所建模。是一个欠考虑的因素。
所以本文的动机是:使得 Transformer 模型既建模那些不同 patch 之间的关系,也要建模每个 patch 内部的关系。
所以作者这里设计了一种 Transformer in Transformer (TNT) 的结构,第 1 步还是将输入图片划分成 \(n\) 个块 (patch):
式中 \(p\) 是每个块的大小。ViT,DeiT,IPT,SETR,ViT-FRCNN 到这里就把它们输入 Transformer 了,本文为了更好地学习图片中 global 和 local 信息的关系,还要再进行一步:
接下来再把每个 patch 通过 PyTorch 的 unfold 操作划分成更小的 patch,之后把这些小 patch 展平,就得到了
式中 \(Y_0^i\in\mathbb{R}^{p'\times p'\times c}, i=1,2,\cdots,n\) ,那么 \(Y_{\color{orange}{0}}^{\color{green}{i}}\) 代表的物理意义是第 \(\color{orange}{0}\) 个 layer 的第 \(\color{green}{i}\) 个大 patch 包含的所有小 patch, \(c\) 是 channel 数。意思是:原图是 \(\mathcal{Y}_0\) ,分成 \(n\) 个大 patch,每个大 patch 可以看做是由很多 \(p'\times p'\) 的小 patch 组成的。
例如,大 patch 的大小是 \(16\times16\times3\) ,这里 \(p=16\) ,那么小 patch 的大小是 \(8\times8\times3\) 。每个大 patch 被分成了 4 个小 patch,即 \(Y_{\color{orange}{0}}^{\color{green}{i}}\in\mathbb{R}^{8\times 8\times 12}\) 相当于是 4 个小 patch。
接下来作者把 \(Y_{\color{orange}{0}}^{\color{green}{i}}\in\mathbb{R}^{p'\times p'\times c}\) 这一堆小 patch 视为一个 pixel embedding:
这个 pixel embedding 由 \(m=p'^2\) 个向量组成,每个向量 \(y_0^{i,j}\in\mathbb{R}^{c}, j=1,2,\cdots,m\) 。
如下图 2 所示,输入是一个大 patch,输出的黄色大长条是这个 patch 展平以后的 patch embedding,输出的彩色小长条是这个 patch 划分成更小的 patch 之后再展平以后的 pixel embedding。
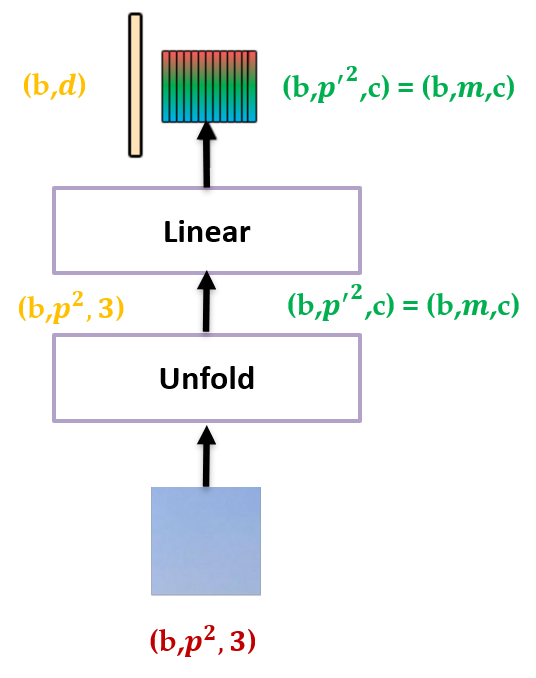
图 2 的操作进行完之后就得到了大 patch 的 patch embedding 以及小 patch 的 pixel embedding。接下来把它们送入 Transformer 的 Block 里面建模特征,如下图 3 所示。Transformer 是由很多 TNT Blocks 组成的,每个 TNT Block 包含 2 个 Transformer Block,分别是:
- Outer block 建模 patch embedding 之间的 global relationship。
- Inner block 建模 pixel embedding 之间的 local structure information。
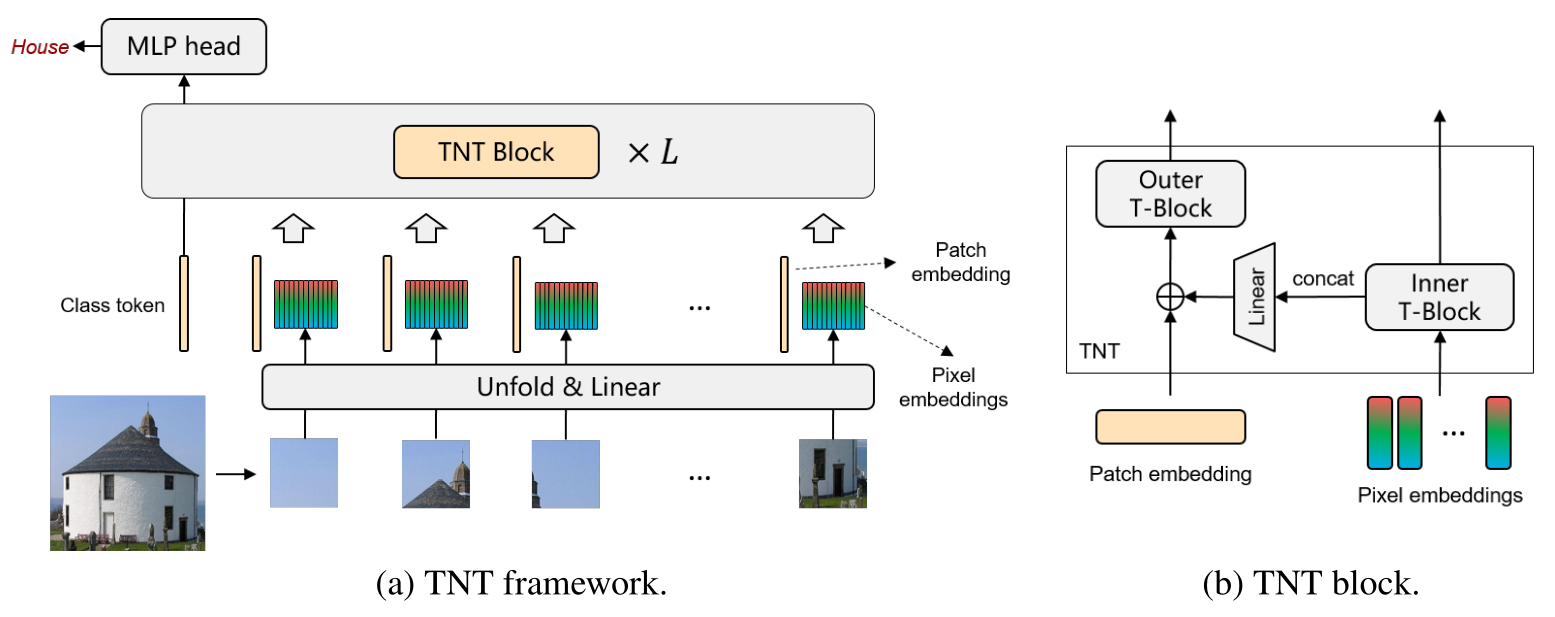
这两种 Block 对应 2 个不同的数据流,其中 Outer block 的数据流在不同 patch 之间运行,而 Inner block 的数据流在每个 patch 内部运行。
Inner Transformer:
定义 \(Y_l^i \in\mathbb{R}^{p'\times p'\times c}=\mathbb{R}^{m\times c}\) ,我们把这个值传入 Inner Transformer \(T_{in}\) ,则有:
注意正常的 Transformer 的输入应该是 \((b,n,d)\) 的张量,这里 \(b\) 代表 batch size, \(n\) 代表序列长度, \(d\) 代表 hidden dimension。不考虑 batch size 这一维,就是一个 \((n,d)\) 的矩阵,也可以看做是 \(n\) 个 \(d\) 维向量,那么对于 Inner Transformer \(T_{in}\) 来讲,这里的 \(d=mc\) 。也就是说,Inner Transformer \(T_{in}\) 的输入是 \(n\) 个 \(mc\) 维的向量。注意这里的 \(Y_l^i \in\mathbb{R}^{p'\times p'\times c}=\mathbb{R}^{m\times c}\) 就是这 \(n\) 个向量的其中一个。所以 Inner Transformer 的第 \(l\) 个 layer 的输出就可以写为:
Inner Transformer \(T_{in}\) 建模的是更细小的像素级别的 relationship,例如,在一张人脸中,属于眼睛的像素与眼睛的其他像素更相关,而与前额像素的 relationship 较少。
Outer Transformer:
Outer Transformer \(T_{out}\) 就相当于是 ViT 中的 Transformer,它建模的是更答大的 patch 级别的 relationship,输入的 patch embedding 使用 ViT 类似的做法,添加 \(\color{purple}{\text{class token}}\;Z_\text{class}\) ,它们初始化为 0。
定义 \(\mathcal{Z}_l^i\in\mathbb{R}^{d}\) 为第 \(l\) 个 layer 的第 \(i\) 个向量,则 Outer Transformer 的表达式为:
那么现在既有 Outer Transformer 的第 \(l\) 个 layer 的输出向量:
也有 Inner Transformer 的第 \(l\) 个 layer 的输出向量:
下面的问题是:要如何把它们结合起来,以融合 global 和 local 的信息呢?
作者采用的方式是:
式中, \(Z_{l-1}^i\in\mathbb{R}^{d},\textit{Vec}(\cdot)\) 代表 Flatten 操作, \(W_{l-1}\in\mathbb{R}^{mc\times d},b_{l-1}\in\mathbb{R}^{d}\) 代表权重。
通过这种方式,把第 \(l\) 个 layer 的第 \(i\) 个 patch embedding 向量和第 \(i\) 个 pixel embedding 向量融合起来,即对应图 3(b) 的结构。
总的来说,TNT Block 第 \(l\) 个 layer 的输入和输出可以表示为:
在 TNT Block 中,Inner Transformer 建模 pixel embedding 之间的 local structure information 之间的关系,而 Outer block 建模 patch embedding 之间的 global relationship。通过将 TNT Block 堆叠 \(L\) 次,作者构建了 Transformer in Transformer。最后,使用一个分类头对图像进行分类。
位置编码:
位置编码的作用是让像素间保持空间位置关系,对于图像就是保持二维信息,它对于图像识别任务来讲很重要。具体来说,就需要对 patch embedding 和 pixel embedding 分别设计一种位置编码。
- patch positional encoding:
作者这里使用的是可学习的 1D 位置编码:
式中, \(E_{patch}\in\mathbb{R}^{(n+1)\times d}\) 是给 patch embedding 使用的位置编码,它用来编码全局空间信息 (global spatial information)。
- pixel positional encoding:
作者这里使用的是可学习的 1D 位置编码:
式中, \(E_{pixel}\in\mathbb{R}^{m\times c}\) 是给 pixel embedding 使用的位置编码。我们发现这 \(n\) 个 patch 中的 pixel positional encoding 是一样的,它们用来编码局部相对信息 (local relative information)。
计算复杂度分析,标准的 Transformer Block 的结构:
一个标准的 Transformer Block 的结构包括 multi-head self-attention (MSA) 和 multi-layer
perceptron (MLP)。
MSA 的计算复杂度是:
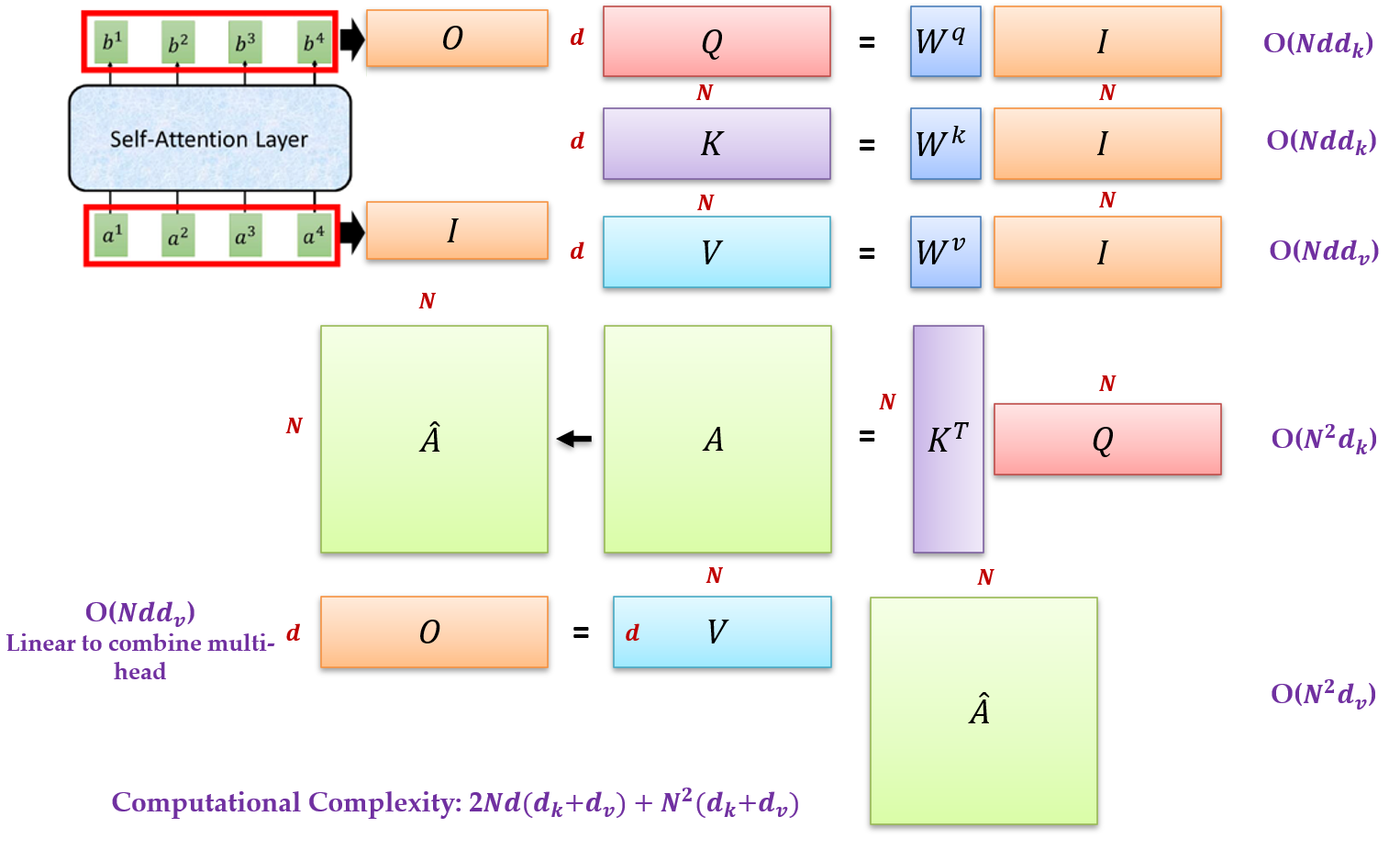
MLP 的计算复杂度是:
式中, \(r\) 是 expansion ratio。
所以一个标准的 Transformer Block 的计算复杂度是:
\(r\) 经常设置为 4,且 \(d_k\) 和 \(d_v\) 一般是相等的,所以:
一个标准的 Transformer Block 的参数量为: \(12dd\) 。
计算复杂度分析,TNT Block 的结构:
\(T_{in}\) 的计算复杂度: \(2nmc(6c+m)\)
\(T_{out}\) 的计算复杂度: \(2nd(6d+n)\)
Linear Transformation 的计算复杂度是: \(nmcd\)
所以一个标准的 TNT Block 的计算复杂度是:
一个标准的 TNT Block 的参数量为:\(\text { Params }_{T N T}=12 c c+m c d+12 d d .\)
看似 TNT 相比于标准的 Transformer 结构的计算量和参数量都增加了很多,但是实际上并没有增加多少。因为这里的: \(c\ll d\) 。
比如在 ViT-B/16 configuration 中,设置: \(d=768,n=196,c=12,m=64\) ,则:
\(\mathrm{FLOPs}_{T}=1446M, \mathrm{FLOPs}_{TNT}=1603M\) ,增长了大概 1.09 倍,同样地,参数量增长了大概 1.08 倍。通过少量增加计算和内存成本,TNT Block 可以有效地模拟局部结构信息,并在准确性和复杂性之间实现更好的平衡,如实验所示。
网络架构:
超参数设置为:
大 patch 的 patch size:16×16,小 patch 的 patch size:4×4,设计了 2 种不同大小的 TNT 模型,分别是:TNT-S 和 TNT-B,模型的参数量大小分别是 23.8M 和 65.6M。计算量分别是 5.2B 和 14.1B。

作者还使用了 SE 模块进行 channel-wise 的 attention,具体来讲,把每个 patch 的 d 个 channel 的 embedding 做平均操作,经过一个 2 层的 MLP 得到 d 个 attention values。这 d 个 attention 会对应地乘在 d 个 channel 上面。SE 模块的好处是仅仅增大了一点参数但却能通过 dimension-wise attention 实现特征的增强。
Experiments:
Dataset:
数据集如下图 6 所示,除了 ImageNet 以外,下面几行的小数据集用作迁移学习。数据增强方式包括了:random crop, random clip, Rand-Augment, Mixup 和 CutMix。
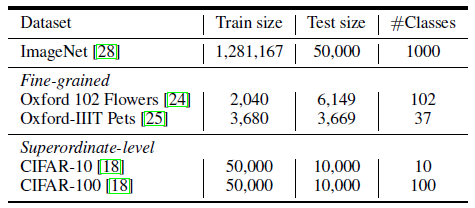
训练的方式如下图 7 所示:

实验 1:ImageNet 结果:
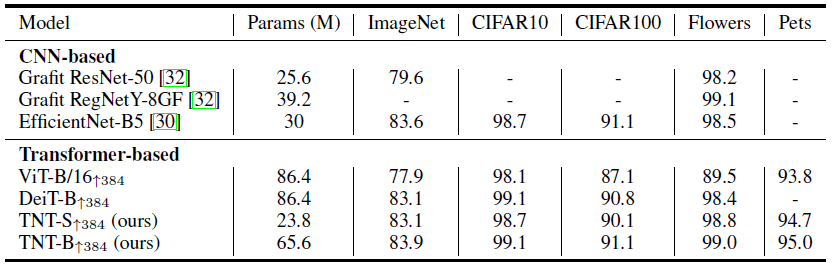
作者比较了 TNT 与基于 Transformer 的 ViT 和 DeiT 模型,以及几个具有代表性的 CNN 模型比如 ResNet,RegNet 和 EfficientNet,结果如图 8,9 所示。
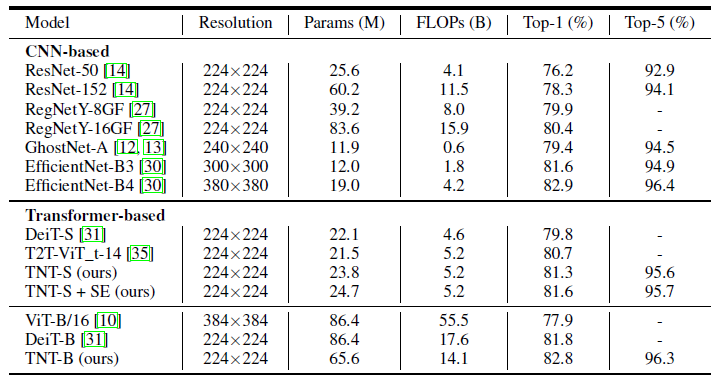
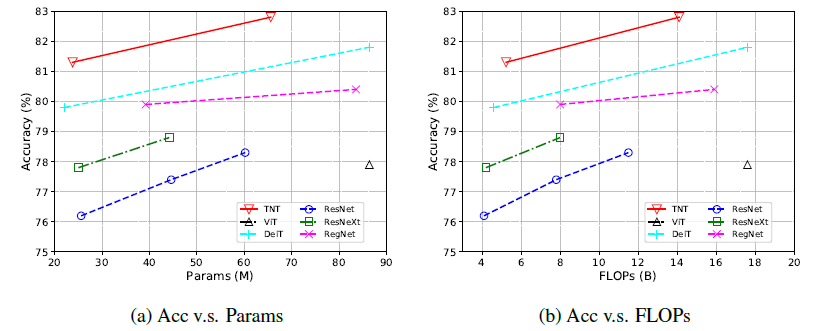
结果表明,TNT 超过了所有的基于 Transformer 的分类模型,TNT-S 模型达到了 81.3% 的精确度,在与 DeiT-S 参数量相当的前提下提升了 1.5%,再次证明了 local structure information 的重要性。再通过添加 SE 模块,TNT 可以达到 81.6% 的性能,也超过了基于卷积的 ResNet 和 RegNet。
对比实验 1:位置编码的影响
位置编码在图像识别任务中的作用还是挺大的,因为它让像素间保持空间位置关系,对于图像就是保持二维信息。比如一个像素点的前后左右,直接 flatten 之后进行 self-attention 的结果和左右前后 flatten 之后进行 self-attention 的结果其实是一样的。所以如果没有位置编码,就没法建模这个前后左右的位置信息。patch position encoding 的目的是存储全局空间信息,而 pixel position encoding 的目的是存储局部相对信息。如下图 10 所示,去掉位置编码之后会带来一定程度的 accuracy drop。
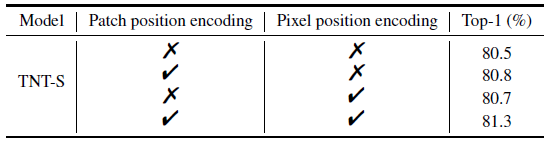
对比实验 2:head 数量的影响
head 数量适中 (2, 4) 时能达到比较好的性能。

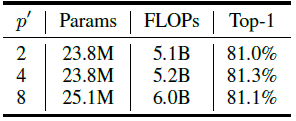
对比实验 3:小 patch size 的影响
TNT 模型先和 ViT 一样的做法,把图片划分为 16×16 的 patch,再进一步把这些 patch 使用 unfold 操作变成 \(p^{'}\times p^{'}\) 的小 patch,从图 12 的结果可以发现, \(p^{'}\) 的取值对最终的结果影响不大,考虑到模型的大小和计算量,最终选择了 \(p^{'}=4\) 。
实验 2:可视化
作者可视化了 DeiT 和 TNT 的 learned feature maps,具体是先把输入 resize 成 1024×1024,那么第 1,6,12 个 Block 的输出的特征维度是 64×64×d。从 d 个特征里面随机采样 12 个 feature map 得到图 13。DeiT 也采用相同的操作,与 DeiT 相比较而言,TNT 更好地保持了 local information。作者还是用 T-SNE 可视化了 Block 12 输出的所有 384 (Outer Transformer dim) 个 feature maps,可以看到, TNT 的特征比 DeiT 更丰富,包含的信息也更丰富。这些好处归功于 Inner Transformer 的引入,以建模局部特征。

除了 patch level 的特征以外,作者还可视化了 pixel level 的信息,如下图 14 所示。pixel embedding 的维度是 (b, 64, c),把 64 这个维度 reshape 成 8×8 的小 patch,可以得到 14×14 个。
作者将 Block 1,6,12 的输出的这 14×14 个 patch 在 c 维度上进行求平均的结果打印出来,发现 shallow layer 很好地保留了局部信息,而随着网络的深入,表示逐渐变得更加抽象。

实验 3:迁移学习
作者为了证明 TNT 的泛化性能,将 TNT-S,TNT-B 这 2 个模型迁移到了小数据集 (CIFAR-10, CIFAR-100, Oxford-IIIT Pets, Oxford 102 Flowers) 上面。所有模型都使用了 384×384 的数据 fine-tune。如图 15 所示,我们发现 TNT 在大多数数据集的参数较少时优于 DeiT ,这表明了建模像素级关系以获得更好的 feature representation 的优越性。fine-tune 时为了在不同的分辨率中微调,作者还对位置编码进行了插值。
10 探究位置编码的必要性:Do We Really Need Explicit Position Encodings for Vision Transformers?¶
论文名称:Do We Really Need Explicit Position Encodings for Vision Transformers?
论文地址:
https://arxiv.org/pdf/2102.10882.pdf
- 10.1 CPVT 原理分析:
self-attention 这种结构的特点是可以建模一整个输入序列的信息,并能根据图片的内容来动态调整感受野,但是 self-attention 的缺点是:排列不变性 (permutation-invariant),即:无法建模输入序列的顺序信息,输入这个序列顺序的调整是不会影响输出结果的。为了解决这个问题,Transformer 引入了位置编码机制。位置编码在图像识别任务中的作用还是挺大的,因为它让像素间保持空间位置关系,对于图像就是保持二维信息。比如一个像素点的前后左右,直接 flatten 之后进行 self-attention 的结果和左右前后 flatten 之后进行 self-attention 的结果其实是一样的。所以如果没有位置编码,就没法建模这个前后左右的位置信息。位置编码可以设置为可学习的,也可以设置为不可学习的正弦函数。
但是,位置编码的缺点是:它的长度往往是固定的。比如输入图片的大小是 \(H\times W\) ,分成大小为 \(S\times S\) 的 patch,那么 patch 的数量就是 \(N = \frac{HW}{S^2}\) 。比如现在训练集输入图片是 224×224 的,分成大小为 16×16 的 patch,那么序列长度是 196。所以训练时把位置编码的长度也设置为 196。但是后续进行迁移学习时输入图片是 384×384 的,分成大小为 16×16 的 patch,那么序列长度是 576。此时你的长度是 196 的位置编码就不够了,这时人们通常的做法有这么几种:
1. 去掉位置编码
会严重地影响分类性能,因为输入序列的位置信息丢失了。以 DeiT-tiny 为例,不使用位置编码会使性能从 72.2% 降为 68.2%。
2. 相对位置编码
相对位置编码的相关工作有以下几个:
Relative Position Encoding 考虑 sequence 元素之间的距离,也是一种有效的手段。
https://arxiv.org/pdf/1803.02155.pdf
2D 相对位置编码:
https://arxiv.org/pdf/1904.09925.pdf
相对位置编码的表达式如下:
式中, \(a_{ij} \in \mathbb{R}^{d_k}\) 是:当把输入 sequence 视为有向的全连接的图时 \(x_i\) 和 \(x_j\) 的 edge distance。
这种做法的缺点是实现起来比较复杂,不够 efficient,因为需要改变 Transformer 内部的表达式。
3. 插值法
把位置编码进行双三次插值 (bicubic interpolation),把 196 的位置编码插值成长度为 396 的,以适应新的数据集。
即便是有这样的补救措施,但是:
- 许多视觉任务都需要不断改变输入图片的大小,也就需要不断改变输入序列的长度,这样做很不方便。
- 插值的方法会影响性能。
以上这 3 种办法的性能的比较如下图所示,结果发现:在使用位置编码的情况下,无论是使用可学习的位置编码 (learnable),还是固定的位置编码 (sin-cos),其训练的模型性能是差不多的。但是使用相对位置编码后性能会有下降,不使用位置编码性能会大幅下降。证明位置编码对于 Vision Transformer 的重要性。
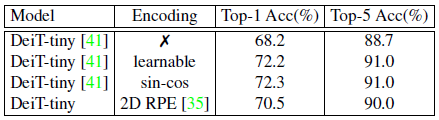
所以目前面临的问题就是:我们需要一种新的位置编码策略,既能解决传统位置编码不可变长度的局限性,又能起到位置编码的作用。
本文就是为了解决这个问题,即:灵活地把位置信息引入 Transformer 中。之前工作的位置编码一般是预定义好并与输入无关 (predefined and inputagnostic),本文的位置编码是即时的 (on-the-fly),就是需要多长的编码就立刻有多长的编码。
这种方法取名为 CVPT,如下图 17 所示。CVPT 能自动生成一种包含位置信息的编码 PEG,提升 Transformer 模型的性能。通过这样做,Transformer 可以处理任意大小的输入图像,而无需双三次插值。
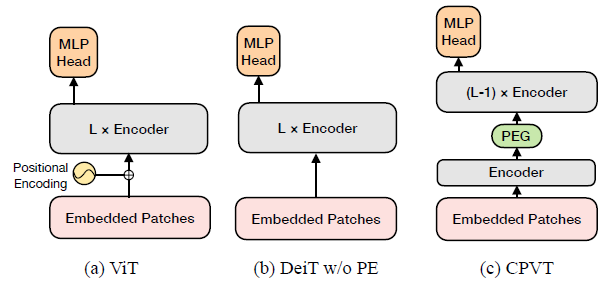
其实对于 Positional Encoding 的研究之前已有一些:CNN 操作看上去没有进行卷积操作,但是实际上却能够隐含地编码绝对位置信息。具体来说,zero padding 和 borders 其实扮演了一种 anchor 的角色,以获取空间信息。关于这个研究可以参考下面的 2 个链接:
Xinlong Wang:CNN 是怎么学到图片内的绝对位置信息的?https://arxiv.org/pdf/2101.12322.pdf
CoordConv 使用 concatenation 代替 Transformer 中的位置编码的加法操作。
https://arxiv.org/pdf/1807.03247.pdf
Relative Position Encoding 考虑 sequence 元素之间的距离,也是一种有效的手段。
https://arxiv.org/pdf/1803.02155.pdf
2D 相对位置编码:
https://arxiv.org/pdf/1904.09925.pdf
LambdaNetwork 使用 Lambda layers 来建模长距离的内容和位置信息的 interactions,这样就可以避免使用 self-attention layer。LambdaNetwork 的实验证明: 位置信息的 interaction 对于性能的提升是必要的,而基于内容的 interaction 只能带来性能的小幅度的改善。
Transformer 的位置编码表达式为:
式中, \(pos\) 代表某个词在序列中的位置, \(d_{\text{model}}\) 代表这个 Transformer 模型的 embedding dimension。 \(i\) 代表当前的 dimension,取值范围是: \([0,\frac{d_{\text{model}}}{2})\) 。
回到 CVPT 上来,它的 motivation 说:一个好的位置编码应该具备以下 3 个特征:
- 继续保持很强的性能。
- 能够避免排列不变性 (permutation equivariance),即:输入序列的顺序变化时,结果也不同,能起到位置编码的作用。且随着输入 size 的改变要也可以灵活地变化。
- 高效,易于实现。不改变原版 Transformer 的公式。
CVPT 的 Positional Encoding Generator (PEG) 的具体做法是:
先把输入 \(X \in \mathbb{R}^{B\times N\times C}\) reshape 回 2D 的张量 \(X' \in \mathbb{R}^{B\times C \times H \times W}\) 。
再把 \(X'\) 通过 2D 的 Transformation \(\mathcal{F}\) 并把输出再变为 \(X'' \in \mathbb{R}^{B \times N \times C}\) 。 \(\mathcal{F}\) 具体是个卷积,卷积核 \(k (k\geq3)\) ,zero-padding \(\frac{k-1}{2}\) ,这样不改变 spatial resolution。
class token \(Y \in \mathbb{R}^{B \times C}\) 保持不变。
最后把 \(Y\) 和 concatenate 起来,得到 PEG 输出。
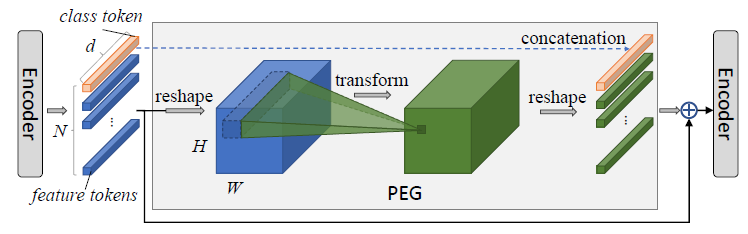
问:为什么要这么做?这种做法怎么就能把位置信息引入 Transformer 了?
答:给 Transformer 引入位置信息,说白了就是给一个 sequence 的 \(N\) 个向量 assign a position。那这个 position 它既可以是绝对信息,也可以是相对信息。相对信息就是定义一个参考点然后给每个向量一个代表它与参考点相对位置的信息。这种做法相当于是使用卷积操作得到 positional encoding,而卷积操作的 zero-padding 就是相当于是参考点,卷积操作相当于提取了每个向量与参考点的相对位置信息。所以这种办法用一句话概括就是:
PEG 的卷积部分以 zero-padding 作为参考点,以卷积操作提取相对位置信息,借助卷积得到适用于 Transformer 的可变长度的位置编码。
我们通过下面的可视化结果来看下位置编码的影响:
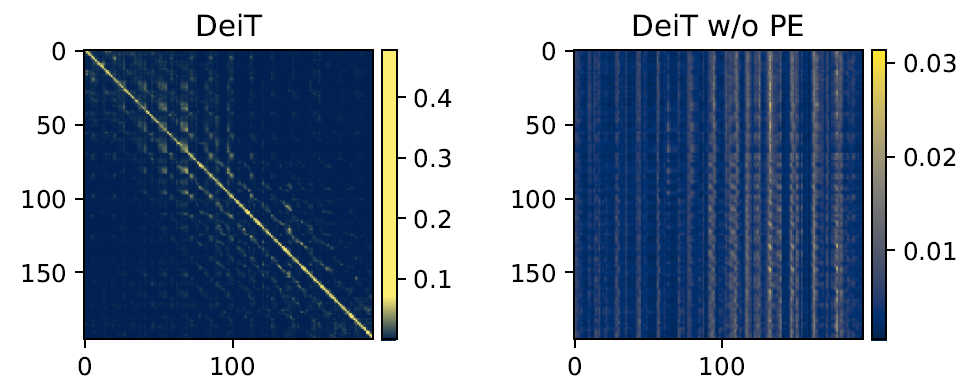
考虑一张 224×224 的 image,分成 14×14 个 patch。我们使用一个 196×196 的矩阵来表示这 196 个 patch 之间的 self-attention score,如下图 19 所示。左边是 DeiT 的结果,右边是 DeiT 去掉位置编码的结果。我们发现 DeiT 学到了 a schema of locality。每个 patch 只与它的 local neighbor interacts strongly,与那些距离它很远的 patch interacts weakly。但是去掉位置编码以后,这种 schema 消失了,每个 patch 与它的 neighbor 变得没有联系了,位置信息也消失了。
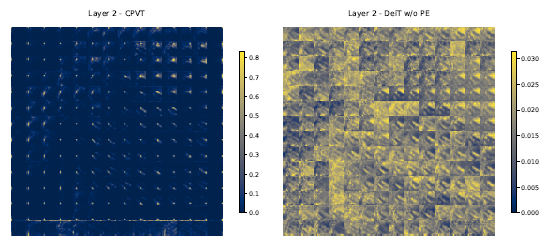
下图 20 是使用 CPVT 以后第 2 个 encoder block 的输出的 attention maps,把上一张图的每一行 (196×1) reshape 到了 14×14 的格子,一共有 196 个格子。最左上方的格子关注 (attention) 的点在左上,而最左下方的格子关注 (attention) 的点在左下,以此类推,所以 CPVT 依然能够学习到 local information。
Experiment:
数据集:ImageNet
模型 variants:
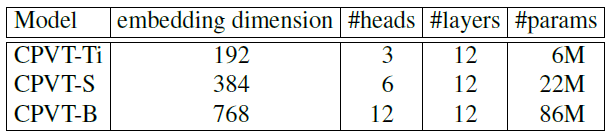
8 卡 V100 跑 CPVT-Tiny,Small,Base 模型分别需要 1.3days,1.6days 和 2.5days。
Training details:
300 epochs,batch size=2048,AdamW。超参数与 DeiT 保持一致。
学习率的变化公式: \(lr_{scale} = \frac{0.0005* Batch Size_{global}}{512}\)
实验 1:ImageNet 与 SOTA 的对比:
CPVT 在模型参数和计算量一致的前提下比 DeiT 的性能有所提升。
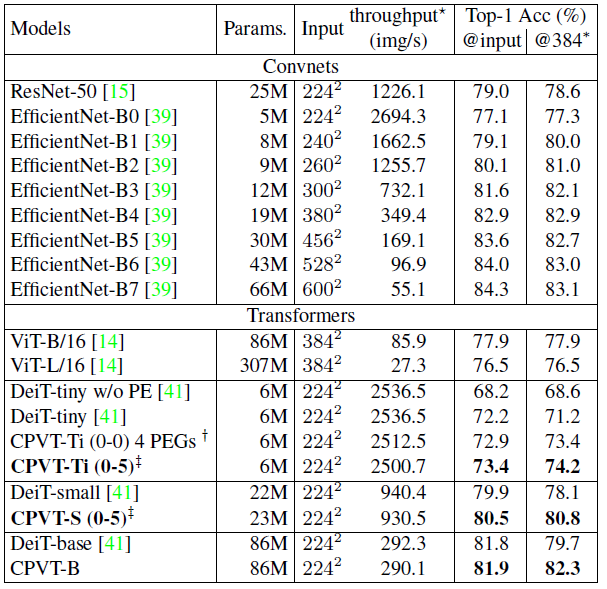
值得一提的是,这个表格的最右侧一列是在 224×224 的数据集上训练好的模型直接在 384×384 的数据集上测试,而不进行任何 fine-tuning 的结果。作者发现 DeiT-tiny 的性能从 72.2% 降为了 71.2%,而 CVPT 的性能却从 73.4% 上升到了 74.2%,证明了 CVPT 方法对于数据集大小变化的适应性。它不需要任何其他的措施来适应这一变化,仅靠着一层网络来适应数据集尺寸的变化。
实验 2:目标检测任务性能:
作者又对 Transformer 做检测任务的 DETR 模型使用了本文的 PEG 模块,epochs 数量从 500 降为 50,优化器是 AdamW,batch size 为 32,weight decay 为 0.0001。backbone 和 Trasnformer 的初始 learning rate 分别为 \(2\times10^{-5}\) 和 \(1\times10^{-4}\) 。learning rate 使用 stepLR 策略,在 epoch 为 40 是降为 0.1 倍。实验结果如图 23 所示。为了对比的公平 DETR 和 Deformable-DETR 都使用了 sine positional encoding。如果去掉位置编码,DETR 的 mAP 从 33.7% 降为 32.8%;但如果使用了本文的 PEG 模块会提升至 33.9%。Deformable-DETR 也得到了相似的实验结果,证明 PEG 优于原本的 positional encoding。
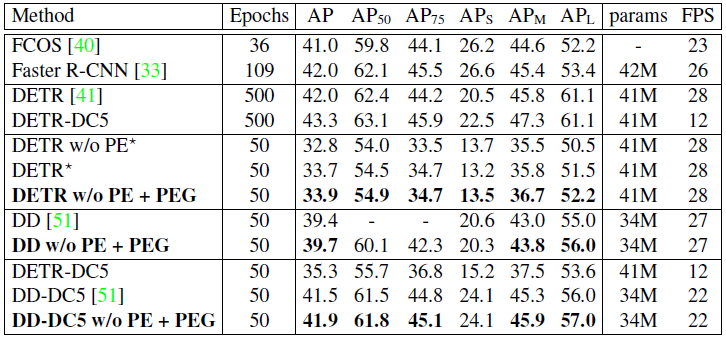
实验 3:PEG 复杂度分析:
参数量:
这一部分主要来看看 PEG 这个模块为模型引入了多少额外的参数量和计算量。我们假设 Transformer 模型的 embedding dim 为 \(d\) ,如果只使用 \(l\) 个 Depthwise convolution,增加的参数量是 \(dlk^2\) ,如果使用 \(l\) 个 Depthwise Separable convolution,增加的参数量是 \(dlk^2+ld^2\) 。当 \(k=3,l=1\) 时,CVPT-Ti 模型的 \(d=192\) 带来大约 \(1728\) 的参数。而 DeiT-Tiny 的位置编码参数量为 \(14\times14\times192=37632\) ,所以 CVPT-Ti 节约了大约 \(37632-1728=35904\) 个参数。即便你使用 Depthwise Separable convolution,PEG 参数量为 \(192^2+9\times192=38592\) ,相比原来的 \(37632\) 只多了 960 个参数,可以忽略不计。
计算量:
\(l\) 层 Depthwise convolution 的计算量是 \(14\times14dlk^2\) ,当 \(k=3,l=1\) 时计算量大概是 \(196\times192\times9=0.34M\) ,相比 Tiny 模型 2.1G 的计算量来说可以忽略。
对比实验 1:PEG 模块插入策略比较
作者对比了几种不同的插入策略,图中的 LE 代表 learnable encoding,RPE 代表 relative positional encoding,sin-cos 代表 absolute positional encoding。
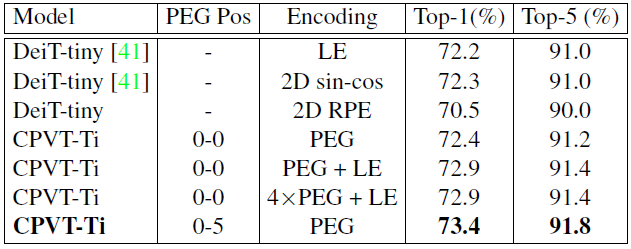
结论:
sin-cos 和可学习的位置编码差别不大。
在每个 blk 前插入 PEG 效果更好。
对比实验 2:PEG 模块插入位置比较
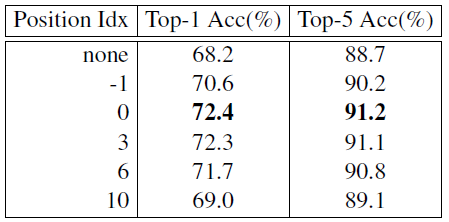
结论:
PEG 最佳的插入位置是第 1 个 encoder block 的输出到第 4 个 encoder block 的输出。
为什么插入位置为 - 1 (第 1 个 encoder block 的输入) 时的效果比插入位置为 0 时 (第 1 个 encoder block 的输出) 的效果差很多?
作者认为是插入位置为 - 1 的感受野更小,插入位置为 0 时的感受野更大。所以在插入位置为 - 1 时扩大感受野应该可以得到相似的性能。所以作者进行了下图 26 的实验:

把 3×3 卷积扩大为 27×27,并使用 13 的 zero-padding,扩大感受野后,在插入位置为 - 1 时得到了与插入位置为 0 时相似的性能。
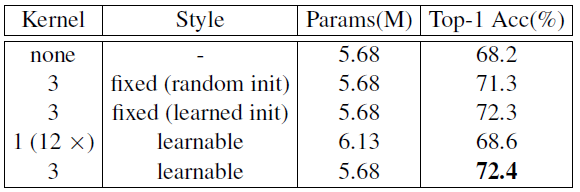
作者也在插入位置为 0 时使用了不同大小的卷积核:
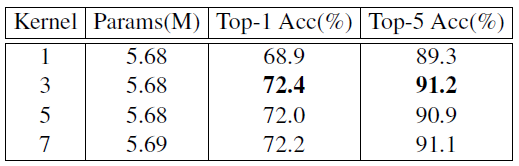
当卷积核为 1 时,由于无法获得位置信息,所以性能掉点严重,而卷积核为 5,7 时对性能提升意义不大。
作者进一步比较了在多个位置插入 PEG 模块给 Transformer 模型带来的影响,如下图 28 所示。
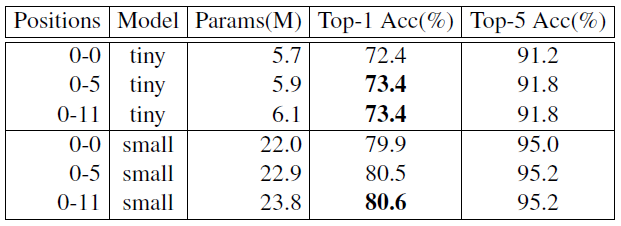
在 Tiny 模型的位置 0-5 都插入 PEG 模块时,性能超过了 DeiT-tiny 1.2%。插入过多的 PEG 模块的影响不大。
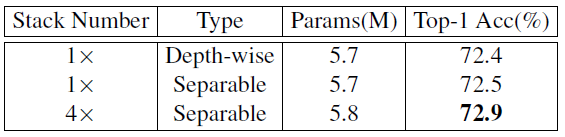
作者进一步对比了在 0 位置 PEG 使用 1 个 Depth-wise Convolution,1 个 Separable Convolution,4 个 Separable Convolution 的性能对比,如下图 29 所示。
使用 4 个 Separable Convolution 可以在只增加 0.1M 参数量的前提下获得 0.5% 的涨点。
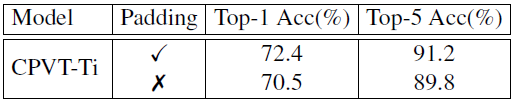
对比实验 3:Padding 的作用
为了探索 zero-padding 的作用,作者将它去掉之后再看 CPVT 模型的性能,降为了 70.5%。原因是 zero-padding 起到定位绝对位置的作用。它能暗示出图像的哪些部分是中间,哪些部分是边缘。这个实验也侧面证明了绝对位置编码的作用。
对比实验 4:到底是什么提升了性能?
作者想要探索到底是 PEG 的什么提升了性能,究竟是 PEG 卷积层的 representative power 还是它的位置表示能力?
- 如果是 PEG 卷积的位置表示能力起了作用,那我把卷积换成 FC 层,应该会掉点;
- 如果是 PEG 卷积的 representative power 起了作用,那我让卷积的参数固定住不更新,应该会掉点;
实验结果如图 30 所示,验证了第 1 点,所以是 PEG 卷积的位置表示能力在起作用。即使只使用卷积层而不学习它,那么通过 zero-padding 也可以把位置信息融入 Transformer 里面。
- 13.2 CVPT 代码解读:
Vision Transformer:
import torch
import torch.nn as nn
class VisionTransformer:
def __init__(layers=12, dim=192, nhead=3, img_size=224, patch_size=16):
self.pos_block = PEG(dim)
self.blocks = nn.ModuleList([TransformerEncoderLayer(dim, nhead, dim*4) for _ in range(layers)])
self.patch_embed = PatchEmbed(img_size, patch_size, dim*4)
def forward_features(self, x):
B, C, H, W = x.shape
x, patch_size = self.patch_embed(x)
_H, _W = H // patch_size, W // patch_size
# x: (b, N, d)
x = torch.cat((self.cls_tokens, x), dim=1)
# 循环通过所有的Encoder Blocks, 只是第1个encoder block的输出通过PEG模块.
for i, blk in enumerate(self.blocks):
x = blk(x)
# 第1个encoder block的输出通过PEG模块.
if i == 0:
x = self.pos_block(x, _H, _W)
return x[:, 0]
分类任务:PEG 模块:
class PEG(nn.Module):
def __init__(self, dim=256, k=3):
self.proj = nn.Conv2d(dim, dim, k, 1, k//2, groups=dim) # Only for demo use, more complicated functions are effective too.
def forward(self, x, H, W):
B, N, C = x.shape
# 把class token提出来, 不变.
# 只处理feat_token.
cls_token, feat_token = x[:, 0], x[:, 1:]
cnn_feat = feat_token.transpose(1, 2).view(B, C, H, W)
x = self.proj(cnn_feat) + cnn_feat
x = x.flatten(2).transpose(1, 2)
x = torch.cat((cls_token.unsqueeze(1), x), dim=1)
return x
检测任务:PEG 模块:
from torch import nn
class PEGDetection(nn.Module):
def __init__(self, in_chans):
super(PEGDetection, self).__init__()
self.proj = nn.Sequential(nn.Conv2d(in_chans, in_chans, 3, 1, 1, bias=False, groups=in_chans), nn.BatchNorm2d(in_chans), nn.ReLU())
def forward(self, x, mask, H, W):
"""
x N, B, C ; mask B N
"""
_, B, C = x.shape
_tmp = x.transpose(0, 1)[mask]
x = x.permute(1, 2, 0).view(B, C, H, W)
# 与分类任务不同,直接把x通过卷积之后与自己相加.
x = x + self.proj(cnn_feat)
x = x.flatten(2).transpose(1, 2)
# mask保持不变.
x[mask] = _tmp
return x.transpose(0, 1)
总结:¶
Patch 内部信息的处理与位置编码是 vision Transformer 的 2 个很重要的问题。本文深入探究了 2 种 vision Transformer 的内部机制,即:1. 如何更好地利用图像 patch 内部信息?2. 如何设计更灵活的位置编码?TNT 通过将 Patch 内部信息与 Patch 之间的信息融合,提升了 DeiT/ViT 的性能。CPVT 通过 PEG 模块代替传统的位置编码,实现了灵活的位置表示和更高效的位置信息编码,提升了 DeiT/ViT 的性能。值得一提的是,这 2 种方法与其他的改进措施是正交的,可以在不相互影响的条件下直接完成迁移。