Vision Transformer (一)
Attention
原文地址:https://zhuanlan.zhihu.com/p/340149804
目录¶
Transformer 是 Google 的团队在 2017 年提出的一种 NLP 经典模型,现在比较火热的 Bert 也是基于 Transformer。Transformer 模型使用了 Self-Attention 机制,不采用 RNN 的顺序结构,使得模型可以并行化训练,而且能够拥有全局信息。
1 一切从 Self-attention 开始¶
- 1.1 处理 Sequence 数据的模型:
Transformer 是一个 Sequence to Sequence model,特别之处在于它大量用到了 self-attention。
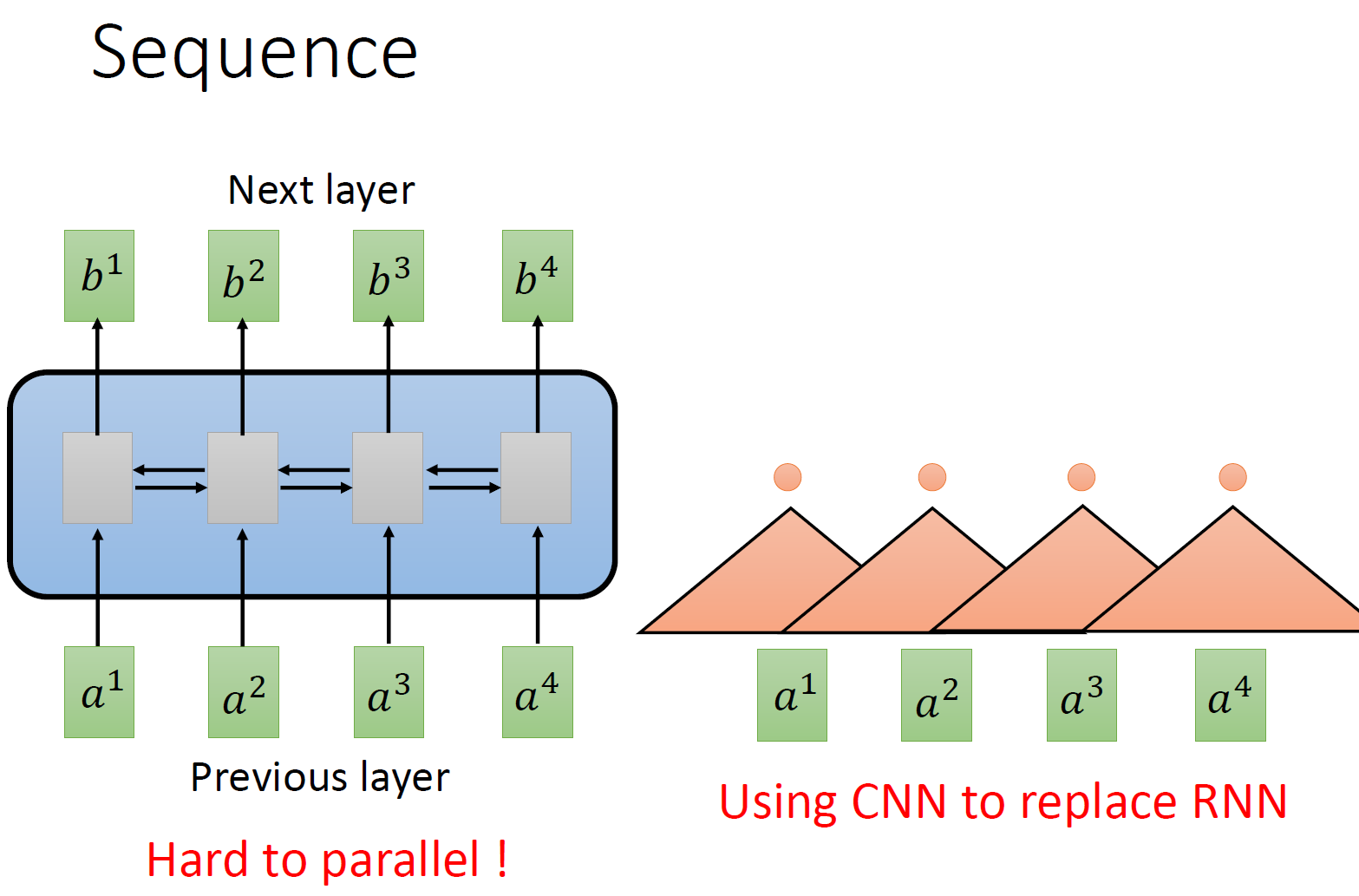
要处理一个 Sequence,最常想到的就是使用 RNN,它的输入是一串 vector sequence,输出是另一串 vector sequence,如下图 1 左所示。
如果假设是一个 single directional 的 RNN,那当输出 \(b_4\) 时,默认 \(a_1,a_2,a_3,a_4\) 都已经看过了。如果假设是一个 bi-directional 的 RNN,那当输出 \(b_{任意}\) 时,默认 \(a_1,a_2,a_3,a_4\) 都已经看过了。RNN 非常擅长于处理 input 是一个 sequence 的状况。
那 RNN 有什么样的问题呢?它的问题就在于:RNN 很不容易并行化 (hard to parallel)。
为什么说 RNN 很不容易并行化呢?假设在 single directional 的 RNN 的情形下,你今天要算出 \(b_4\) ,就必须要先看 \(a_1\) 再看 \(a_2\) 再看 \(a_3\) 再看 \(a_4\) ,所以这个过程很难平行处理。
所以今天就有人提出把 CNN 拿来取代 RNN,如下图 1 右所示。其中,橘色的三角形表示一个 filter,每次扫过 3 个向量 \(a\) ,扫过一轮以后,就输出了一排结果,使用橘色的小圆点表示。
这是第一个橘色的 filter 的过程,还有其他的 filter,比如图 2 中的黄色的 filter,它经历着与橘色的 filter 相似的过程,又输出一排结果,使用黄色的小圆点表示。
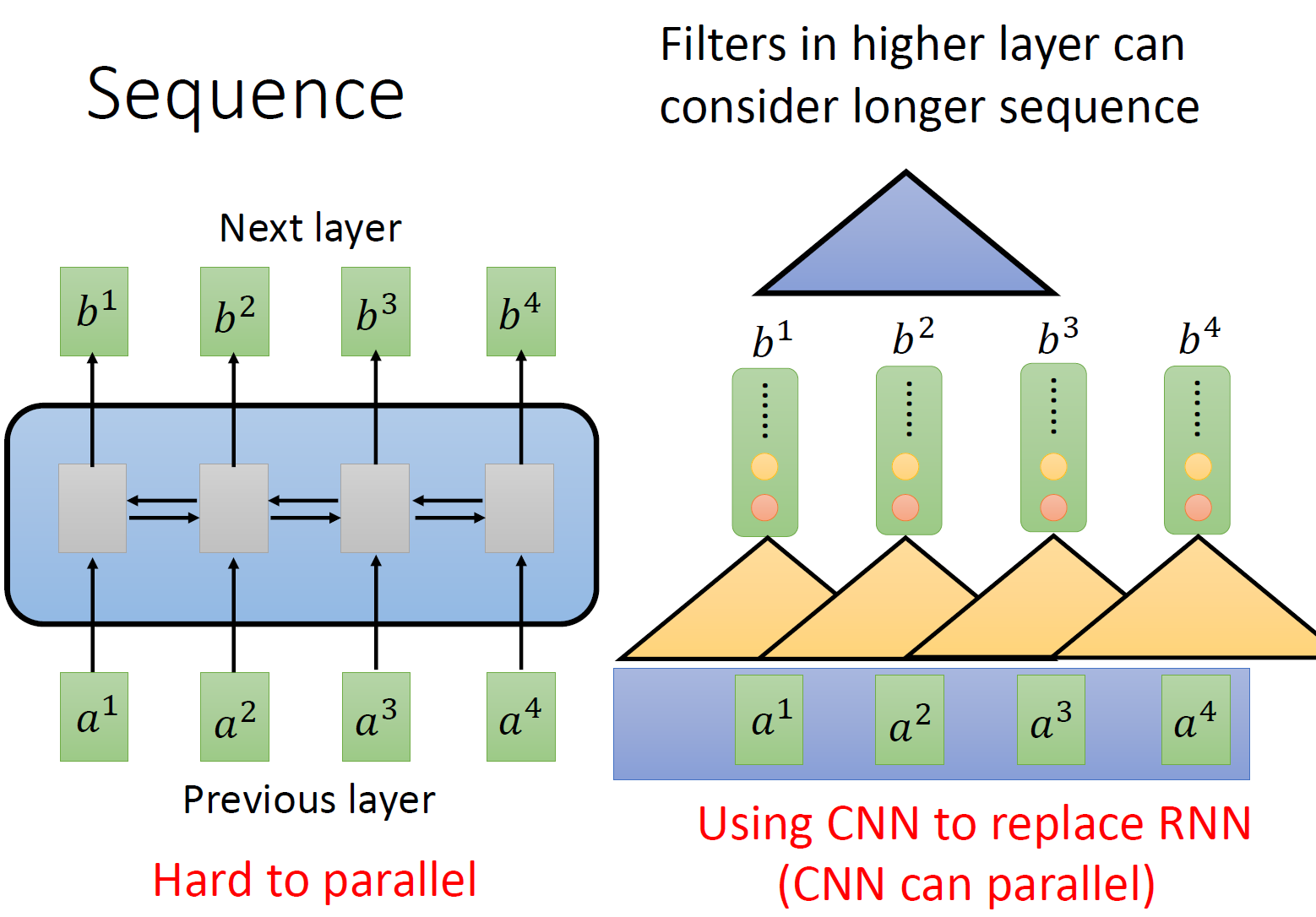
所以,用 CNN,你确实也可以做到跟 RNN 的输入输出类似的关系,也可以做到输入是一个 sequence,输出是另外一个 sequence。
但是,表面上 CNN 和 RNN 可以做到相同的输入和输出,但是 CNN 只能考虑非常有限的内容。比如在我们右侧的图中 CNN 的 filter 只考虑了 3 个 vector,不像 RNN 可以考虑之前的所有 vector。但是 CNN 也不是没有办法考虑很长时间的 dependency 的,你只需要堆叠 filter,多堆叠几层,上层的 filter 就可以考虑比较多的资讯,比如,第二层的 filter (蓝色的三角形) 看了 6 个 vector,所以,只要叠很多层,就能够看很长时间的资讯。
而 CNN 的一个好处是:它是可以并行化的 (can parallel),不需要等待红色的 filter 算完,再算黄色的 filter。但是必须要叠很多层 filter,才可以看到长时的资讯。所以今天有一个想法:self-attention,如下图 3 所示,目的是使用 self-attention layer 取代 RNN 所做的事情。
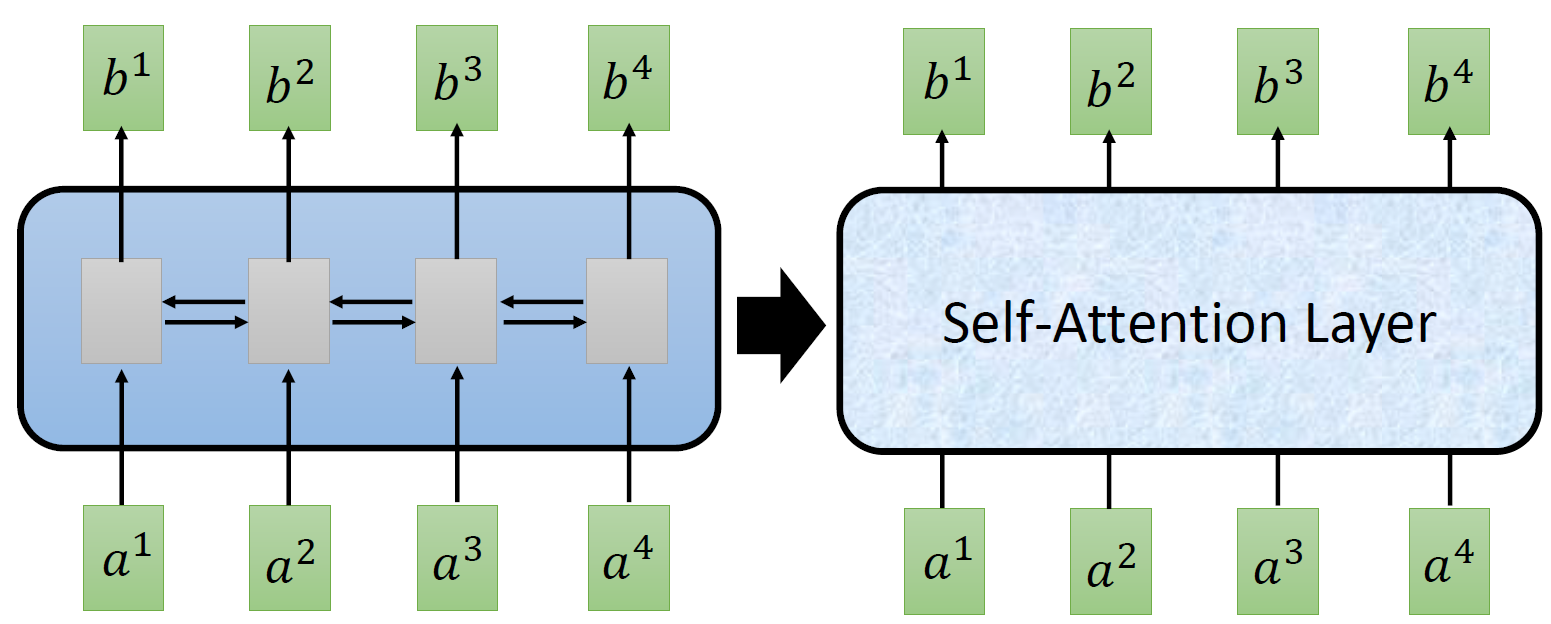
所以重点是:我们有一种新的 layer,叫 self-attention,它的输入和输出和 RNN 是一模一样的,输入一个 sequence,输出一个 sequence,它的每一个输出 \(b_1-b_4\) 都看过了整个的输入 sequence,这一点与 bi-directional RNN 相同。但是神奇的地方是:它的每一个输出 \(b_1-b_4\) 可以并行化计算。
- 1.2 Self-attention:
那么 self-attention 具体是怎么做的呢?
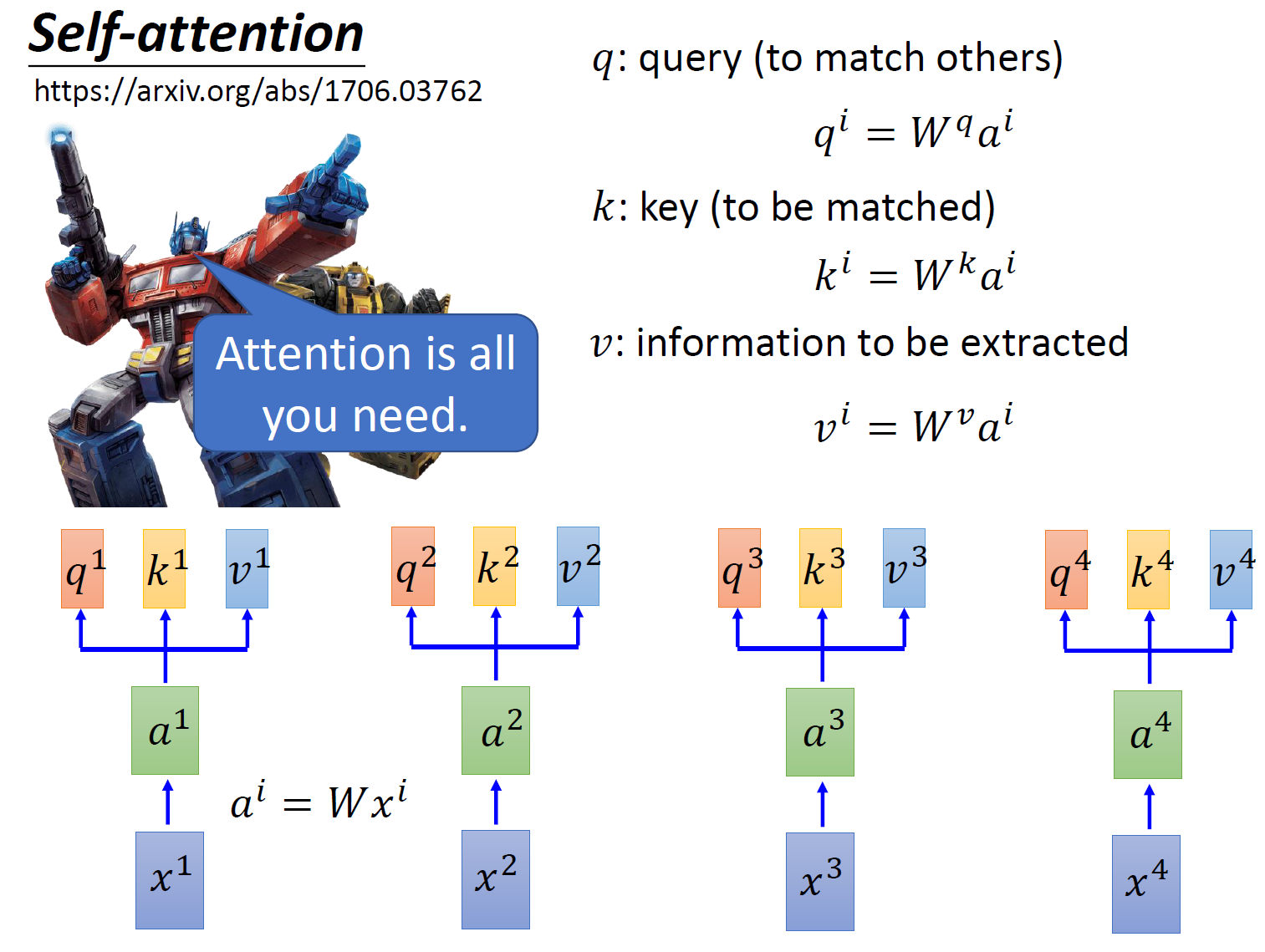
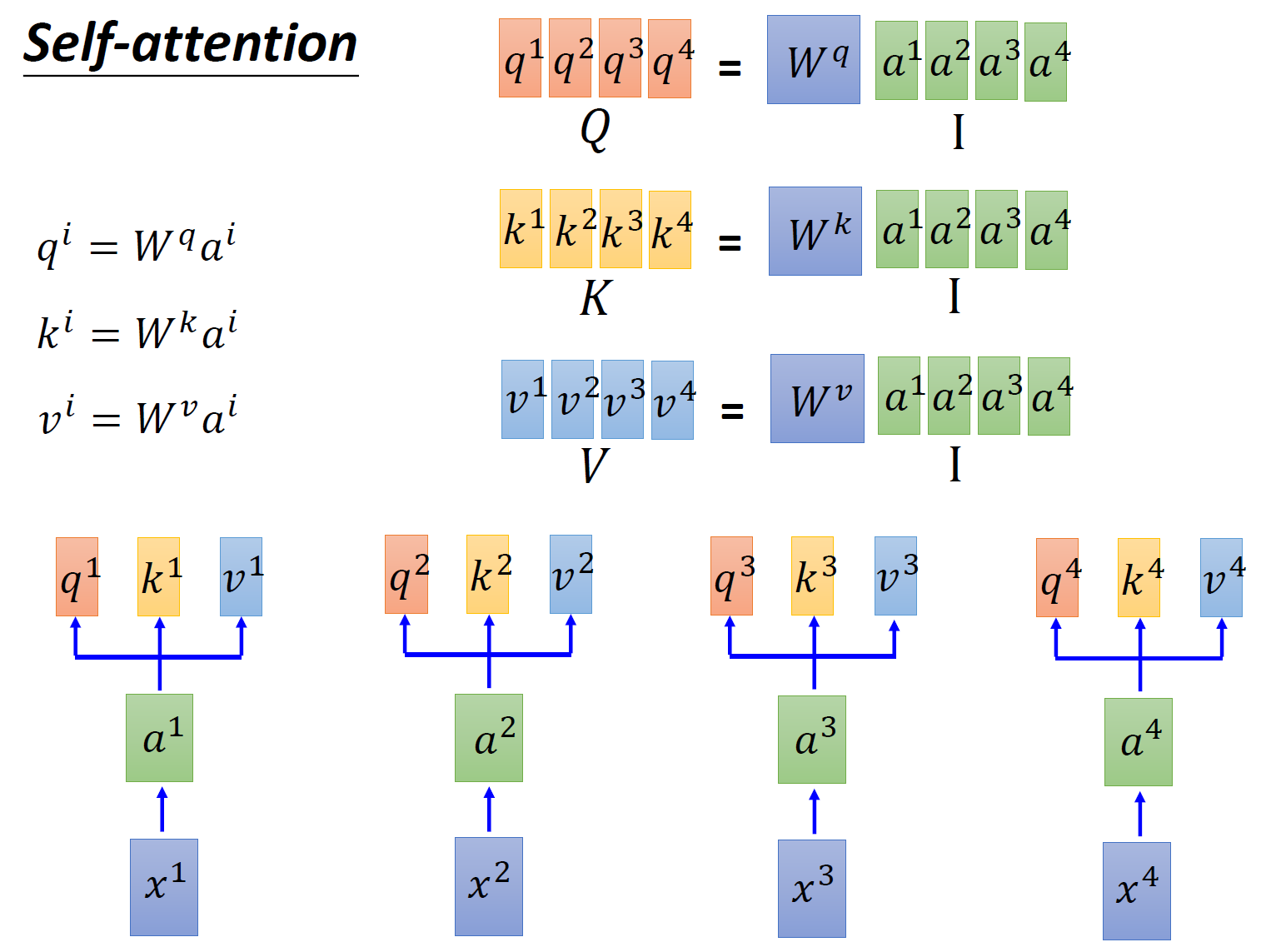
首先假设我们的 input 是图 4 的 \(x_1-x_4\) ,是一个 sequence,每一个 input (vector) 先乘上一个矩阵 \(W\) 得到 embedding,即向量 \(a_1-a_4\) 。接着这个 embedding 进入 self-attention 层,每一个向量 \(a_1-a_4\) 分别乘上 3 个不同的 transformation matrix \(W_q,W_k,W_v\) ,以向量 \(a_1\) 为例,分别得到 3 个不同的向量 \(q_1,k_1,v_1\) 。
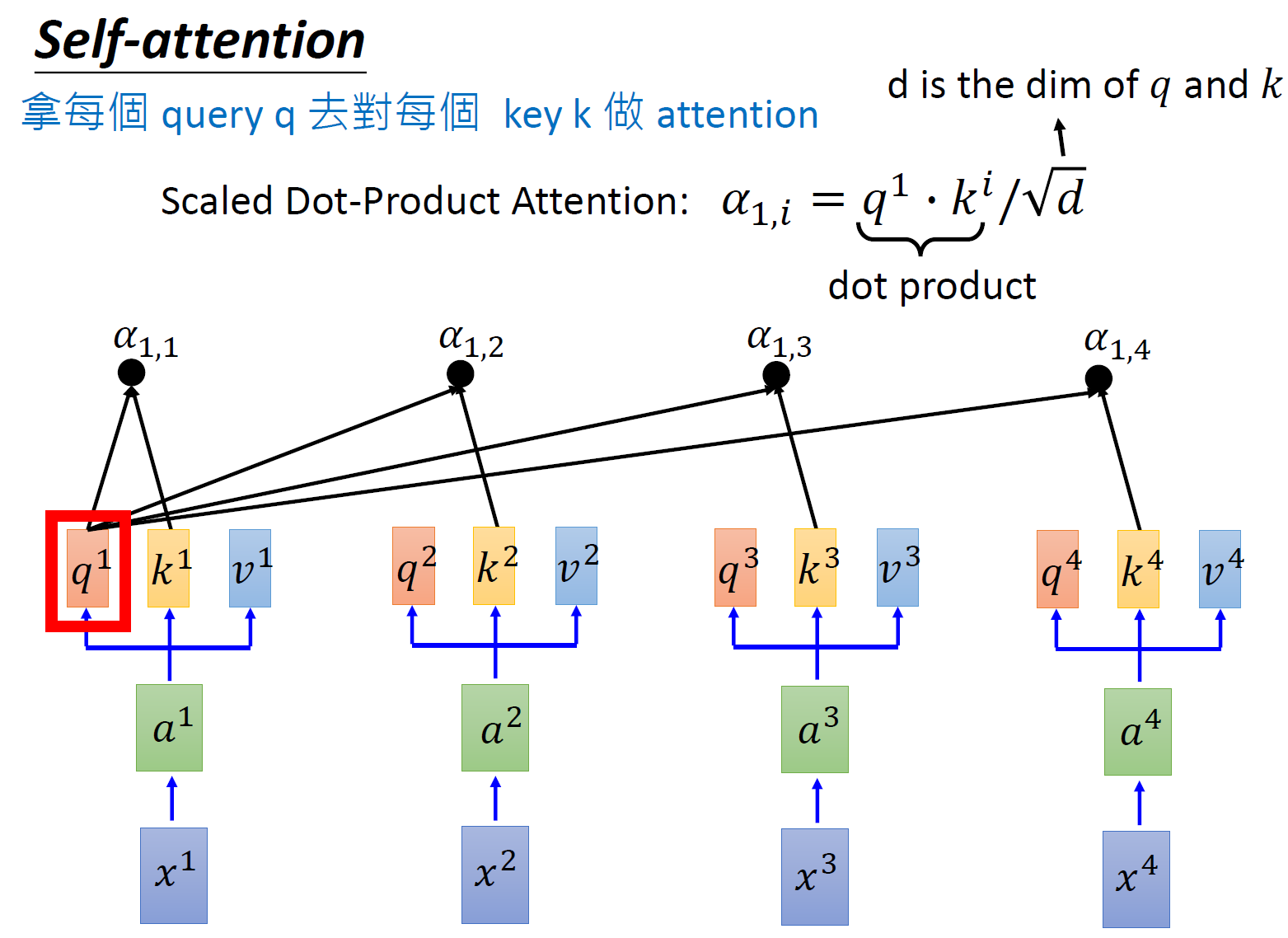
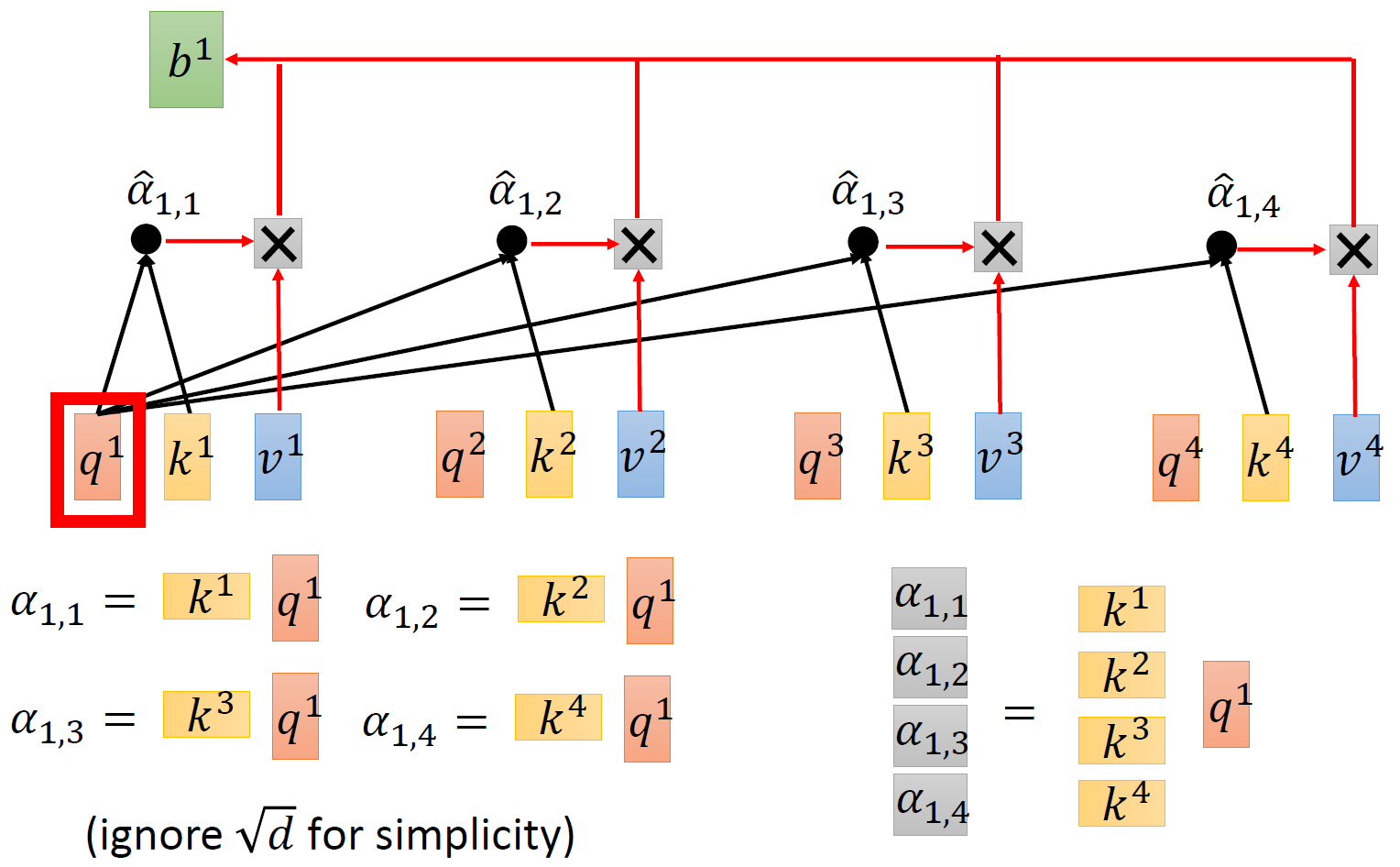
接下来使用每个 query \(q\) 去对每个 key \(k\) 做 attention,attention 就是匹配这 2 个向量有多接近,比如我现在要对 \(q^1\) 和 \(k^1\) 做 attention,我就可以把这 2 个向量做 scaled inner product,得到 \(\alpha_{1,1}\) 。接下来你再拿 \(q^1\) 和 \(k^2\) 做 attention,得到 \(\alpha_{1,2}\) ,你再拿 \(q^1\) 和 \(k^3\) 做 attention,得到 \(\alpha_{1,3}\) ,你再拿 \(q^1\) 和 \(k^4\) 做 attention,得到 \(\alpha_{1,4}\) 。那这个 scaled inner product 具体是怎么计算的呢?
式中, \(d\) 是 \(q\) 跟 \(k\) 的维度。因为 \(q\cdot k\) 的数值会随着 dimension 的增大而增大,所以要除以 \(\sqrt{\text{dimension}}\) 的值,相当于归一化的效果。
接下来要做的事如图 6 所示,把计算得到的所有 \(\alpha_{1,i}\) 值取 \(\text{softmax}\) 操作。
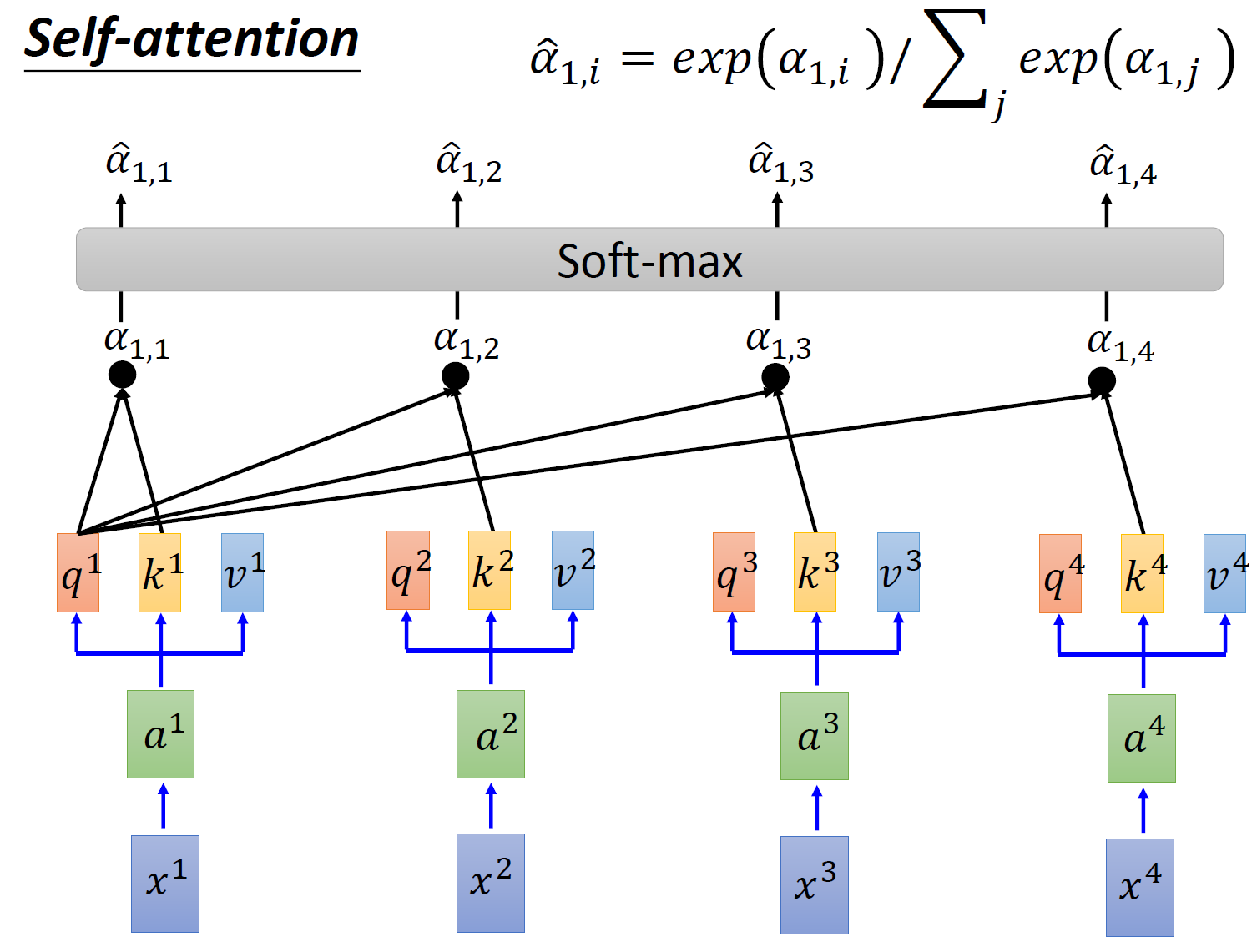
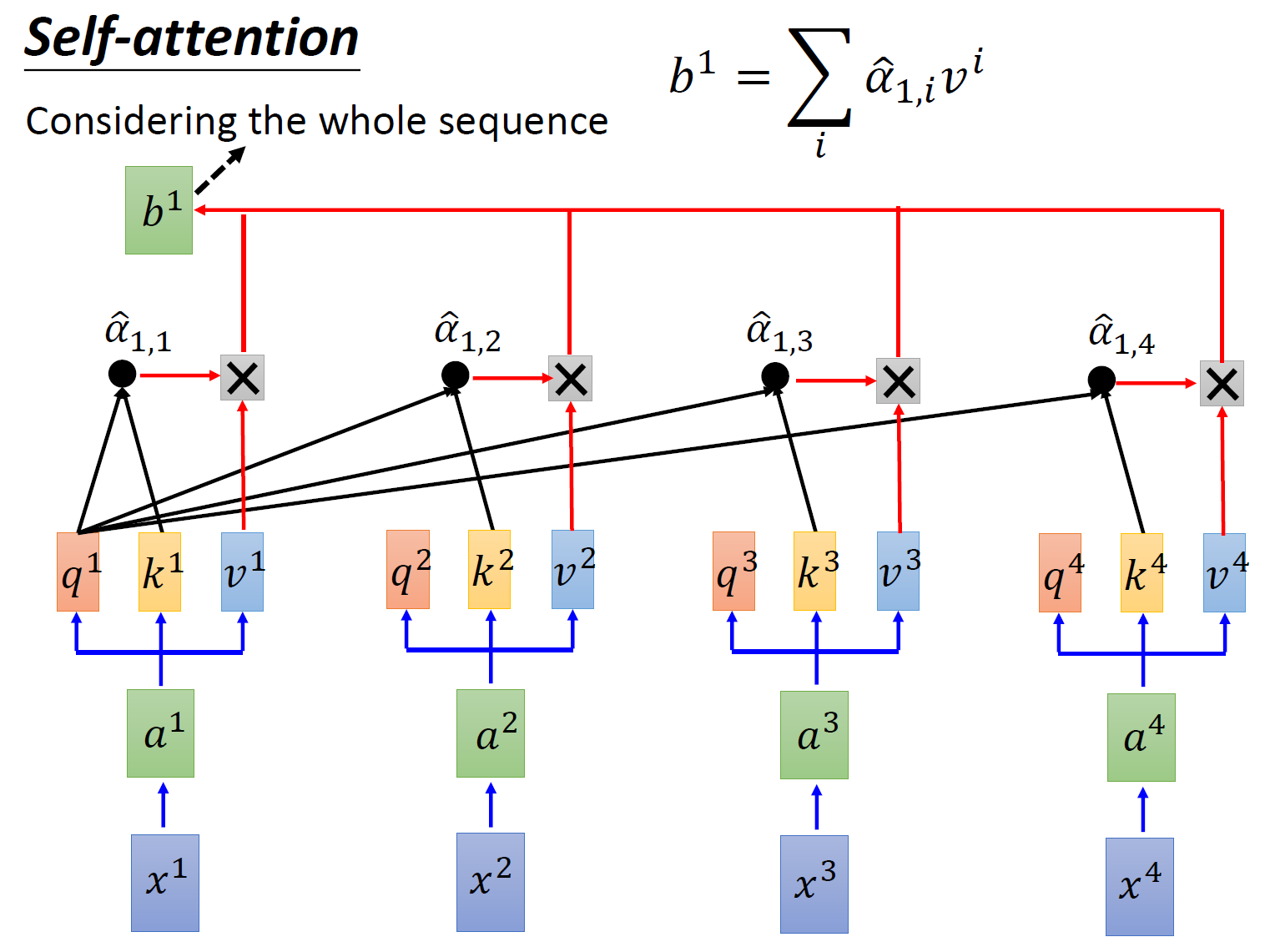
取完 \(\text{softmax}\) 操作以后,我们得到了 \(\hat \alpha_{1,i}\) ,我们用它和所有的 \(v^i\) 值进行相乘。具体来讲,把 \(\hat \alpha_{1,1}\) 乘上 \(v^1\) ,把 \(\hat \alpha_{1,2}\) 乘上 \(v^2\) ,把 \(\hat \alpha_{1,3}\) 乘上 \(v^3\) ,把 \(\hat \alpha_{1,4}\) 乘上 \(v^4\) ,把结果通通加起来得到 \(b^1\) ,所以,今天在产生 \(b^1\) 的过程中用了整个 sequence 的资讯 (Considering the whole sequence)。如果要考虑 local 的 information,则只需要学习出相应的 \(\hat \alpha_{1,i}=0\) , \(b^1\) 就不再带有那个对应分支的信息了;如果要考虑 global 的 information,则只需要学习出相应的 \(\hat \alpha_{1,i}\ne0\) , \(b^1\) 就带有全部的对应分支的信息了。
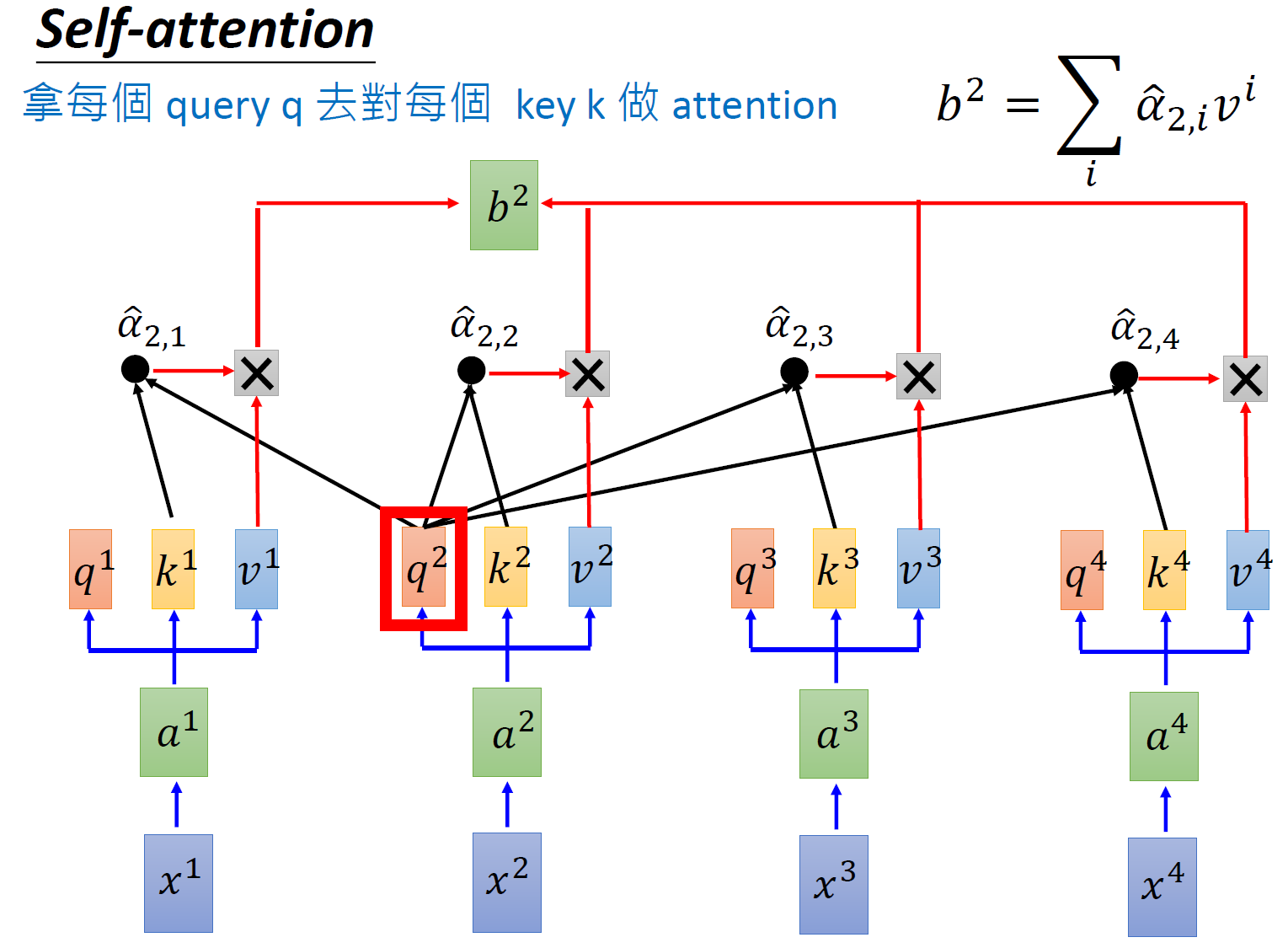
同样的方法,也可以计算出 \(b^2,b^3,b^4\) ,如下图 8 所示, \(b^2\) 就是拿 query \(q^2\) 去对其他的 \(k\) 做 attention,得到 \(\hat \alpha_{2,i}\) ,再与 value 值 \(v^i\) 相乘取 weighted sum 得到的。
经过了以上一连串计算,self-attention layer 做的事情跟 RNN 是一样的,只是它可以并行的得到 layer 输出的结果,如图 9 所示。现在我们要用矩阵表示上述的计算过程。
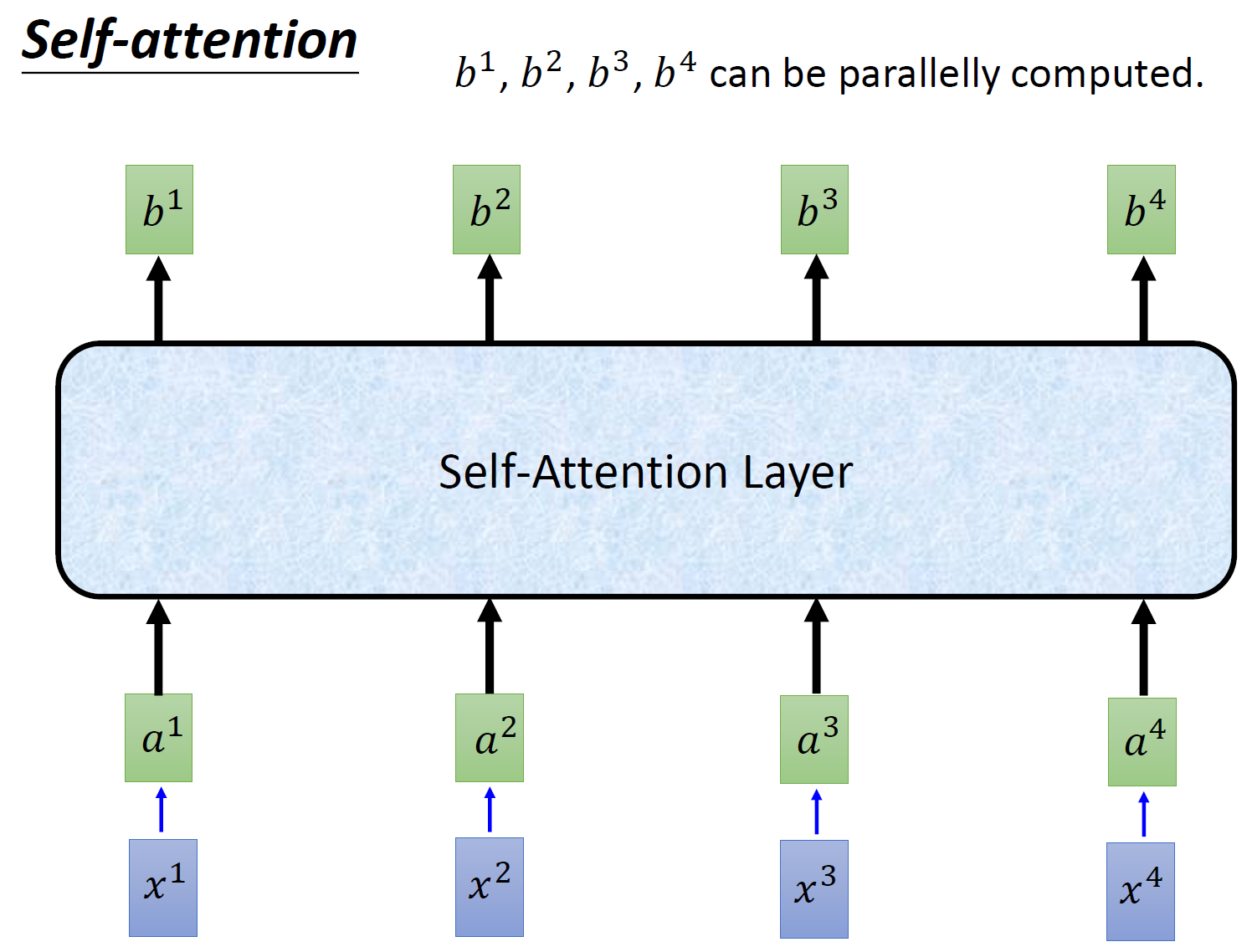
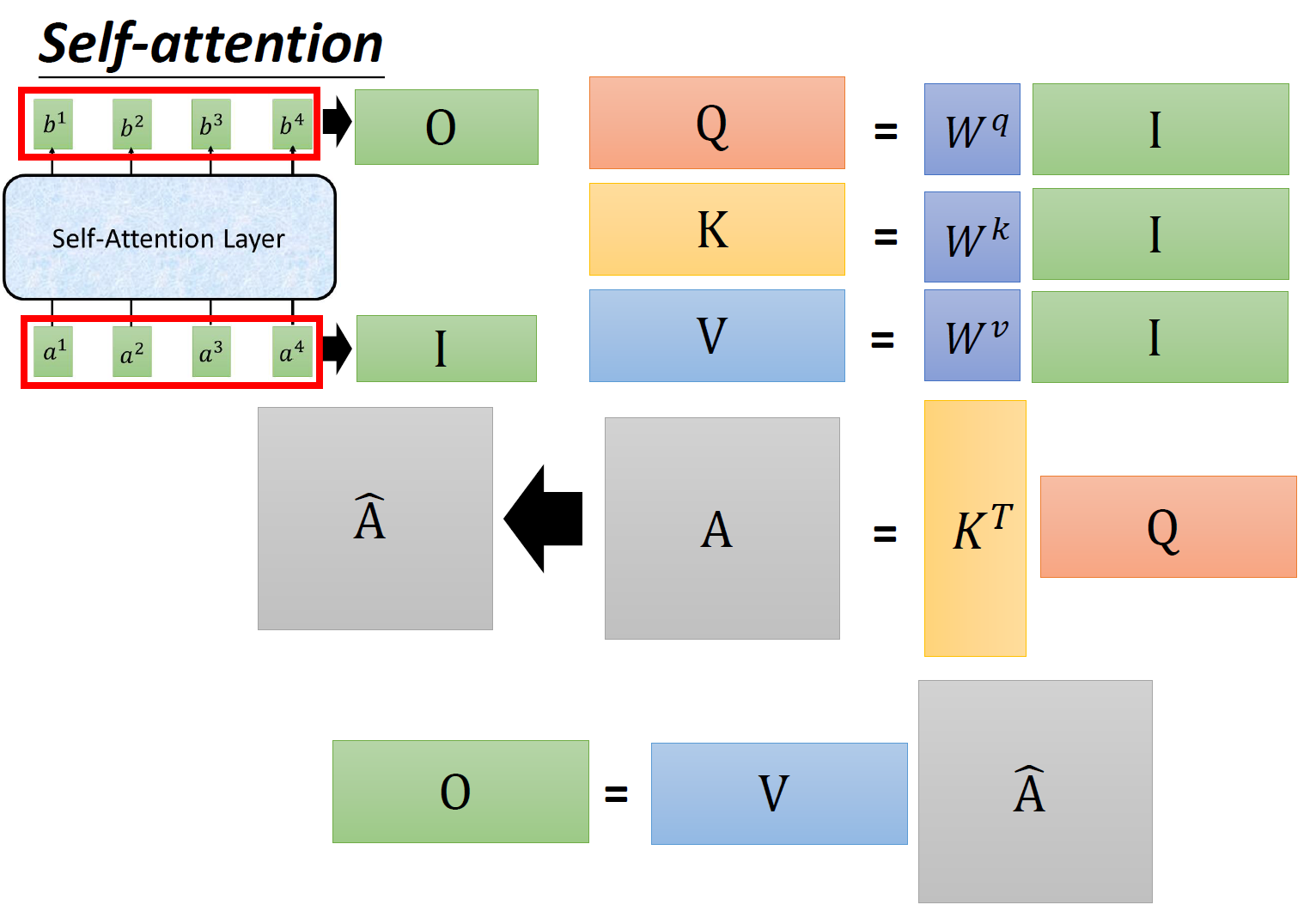
首先输入的 embedding 是 \(I=[a^1,a^2,a^3,a^4]\) ,然后用 \(I\) 乘以 transformation matrix \(W^q\) 得到 \(Q=[q^1,q^2,q^3,q^4]\) ,它的每一列代表着一个 vector \(q\) 。同理,用 \(I\) 乘以 transformation matrix \(W^k\) 得到 \(K=[k^1,k^2,k^3,k^4]\) ,它的每一列代表着一个 vector \(k\) 。用 \(I\) 乘以 transformation matrix \(W^v\) 得到 \(V=[v^1,v^2,v^3,v^4]\) ,它的每一列代表着一个 vector \(v\) 。
接下来是 \(k\) 与 \(q\) 的 attention 过程,我们可以把 vector \(k\) 横过来变成行向量,与列向量 \(q\) 做内积,这里省略了 \(\sqrt{d}\) 。这样, \(\alpha\) 就成为了 \(4\times4\) 的矩阵,它由 4 个行向量拼成的矩阵和 4 个列向量拼成的矩阵做内积得到,如图 11 所示。
在得到 \(\hat A\) 以后,如上文所述,要得到 \(b^1\), 就要使用 \(\hat \alpha_{1,i}\) 分别与 \(v^i\) 相乘再求和得到,所以 \(\hat A\) 要再左乘 \(V\) 矩阵。

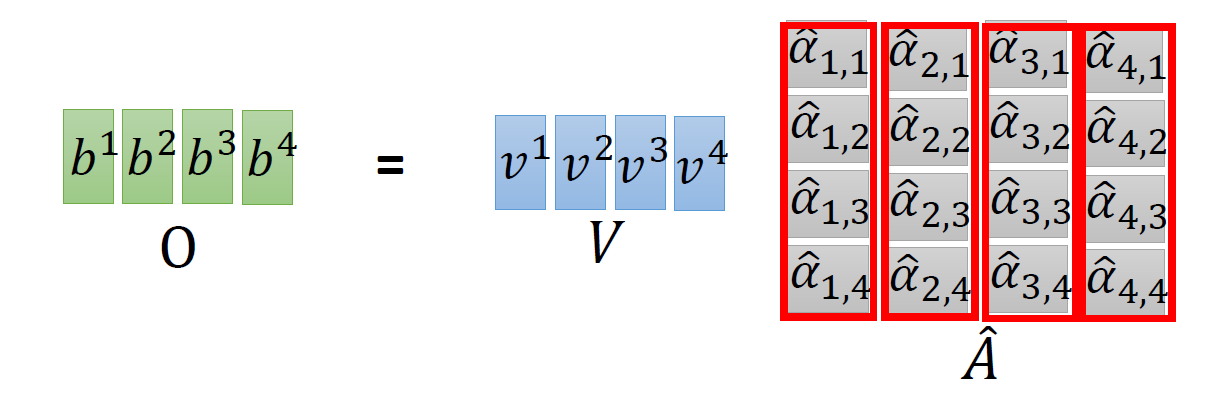
到这里你会发现这个过程可以被表示为,如图 12 所示:输入矩阵 \(I\in R (d,N)\) 分别乘上 3 个不同的矩阵 \(W_q,W_k,W_v \in R (d,d)\) 得到 3 个中间矩阵 \(Q,K,V\in R (d,N)\) 。它们的维度是相同的。把 \(K\) 转置之后与 \(Q\) 相乘得到 Attention 矩阵 \(A\in R (N,N)\) ,代表每一个位置两两之间的 attention。再将它取 \(\text{softmax}\) 操作得到 \(\hat A\in R (N,N)\) ,最后将它乘以 \(V\) 矩阵得到输出 vector \(O\in R (d,N)\) 。
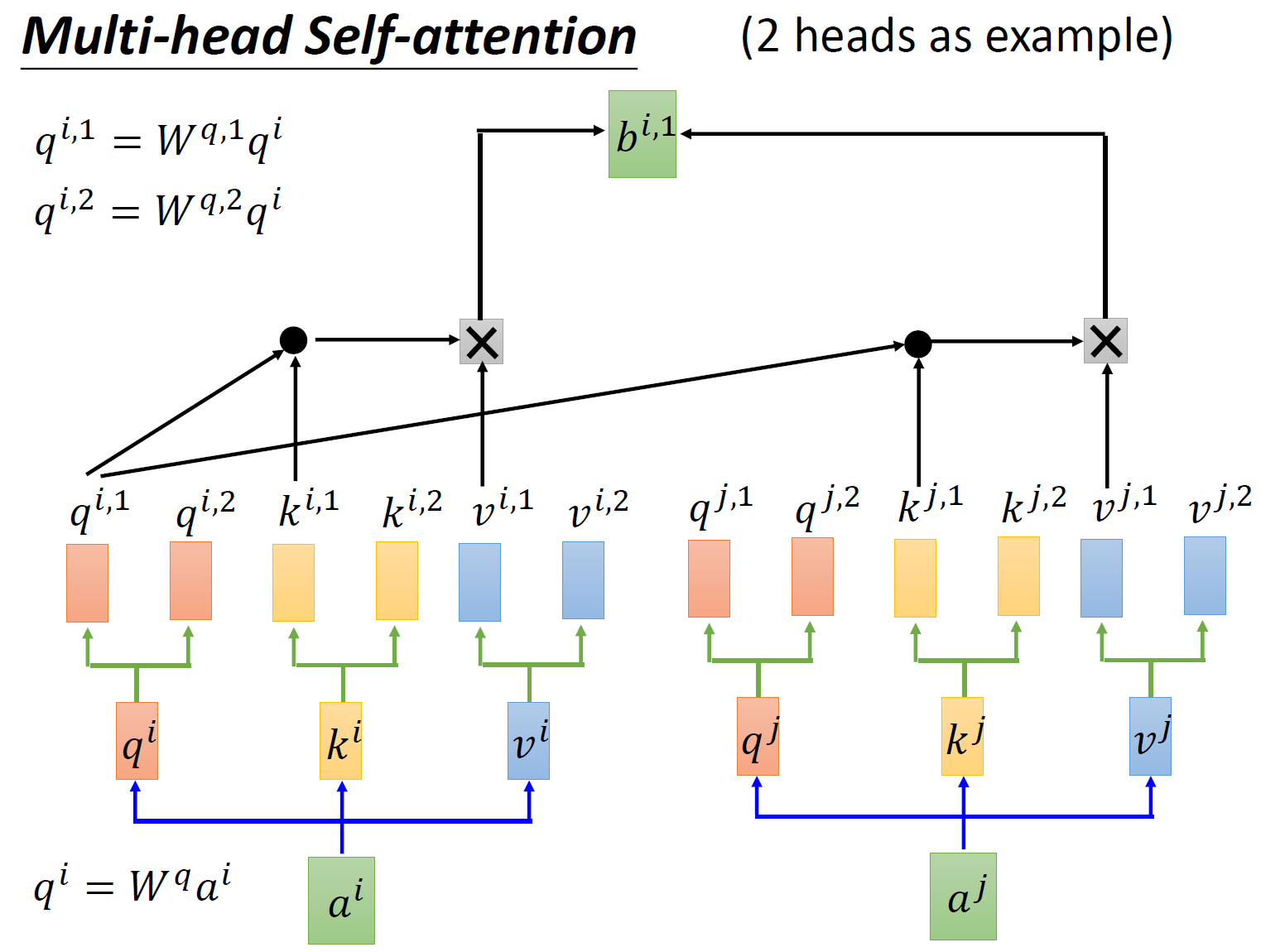
- 1.3 Multi-head Self-attention:
还有一种 multi-head 的 self-attention,以 2 个 head 的情况为例:由 \(a^i\) 生成的 \(q^i\) 进一步乘以 2 个转移矩阵变为 \(q^{i,1}\) 和 \(q^{i,2}\) ,同理由 \(a^i\) 生成的 \(k^i\) 进一步乘以 2 个转移矩阵变为 \(k^{i,1}\) 和 \(k^{i,2}\) ,由 \(a^i\) 生成的 \(v^i\) 进一步乘以 2 个转移矩阵变为 \(v^{i,1}\) 和 \(v^{i,2}\) 。接下来 \(q^{i,1}\) 再与 \(k^{i,1}\) 做 attention,得到 weighted sum 的权重 \(\alpha\) ,再与 \(v^{i,1}\) 做 weighted sum 得到最终的 \(b^{i,1}(i=1,2,...,N)\) 。同理得到 \(b^{i,2}(i=1,2,...,N)\) 。现在我们有了 \(b^{i,1}(i=1,2,...,N)\in R(d,1)\) 和 \(b^{i,2}(i=1,2,...,N)\in R(d,1)\) ,可以把它们 concat 起来,再通过一个 transformation matrix 调整维度,使之与刚才的 \(b^{i}(i=1,2,...,N)\in R(d,1)\) 维度一致 (这步如图 13 所示)。
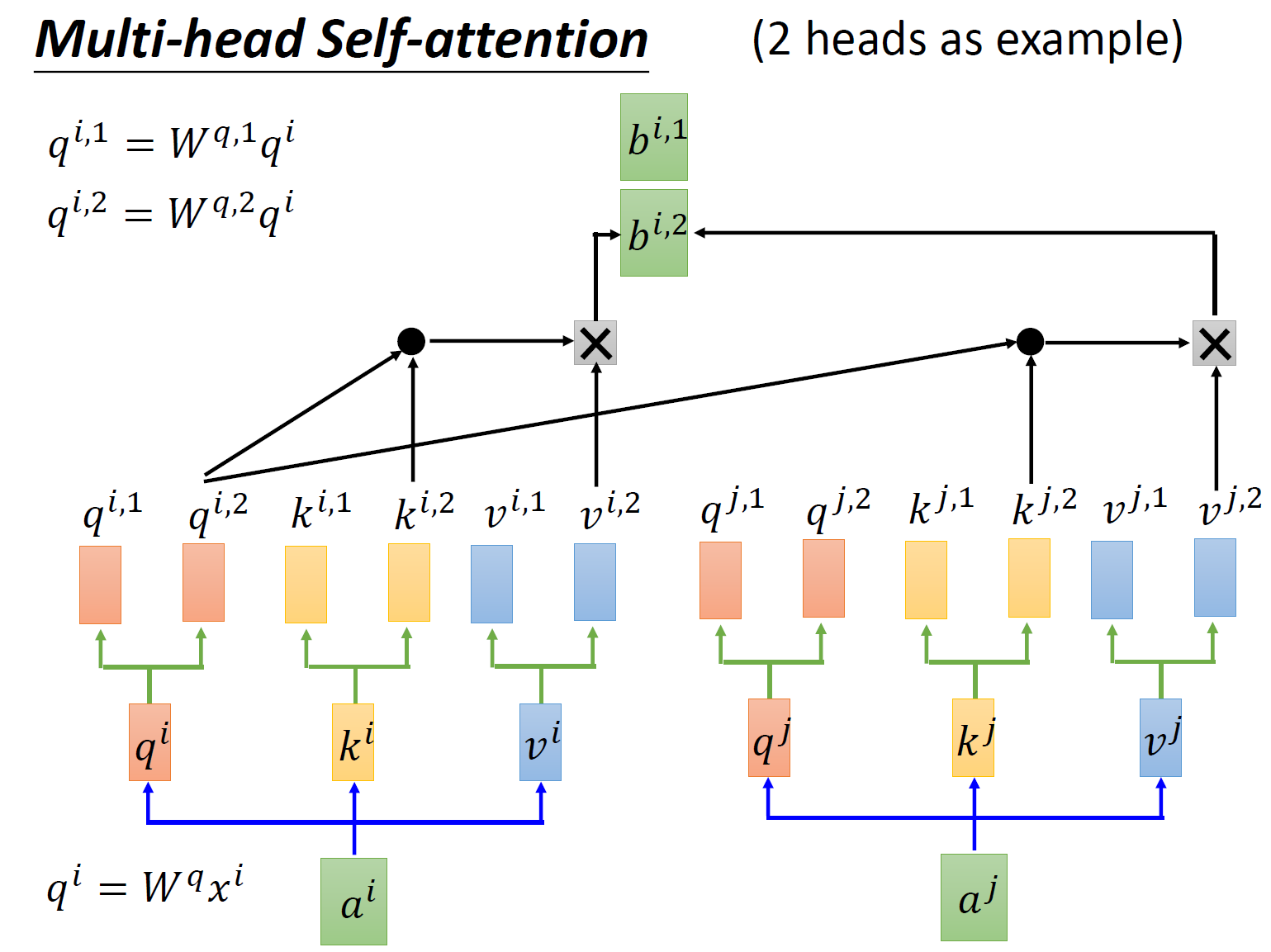
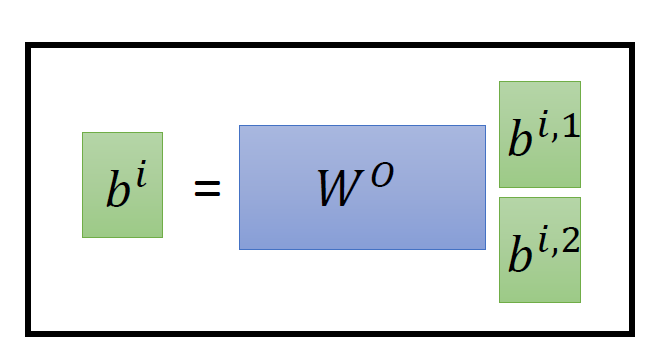
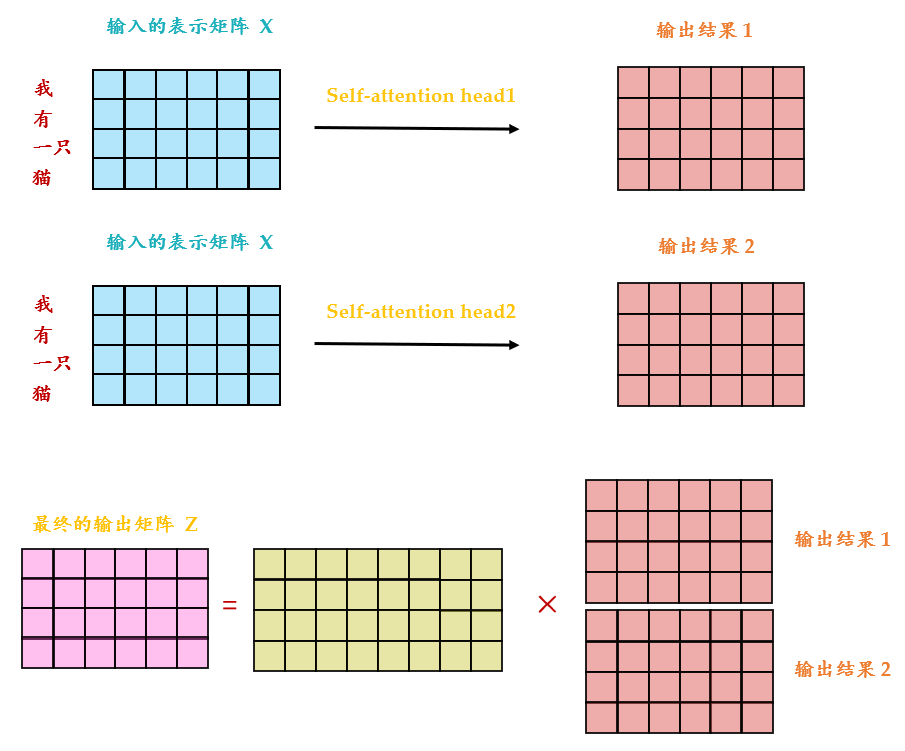
从下图 14 可以看到 Multi-Head Attention 包含多个 Self-Attention 层,首先将输入 \(X\) 分别传递到 2 个不同的 Self-Attention 中,计算得到 2 个输出结果。得到 2 个输出矩阵之后,Multi-Head Attention 将它们拼接在一起 (Concat),然后传入一个 Linear 层,得到 Multi-Head Attention 最终的输出 \(Z\) 。可以看到 Multi-Head Attention 输出的矩阵 \(Z\) 与其输入的矩阵 \(X\) 的维度是一样的。
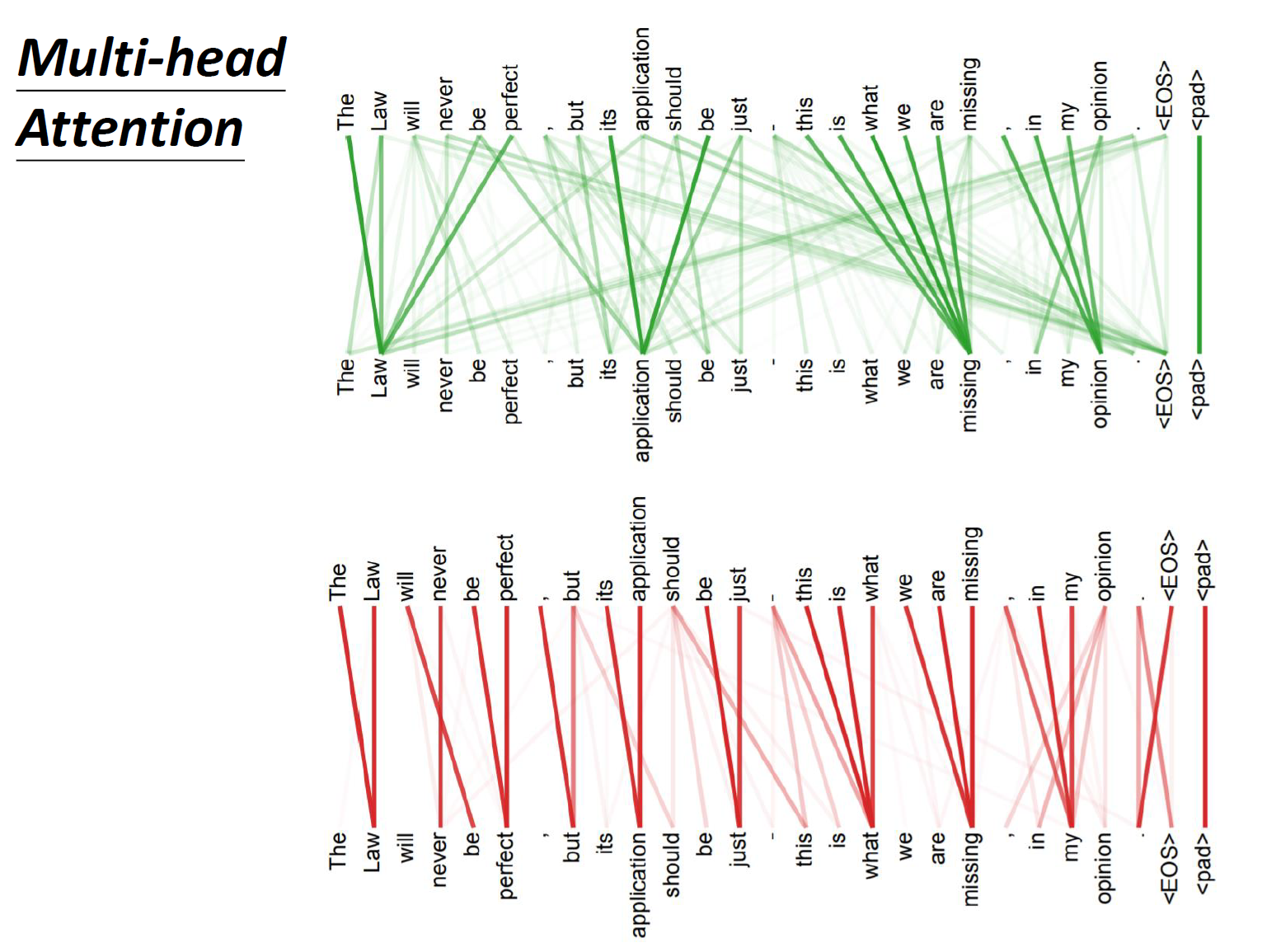
这里有一组 Multi-head Self-attention 的解果,其中绿色部分是一组 query 和 key,红色部分是另外一组 query 和 key,可以发现绿色部分其实更关注 global 的信息,而红色部分其实更关注 local 的信息。
- 1.4 Positional Encoding:
以上是 multi-head self-attention 的原理,但是还有一个问题是:现在的 self-attention 中没有位置的信息,一个单词向量的 “近在咫尺” 位置的单词向量和 “远在天涯” 位置的单词向量效果是一样的,没有表示位置的信息(No position information in self attention)。所以你输入 "A 打了 B" 或者 "B 打了 A" 的效果其实是一样的,因为并没有考虑位置的信息。所以在 self-attention 原来的 paper 中,作者为了解决这个问题所做的事情是如下图 16 所示:
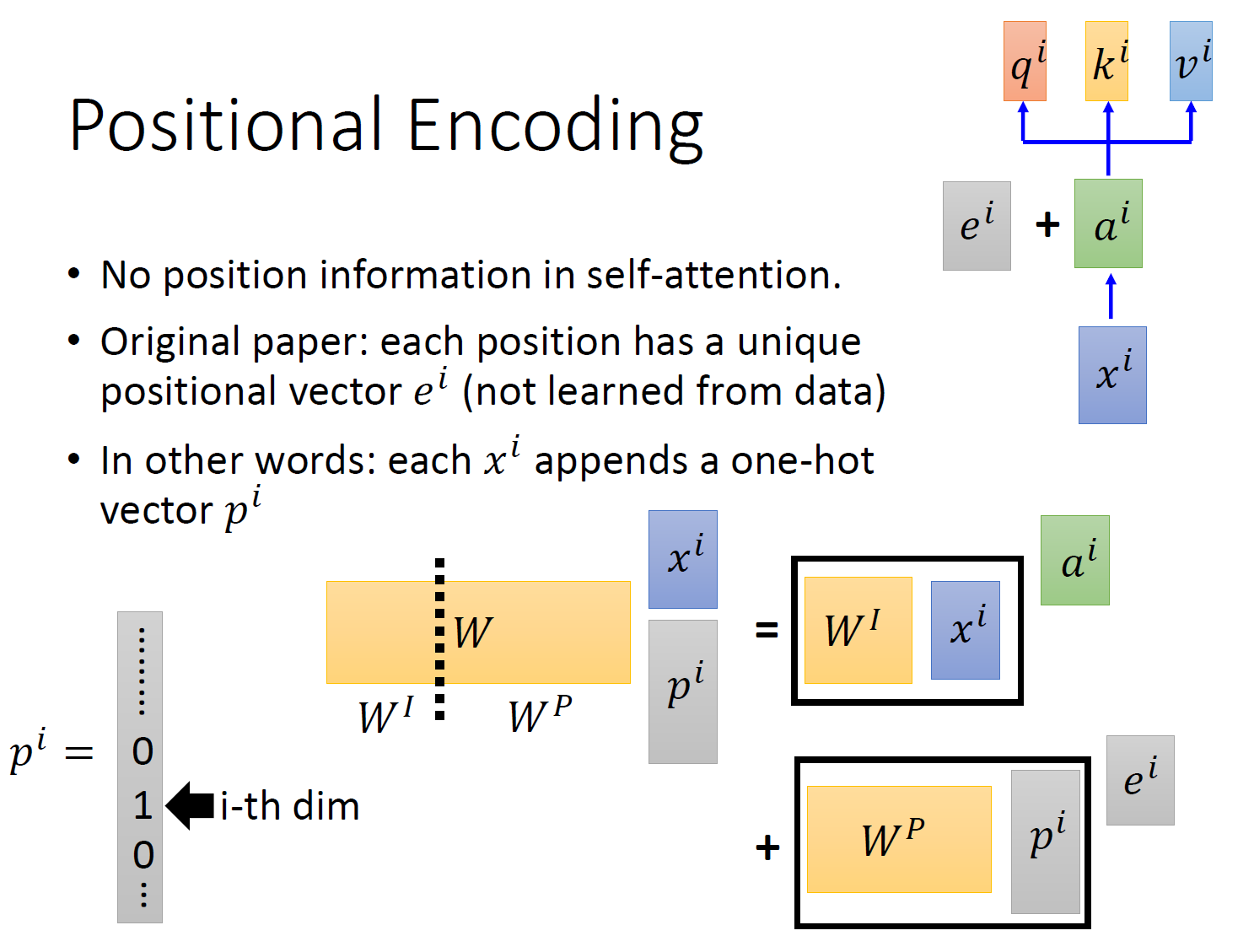
具体的做法是:给每一个位置规定一个表示位置信息的向量 \(e^i\) ,让它与 \(a^i\) 加在一起之后作为新的 \(a^i\) 参与后面的运算过程,但是这个向量 \(e^i\) 是由人工设定的,而不是神经网络学习出来的。每一个位置都有一个不同的 \(e^i\) 。
那到这里一个自然而然的问题是:为什么是 \(e^i\) 与 \(a^i\) 相加?为什么不是 concatenate?加起来以后,原来表示位置的资讯不就混到 \(a^i\) 里面去了吗?不就很难被找到了吗?
这里提供一种解答这个问题的思路:
如图 15 所示,我们先给每一个位置的 \(x^i\in R(d,1)\) append 一个 one-hot 编码的向量 \(p^i\in R(N,1)\) ,得到一个新的输入向量 \(x_p^i\in R(d+N,1)\) ,这个向量作为新的输入,乘以一个 transformation matrix \(W=[W^I,W^P]\in R(d,d+N)\) 。那么:
所以,\(e^i\) 与 \(a^i\) 相加就等同于把原来的输入 \(x^i\) concat 一个表示位置的独热编码 \(p^i\) ,再做 transformation。
这个与位置编码乘起来的矩阵 \(W^P\) 是手工设计的,如图 17 所示 (黑色框代表一个位置的编码)。
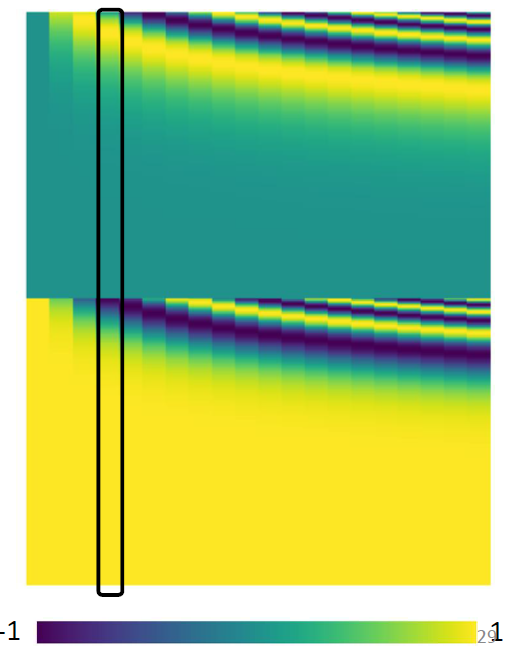
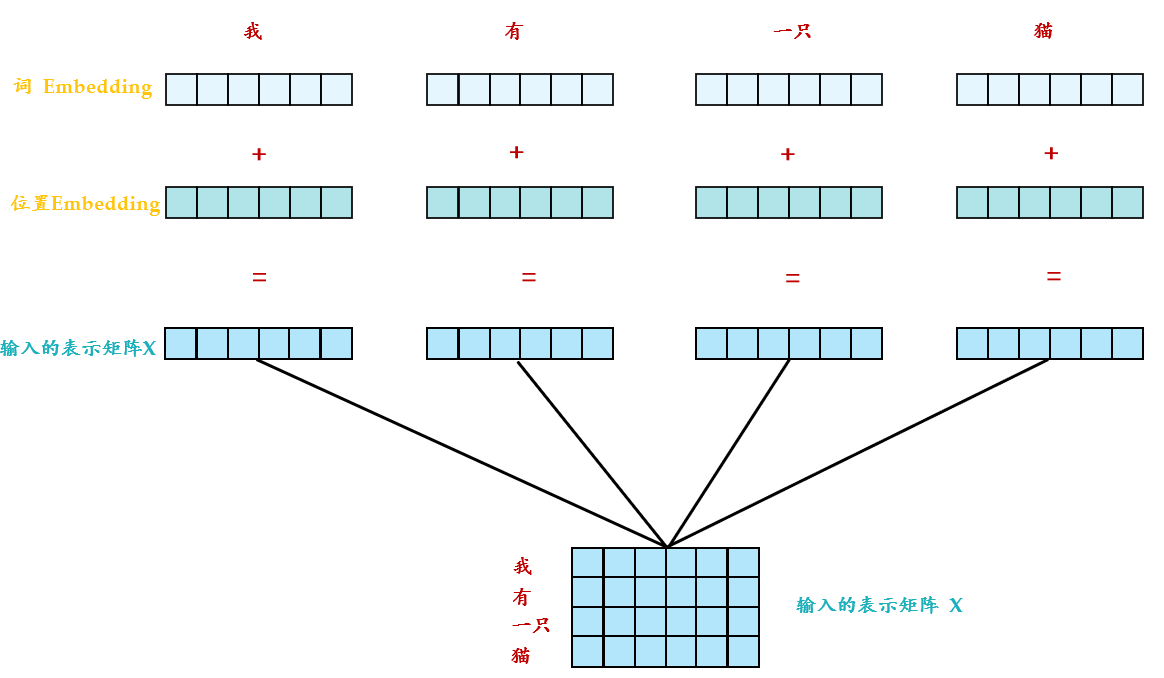
Transformer 中除了单词的 Embedding,还需要使用位置 Embedding 表示单词出现在句子中的位置。因为 Transformer 不采用 RNN 的结构,而是使用全局信息,不能利用单词的顺序信息,而这部分信息对于 NLP 来说非常重要。所以 Transformer 中使用位置 Embedding 保存单词在序列中的相对或绝对位置。
位置 Embedding 用 PE 表示,PE 的维度与单词 Embedding 是一样的。PE 可以通过训练得到,也可以使用某种公式计算得到。在 Transformer 中采用了后者,计算公式如下:
式中, \(pos\) 表示 token 在 sequence 中的位置,例如第一个 token "我" 的 \(pos=0\) 。
\(i\) ,或者准确意义上是 \(2i\) 和 \(2i+1\) 表示了 Positional Encoding 的维度,\(i\) 的取值范围是: \(\left[ 0,\ldots ,{{{d}_{model}}}/{2}\; \right)\) 。所以当 \(pos\) 为 1 时,对应的 Positional Encoding 可以写成:
\(PE\left( 1 \right)=\left[ \sin \left( {1}/{{{10000}^{{0}/{512}\;}}}\; \right),\cos \left( {1}/{{{10000}^{{0}/{512}\;}}}\; \right),\sin \left( {1}/{{{10000}^{{2}/{512}\;}}}\; \right),\cos \left( {1}/{{{10000}^{{2}/{512}\;}}}\; \right),\ldots \right]\)
式中, \({{d}_{model}}=512\)。底数是 10000。为什么要使用 10000 呢,这个就类似于玄学了,原论文中完全没有提啊,这里不得不说说论文的 readability 的问题,即便是很多高引的文章,最基本的内容都讨论不清楚,所以才出现像上面提问里的讨论,说实话这些论文还远远没有做到 easy to follow。这里我给出一个假想:\({{10000}^{{1}/{512}}}\) 是一个比较接近 1 的数(1.018),如果用 100000,则是 1.023。这里只是猜想一下,其实大家应该完全可以使用另一个底数。
这个式子的好处是:
- 每个位置有一个唯一的 positional encoding。
- 使 \(PE\) 能够适应比训练集里面所有句子更长的句子,假设训练集里面最长的句子是有 20 个单词,突然来了一个长度为 21 的句子,则使用公式计算的方法可以计算出第 21 位的 Embedding。
- 可以让模型容易地计算出相对位置,对于固定长度的间距 \(k\) ,任意位置的 \(PE_{pos+k}\) 都可以被 \(PE_{pos}\) 的线性函数表示,因为三角函数特性:
除了以上的固定位置编码以外,还有其他的很多表示方法:
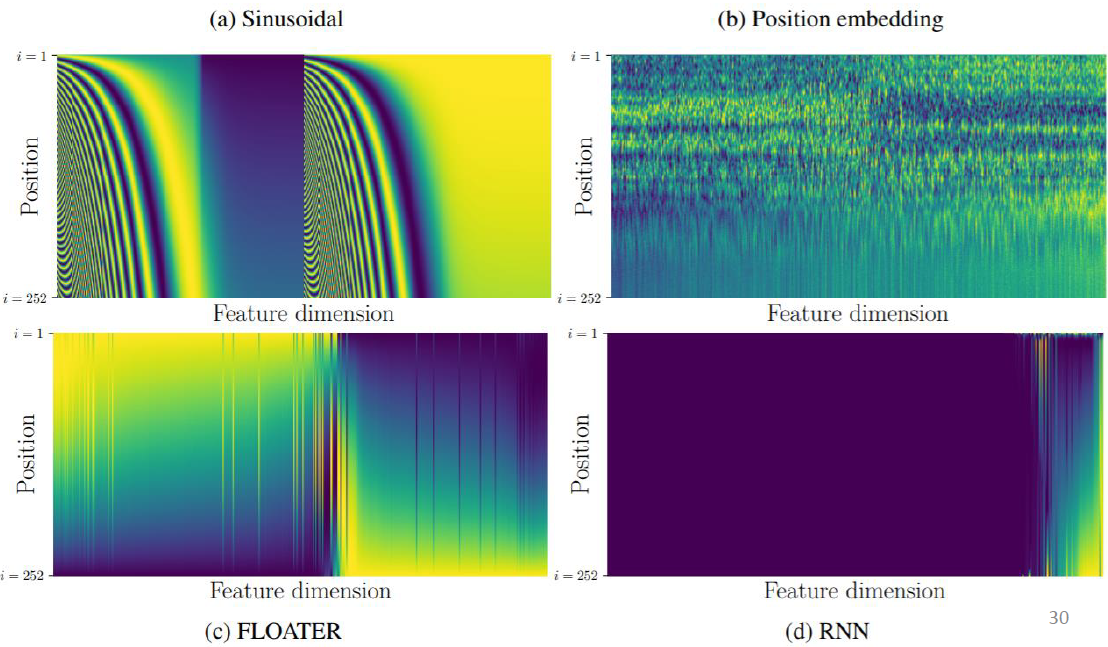
比如下图 18a 就是 sin-cos 的固定位置编码。图 b 就是可学习的位置编码。图 c 和 d 分别 FLOATER 和 RNN 模型学习的位置编码。
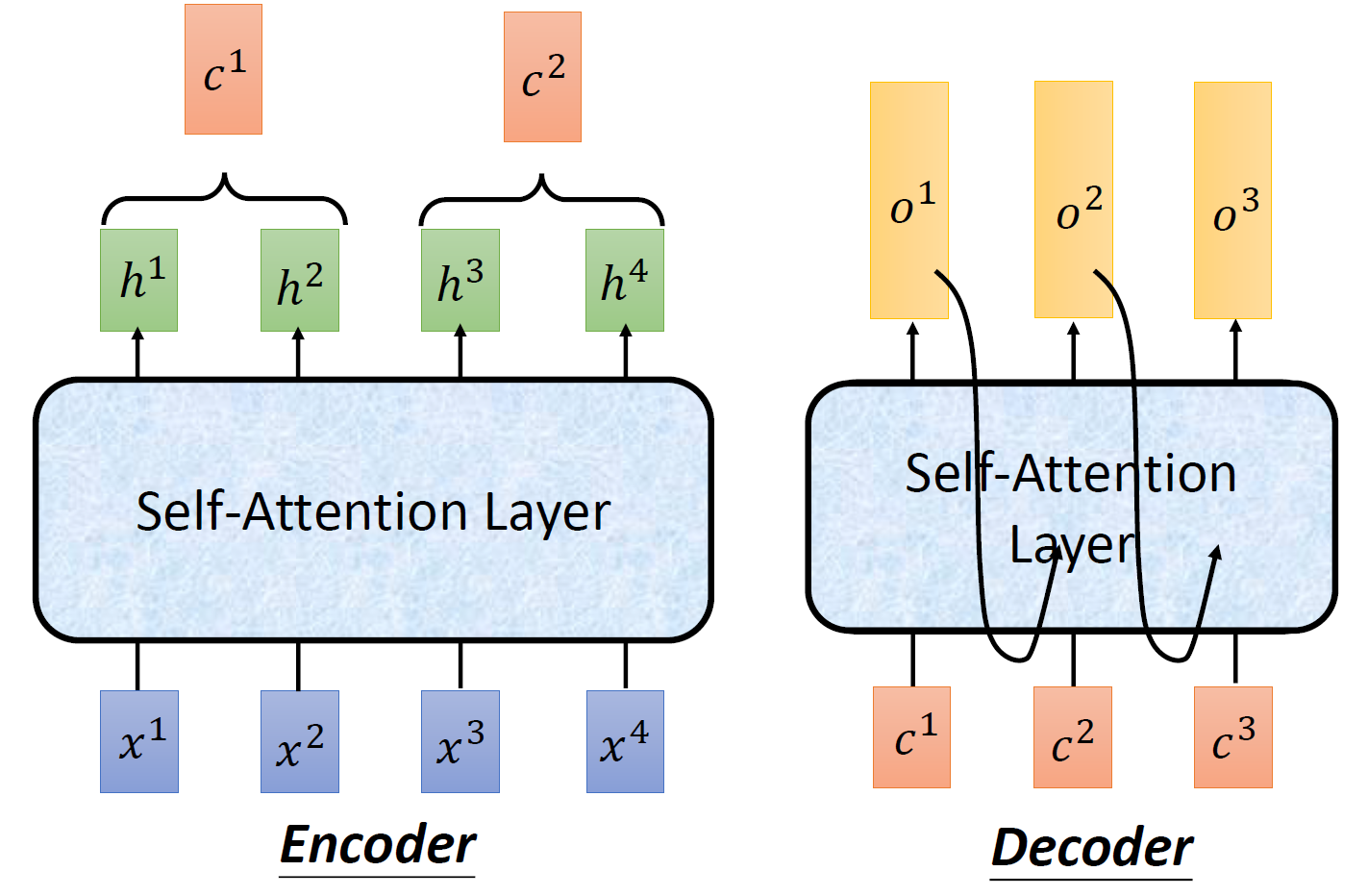
接下来我们看看 self-attention 在 sequence2sequence model 里面是怎么使用的,我们可以把 Encoder-Decoder 中的 RNN 用 self-attention 取代掉。
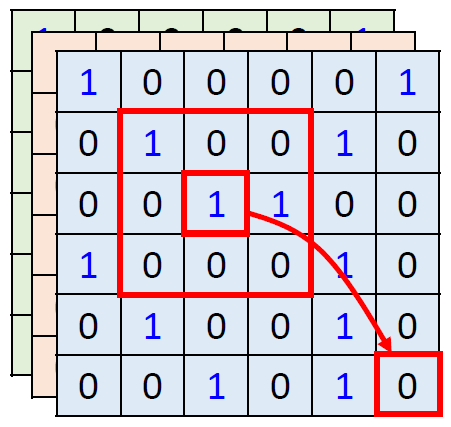
在 self-attention 的最后一部分我们来对比下 self-attention 和 CNN 的关系。如图 19,今天在使用 self-attention 去处理一张图片的时候,1 的那个 pixel 产生 query,其他的各个 pixel 产生 key。在做 inner-product 的时候,考虑的不是一个小的范围,而是一整张图片。
但是在做 CNN 的时候是只考虑感受野红框里面的资讯,而不是图片的全局信息。所以 CNN 可以看作是一种简化版本的 self-attention。
或者可以反过来说,self-attention 是一种复杂化的 CNN,在做 CNN 的时候是只考虑感受野红框里面的资讯,而感受野的范围和大小是由人决定的。但是 self-attention 由 attention 找到相关的 pixel,就好像是感受野的范围和大小是自动被学出来的,所以 CNN 可以看做是 self-attention 的特例,如图 20 所示。
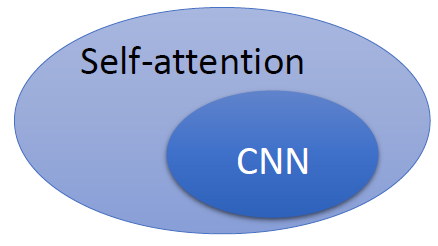
既然 self-attention 是更广义的 CNN,则这个模型更加 flexible。而我们认为,一个模型越 flexible,训练它所需要的数据量就越多,所以在训练 self-attention 模型时就需要更多的数据,这一点在下面介绍的论文 ViT 中有印证,它需要的数据集是有 3 亿张图片的 JFT-300,而如果不使用这么多数据而只使用 ImageNet,则性能不如 CNN。
2 Transformer 的实现和代码解读¶
- 2.1 Transformer 原理分析:
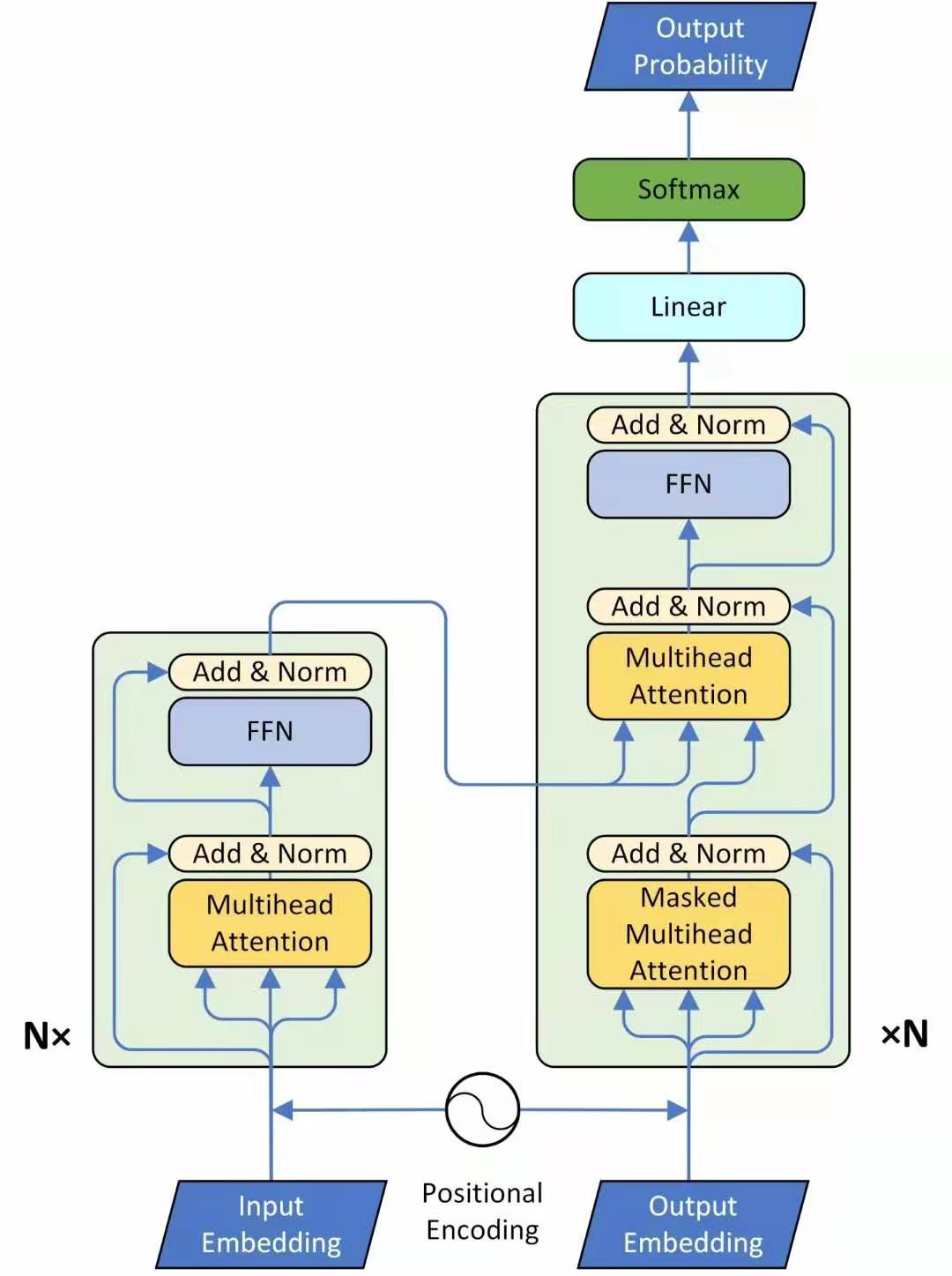
Encoder:
这个图 21 讲的是一个 seq2seq 的 model,左侧为 Encoder block,右侧为 Decoder block。红色圈中的部分为 Multi-Head Attention,是由多个 Self-Attention 组成的,可以看到 Encoder block 包含一个 Multi-Head Attention,而 Decoder block 包含两个 Multi-Head Attention (其中有一个用到 Masked)。Multi-Head Attention 上方还包括一个 Add & Norm 层,Add 表示残差连接 (Residual Connection) 用于防止网络退化,Norm 表示 Layer Normalization,用于对每一层的激活值进行归一化。比如说在 Encoder Input 处的输入是机器学习,在 Decoder Input 处的输入是 < BOS>,输出是 machine。再下一个时刻在 Decoder Input 处的输入是 machine,输出是 learning。不断重复知道输出是句点 (.) 代表翻译结束。
接下来我们看看这个 Encoder 和 Decoder 里面分别都做了什么事情,先看左半部分的 Encoder:首先输入 \(X\in R (n_x,N)\) 通过一个 Input Embedding 的转移矩阵 \(W^X\in R (d,n_x)\) 变为了一个张量,即上文所述的 \(I\in R (d,N)\) ,再加上一个表示位置的 Positional Encoding \(E\in R (d,N)\) ,得到一个张量,去往后面的操作。
它进入了这个绿色的 block,这个绿色的 block 会重复 \(N\) 次。这个绿色的 block 里面有什么呢?它的第 1 层是一个上文讲的 multi-head 的 attention。你现在一个 sequence \(I\in R (d,N)\) ,经过一个 multi-head 的 attention,你会得到另外一个 sequence \(O\in R (d,N)\) 。
下一个 Layer 是 Add & Norm,这个意思是说:把 multi-head 的 attention 的 layer 的输入 \(I\in R (d,N)\) 和输出 \(O\in R (d,N)\) 进行相加以后,再做 Layer Normalization,至于 Layer Normalization 和我们熟悉的 Batch Normalization 的区别是什么,请参考图 20 和 21。
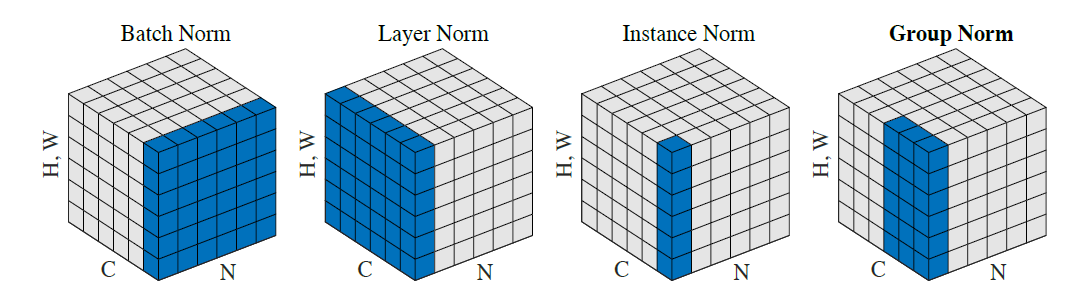
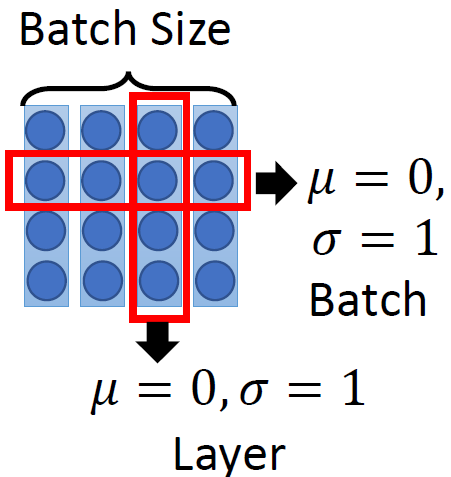
其中,Batch Normalization 和 Layer Normalization 的对比可以概括为图 22,Batch Normalization 强行让一个 batch 的数据的某个 channel 的 \(\mu=0,\sigma=1\) ,而 Layer Normalization 让一个数据的所有 channel 的 \(\mu=0,\sigma=1\) 。
接着是一个 Feed Forward 的前馈网络和一个 Add & Norm Layer。
所以,这一个绿色的 block 的前 2 个 Layer 操作的表达式为:
这一个绿色的 block 的后 2 个 Layer 操作的表达式为:
所以 Transformer 的 Encoder 的整体操作为:
\(\color{purple}{\text{Encoder}}(\color{darkgreen}{I})=\color{darkgreen}{\text{Block}}(...\color{darkgreen}{\text{Block}}(\color{darkgreen}{\text{Block}})(\color{teal}{I}))\\\quad N\;times \tag{9}\)
Decoder:
现在来看 Decoder 的部分,输入包括 2 部分,下方是前一个 time step 的输出的 embedding,即上文所述的 \(I\in R (d,N)\) ,再加上一个表示位置的 Positional Encoding \(E\in R (d,N)\) ,得到一个张量,去往后面的操作。它进入了这个绿色的 block,这个绿色的 block 会重复 \(N\) 次。这个绿色的 block 里面有什么呢?
首先是 Masked Multi-Head Self-attention,masked 的意思是使 attention 只会 attend on 已经产生的 sequence,这个很合理,因为还没有产生出来的东西不存在,就无法做 attention。
输出是: 对应 \(\color{crimson}{i}\) 位置的输出词的概率分布。
输入是: \(\color{purple}{Encoder}\) 的输出 和 对应 \(\color{crimson}{i-1}\) 位置 decoder 的输出。所以中间的 attention 不是 self-attention,它的 Key 和 Value 来自 encoder,Query 来自上一位置 \(\color{crimson}{Decoder}\) 的输出。
解码:这里要特别注意一下,编码可以并行计算,一次性全部 Encoding 出来,但解码不是一次把所有序列解出来的,而是像 \(RNN\) 一样一个一个解出来的,因为要用上一个位置的输入当作 attention 的 query。
明确了解码过程之后最上面的图就很好懂了,这里主要的不同就是新加的另外要说一下新加的 attention 多加了一个 mask,因为训练时的 output 都是 Ground Truth,这样可以确保预测第 \(\color{crimson}{i}\) 个位置时不会接触到未来的信息。
- 包含两个 Multi-Head Attention 层。
- 第一个 Multi-Head Attention 层采用了 Masked 操作。
- 第二个 Multi-Head Attention 层的 Key,Value 矩阵使用 Encoder 的编码信息矩阵 \(C\) 进行计算,而 Query 使用上一个 Decoder block 的输出计算。
- 最后有一个 Softmax 层计算下一个翻译单词的概率。
下面详细介绍下 Masked Multi-Head Self-attention 的具体操作,Masked 在 Scale 操作之后,softmax 操作之前。
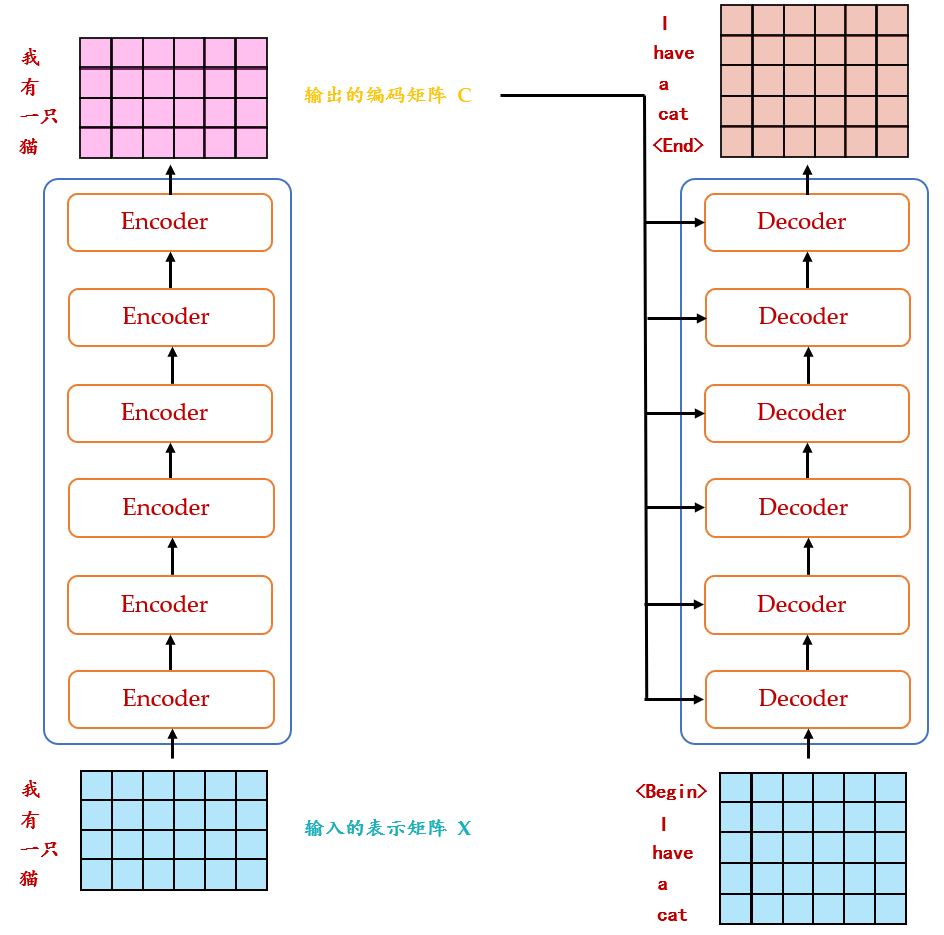
因为在翻译的过程中是顺序翻译的,即翻译完第 \(i\) 个单词,才可以翻译第 \(i+1\) 个单词。通过 Masked 操作可以防止第 \(i\) 个单词知道第 \(i+1\) 个单词之后的信息。下面以 "我有一只猫" 翻译成 "I have a cat" 为例,了解一下 Masked 操作。在 Decoder 的时候,是需要根据之前的翻译,求解当前最有可能的翻译,如下图所示。首先根据输入 "
Decoder 可以在训练的过程中使用 Teacher Forcing 并且并行化训练,即将正确的单词序列 (

注意这里 transformer 模型训练和测试的方法不同:
测试时:
- 输入
,解码器输出 I 。 - 输入前面已经解码的
和 I,解码器输出 have。 - 输入已经解码的
,I, have, a, cat,解码器输出解码结束标志位 < end>,每次解码都会利用前面已经解码输出的所有单词嵌入信息。
Transformer 测试时的解码过程:
训练时:
不采用上述类似 RNN 的方法一个一个目标单词嵌入向量顺序输入训练,想采用类似编码器中的矩阵并行算法,一步就把所有目标单词预测出来。要实现这个功能就可以参考编码器的操作,把目标单词嵌入向量组成矩阵一次输入即可。即:并行化训练。
但是在解码 have 时候,不能利用到后面单词 a 和 cat 的目标单词嵌入向量信息,否则这就是作弊 (测试时候不可能能未卜先知)。为此引入 mask。具体是:在解码器中,self-attention 层只被允许处理输出序列中更靠前的那些位置,在 softmax 步骤前,它会把后面的位置给隐去。
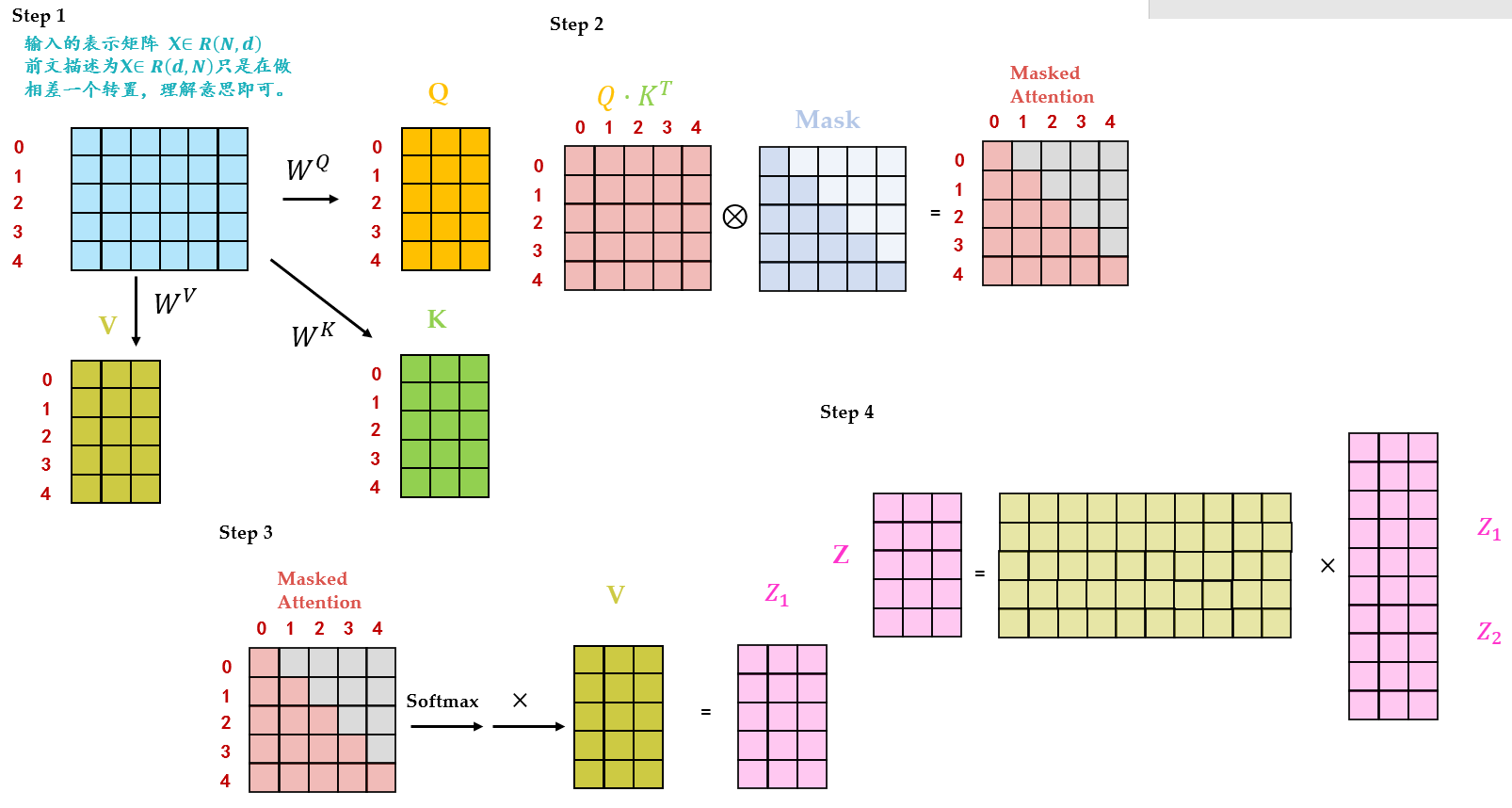
Masked Multi-Head Self-attention 的具体操作如图 26 所示。
Step1:输入矩阵包含 "
Step2: \(Q^T\cdot K\) 得到 Attention 矩阵 \(A\in R_{N,N}\) ,此时先不急于做 softmax 的操作,而是先于一个 \(\text{Mask}\in R_{N,N}\) 矩阵相乘,使得 attention 矩阵的有些位置 归 0,得到 Masked Attention 矩阵 \(\text{Mask Attention}\in R_{N,N}\) 。 \(\text{Mask}\in R_{N,N}\) 矩阵是个下三角矩阵,为什么这样设计?是因为想在计算 \(Z\) 矩阵的某一行时,只考虑它前面 token 的作用。即:在计算 \(Z\) 的第一行时,刻意地把 \(\text{Attention}\) 矩阵第一行的后面几个元素屏蔽掉,只考虑 \(\text{Attention}_{0,0}\) 。在产生 have 这个单词时,只考虑 I,不考虑之后的 have a cat,即只会 attend on 已经产生的 sequence,这个很合理,因为还没有产生出来的东西不存在,就无法做 attention。
Step3:Masked Attention 矩阵进行 Softmax,每一行的和都为 1。但是单词 0 在单词 1, 2, 3, 4 上的 attention score 都为 0。得到的结果再与 \(V\) 矩阵相乘得到最终的 self-attention 层的输出结果 \(Z_1\in R_{N,d}\) 。
Step4: \(Z_1\in R_{N,d}\) 只是某一个 head 的结果,将多个 head 的结果 concat 在一起之后再最后进行 Linear Transformation 得到最终的 Masked Multi-Head Self-attention 的输出结果 \(Z\in R_{N,d}\) 。
第 1 个 Masked Multi-Head Self-attention 的 \(\text{Query, Key, Value}\) 均来自 Output Embedding。
第 2 个 Multi-Head Self-attention 的 \(\text{Query}\) 来自第 1 个 Self-attention layer 的输出, \(\text{Key, Value}\) 来自 Encoder 的输出。
为什么这么设计?这里提供一种个人的理解:
\(\text{Key, Value}\) 来自 Transformer Encoder 的输出,所以可以看做句子 (Sequence)/ 图片 (image) 的内容信息 (content,比如句意是:"我有一只猫",图片内容是:"有几辆车,几个人等等")。
\(\text{Query}\) 表达了一种诉求:希望得到什么,可以看做引导信息 (guide)。
通过 Multi-Head Self-attention 结合在一起的过程就相当于是把我们需要的内容信息指导表达出来。
Decoder 的最后是 Softmax 预测输出单词。因为 Mask 的存在,使得单词 0 的输出 \(Z(0,)\) 只包含单词 0 的信息。Softmax 根据输出矩阵的每一行预测下一个单词,如下图 27 所示。

如下图 28 所示为 Transformer 的整体结构。
- 2.2 Transformer 代码解读:
代码来自:
https://github.com/jadore801120/attention-is-all-you-need-pytorchScaledDotProductAttention:
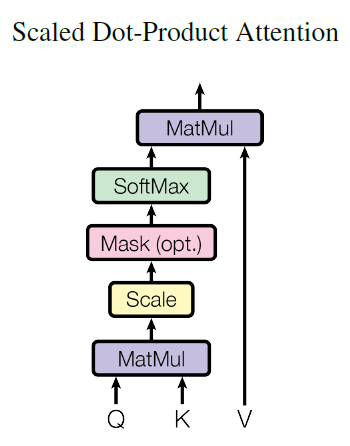
实现的是图 22 的操作,先令 \(Q\cdot K^T\) ,再对结果按位乘以 \(\text{Mask}\) 矩阵,再做 \(\text{Softmax}\) 操作,最后的结果与 \(V\) 相乘,得到 self-attention 的输出。
class ScaledDotProductAttention(nn.Module):
''' Scaled Dot-Product Attention '''
def __init__(self, temperature, attn_dropout=0.1):
super().__init__()
self.temperature = temperature
self.dropout = nn.Dropout(attn_dropout)
def forward(self, q, k, v, mask=None):
attn = torch.matmul(q / self.temperature, k.transpose(2, 3))
if mask is not None:
attn = attn.masked_fill(mask == 0, -1e9)
attn = self.dropout(F.softmax(attn, dim=-1))
output = torch.matmul(attn, v)
return output, attn
位置编码 PositionalEncoding:
实现的是式 (5) 的位置编码。
class PositionalEncoding(nn.Module):
def __init__(self, d_hid, n_position=200):
super(PositionalEncoding, self).__init__()
# Not a parameter
self.register_buffer('pos_table', self._get_sinusoid_encoding_table(n_position, d_hid))
def _get_sinusoid_encoding_table(self, n_position, d_hid):
''' Sinusoid position encoding table '''
# TODO: make it with torch instead of numpy
def get_position_angle_vec(position):
return [position / np.power(10000, 2 * (hid_j // 2) / d_hid) for hid_j in range(d_hid)]
sinusoid_table = np.array([get_position_angle_vec(pos_i) for pos_i in range(n_position)])
sinusoid_table[:, 0::2] = np.sin(sinusoid_table[:, 0::2]) # dim 2i
sinusoid_table[:, 1::2] = np.cos(sinusoid_table[:, 1::2]) # dim 2i+1
return torch.FloatTensor(sinusoid_table).unsqueeze(0)#(1,N,d)
def forward(self, x):
# x(B,N,d)
return x + self.pos_table[:, :x.size(1)].clone().detach()
MultiHeadAttention:
实现图 13,14 的多头 self-attention。
class MultiHeadAttention(nn.Module):
''' Multi-Head Attention module '''
def __init__(self, n_head, d_model, d_k, d_v, dropout=0.1):
super().__init__()
self.n_head = n_head
self.d_k = d_k
self.d_v = d_v
self.w_qs = nn.Linear(d_model, n_head * d_k, bias=False)
self.w_ks = nn.Linear(d_model, n_head * d_k, bias=False)
self.w_vs = nn.Linear(d_model, n_head * d_v, bias=False)
self.fc = nn.Linear(n_head * d_v, d_model, bias=False)
self.attention = ScaledDotProductAttention(temperature=d_k ** 0.5)
self.dropout = nn.Dropout(dropout)
self.layer_norm = nn.LayerNorm(d_model, eps=1e-6)
def forward(self, q, k, v, mask=None):
d_k, d_v, n_head = self.d_k, self.d_v, self.n_head
sz_b, len_q, len_k, len_v = q.size(0), q.size(1), k.size(1), v.size(1)
residual = q
# Pass through the pre-attention projection: b x lq x (n*dv)
# Separate different heads: b x lq x n x dv
q = self.w_qs(q).view(sz_b, len_q, n_head, d_k)
k = self.w_ks(k).view(sz_b, len_k, n_head, d_k)
v = self.w_vs(v).view(sz_b, len_v, n_head, d_v)
# Transpose for attention dot product: b x n x lq x dv
q, k, v = q.transpose(1, 2), k.transpose(1, 2), v.transpose(1, 2)
if mask is not None:
mask = mask.unsqueeze(1) # For head axis broadcasting.
q, attn = self.attention(q, k, v, mask=mask)
#q (sz_b,n_head,N=len_q,d_k)
#k (sz_b,n_head,N=len_k,d_k)
#v (sz_b,n_head,N=len_v,d_v)
# Transpose to move the head dimension back: b x lq x n x dv
# Combine the last two dimensions to concatenate all the heads together: b x lq x (n*dv)
q = q.transpose(1, 2).contiguous().view(sz_b, len_q, -1)
#q (sz_b,len_q,n_head,N * d_k)
q = self.dropout(self.fc(q))
q += residual
q = self.layer_norm(q)
return q, attn
前向传播 Feed Forward Network:
class PositionwiseFeedForward(nn.Module):
''' A two-feed-forward-layer module '''
def __init__(self, d_in, d_hid, dropout=0.1):
super().__init__()
self.w_1 = nn.Linear(d_in, d_hid) # position-wise
self.w_2 = nn.Linear(d_hid, d_in) # position-wise
self.layer_norm = nn.LayerNorm(d_in, eps=1e-6)
self.dropout = nn.Dropout(dropout)
def forward(self, x):
residual = x
x = self.w_2(F.relu(self.w_1(x)))
x = self.dropout(x)
x += residual
x = self.layer_norm(x)
return x
EncoderLayer:
实现图 26 中的一个 EncoderLayer,具体的结构如图 19 所示。
class EncoderLayer(nn.Module):
''' Compose with two layers '''
def __init__(self, d_model, d_inner, n_head, d_k, d_v, dropout=0.1):
super(EncoderLayer, self).__init__()
self.slf_attn = MultiHeadAttention(n_head, d_model, d_k, d_v, dropout=dropout)
self.pos_ffn = PositionwiseFeedForward(d_model, d_inner, dropout=dropout)
def forward(self, enc_input, slf_attn_mask=None):
enc_output, enc_slf_attn = self.slf_attn(
enc_input, enc_input, enc_input, mask=slf_attn_mask)
enc_output = self.pos_ffn(enc_output)
return enc_output, enc_slf_attn
DecoderLayer:
实现图 28 中的一个 DecoderLayer,具体的结构如图 21 所示。
class DecoderLayer(nn.Module):
''' Compose with three layers '''
def __init__(self, d_model, d_inner, n_head, d_k, d_v, dropout=0.1):
super(DecoderLayer, self).__init__()
self.slf_attn = MultiHeadAttention(n_head, d_model, d_k, d_v, dropout=dropout)
self.enc_attn = MultiHeadAttention(n_head, d_model, d_k, d_v, dropout=dropout)
self.pos_ffn = PositionwiseFeedForward(d_model, d_inner, dropout=dropout)
def forward(
self, dec_input, enc_output,
slf_attn_mask=None, dec_enc_attn_mask=None):
dec_output, dec_slf_attn = self.slf_attn(
dec_input, dec_input, dec_input, mask=slf_attn_mask)
dec_output, dec_enc_attn = self.enc_attn(
dec_output, enc_output, enc_output, mask=dec_enc_attn_mask)
dec_output = self.pos_ffn(dec_output)
return dec_output, dec_slf_attn, dec_enc_attn
Encoder:
实现图 28,21 左侧的 Encoder:
class Encoder(nn.Module):
''' A encoder model with self attention mechanism. '''
def __init__(
self, n_src_vocab, d_word_vec, n_layers, n_head, d_k, d_v,
d_model, d_inner, pad_idx, dropout=0.1, n_position=200):
super().__init__()
self.src_word_emb = nn.Embedding(n_src_vocab, d_word_vec, padding_idx=pad_idx)
self.position_enc = PositionalEncoding(d_word_vec, n_position=n_position)
self.dropout = nn.Dropout(p=dropout)
self.layer_stack = nn.ModuleList([
EncoderLayer(d_model, d_inner, n_head, d_k, d_v, dropout=dropout)
for _ in range(n_layers)])
self.layer_norm = nn.LayerNorm(d_model, eps=1e-6)
def forward(self, src_seq, src_mask, return_attns=False):
enc_slf_attn_list = []
# -- Forward
enc_output = self.dropout(self.position_enc(self.src_word_emb(src_seq)))
enc_output = self.layer_norm(enc_output)
for enc_layer in self.layer_stack:
enc_output, enc_slf_attn = enc_layer(enc_output, slf_attn_mask=src_mask)
enc_slf_attn_list += [enc_slf_attn] if return_attns else []
if return_attns:
return enc_output, enc_slf_attn_list
return enc_output,
Decoder:
实现图 28,21 右侧的 Decoder:
class Decoder(nn.Module):
''' A decoder model with self attention mechanism. '''
def forward(self, trg_seq, trg_mask, enc_output, src_mask, return_attns=False):
dec_slf_attn_list, dec_enc_attn_list = [], []
# -- Forward
dec_output = self.dropout(self.position_enc(self.trg_word_emb(trg_seq)))
dec_output = self.layer_norm(dec_output)
for dec_layer in self.layer_stack:
dec_output, dec_slf_attn, dec_enc_attn = dec_layer(
dec_output, enc_output, slf_attn_mask=trg_mask, dec_enc_attn_mask=src_mask)
dec_slf_attn_list += [dec_slf_attn] if return_attns else []
dec_enc_attn_list += [dec_enc_attn] if return_attns else []
if return_attns:
return dec_output, dec_slf_attn_list, dec_enc_attn_list
return dec_output,
整体结构:
实现图 28,21 整体的 Transformer:
class Transformer(nn.Module):
''' A sequence to sequence model with attention mechanism. '''
def __init__(
self, n_src_vocab, n_trg_vocab, src_pad_idx, trg_pad_idx,
d_word_vec=512, d_model=512, d_inner=2048,
n_layers=6, n_head=8, d_k=64, d_v=64, dropout=0.1, n_position=200,
trg_emb_prj_weight_sharing=True, emb_src_trg_weight_sharing=True):
super().__init__()
self.src_pad_idx, self.trg_pad_idx = src_pad_idx, trg_pad_idx
self.encoder = Encoder(
n_src_vocab=n_src_vocab, n_position=n_position,
d_word_vec=d_word_vec, d_model=d_model, d_inner=d_inner,
n_layers=n_layers, n_head=n_head, d_k=d_k, d_v=d_v,
pad_idx=src_pad_idx, dropout=dropout)
self.decoder = Decoder(
n_trg_vocab=n_trg_vocab, n_position=n_position,
d_word_vec=d_word_vec, d_model=d_model, d_inner=d_inner,
n_layers=n_layers, n_head=n_head, d_k=d_k, d_v=d_v,
pad_idx=trg_pad_idx, dropout=dropout)
self.trg_word_prj = nn.Linear(d_model, n_trg_vocab, bias=False)
for p in self.parameters():
if p.dim() > 1:
nn.init.xavier_uniform_(p)
assert d_model == d_word_vec, \
'To facilitate the residual connections, \
the dimensions of all module outputs shall be the same.'
self.x_logit_scale = 1.
if trg_emb_prj_weight_sharing:
# Share the weight between target word embedding & last dense layer
self.trg_word_prj.weight = self.decoder.trg_word_emb.weight
self.x_logit_scale = (d_model ** -0.5)
if emb_src_trg_weight_sharing:
self.encoder.src_word_emb.weight = self.decoder.trg_word_emb.weight
def forward(self, src_seq, trg_seq):
src_mask = get_pad_mask(src_seq, self.src_pad_idx)
trg_mask = get_pad_mask(trg_seq, self.trg_pad_idx) & get_subsequent_mask(trg_seq)
enc_output, *_ = self.encoder(src_seq, src_mask)
dec_output, *_ = self.decoder(trg_seq, trg_mask, enc_output, src_mask)
seq_logit = self.trg_word_prj(dec_output) * self.x_logit_scale
return seq_logit.view(-1, seq_logit.size(2))
产生 Mask:
def get_pad_mask(seq, pad_idx):
return (seq != pad_idx).unsqueeze(-2)
def get_subsequent_mask(seq):
''' For masking out the subsequent info. '''
sz_b, len_s = seq.size()
subsequent_mask = (1 - torch.triu(
torch.ones((1, len_s, len_s), device=seq.device), diagonal=1)).bool()
return subsequent_mask
src_mask = get_pad_mask(src_seq, self.src_pad_idx)
用于产生 Encoder 的 Mask,它是一列 Bool 值,负责把标点 mask 掉。
trg_mask = get_pad_mask(trg_seq, self.trg_pad_idx) & get_subsequent_mask(trg_seq)
用于产生 Decoder 的 Mask。它是一个矩阵,如图 24 中的 Mask 所示,功能已在上文介绍。
3 Transformer+Detection:引入视觉领域的首创 DETR¶
论文名称:End-to-End Object Detection with Transformers
论文地址:
https://arxiv.org/abs/2005.12872
- 3.1 DETR 原理分析:
\(\color{indianred}{\text{网络架构部分解读:}}\)
本文的任务是 Object detection,用到的工具是 Transformers,特点是 End-to-end。
目标检测的任务是要去预测一系列的 Bounding Box 的坐标以及 Label, 现代大多数检测器通过定义一些 proposal,anchor 或者 windows,把问题构建成为一个分类和回归问题来间接地完成这个任务。文章所做的工作,就是将 transformers 运用到了 object detection 领域,取代了现在的模型需要手工设计的工作,并且取得了不错的结果。在 object detection 上 DETR 准确率和运行时间上和 Faster RCNN 相当;将模型 generalize 到 panoptic segmentation 任务上,DETR 表现甚至还超过了其他的 baseline。DETR 第一个使用 End to End 的方式解决检测问题,解决的方法是把检测问题视作是一个 set prediction problem,如下图 29 所示。

网络的主要组成是 CNN 和 Transformer,Transformer 借助第 1 节讲到的 self-attention 机制,可以显式地对一个序列中的所有 elements 两两之间的 interactions 进行建模,使得这类 transformer 的结构非常适合带约束的 set prediction 的问题。DETR 的特点是:一次预测,端到端训练,set loss function 和二分匹配。
文章的主要有两个关键的部分。
第一个是用 transformer 的 encoder-decoder 架构一次性生成 \(N\) 个 box prediction。其中 \(N\) 是一个事先设定的、比远远大于 image 中 object 个数的一个整数。
第二个是设计了 bipartite matching loss,基于预测的 boxex 和 ground truth boxes 的二分图匹配计算 loss 的大小,从而使得预测的 box 的位置和类别更接近于 ground truth。
DETR 整体结构可以分为四个部分:backbone,encoder,decoder 和 FFN,如下图 30 所示,以下分别解释这四个部分:
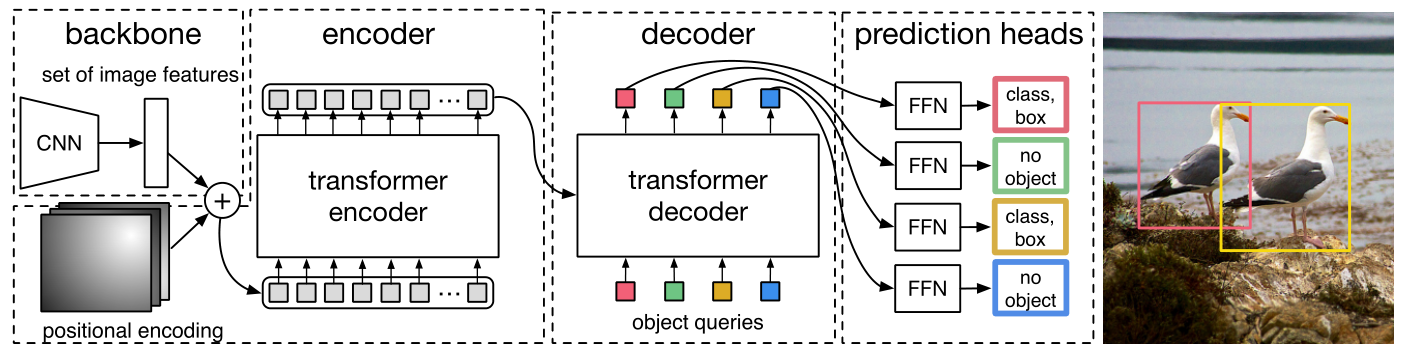
1 首先看 backbone:CNN backbone 处理 \(x_{\text{img}}\in B\times 3\times H_0 \times W_0\) 维的图像,把它转换为\(f\in R^{B\times C\times H\times W}\) 维的 feature map(一般来说 \(C = 2048或256, H = \frac{H_0}{32}, W = \frac{W_0}{32}\)),backbone 只做这一件事。
2 再看 encoder:encoder 的输入是\(f\in R^{B\times C\times H\times W}\) 维的 feature map,接下来依次进行以下过程:
- 通道数压缩:先用 \(1\times 1\) convolution 处理,将 channels 数量从 \(C\) 压缩到 \(d\),即得到\(z_0\in R^{B\times d\times H\times W}\) 维的新 feature map。
- 转化为序列化数据:将空间的维度(高和宽)压缩为一个维度,即把上一步得到的\(z_0\in R^{B\times d\times H\times W}(d=256)\) 维的 feature map 通过 reshape 成\((HW,B,256)\) 维的 feature map。
- 位置编码:在得到了\(z_0\in R^{B\times d\times H\times W}\) 维的 feature map 之后,正式输入 encoder 之前,需要进行 Positional Encoding。这一步在第 2 节讲解 transformer 的时候已经提到过,因为在 self-attention 中需要有表示位置的信息,否则你的 sequence = "A 打了 B" 还是 sequence = "B 打了 A" 的效果是一样的。但是 transformer encoder 这个结构本身却无法体现出位置信息。也就是说,我们需要对这个 \(z_0\in R^{B\times d\times H\times W}\) 维的 feature map 做 positional encoding。
进行完位置编码以后根据 paper 中的图片会有个相加的过程,如下图问号处所示。很多读者有疑问的地方是:论文图 31 示中相加的 2 个张量,一个是 input embedding,另一个是位置编码维度看上去不一致,是怎么相加的?后面会解答。
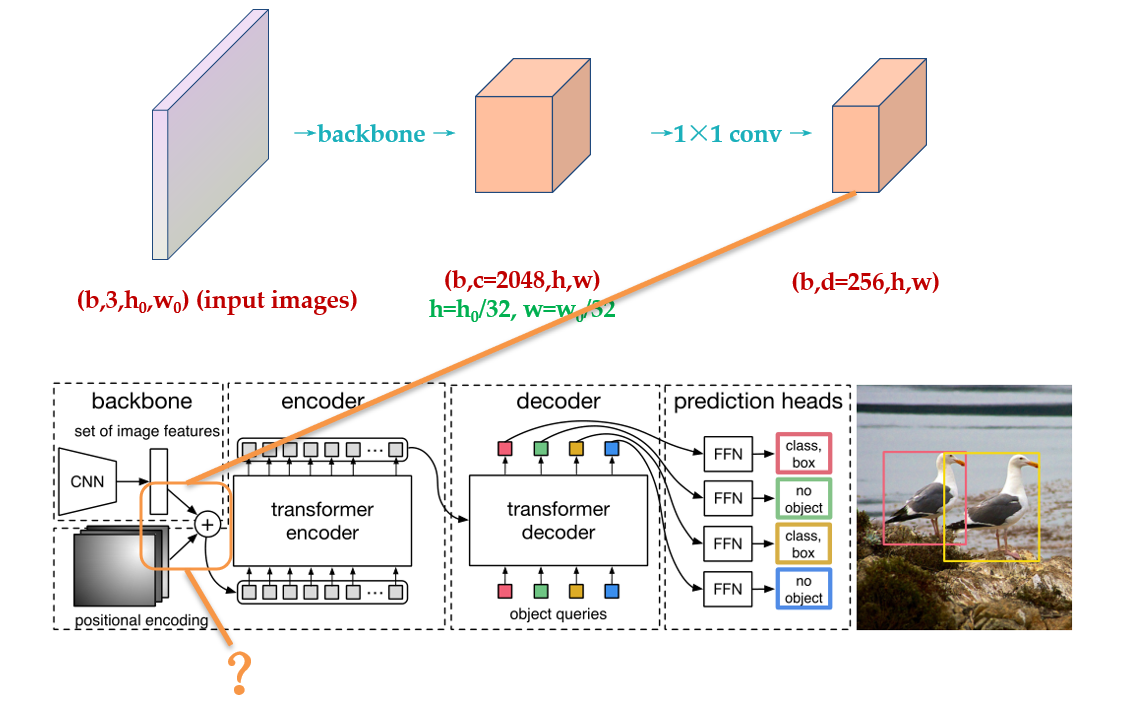
原版 Transformer 和 Vision Transformer (第 4 节讲述) 的 Positional Encoding 的表达式为:
式中, \(d\) 就是这个 \(d\times HW\) 维的 feature map 的第一维, \(pos\in [1,HW]\) 。表示 token 在 sequence 中的位置,sequence 的长度是 \(HW\) ,例如第一个 token 的 \(pos=0\) 。
\(i\) ,或者准确意义上是 \(2i\) 和 \(2i+1\) 表示了 Positional Encoding 的维度,\(i\) 的取值范围是: \(\left[ 0,\ldots ,{{{d}}}/{2}\; \right)\) 。所以当 \(pos\) 为 1 时,对应的 Positional Encoding 可以写成:
\(PE\left( 1 \right)=\left[ \sin \left( {1}/{{{10000}^{{0}/{256}\;}}}\; \right),\cos \left( {1}/{{{10000}^{{0}/{256}\;}}}\; \right),\sin \left( {1}/{{{10000}^{{2}/{256}\;}}}\; \right),\cos \left( {1}/{{{10000}^{{2}/{256}\;}}}\; \right),\ldots \right]\)
式中, \({{d}_{}}=256\)。
第一点不同的是,原版 Transformer 只考虑 \(x\) 方向的位置编码,但是 DETR 考虑了 \(xy\) 方向的位置编码,因为图像特征是 2-D 特征。采用的依然是 \(\text{sin cos}\) 模式,但是需要考虑 \(xy\) 两个方向。不是类似 vision transoformer 做法简单的将其拉伸为 \(d\times HW\) ,然后从 \([1,HW]\) 进行长度为 256 的位置编码,而是考虑了 \(xy\) 方向同时编码,每个方向各编码 128 维向量,这种编码方式更符合图像特点。
Positional Encoding 的输出张量是: \((B,d,H,W),d=256\) ,其中 \(d\) 代表位置编码的长度, \(H,W\) 代表张量的位置。意思是说,这个特征图上的任意一个点 \((H_1,W_1)\) 有个位置编码,这个编码的长度是 256,其中,前 128 维代表 \(H_1\) 的位置编码,后 128 维代表 \(W_1\) 的位置编码。
假设你想计算任意一个位置 \((pos_x,pos_y),pos_x\in [1,HW],pos_y\in [1,HW]\) 的 Positional Encoding,把 \(pos_x\) 代入 (11) 式的 \(a\) 式和 \(b\) 式可以计算得到 128 维的向量,它代表 \(pos_x\) 的位置编码,再把 \(pos_y\) 代入 (11) 式的 \(c\) 式和 \(d\) 式可以计算得到 128 维的向量,它代表 \(pos_y\) 的位置编码,把这 2 个 128 维的向量拼接起来,就得到了一个 256 维的向量,它代表 \((pos_x,pos_y)\) 的位置编码。
计算所有位置的编码,就得到了 \((256,H,W)\) 的张量,代表这个 batch 的位置编码。编码矩阵的维度是 \((B,256,H,W)\) ,也把它序列化成维度为 \((HW,B,256)\) 维的张量。
准备与\((HW,B,256)\) 维的 feature map 相加以后输入 Encoder。
值得注意的是,网上许多解读文章没有搞清楚 "转化为序列化数据" 这一步和 "位置编码" 的顺序关系,以及变量的 shape 到底是怎样变化的,这里我用一个图 32 表达,终结这个问题。
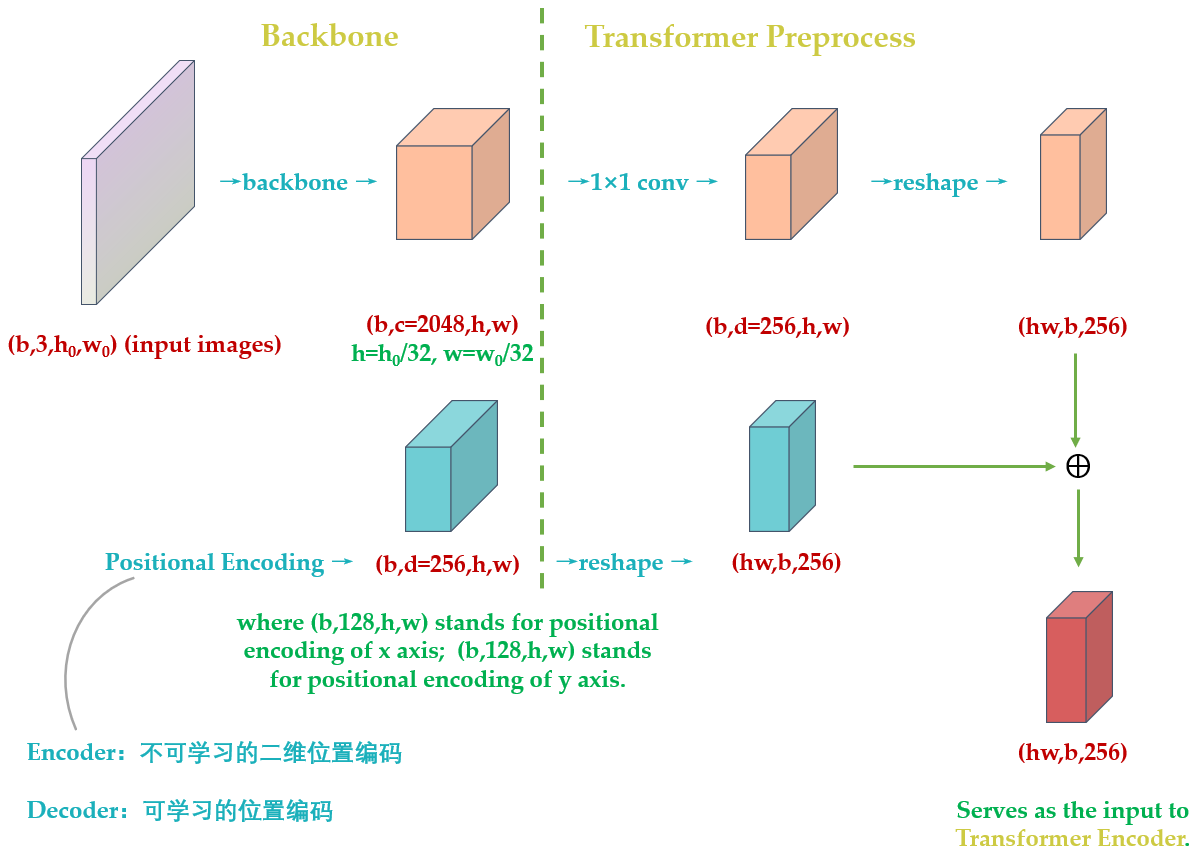
所以,了解了 DETR 的位置编码之后,你应该明白了其实 input embedding 和位置编码维度其实是一样的,只是论文图示为了突出二位编码所以画的不一样罢了,如下图 33 所示:
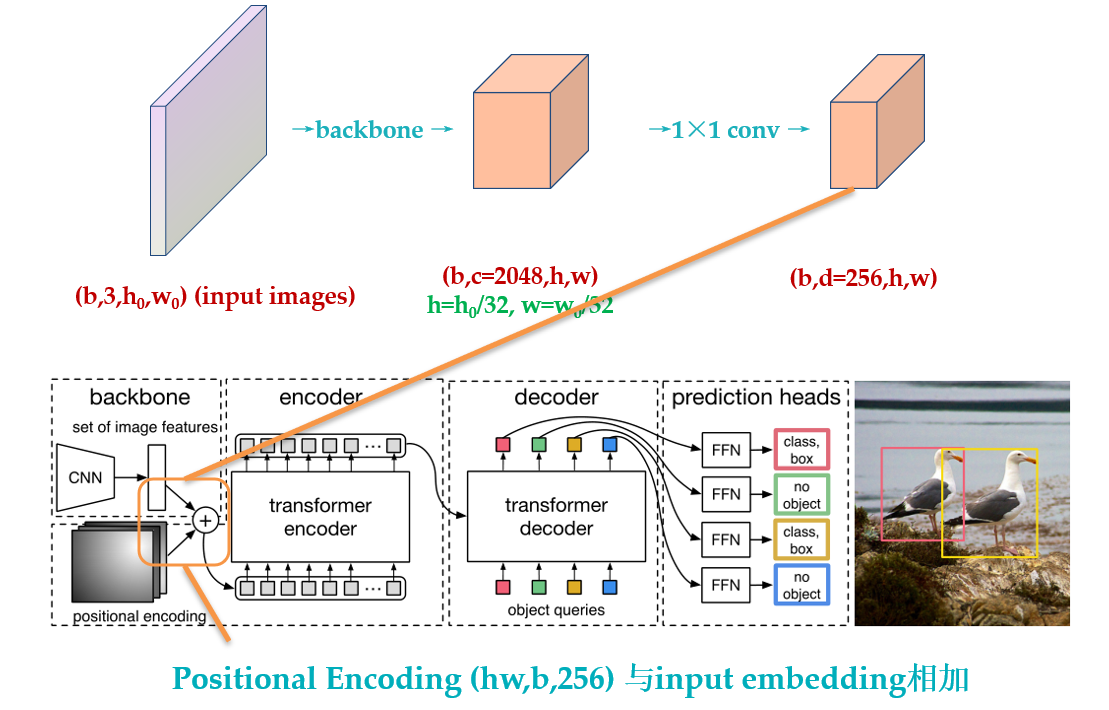
另一点不同的是,原版 Transformer 只在 Encoder 之前使用了 Positional Encoding,而且是在输入上进行 Positional Encoding,再把输入经过 transformation matrix 变为 Query,Key 和 Value 这几个张量。但是 DETR 在 Encoder 的每一个 Multi-head Self-attention 之前都使用了 Positional Encoding,且只对 Query 和 Key 使用了 Positional Encoding,即:只把维度为\((HW,B,256)\) 维的位置编码与维度为\((HW,B,256)\) 维的 Query 和 Key 相加,而不与 Value 相加。
如图 34 所示为 DETR 的 Transformer 的详细结构,读者可以对比下原版 Transformer 的结构,如图 21 所示,为了阅读的方便我把图 21 又贴在下面了。
可以发现,除了 Positional Encoding 设置的不一样外,Encoder 其他的结构是一致的。每个 Encoder Layer 包含一个 multi-head self-attention 的 module 和一个前馈网络 Feed Forward Network。
Encoder 最终输出的是 \((H\cdot W,b,256)\) 维的编码矩阵 Embedding,按照原版 Transformer 的做法,把这个东西给 Decoder。
总结下和原始 transformer 编码器不同的地方:
- 输入编码器的位置编码需要考虑 2-D 空间位置。
- 位置编码向量需要加入到每个 Encoder Layer 中。
- 在编码器内部位置编码 Positional Encoding 仅仅作用于 Query 和 Key,即只与 Query 和 Key 相加,Value 不做任何处理。
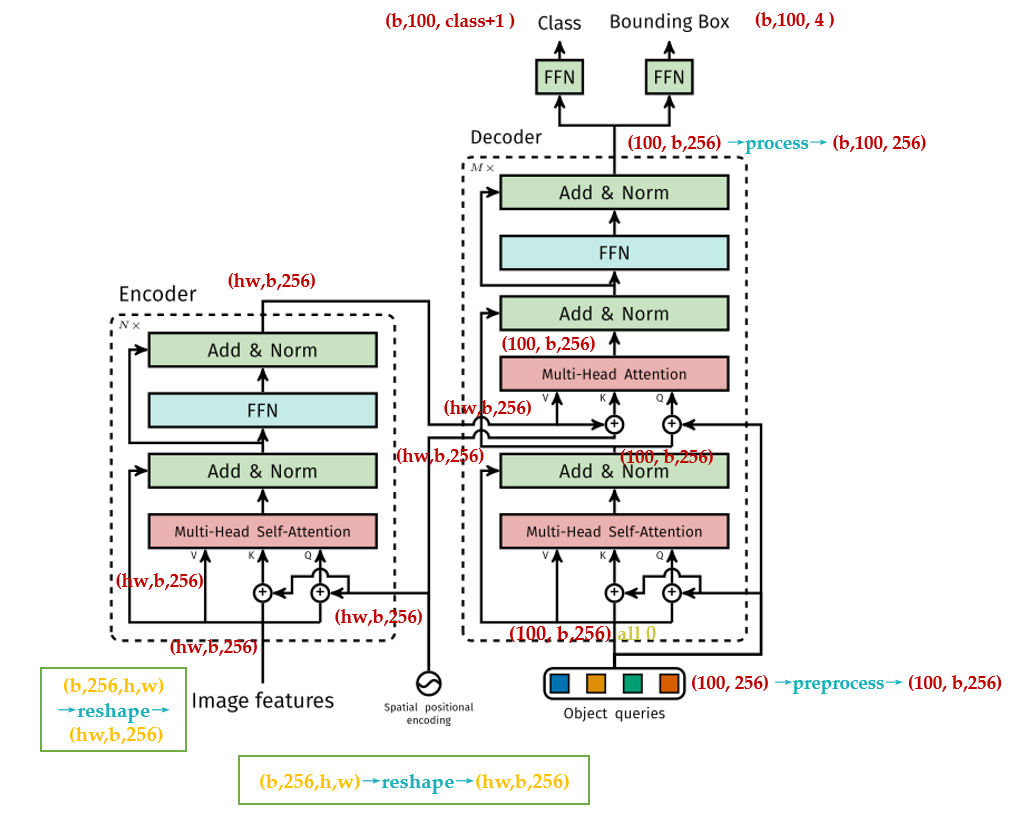

3 再看 decoder:
DETR 的 Decoder 和原版 Transformer 的 decoder 是不太一样的,如下图 34 和 21 所示。
先回忆下原版 Transformer,看下图 21 的 decoder 的最后一个框:output probability,代表我们一次只产生一个单词的 softmax,根据这个 softmax 得到这个单词的预测结果。这个过程我们表达为:predicts the output sequence one element at a time。
不同的是,DETR 的 Transformer Decoder 是一次性处理全部的 object queries,即一次性输出全部的 predictions;而不像原始的 Transformer 是 auto-regressive 的,从左到右一个词一个词地输出。这个过程我们表达为:decodes the N objects in parallel at each decoder layer。
DETR 的 Decoder 主要有两个输入:
- Transformer Encoder 输出的 Embedding 与 position encoding 之和。
- Object queries。
其中,Embedding 就是上文提到的 \((H\cdot W,b,256)\) 的编码矩阵。这里着重讲一下 Object queries。
Object queries 是一个维度为 \((100,b,256)\) 维的张量,数值类型是 nn.Embedding,说明这个张量是可以学习的,即:我们的 Object queries 是可学习的。Object queries 矩阵内部通过学习建模了 100 个物体之间的全局关系,例如房间里面的桌子旁边 (A 类) 一般是放椅子(B 类),而不会是放一头大象(C 类),那么在推理时候就可以利用该全局注意力更好的进行解码预测输出。
Decoder 的输入一开始也初始化成维度为 \((100,b,256)\) 维的全部元素都为 0 的张量,和 Object queries 加在一起之后充当第 1 个 multi-head self-attention 的 Query 和 Key。第一个 multi-head self-attention 的 Value 为 Decoder 的输入,也就是全 0 的张量。
到了每个 Decoder 的第 2 个 multi-head self-attention,它的 Key 和 Value 来自 Encoder 的输出张量,维度为 \((hw,b,256)\) ,其中 Key 值还进行位置编码。Query 值一部分来自第 1 个 Add and Norm 的输出,维度为 \((100,b,256)\) 的张量,另一部分来自 Object queries,充当可学习的位置编码。所以,第 2 个 multi-head self-attention 的 Key 和 Value 的维度为 \((hw,b,256)\) ,而 Query 的维度为\((100,b,256)\)。
每个 Decoder 的输出维度为 \((1,b,100,256)\) ,送入后面的前馈网络,具体的变量维度的变化见图 30。
到这里你会发现:Object queries 充当的其实是位置编码的作用,只不过它是可以学习的位置编码,所以,我们对 Encoder 和 Decoder 的每个 self-attention 的 Query 和 Key 的位置编码做个归纳,如图 35 所示,Value 没有位置编码:

\(\color{indianred}{\text{损失函数部分解读:}}\)
得到了 Decoder 的输出以后,如前文所述,应该是输出维度为 \((b,100,256)\) 的张量。接下来要送入 2 个前馈网络 FFN 得到 class 和 Bounding Box。它们会得到 \(N=100\) 个预测目标,包含类别和 Bounding Box,当然这个 100 肯定是大于图中的目标总数的。如果不够 100,则采用背景填充,计算 loss 时候回归分支分支仅仅计算有物体位置,背景集合忽略。所以,DETR 输出张量的维度为输出的张量的维度是 \((b,100,\color{crimson}{\text{class}+1})\) 和 \((b,100,\color{purple}{4})\)。对应 COCO 数据集来说, \(\color{crimson}{\text{class}+1=92}\) , \(\color{purple}{4}\) 指的是每个预测目标归一化的 \((c_x,c_y,w,h)\) 。归一化就是除以图片宽高进行归一化。
到这里我们了解了 DETR 的网络架构,我们发现,它输出的张量的维度是 分类分支:\((b,100,\color{crimson}{\text{class}+1})\) 和回归分支: \((b,100,\color{purple}{4})\) ,其中,前者是指 100 个预测框的类型,后者是指 100 个预测框的 Bounding Box,但是读者可能会有疑问:预测框和真值是怎么一一对应的?换句话说:你怎么知道第 47 个预测框对应图片里的狗,第 88 个预测框对应图片里的车?等等。
我们下面就来聊聊这个问题。
相比 Faster R-CNN 等做法,DETR 最大特点是将目标检测问题转化为无序集合预测问题 (set prediction)。论文中特意指出 Faster R-CNN 这种设置一大堆 anchor,然后基于 anchor 进行分类和回归其实属于代理做法即不是最直接做法,目标检测任务就是输出无序集合,而 Faster R-CNN 等算法通过各种操作,并结合复杂后处理最终才得到无序集合属于绕路了,而 DETR 就比较纯粹了。现在核心问题来了:输出的 \((b,100)\) 个检测结果是无序的,如何和 \(GT \; \text{Bounding Box}\) 计算 loss?这就需要用到经典的双边匹配算法了,也就是常说的匈牙利算法,该算法广泛应用于最优分配问题。
一幅图片,我们把第 \(i\) 个物体的真值表达为 \(y_i=(c_i,b_i)\) ,其中, \(c_i\) 表示它的 \(\color{crimson}{\text{class}}\) , \(b_i\) 表示它的 \(\color{purple}{\text{Bounding Box}}\) 。我们定义 \(\hat y = \{\hat y_i\}_{i=1}^{N}\) 为网络输出的 \(N\) 个预测值。
假设我们已经了解了什么是匈牙利算法 (先假装了解了),对于第 \(i\) 个 \(GT\) , \(\sigma(i)\) 为匈牙利算法得到的与 \(GT_i\) 对应的 prediction 的索引。我举个栗子,比如 \(i=3,\sigma(i)=18\) ,意思就是:与第 3 个真值对应的预测值是第 18 个。
那我能根据 \(\color{green}{\text{匈牙利算法}}\) ,找到 \(\color{green}{\text{与每个真值对应的预测值是哪个}}\) ,那究竟是如何找到呢?
我们看看这个表达式是甚么意思,对于某一个真值 \(y_i\) ,假设我们已经找到这个真值对应的预测值 \(\hat y_{\sigma(i)}\) ,这里的 \(\Sigma_N\) 是所有可能的排列,代表从真值索引到预测值索引的所有的映射,然后用 \(L_{match}\) 最小化 \(y_i\) 和 \(\hat y_{\sigma(i)}\) 的距离。这个 \(L_{match}\) 具体是:
意思是:假设当前从真值索引到预测值索引的所有的映射为 \(\sigma\) ,对于图片中的每个真值 \(i\) ,先找到对应的预测值 \(\sigma(i)\) ,再看看分类网络的结果 \(\hat p_{\sigma(i)}(c_i)\) ,取反作为 \(L_{match}\) 的第 1 部分。再计算回归网络的结果 \(\hat b_{\sigma(i)}\) 与真值的 \(\color{purple}{\text{Bounding Box}}\) 的差异,即 \(L_{box}({b_{i}, \hat b_{\sigma(i)}})\) ,作为 \(L_{match}\) 的第 2 部分。
所以,可以使得 \(L_{match}\) 最小的排列 \(\hat\sigma\) 就是我们要找的排列,即:对于图片中的每个真值 \(i\) 来讲, \(\hat\sigma(i)\) 就是这个真值所对应的预测值的索引。
请读者细品这个 寻找匹配的过程 ,这就是匈牙利算法的过程。是不是与 Anchor 或 Proposal 有异曲同工的地方,只是此时我们找的是一对一匹配。
接下来就是使用上一步得到的排列 \(\hat\sigma\) ,计算匈牙利损失:
式中的 \(L_{box}\) 具体为:
最常用的 \(L_1 \;loss\) 对于大小 \(\color{purple}{\text{Bounding Box}}\) 会有不同的标度,即使它们的相对误差是相似的。为了缓解这个问题,作者使用了 \(L_1 \;loss\) 和广义 IoU 损耗 \(L_{iou}\) 的线性组合,它是比例不变的。
Hungarian 意思就是匈牙利,也就是前面的 \(L_{match}\) ,上述意思是需要计算 \(M\) 个 \(\text{GT}\;\color{purple}{\text{Bounding Box}}\) 和 \(N\) 个输预测出集合两两之间的广义距离,距离越近表示越可能是最优匹配关系,也就是两者最密切。广义距离的计算考虑了分类分支和回归分支。
最后,再概括一下 DETR 的 End-to-End 的原理,前面那么多段话就是为了讲明白这个事情,如果你对前面的论述还存在疑问的话,把下面一直到 Experiments 之前的这段话看懂就能解决你的困惑。
DETR 是怎么训练的?
训练集里面的任何一张图片,假设第 1 张图片,我们通过模型产生 100 个预测框 \(\text{Predict}\;\color{purple}{\text{Bounding Box}}\) ,假设这张图片有只 3 个 \(\text{GT}\;\color{purple}{\text{Bounding Box}}\) ,它们分别是 \(\color{orange}{\text{Car}},\color{green}{\text{Dog}},\color{darkturquoise}{\text{Horse}}\) 。
问题是:我怎么知道这 100 个预测框哪个是对应 \(\color{orange}{\text{Car}}\) ,哪个是对应 \(\color{green}{\text{Dog}}\) ,哪个是对应 \(\color{darkturquoise}{\text{Horse}}\) ?
我们建立一个 \((100,3)\) 的矩阵,矩阵里面的元素就是 \((13)\) 式的计算结果,举个例子:比如左上角的 \((1,1)\) 号元素的含义是:第 1 个预测框对应 \(\color{orange}{\text{Car}}(\text{label}=3)\) 的情况下的 \(L_{match}\) 值。我们用 scipy.optimize 这个库中的 linear_sum_assignment 函数找到最优的匹配,这个过程我们称之为:"匈牙利算法 (Hungarian Algorithm)"。
假设 linear_sum_assignment 做完以后的结果是:第 \(23\) 个预测框对应 \(\color{orange}{\text{Car}}\) ,第 \(44\) 个预测框对应 \(\color{green}{\text{Dog}}\) ,第 \(95\) 个预测框对应 \(\color{darkturquoise}{\text{Horse}}\) 。
现在把第 \(23,44,95\) 个预测框挑出来,按照 \((14)\) 式计算 Loss,得到这个图片的 Loss。
把所有的图片按照这个模式去训练模型。
训练完以后怎么用?
训练完以后,你的模型学习到了一种能力,即:模型产生的 100 个预测框,它知道某个预测框该对应什么 \(\text{Object}\) ,比如,模型学习到:第 1 个 \(\text{Predict}\;\color{purple}{\text{Bounding Box}}\) 对应 \(\color{orange}{\text{Car}}(\text{label}=3)\) ,第 2 个 \(\text{Predict}\;\color{purple}{\text{Bounding Box}}\) 对应 \(\color{chocolate}{\text{Bus}}(\text{label}=16)\) ,第 3 个 \(\text{Predict}\;\color{purple}{\text{Bounding Box}}\) 对应 \(\color{lightskyblue}{\text{Sky}}(\text{label}=21)\) ,第 4 个 \(\text{Predict}\;\color{purple}{\text{Bounding Box}}\) 对应 \(\color{green}{\text{Dog}}(\text{label}=24)\) ,第 5 个 \(\text{Predict}\;\color{purple}{\text{Bounding Box}}\) 对应 \(\color{darkturquoise}{\text{Horse}}(\text{label}=75)\) ,第 6-100 个 \(\text{Predict}\;\color{purple}{\text{Bounding Box}}\) 对应 \(\color{dimgray}{\varnothing }(\text{label}=92)\) ,等等。
以上只是我举的一个例子,意思是说:模型知道了自己的 100 个预测框每个该做什么事情,即:每个框该预测什么样的 \(\text{Object}\) 。
为什么训练完以后,模型学习到了一种能力,即:模型产生的 100 个预测框,它知道某个预测框该对应什么 \(\text{Object}\) ?
还记得前面说的 Object queries 吗?它是一个维度为 \((100,b,256)\) 维的张量,初始时元素全为 \(0\) 。实现方式是 nn.Embedding(num_queries, hidden_dim),这里 num_queries=100,hidden_dim=256,它是可训练的。这里的 \(b\) 指的是 batch size,我们考虑单张图片,所以假设 Object queries 是一个维度为 \((100,256)\) 维的张量。我们训练完模型以后,这个张量已经训练完了,那此时的 Object queries 究竟代表什么?
我们把此时的 Object queries 看成 100 个格子,每个格子是个 256 维的向量。训练完以后,这 100 个格子里面注入了不同 \(\text{Object}\) 的位置信息和类别信息。比如第 1 个格子里面的这个 256 维的向量代表着 \(\color{orange}{\text{Car}}\) 这种 \(\text{Object}\) 的位置信息,这种信息是通过训练,考虑了所有图片的某个位置附近的 \(\color{orange}{\text{Car}}\) 编码特征,属于和位置有关的全局 \(\color{orange}{\text{Car}}\) 统计信息。
测试时,假设图片中有 \(\color{orange}{\text{Car}},\color{green}{\text{Dog}},\color{darkturquoise}{\text{Horse}}\) 三种物体,该图片会输入到编码器中进行特征编码,假设特征没有丢失,Decoder 的 Key 和 Value 就是编码器输出的编码向量 (如图 30 所示),而 Query 就是 Object queries,就是我们的 100 个格子。
Query 可以视作代表不同 \(\text{Object}\) 的信息,而 Key 和 Value 可以视作代表图像的全局信息。
现在通过注意力模块将 Query 和 Key 计算,然后加权 Value 得到解码器输出。对于第 1 个格子的 Query 会和 Key 中的所有向量进行计算,目的是查找某个位置附近有没有 \(\color{orange}{\text{Car}}\) ,如果有那么该特征就会加权输出,对于第 3 个格子的 Query 会和 Key 中的所有向量进行计算,目的是查找某个位置附近有没有 \(\color{lightskyblue}{\text{Sky}}\) ,很遗憾,这个没有,所以输出的信息里面没有 \(\color{lightskyblue}{\text{Sky}}\) 。
整个过程计算完成后就可以把编码向量中的 \(\color{orange}{\text{Car}},\color{green}{\text{Dog}},\color{darkturquoise}{\text{Horse}}\) 的编码嵌入信息提取出来,然后后面接 \(FFN\) 进行分类和回归就比较容易,因为特征已经对齐了。
发现了吗?Object queries 在训练过程中对于 \(N\) 个格子会压缩入对应的和位置和类别相关的统计信息,在测试阶段就可以利用该 Query 去和某个图像的编码特征 Key,Value 计算,若图片中刚好有 Query 想找的特征,比如 \(\color{orange}{\text{Car}}\) ,则这个特征就能提取出来,最后通过 2 个 \(FFN\) 进行分类和回归。所以前面才会说 Object queries 作用非常类似 Faster R-CNN 中的 anchor,这个 anchor 是可学习的,由于维度比较高,故可以表征的东西丰富,当然维度越高,训练时长就会越长。
这就是 DETR 的 End-to-End 的原理,可以简单归结为上面的几段话,你读懂了上面的话,也就明白了 DETR 以及 End-to-End 的 Detection 模型原理。
Experiments:
1. 性能对比:
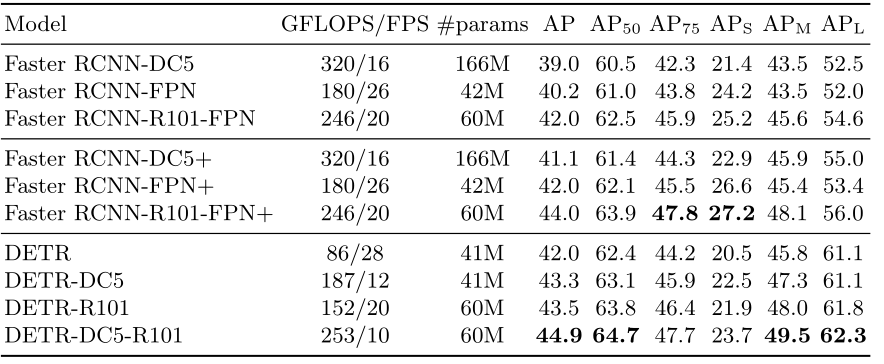
2. 编码器层数对比实验:
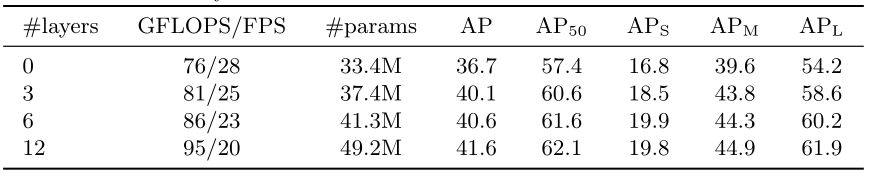
可以发现,编码器层数越多越好,最后就选择 6。
下图 38 为最后一个 Encoder Layer 的 attention 可视化,Encoder 已经分离了 instances,简化了 Decoder 的对象提取和定位。

3. 解码器层数对比实验:
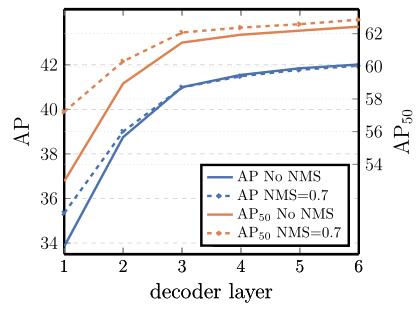
可以发现,性能随着解码器层数的增加而提升,DETR 本不需要 NMS,但是作者也进行了,上图中的 NMS 操作是指 DETR 的每个解码层都可以输入无序集合,那么将所有解码器无序集合全部保留,然后进行 NMS 得到最终输出,可以发现性能稍微有提升,特别是 AP50。这可以通过以下事实来解释:Transformer 的单个 Decoder Layer 不能计算输出元素之间的任何互相关,因此它易于对同一对象进行多次预测。在第 2 个和随后的 Decoder Layer 中,self-attention 允许模型抑制重复预测。所以 NMS 带来的改善随着 Decoder Layer 的增加而减少。在最后几层,作者观察到 AP 的一个小损失,因为 NMS 错误地删除了真实的 positive prediction。

类似于可视化编码器注意力,作者在图 40 中可视化解码器注意力,用不同的颜色给每个预测对象的注意力图着色。观察到,解码器的 attention 相当局部,这意味着它主要关注对象的四肢,如头部或腿部。我们假设,在编码器通过全局关注分离实例之后,解码器只需要关注极端来提取类和对象边界。
- 3.2 DETR 代码解读:
https://github.com/facebookresearch/detr
分析都注释在了代码中。
二维位置编码:
DETR 的二维位置编码:
首先构造位置矩阵 x_embed 和 y_embed,这里用到了 python 函数 cumsum,作用是对一个矩阵的元素进行累加,那么累加以后最后一个元素就是所有累加元素的和,省去了求和的步骤,直接用这个和做归一化,对应 x_embed[:, :, -1:] 和 y_embed[:, -1:, :]。
这里我想着重强调下代码中一些变量的 shape,方便读者掌握作者编程的思路:
值得注意的是,tensor_list 的类型是 NestedTensor,内部自动附加了 mask,用于表示动态 shape,是 pytorch 中 tensor 新特性 https://github.com/pytorch/nestedtensor。全是 false。
x:(b,c,H,W)
mask:(b,H,W),全是 False。
not_mask:(b,H,W),全是 True。
首先出现的 y_embed:(b,H,W),具体是 1,1,1,1,......,2,2,2,2,......3,3,3,3,......
首先出现的 x_embed:(b,H,W),具体是 1,2,3,4,......,1,2,3,4,......1,2,3,4,......
self.num_pos_feats = 128
首先出现的 dim_t = [0,1,2,3,.....,127]
pos_x:(b,H,W,128)
pos_y:(b,H,W,128)
flatten 后面的数字指的是:flatten() 方法应从哪个轴开始展开操作。
torch.stack((pos_x[:, :, :, 0::2].sin(), pos_x[:, :, :, 1::2].cos()), dim=4).flatten(3)
pos_y = torch.stack((pos_y[:, :, :, 0::2].sin(), pos_y[:, :, :, 1::2].cos()), dim=4)
这一步执行完以后变成 (b,H,W,2,64) 通过 flatten()方法从第 3 个轴开始展平,变为:(b,H,W,128)
torch.cat((pos_y, pos_x), dim=3) 之后变为 (b,H,W,256),再最后 permute 为 (b,256,H,W)。
PositionEmbeddingSine 类继承 nn.Module 类。
class PositionEmbeddingSine(nn.Module):
def forward(self, tensor_list: NestedTensor):
#输入是b,c,h,w
#tensor_list的类型是NestedTensor,内部自动附加了mask,
#用于表示动态shape,是pytorch中tensor新特性https://github.com/pytorch/nestedtensor
x = tensor_list.tensors
# 附加的mask,shape是b,h,w 全是false
mask = tensor_list.mask
assert mask is not None
not_mask = ~mask
# 因为图像是2d的,所以位置编码也分为x,y方向
# 1 1 1 1 .. 2 2 2 2... 3 3 3...
y_embed = not_mask.cumsum(1, dtype=torch.float32)
# 1 2 3 4 ... 1 2 3 4...
x_embed = not_mask.cumsum(2, dtype=torch.float32)
if self.normalize:
eps = 1e-6
y_embed = y_embed / (y_embed[:, -1:, :] + eps) * self.scale
x_embed = x_embed / (x_embed[:, :, -1:] + eps) * self.scale
# num_pos_feats = 128
# 0~127 self.num_pos_feats=128,因为前面输入向量是256,编码是一半sin,一半cos
dim_t = torch.arange(self.num_pos_feats, dtype=torch.float32, device=x.device)
dim_t = self.temperature ** (2 * (dim_t // 2) / self.num_pos_feats)
# 输出shape=b,h,w,128
pos_x = x_embed[:, :, :, None] / dim_t
pos_y = y_embed[:, :, :, None] / dim_t
pos_x = torch.stack((pos_x[:, :, :, 0::2].sin(), pos_x[:, :, :, 1::2].cos()), dim=4).flatten(3)
pos_y = torch.stack((pos_y[:, :, :, 0::2].sin(), pos_y[:, :, :, 1::2].cos()), dim=4).flatten(3)
pos = torch.cat((pos_y, pos_x), dim=3).permute(0, 3, 1, 2)
# 每个特征图的xy位置都编码成256的向量,其中前128是y方向编码,而128是x方向编码
return pos
# b,n=256,h,w
作者定义了一种数据结构:NestedTensor,里面打包存了两个变量:x 和 mask。
NestedTensor:
里面打包存了两个变量:x 和 mask。
to() 函数:把变量移到 GPU 中。Backbone:
class BackboneBase(nn.Module):
def __init__(self, backbone: nn.Module, train_backbone: bool, num_channels: int, return_interm_layers: bool):
super().__init__()
for name, parameter in backbone.named_parameters():
if not train_backbone or 'layer2' not in name and 'layer3' not in name and 'layer4' not in name:
parameter.requires_grad_(False)
if return_interm_layers:
return_layers = {"layer1": "0", "layer2": "1", "layer3": "2", "layer4": "3"}
else:
return_layers = {'layer4': "0"}
#作用的模型:定义BackboneBase时传入的nn.Moduleclass的backbone,返回的layer:来自bool变量return_interm_layers
self.body = IntermediateLayerGetter(backbone, return_layers=return_layers)
self.num_channels = num_channels
def forward(self, tensor_list: NestedTensor):
#BackboneBase的输入是一个NestedTensor
#xs中间层的输出,
xs = self.body(tensor_list.tensors)
out: Dict[str, NestedTensor] = {}
for name, x in xs.items():
m = tensor_list.mask
assert m is not None
#F.interpolate上下采样,调整mask的size
#to(torch.bool) 把mask转化为Bool型变量
mask = F.interpolate(m[None].float(), size=x.shape[-2:]).to(torch.bool)[0]
out[name] = NestedTensor(x, mask)
return out
class Backbone(BackboneBase):
"""ResNet backbone with frozen BatchNorm."""
def __init__(self, name: str,
train_backbone: bool,
return_interm_layers: bool,
dilation: bool):
#根据name选择backbone, num_channels, return_interm_layers等,传入BackboneBase初始化
backbone = getattr(torchvision.models, name)(
replace_stride_with_dilation=[False, False, dilation],
pretrained=is_main_process(), norm_layer=FrozenBatchNorm2d)
num_channels = 512 if name in ('resnet18', 'resnet34') else 2048
super().__init__(backbone, train_backbone, num_channels, return_interm_layers)
把 Backbone 和之前的 PositionEmbeddingSine 连在一起:
Backbone 完以后输出 (b,c,h,w),再经过 PositionEmbeddingSine 输出 (b,H,W,256)。
class Joiner(nn.Sequential):
def __init__(self, backbone, position_embedding):
super().__init__(backbone, position_embedding)
def forward(self, tensor_list: NestedTensor):
xs = self[0](tensor_list)
out: List[NestedTensor] = []
pos = []
for name, x in xs.items():
out.append(x)
# position encoding
pos.append(self[1](x).to(x.tensors.dtype))
return out, pos
def build_backbone(args):
#position_embedding是个nn.module
position_embedding = build_position_encoding(args)
train_backbone = args.lr_backbone > 0
return_interm_layers = args.masks
#backbone是个nn.module
backbone = Backbone(args.backbone, train_backbone, return_interm_layers, args.dilation)
#nn.Sequential在一起
model = Joiner(backbone, position_embedding)
model.num_channels = backbone.num_channels
return model
Transformer 的一个 Encoder Layer:
class TransformerEncoderLayer(nn.Module):
def __init__(self, d_model, nhead, dim_feedforward=2048, dropout=0.1,
activation="relu", normalize_before=False):
super().__init__()
self.self_attn = nn.MultiheadAttention(d_model, nhead, dropout=dropout)
# Implementation of Feedforward model
self.linear1 = nn.Linear(d_model, dim_feedforward)
self.dropout = nn.Dropout(dropout)
self.linear2 = nn.Linear(dim_feedforward, d_model)
self.norm1 = nn.LayerNorm(d_model)
self.norm2 = nn.LayerNorm(d_model)
self.dropout1 = nn.Dropout(dropout)
self.dropout2 = nn.Dropout(dropout)
self.activation = _get_activation_fn(activation)
self.normalize_before = normalize_before
def with_pos_embed(self, tensor, pos: Optional[Tensor]):
return tensor if pos is None else tensor + pos
def forward_post(self,
src,
src_mask: Optional[Tensor] = None,
src_key_padding_mask: Optional[Tensor] = None,
pos: Optional[Tensor] = None):
# 和标准做法有点不一样,src加上位置编码得到q和k,但是v依然还是src,
# 也就是v和qk不一样
q = k = self.with_pos_embed(src, pos)
src2 = self.self_attn(q, k, value=src, attn_mask=src_mask,
key_padding_mask=src_key_padding_mask)[0]
#Add and Norm
src = src + self.dropout1(src2)
src = self.norm1(src)
#FFN
src2 = self.linear2(self.dropout(self.activation(self.linear1(src))))
#Add and Norm
src = src + self.dropout2(src2)
src = self.norm2(src)
return src
def forward_pre(self, src,
src_mask: Optional[Tensor] = None,
src_key_padding_mask: Optional[Tensor] = None,
pos: Optional[Tensor] = None):
src2 = self.norm1(src)
q = k = self.with_pos_embed(src2, pos)
src2 = self.self_attn(q, k, value=src2, attn_mask=src_mask,
key_padding_mask=src_key_padding_mask)[0]
src = src + self.dropout1(src2)
src2 = self.norm2(src)
src2 = self.linear2(self.dropout(self.activation(self.linear1(src2))))
src = src + self.dropout2(src2)
return src
def forward(self, src,
src_mask: Optional[Tensor] = None,
src_key_padding_mask: Optional[Tensor] = None,
pos: Optional[Tensor] = None):
if self.normalize_before:
return self.forward_pre(src, src_mask, src_key_padding_mask, pos)
return self.forward_post(src, src_mask, src_key_padding_mask, pos)
有了一个 Encoder Layer 的定义,再看 Transformer 的整个 Encoder:
class TransformerEncoder(nn.Module):
def __init__(self, encoder_layer, num_layers, norm=None):
super().__init__()
# 编码器copy6份
self.layers = _get_clones(encoder_layer, num_layers)
self.num_layers = num_layers
self.norm = norm
def forward(self, src,
mask: Optional[Tensor] = None,
src_key_padding_mask: Optional[Tensor] = None,
pos: Optional[Tensor] = None):
# 内部包括6个编码器,顺序运行
# src是图像特征输入,shape=hxw,b,256
output = src
for layer in self.layers:
# 第一个编码器输入来自图像特征,后面的编码器输入来自前一个编码器输出
output = layer(output, src_mask=mask,
src_key_padding_mask=src_key_padding_mask, pos=pos)
return output
Object Queries:可学习的位置编码:
注释中已经注明了变量的 shape 的变化过程,最终输出的是与 Positional Encoding 维度相同的位置编码,维度是 (b,H,W,256),只是现在这个位置编码是可学习的了。
class PositionEmbeddingLearned(nn.Module):
"""
Absolute pos embedding, learned.
"""
def __init__(self, num_pos_feats=256):
super().__init__()]
#这里使用了nn.Embedding,这是一个矩阵类,里面初始化了一个随机矩阵,矩阵的长是字典的大小,宽是用来表示字典中每个元素的属性向量,
# 向量的维度根据你想要表示的元素的复杂度而定。类实例化之后可以根据字典中元素的下标来查找元素对应的向量。输入下标0,输出就是embeds矩阵中第0行。
self.row_embed = nn.Embedding(50, num_pos_feats)
self.col_embed = nn.Embedding(50, num_pos_feats)
self.reset_parameters()
def reset_parameters(self):
nn.init.uniform_(self.row_embed.weight)
nn.init.uniform_(self.col_embed.weight)
#输入依旧是NestedTensor
def forward(self, tensor_list: NestedTensor):
x = tensor_list.tensors
h, w = x.shape[-2:]
i = torch.arange(w, device=x.device)
j = torch.arange(h, device=x.device)
#x_emb:(w, 128)
#y_emb:(h, 128)
x_emb = self.col_embed(i)
y_emb = self.row_embed(j)
pos = torch.cat([
x_emb.unsqueeze(0).repeat(h, 1, 1),#(1,w,128) → (h,w,128)
y_emb.unsqueeze(1).repeat(1, w, 1),#(h,1,128) → (h,w,128)
], dim=-1).permute(2, 0, 1).unsqueeze(0).repeat(x.shape[0], 1, 1, 1)
#(h,w,256) → (256,h,w) → (1,256,h,w) → (b,256,h,w)
return pos
def build_position_encoding(args):
N_steps = args.hidden_dim // 2
if args.position_embedding in ('v2', 'sine'):
# TODO find a better way of exposing other arguments
position_embedding = PositionEmbeddingSine(N_steps, normalize=True)
elif args.position_embedding in ('v3', 'learned'):
position_embedding = PositionEmbeddingLearned(N_steps)
else:
raise ValueError(f"not supported {args.position_embedding}")
return position_embedding
Transformer 的一个 Decoder Layer:
注意变量的命名:
object queries(query_pos)
Encoder 的位置编码 (pos)
Encoder 的输出 (memory)
def forward_post(self, tgt, memory,
tgt_mask: Optional[Tensor] = None,
memory_mask: Optional[Tensor] = None,
tgt_key_padding_mask: Optional[Tensor] = None,
memory_key_padding_mask: Optional[Tensor] = None,
pos: Optional[Tensor] = None,
query_pos: Optional[Tensor] = None):
#query,key的输入是object queries(query_pos) + Decoder的输入(tgt),shape都是(100,b,256)
#value的输入是Decoder的输入(tgt),shape = (100,b,256)
q = k = self.with_pos_embed(tgt, query_pos)
#Multi-head self-attention
tgt2 = self.self_attn(q, k, value=tgt, attn_mask=tgt_mask,
key_padding_mask=tgt_key_padding_mask)[0]
#Add and Norm
tgt = tgt + self.dropout1(tgt2)
tgt = self.norm1(tgt)
#query的输入是上一个attention的输出(tgt) + object queries(query_pos)
#key的输入是Encoder的位置编码(pos) + Encoder的输出(memory)
#value的输入是Encoder的输出(memory)
tgt2 = self.multihead_attn(query=self.with_pos_embed(tgt, query_pos),
key=self.with_pos_embed(memory, pos),
value=memory, attn_mask=memory_mask,
key_padding_mask=memory_key_padding_mask)[0]
#Add and Norm
tgt = tgt + self.dropout2(tgt2)
tgt = self.norm2(tgt)
#FFN
tgt2 = self.linear2(self.dropout(self.activation(self.linear1(tgt))))
tgt = tgt + self.dropout3(tgt2)
tgt = self.norm3(tgt)
return tgt
def forward_pre(self, tgt, memory,
tgt_mask: Optional[Tensor] = None,
memory_mask: Optional[Tensor] = None,
tgt_key_padding_mask: Optional[Tensor] = None,
memory_key_padding_mask: Optional[Tensor] = None,
pos: Optional[Tensor] = None,
query_pos: Optional[Tensor] = None):
tgt2 = self.norm1(tgt)
q = k = self.with_pos_embed(tgt2, query_pos)
tgt2 = self.self_attn(q, k, value=tgt2, attn_mask=tgt_mask,
key_padding_mask=tgt_key_padding_mask)[0]
tgt = tgt + self.dropout1(tgt2)
tgt2 = self.norm2(tgt)
tgt2 = self.multihead_attn(query=self.with_pos_embed(tgt2, query_pos),
key=self.with_pos_embed(memory, pos),
value=memory, attn_mask=memory_mask,
key_padding_mask=memory_key_padding_mask)[0]
tgt = tgt + self.dropout2(tgt2)
tgt2 = self.norm3(tgt)
tgt2 = self.linear2(self.dropout(self.activation(self.linear1(tgt2))))
tgt = tgt + self.dropout3(tgt2)
return tgt
def forward(self, tgt, memory,
tgt_mask: Optional[Tensor] = None,
memory_mask: Optional[Tensor] = None,
tgt_key_padding_mask: Optional[Tensor] = None,
memory_key_padding_mask: Optional[Tensor] = None,
pos: Optional[Tensor] = None,
query_pos: Optional[Tensor] = None):
if self.normalize_before:
return self.forward_pre(tgt, memory, tgt_mask, memory_mask,
tgt_key_padding_mask, memory_key_padding_mask, pos, query_pos)
return self.forward_post(tgt, memory, tgt_mask, memory_mask,
tgt_key_padding_mask, memory_key_padding_mask, pos, query_pos)
有了一个 Decoder Layer 的定义,再看 Transformer 的整个 Decoder:
class TransformerDecoder(nn.Module):
#值得注意的是:在使用TransformerDecoder时需要传入的参数有:
# tgt:Decoder的输入,memory:Encoder的输出,pos:Encoder的位置编码的输出,query_pos:Object Queries,一堆mask
def forward(self, tgt, memory,
tgt_mask: Optional[Tensor] = None,
memory_mask: Optional[Tensor] = None,
tgt_key_padding_mask: Optional[Tensor] = None,
memory_key_padding_mask: Optional[Tensor] = None,
pos: Optional[Tensor] = None,
query_pos: Optional[Tensor] = None):
output = tgt
# Decoder输入的tgt:(100, b, 256)
intermediate = []
for layer in self.layers:
output = layer(output, memory, tgt_mask=tgt_mask,
memory_mask=memory_mask,
tgt_key_padding_mask=tgt_key_padding_mask,
memory_key_padding_mask=memory_key_padding_mask,
pos=pos, query_pos=query_pos)
if self.return_intermediate:
intermediate.append(self.norm(output))
if self.norm is not None:
output = self.norm(output)
if self.return_intermediate:
intermediate.pop()
intermediate.append(output)
if self.return_intermediate:
return torch.stack(intermediate)
return output.unsqueeze(0)
然后是把 Encoder 和 Decoder 拼在一起,即总的 Transformer 结构的实现:
此处考虑到字数限制,省略了代码。实现了 Transformer,还剩后面的 FFN:
class MLP(nn.Module):
""" Very simple multi-layer perceptron (also called FFN)"""
def __init__(self, input_dim, hidden_dim, output_dim, num_layers):
super().__init__()
self.num_layers = num_layers
h = [hidden_dim] * (num_layers - 1)
self.layers = nn.ModuleList(nn.Linear(n, k) for n, k in zip([input_dim] + h, h + [output_dim]))
def forward(self, x):
for i, layer in enumerate(self.layers):
x = F.relu(layer(x)) if i < self.num_layers - 1 else layer(x)
return x
匈牙利匹配 HungarianMatcher 类:
这个类的目的是计算从 targets 到 predictions 的一种最优排列。
predictions 比 targets 的数量多,但我们要进行 1-to-1 matching,所以多的 predictions 将与 \(\varnothing\) 匹配。
这个函数整体在构建 (13) 式,cost_class,cost_bbox,cost_giou,对应的就是 (13) 式中的几个损失函数,它们的维度都是(b,100,m)。
m 包含了这个 batch 内部所有的 \(\text{GT}\;\color{purple}{\text{Bounding Box}}\) 。
# pred_logits:[b,100,92]
# pred_boxes:[b,100,4]
# targets是个长度为b的list,其中的每个元素是个字典,共包含:labels-长度为(m,)的Tensor,元素是标签;boxes-长度为(m,4)的Tensor,元素是Bounding Box。
# detr分类输出,num_queries=100,shape是(b,100,92)
bs, num_queries = outputs["pred_logits"].shape[:2]
# We flatten to compute the cost matrices in a batch
out_prob = outputs["pred_logits"].flatten(0, 1).softmax(-1) # [batch_size * num_queries, num_classes] = [100b, 92]
out_bbox = outputs["pred_boxes"].flatten(0, 1) # [batch_size * num_queries, 4] = [100b, 4]
# 准备分类target shape=(m,)里面存储的是类别索引,m包括了整个batch内部的所有gt bbox
# Also concat the target labels and boxes
tgt_ids = torch.cat([v["labels"] for v in targets])# (m,)[3,6,7,9,5,9,3]
# 准备bbox target shape=(m,4),已经归一化了
tgt_bbox = torch.cat([v["boxes"] for v in targets])# (m,4)
#(100b,92)->(100b, m),对于每个预测结果,把目前gt里面有的所有类别值提取出来,其余值不需要参与匹配
#对应上述公式,类似于nll loss,但是更加简单
# Compute the classification cost. Contrary to the loss, we don't use the NLL,
# but approximate it in 1 - proba[target class].
# The 1 is a constant that doesn't change the matching, it can be ommitted.
#行:取每一行;列:只取tgt_ids对应的m列
cost_class = -out_prob[:, tgt_ids]# (100b, m)
# Compute the L1 cost between boxes, 计算out_bbox和tgt_bbox两两之间的l1距离 (100b, m)
cost_bbox = torch.cdist(out_bbox, tgt_bbox, p=1)# (100b, m)
# Compute the giou cost betwen boxes, 额外多计算一个giou loss (100b, m)
cost_giou = -generalized_box_iou(box_cxcywh_to_xyxy(out_bbox), box_cxcywh_to_xyxy(tgt_bbox))
#得到最终的广义距离(100b, m),距离越小越可能是最优匹配
# Final cost matrix
C = self.cost_bbox * cost_bbox + self.cost_class * cost_class + self.cost_giou * cost_giou
#(100b, m)--> (b, 100, m)
C = C.view(bs, num_queries, -1).cpu()
#计算每个batch内部有多少物体,后续计算时候按照单张图片进行匹配,没必要batch级别匹配,徒增计算
sizes = [len(v["boxes"]) for v in targets]
#匈牙利最优匹配,返回匹配索引
#enumerate(C.split(sizes, -1))]:(b,100,image1,image2,image3,...)
indices = [linear_sum_assignment(c[i]) for i, c in enumerate(C.split(sizes, -1))]
return [(torch.as_tensor(i, dtype=torch.int64), torch.as_tensor(j, dtype=torch.int64)) for i, j in indices]
在得到匹配关系后算 loss 就水到渠成了。loss_labels 计算分类损失,loss_boxes 计算回归损失,包含 \(\text{L_1 loss, iou loss}\) 。
代码中的其他结构:
SmoothedValue:
一种自定义的数据结构,属于 object 类。它是 deque 类型的双向队列,通过 update(value) 进行更新。
MetricLogger:
一种自定义的数据结构,属于 object 类。它是字典,通过 update(dict) 进行更新。通过 add_meter(name, meter) 函数添加键值。
log_every(data_loader, print_freq, header) 打印一些中间结果。
总结:¶
本文介绍的是 Transformer 的基础,包含什么是 Attention,什么是 Transformer,以及在检测上的应用。其实在 DETR 之前已经有人尝试过把 self-attention 机制或者 Transformer 应用在视觉任务上面,但是关注不多。DETR 的出现使得这个模型开始广泛应用在各种视觉任务上面,我也会在这个专栏的后续多多解读这些经典工作。
参考文献:¶
- code:
https://github.com/jadore801120/attention-is-all-you-need-pytorchjadore801120/attention-is-all-you-need-pytorchhttps://github.com/jadore801120/attention-is-all-you-need-pytorchhttps://github.com/lucidrains/vit-pytorchhttps://github.com/facebookresearch/detrhttps://github.com/datawhalechina/leedeeprl-notes
- video:
第 1 小节的部分插图和文字稿来自李宏毅老师 PPT (如下链接) [侵删]。
https://www.bilibili.com/video/av71295187/?spm_id_from=333.788.videocard.8
- blog:
Transformer 模型详解深度眸:3W 字长文带你轻松入门视觉 transformer利用 python 解决指派问题(匈牙利算法)_your_answer 的博客 - CSDN 博客