5.2 Compositional analysis¶
Motivation¶
除了基因表达模式的变化，细胞成分（如细胞类型的比例）在不同条件下也可能发生变化。例如，某种特定药物可能会诱导细胞类型的转分化，这将在细胞身份组成中反映出来。为了准确确定细胞身份簇的比例和背景变化，需要足够的细胞和样本数量。可以在细胞身份簇的层面进行组成分析，这些簇可以是已知的细胞类型或对应于最近受到扰动影响的细胞状态。
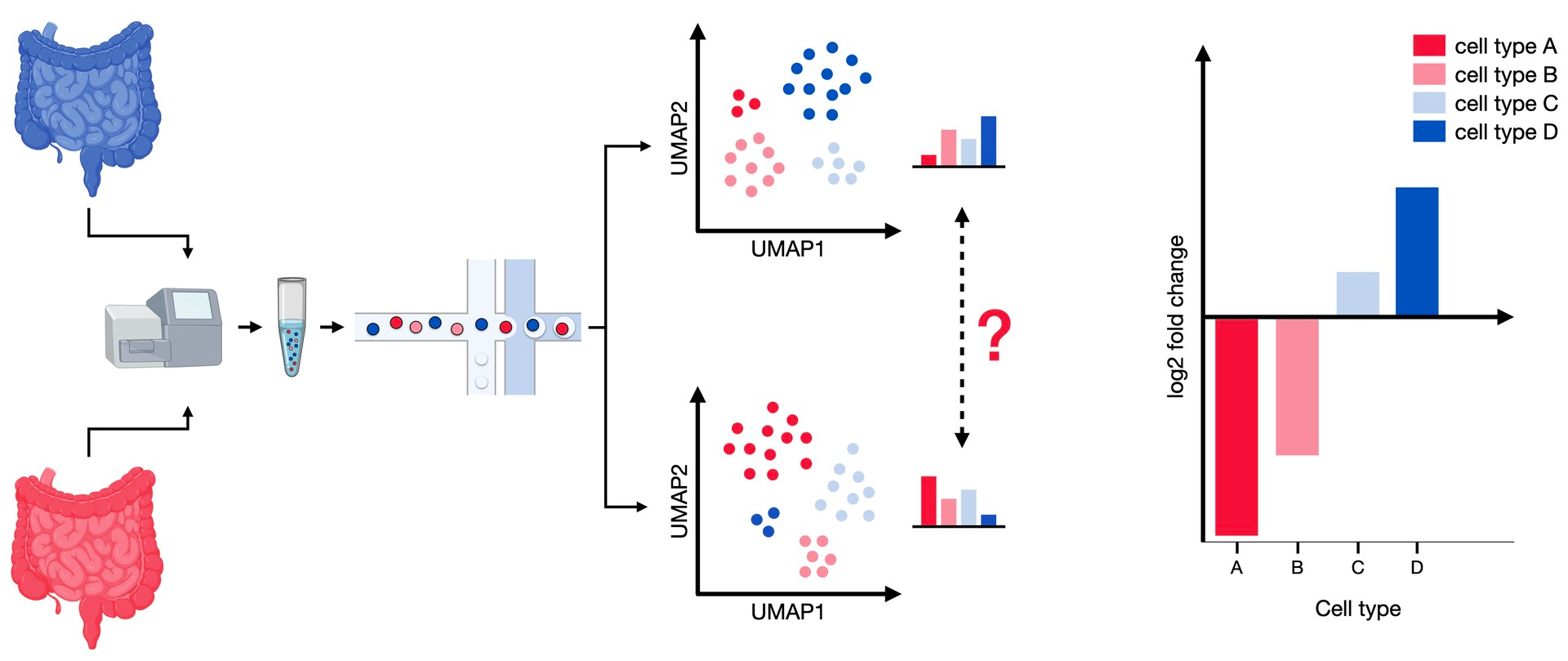
组成分析概述
差异丰度分析比较两种条件下细胞类型的组成。来自两种模式的样本包含不同比例的细胞类型，可以测试其丰度的显著变化。
本章将介绍这两种方法并将其应用于Haber数据集{cite}comp:Haber2017。该数据集包含来自小肠和小肠类器官的53,193个个体上皮细胞，其中一些细胞还受到细菌或蠕虫感染，例如沙门氏菌和多毛类蠕虫Heligmosomoides polygyrus感染。
在本教程中，我们使用了Haber数据集的一个子集，该子集仅包括专门为此目的收集的对照和感染细胞。值得注意的是，我们排除了一个仅收集大细胞的附加数据集，以便更快地计算和减少复杂性。
第一步，我们加载数据集。
Data loading¶
In [ ]:
Copied!
import warnings
import pandas as pd
warnings.filterwarnings("ignore")
warnings.simplefilter("ignore")
import scanpy as sc
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
import matplotlib
import seaborn as sns
import altair as alt
import pertpy as pt
import warnings
import pandas as pd
warnings.filterwarnings("ignore")
warnings.simplefilter("ignore")
import scanpy as sc
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
import matplotlib
import seaborn as sns
import altair as alt
import pertpy as pt
In [2]:
Copied!
adata = pt.dt.haber_2017_regions()
adata = pt.dt.haber_2017_regions()
In [3]:
Copied!
adata
adata
Out[3]:
AnnData object with n_obs × n_vars = 9842 × 15215
obs: 'batch', 'barcode', 'condition', 'cell_label'
In [4]:
Copied!
adata.obs
adata.obs
Out[4]:
| batch | barcode | condition | cell_label | |
|---|---|---|---|---|
| index | ||||
| B1_AAACATACCACAAC_Control_Enterocyte.Progenitor | B1 | AAACATACCACAAC | Control | Enterocyte.Progenitor |
| B1_AAACGCACGAGGAC_Control_Stem | B1 | AAACGCACGAGGAC | Control | Stem |
| B1_AAACGCACTAGCCA_Control_Stem | B1 | AAACGCACTAGCCA | Control | Stem |
| B1_AAACGCACTGTCCC_Control_Stem | B1 | AAACGCACTGTCCC | Control | Stem |
| B1_AAACTTGACCACCT_Control_Enterocyte.Progenitor | B1 | AAACTTGACCACCT | Control | Enterocyte.Progenitor |
| ... | ... | ... | ... | ... |
| B10_TTTCACGACAAGCT_Salmonella_TA | B10 | TTTCACGACAAGCT | Salmonella | TA |
| B10_TTTCAGTGAGGCGA_Salmonella_Enterocyte | B10 | TTTCAGTGAGGCGA | Salmonella | Enterocyte |
| B10_TTTCAGTGCGACAT_Salmonella_Stem | B10 | TTTCAGTGCGACAT | Salmonella | Stem |
| B10_TTTCAGTGTGACCA_Salmonella_Endocrine | B10 | TTTCAGTGTGACCA | Salmonella | Endocrine |
| B10_TTTCAGTGTTCTCA_Salmonella_Enterocyte.Progenitor | B10 | TTTCAGTGTTCTCA | Salmonella | Enterocyte.Progenitor |
9842 rows × 4 columns
数据分为10批收集。独特的条件包括对照组、沙门氏菌感染组、Hpoly.Day3和Hpoly.Day10，分别对应健康对照状态、沙门氏菌感染、Heligmosomoides polygyrus感染3天后的细胞以及Heligmosomoides polygyrus感染10天后的细胞。cell_label对应于细胞类型。
Why cell-type count data is compositional¶
在分析细胞计数数据的组成变化时，需要考虑多种技术和方法上的限制。一个挑战是实验重复样本数量较少，这导致在使用频率统计检验进行差异丰度分析时会产生较大的置信区间。
更重要的是，单细胞测序在每个样本中的细胞数量上具有自然限制——我们无法测序组织或器官中的每一个细胞，而是使用一个小的、具有代表性的快照。然而，这迫使我们将细胞类型计数视为纯粹的比例，即样本中的细胞总数仅是一个缩放因子。在统计学文献中，这种数据被称为组成数据{cite}Aitchison1982，其特征是在一个样本中所有特征（在我们的情况下是细胞类型）的相对丰度总和为1。
由于这种总和为1的限制，细胞类型丰度之间会产生负相关。为了说明这一点，我们考虑以下示例：
在一个病例对照研究中，我们希望比较健康和疾病状态下器官的细胞类型组成。在两种情况下，我们都有三种细胞类型（A、B和C），但它们的丰度不同：
- 健康器官由每种类型的2,000个细胞组成（共6,000个细胞）。
- 疾病导致细胞类型A的数量翻倍，而细胞类型B和C不受影响，因此患病器官有8,000个细胞。
In [5]:
Copied!
healthy_tissue = [2000, 2000, 2000]
diseased_tissue = [4000, 2000, 2000]
example_data_global = pd.DataFrame(
data=np.array([healthy_tissue, diseased_tissue]),
index=[1, 2],
columns=["A", "B", "C"],
)
example_data_global["Disease status"] = ["Healthy", "Diseased"]
example_data_global
healthy_tissue = [2000, 2000, 2000]
diseased_tissue = [4000, 2000, 2000]
example_data_global = pd.DataFrame(
data=np.array([healthy_tissue, diseased_tissue]),
index=[1, 2],
columns=["A", "B", "C"],
)
example_data_global["Disease status"] = ["Healthy", "Diseased"]
example_data_global
Out[5]:
| A | B | C | Disease status | |
|---|---|---|---|---|
| 1 | 2000 | 2000 | 2000 | Healthy |
| 2 | 4000 | 2000 | 2000 | Diseased |
In [6]:
Copied!
plot_data_global = example_data_global.melt(
"Disease status", ["A", "B", "C"], "Cell type", "count"
)
fig, ax = plt.subplots(1, 2, figsize=(12, 6))
sns.barplot(
data=plot_data_global, x="Disease status", y="count", hue="Cell type", ax=ax[0]
)
ax[0].set_title("Global abundances, by status")
sns.barplot(
data=plot_data_global, x="Cell type", y="count", hue="Disease status", ax=ax[1]
)
ax[1].set_title("Global abundances, by cell type")
plt.show()
plot_data_global = example_data_global.melt(
"Disease status", ["A", "B", "C"], "Cell type", "count"
)
fig, ax = plt.subplots(1, 2, figsize=(12, 6))
sns.barplot(
data=plot_data_global, x="Disease status", y="count", hue="Cell type", ax=ax[0]
)
ax[0].set_title("Global abundances, by status")
sns.barplot(
data=plot_data_global, x="Cell type", y="count", hue="Disease status", ax=ax[1]
)
ax[1].set_title("Global abundances, by cell type")
plt.show()
我们想找出在患病器官中哪些细胞类型的丰度增加或减少。如果我们能够确定两个器官中每个细胞的类型，情况将很清楚，如上图右侧所示。不幸的是，这是不可能的。由于我们的测序过程能力有限，我们只能从两个群体中取600个细胞的代表性样本。为了模拟这一步，我们可以使用numpy的random.multinomial函数从群体中不放回地抽取600个细胞：
In [7]:
Copied!
np.random.seed(1234)
healthy_sample = np.random.multinomial(
pvals=healthy_tissue / np.sum(healthy_tissue), n=600
)
diseased_sample = np.random.multinomial(
pvals=diseased_tissue / np.sum(diseased_tissue), n=600
)
example_data_sample = pd.DataFrame(
data=np.array([healthy_sample, diseased_sample]),
index=[1, 2],
columns=["A", "B", "C"],
)
example_data_sample["Disease status"] = ["Healthy", "Diseased"]
example_data_sample
np.random.seed(1234)
healthy_sample = np.random.multinomial(
pvals=healthy_tissue / np.sum(healthy_tissue), n=600
)
diseased_sample = np.random.multinomial(
pvals=diseased_tissue / np.sum(diseased_tissue), n=600
)
example_data_sample = pd.DataFrame(
data=np.array([healthy_sample, diseased_sample]),
index=[1, 2],
columns=["A", "B", "C"],
)
example_data_sample["Disease status"] = ["Healthy", "Diseased"]
example_data_sample
Out[7]:
| A | B | C | Disease status | |
|---|---|---|---|---|
| 1 | 193 | 201 | 206 | Healthy |
| 2 | 296 | 146 | 158 | Diseased |
In [8]:
Copied!
plot_data_sample = example_data_sample.melt(
"Disease status", ["A", "B", "C"], "Cell type", "count"
)
fig, ax = plt.subplots(1, 2, figsize=(12, 6))
sns.barplot(
data=plot_data_sample, x="Disease status", y="count", hue="Cell type", ax=ax[0]
)
ax[0].set_title("Sampled abundances, by status")
sns.barplot(
data=plot_data_sample, x="Cell type", y="count", hue="Disease status", ax=ax[1]
)
ax[1].set_title("Sampled abundances, by cell type")
plt.show()
plot_data_sample = example_data_sample.melt(
"Disease status", ["A", "B", "C"], "Cell type", "count"
)
fig, ax = plt.subplots(1, 2, figsize=(12, 6))
sns.barplot(
data=plot_data_sample, x="Disease status", y="count", hue="Cell type", ax=ax[0]
)
ax[0].set_title("Sampled abundances, by status")
sns.barplot(
data=plot_data_sample, x="Cell type", y="count", hue="Disease status", ax=ax[1]
)
ax[1].set_title("Sampled abundances, by cell type")
plt.show()
现在情况变得不再清晰。虽然细胞类型A的计数仍然增加（大约从200增加到300），但其他两种细胞类型似乎从大约200减少到150。这种明显的减少是由于我们限制在600个细胞的样本中——如果样本中更大比例被细胞类型A占据，那么细胞类型B和C的份额必须减少。因此，在不考虑其他细胞类型的情况下，确定一种细胞类型的丰度变化是不可能的。
如果我们忽略数据的组成特性，使用Wilcoxon秩和检验或scDC等单变量方法（后者通过bootstrap重采样进行差异细胞类型组成分析{cite}comp:Cao2019），我们可能会错误地将细胞类型群体变化视为统计显著的效果，尽管它们是由细胞类型比例的固有负相关引起的。
此外，子样本数据不仅为我们的问题提供一个有效的解决方案。如果在患病情况下，细胞类型B和C都减少了1,000个细胞，我们将获得与上述相同的600个细胞的代表性样本。为了获得唯一的结果，我们可以为数据确定一个参考点，假设在所有样本中保持不变{cite}Brill2019。这可以是单一细胞类型、多个细胞类型的几何平均数聚合，或者一组正交基{cite}Egozcue2003。
虽然足够大的单细胞数据集和重复样本数仅在近年来出现，但相同的统计特性也在微生物分析中被讨论{cite}Gloor2017。在这种情况下，一些流行的方法包括ANCOM-BC{cite}Lin2020和ALDEx2{cite}Fernandes2014。然而，这些方法由于实验重复样本数量少，往往在单细胞数据集中遇到困难。
这个问题已经被scCODA{cite}Büttner2021解决了，我们将在接下来的部分介绍并将其应用于我们的数据集。
With labeled clusters¶
scCODA 属于需要预定义簇（最常见的是细胞类型）的一类工具，通过统计方法推导组成变化。受微生物群数据组成分析方法的启发，scCODA提出了一种贝叶斯方法，以解决单细胞分析中常见的低重复问题{cite}Büttner2021。它使用层次狄利克雷-多项式模型对细胞类型计数进行建模，通过联合建模所有测量的细胞类型比例来考虑细胞类型比例的不确定性和负相关偏差。为了确保解决方案的唯一可识别性和易于解释，scCODA选择特定的细胞类型作为参考。因此，scCODA检测到的任何组成变化都必须相对于所选择的参考细胞类型来看。
然而，scCODA假设协变量和细胞丰度之间存在对数线性关系，在使用连续协变量时，这可能并不总能反映潜在的生物过程。scCODA的另一个限制是无法推断超越组成效应的细胞组成之间的相关结构。此外，scCODA仅对均值丰度的变化进行建模，但无法检测响应变化中的变异性{cite}Büttner2021。
第一步，我们实例化一个scCODA模型。
然后，我们使用load函数来准备一个MuData对象以进行后续处理，并从输入的adata创建一个组成分析数据集。在我们的情况下，我们将cell_type_identifier指定为cell_label，sample_identifier指定为batch，并将covariate_obs指定为condition。
In [9]:
Copied!
sccoda_model = pt.tl.Sccoda()
sccoda_data = sccoda_model.load(
adata,
type="cell_level",
generate_sample_level=True,
cell_type_identifier="cell_label",
sample_identifier="batch",
covariate_obs=["condition"],
)
sccoda_data
sccoda_model = pt.tl.Sccoda()
sccoda_data = sccoda_model.load(
adata,
type="cell_level",
generate_sample_level=True,
cell_type_identifier="cell_label",
sample_identifier="batch",
covariate_obs=["condition"],
)
sccoda_data
Out[9]:
MuData object with n_obs × n_vars = 9852 × 15223
2 modalities
rna: 9842 x 15215
obs: 'batch', 'barcode', 'condition', 'cell_label', 'scCODA_sample_id'
coda: 10 x 8
obs: 'condition', 'batch'
var: 'n_cells'
为了概览不同条件下的细胞类型分布，我们可以使用scCODA的boxplots。为了更好地理解数据的分布，红点表示实际的数据点。
In [10]:
Copied!
pt.pl.coda.boxplots(
sccoda_data,
modality_key="coda",
feature_name="condition",
figsize=(12, 5),
add_dots=True,
args_swarmplot={"palette": ["red"]},
)
plt.show()
pt.pl.coda.boxplots(
sccoda_data,
modality_key="coda",
feature_name="condition",
figsize=(12, 5),
add_dots=True,
args_swarmplot={"palette": ["red"]},
)
plt.show()
箱线图突出显示了细胞类型分布中的一些差异。显著的是沙门氏菌条件下高比例的肠上皮细胞。但其他细胞类型，如转运扩增（TA）细胞，在沙门氏菌条件下与对照相比也显示出显著的丰度差异。这些差异是否具有统计显著性需要进行适当的评估。
一种替代的可视化方式是scCODA提供的堆叠条形图。这种可视化很好地展示了组成数据的特性：如果我们比较对照组和沙门氏菌组，可以看到感染小鼠中肠上皮细胞的比例显著增加。由于数据是成比例的，这导致其他所有细胞类型的比例减少，以满足总和为一的限制。
In [11]:
Copied!
pt.pl.coda.stacked_barplot(
sccoda_data, modality_key="coda", feature_name="condition", figsize=(4, 2)
)
plt.show()
pt.pl.coda.stacked_barplot(
sccoda_data, modality_key="coda", feature_name="condition", figsize=(4, 2)
)
plt.show()
scCODA需要两个主要参数，除了细胞计数的AnnData对象：一个公式和一个参考细胞类型。公式描述了协变量，使用R-style指定。在我们的例子中，我们将条件指定为唯一的协变量。由于它是具有四个级别（对照和三种疾病状态）的离散协变量，这种建模方式比较了每个状态与其他样本的比较。
如果我们想一次建模多个协变量，只需在公式中添加它们（即formula = "covariate_1 + covariate_2"）即可。如前所述，scCODA需要一个参考细胞类型进行比较，该细胞类型被认为不会受到协变量的影响。scCODA可以自动选择一个适当的细胞类型作为参考，即在所有样本中相对丰度几乎恒定的细胞类型，也可以使用用户指定的参考细胞类型。这里我们将内分泌细胞设置为参考，因为从视觉上看，它们的丰度似乎相当恒定。另一种设置参考细胞类型的方法是将reference_cell_type设置为"automatic"，这将强制scCODA自行选择一个合适的参考细胞类型。如果参考细胞类型的选择不明确，我们建议使用此选项来获得一个指示甚至最终选择。
In [12]:
Copied!
sccoda_data = sccoda_model.prepare(
sccoda_data,
modality_key="coda",
formula="condition",
reference_cell_type="Endocrine",
)
sccoda_model.run_nuts(sccoda_data, modality_key="coda", rng_key=1234)
sccoda_data = sccoda_model.prepare(
sccoda_data,
modality_key="coda",
formula="condition",
reference_cell_type="Endocrine",
)
sccoda_model.run_nuts(sccoda_data, modality_key="coda", rng_key=1234)
sample: 100%|██████████| 11000/11000 [01:08<00:00, 161.54it/s, 255 steps of size 1.72e-02. acc. prob=0.85]
In [13]:
Copied!
sccoda_data["coda"].varm["effect_df_condition[T.Salmonella]"]
sccoda_data["coda"].varm["effect_df_condition[T.Salmonella]"]
Out[13]:
| Final Parameter | HDI 3% | HDI 97% | SD | Inclusion probability | Expected Sample | log2-fold change | |
|---|---|---|---|---|---|---|---|
| Cell Type | |||||||
| Endocrine | 0.0000 | 0.000 | 0.000 | 0.000 | 0.0000 | 32.598994 | -0.526812 |
| Enterocyte | 1.5458 | 0.985 | 2.071 | 0.283 | 0.9996 | 382.634978 | 1.703306 |
| Enterocyte.Progenitor | 0.0000 | -0.475 | 0.566 | 0.143 | 0.2817 | 126.126003 | -0.526812 |
| Goblet | 0.0000 | -0.345 | 1.013 | 0.290 | 0.4354 | 52.735108 | -0.526812 |
| Stem | 0.0000 | -0.742 | 0.297 | 0.173 | 0.3092 | 135.406509 | -0.526812 |
| TA | 0.0000 | -0.876 | 0.331 | 0.211 | 0.3358 | 78.986854 | -0.526812 |
| TA.Early | 0.0000 | -0.338 | 0.615 | 0.151 | 0.3033 | 152.670412 | -0.526812 |
| Tuft | 0.0000 | -1.221 | 0.548 | 0.342 | 0.4098 | 23.041143 | -0.526812 |
接受率描述了初始预热阶段后被接受的提议样本的比例，可以作为优化运行不良的临时指示器。在scCODA的情况下，理想的接受率在0.4到0.9之间。接受率过高或过低表明采样过程存在问题。
In [14]:
Copied!
sccoda_data
sccoda_data
Out[14]:
MuData object with n_obs × n_vars = 9852 × 15223
2 modalities
rna: 9842 x 15215
obs: 'batch', 'barcode', 'condition', 'cell_label', 'scCODA_sample_id'
coda: 10 x 8
obs: 'condition', 'batch'
var: 'n_cells'
uns: 'scCODA_params'
obsm: 'covariate_matrix', 'sample_counts'
varm: 'intercept_df', 'effect_df_condition[T.Hpoly.Day3]', 'effect_df_condition[T.Hpoly.Day10]', 'effect_df_condition[T.Salmonella]'
scCODA基于包含概率选择可信效应。可信效应和非可信效应之间的界限取决于所需的假发现率（FDR）。较小的FDR值会产生更保守的结果，但可能会错过一些效应，而较大的FDR值会选择更多效应，但会增加假发现的数量。
所需的FDR水平可以在推断后通过sim_results.set_fdr()轻松设置。默认值为0.05。由于FDR可以对结果产生重大影响，建议尝试不同的FDR值，最高可达0.2，以获得最显著的效应。
在我们的案例中，我们使用较宽松的FDR值0.2。
In [15]:
Copied!
sccoda_model.set_fdr(sccoda_data, 0.2)
sccoda_model.set_fdr(sccoda_data, 0.2)
为了获得每种细胞类型的组成变化的二元分类，我们使用scCODA在结果对象上的credible_effects函数。每个标记为"True"的细胞类型在统计上有显著的增加或减少。折叠变化（fold-changes）描述了细胞类型是增加还是减少。因此，我们将它们与二元分类一起绘制。
In [16]:
Copied!
sccoda_model.credible_effects(sccoda_data, modality_key="coda")
sccoda_model.credible_effects(sccoda_data, modality_key="coda")
Out[16]:
Covariate Cell Type
condition[T.Hpoly.Day3] Endocrine False
Enterocyte False
Enterocyte.Progenitor False
Goblet False
Stem False
TA False
TA.Early False
Tuft False
condition[T.Hpoly.Day10] Endocrine False
Enterocyte True
Enterocyte.Progenitor False
Goblet False
Stem False
TA False
TA.Early False
Tuft True
condition[T.Salmonella] Endocrine False
Enterocyte True
Enterocyte.Progenitor False
Goblet False
Stem False
TA False
TA.Early False
Tuft False
Name: Final Parameter, dtype: bool
To plot the fold changes together with the binary classification, we can easily use effects_bar_plot function.
In [17]:
Copied!
pt.pl.coda.effects_barplot(sccoda_data, "coda", "condition")
plt.show()
pt.pl.coda.effects_barplot(sccoda_data, "coda", "condition")
plt.show()
这些图很好地展示了条件对细胞类型的显著和可信效应。这些效应大体上与Haber论文中的发现一致，该论文使用了非组成的泊松回归模型来进行分析：
- "在沙门氏菌感染后，成熟肠上皮细胞的频率显著增加。" {cite}
comp:Haber2017 - "Heligmosomoides polygyrus导致杯状细胞和簇状细胞的丰度增加。" {cite}
comp:Haber2017
熟悉原始出版物的读者可能会想知道为什么Haber等人使用的模型发现了比scCODA更多的显著效应，例如在沙门氏菌感染的情况下，干细胞和转运扩增细胞的减少 {cite}comp:Haber2017。为了解释这种差异，请记住细胞计数数据是组成数据，因此一种细胞类型相对丰度的增加将导致所有其他细胞类型相对丰度的减少。
由于沙门氏菌感染小鼠小肠上皮中肠上皮细胞的显著增加，所有其他细胞类型似乎都减少了，即使这种变化仅由数据的组成特性引起。虽然原始（单变量）泊松回归模型会捕捉到这些可能的假阳性效应，但scCODA能够考虑数据的组成性，因此不会陷入这个陷阱。
With labeled clusters and hierarchical structure¶
除了每种细胞类型的丰度外，典型的单细胞数据集还包含关于不同细胞相似性的信息，以树状层次排序的形式表示。这些层次结构可以通过基因表达的聚类自动确定（通常用于发现属于同一细胞类型的细胞簇），也可以通过生物学信息指导的层次结构如细胞谱系来确定。
tascCODA 是scCODA的扩展，它将层次信息和实验协变量数据集成到组成计数数据的生成模型中{cite}Ostner2021。这对于分辨率提高的细胞图谱工作特别有益。
它的核心几乎使用了与scCODA相同的Dirichlet-多项式设置，但扩展了模型，以便在树结构中的内部节点上定义的细胞类型集合上施加效应。
In [18]:
Copied!
import schist
warnings.filterwarnings("ignore")
warnings.simplefilter("ignore")
import schist
warnings.filterwarnings("ignore")
warnings.simplefilter("ignore")
objc[13344]: Class GNotificationCenterDelegate is implemented in both /opt/anaconda3/lib/libgio-2.0.0.dylib (0x18ef5ec30) and /usr/local/Cellar/glib/2.74.4/lib/libgio-2.0.0.dylib (0x19be736b0). One of the two will be used. Which one is undefined.
为了使用tascCODA，我们首先需要定义细胞类型的层次排序。一种可能的层次聚类方法是使用八种细胞类型，并通过它们在PCA表示中的相似性（皮尔逊相关性）进行排序，使用sc.tl.dendrogram。
由于在我们的数据中这种结构非常简单，因此不会给我们带来很多新的见解，我们希望有一个更复杂的聚类。最近的一种方法是使用schist包{cite}Morelli2021，该方法使用嵌套随机块模型，在不同分辨率级别上对细胞群体进行聚类。使用标准设置运行此方法需要一些时间（在我们的数据上大约需要15分钟），并为我们提供每个细胞在adata.obs中的层次聚类分配。
首先，我们需要通过PCA嵌入定义细胞之间的距离度量：
In [19]:
Copied!
# use logcounts to calculate PCA and neighbors
adata.layers["counts"] = adata.X.copy()
adata.layers["logcounts"] = sc.pp.log1p(adata.layers["counts"]).copy()
adata.X = adata.layers["logcounts"].copy()
sc.pp.neighbors(adata, n_neighbors=10, n_pcs=30, random_state=1234)
# Calculate UMAP for visualization purposes
sc.tl.umap(adata)
# use logcounts to calculate PCA and neighbors
adata.layers["counts"] = adata.X.copy()
adata.layers["logcounts"] = sc.pp.log1p(adata.layers["counts"]).copy()
adata.X = adata.layers["logcounts"].copy()
sc.pp.neighbors(adata, n_neighbors=10, n_pcs=30, random_state=1234)
# Calculate UMAP for visualization purposes
sc.tl.umap(adata)
WARNING: You’re trying to run this on 15215 dimensions of `.X`, if you really want this, set `use_rep='X'`.
Falling back to preprocessing with `sc.pp.pca` and default params.
Then, we can run schist on the AnnData object, which results in a clustering that is defined through a set of columns "nsbm_level_{i}" in adata.obs:
In [20]:
Copied!
schist.inference.nested_model(adata, samples=100, random_seed=5678)
adata.obs
schist.inference.nested_model(adata, samples=100, random_seed=5678)
adata.obs
objc[13409]: Class GNotificationCenterDelegate is implemented in both /opt/anaconda3/lib/libgio-2.0.0.dylib (0x12f0f1c30) and /usr/local/Cellar/glib/2.74.4/lib/libgio-2.0.0.dylib (0x1448ce6b0). One of the two will be used. Which one is undefined. objc[13410]: Class GNotificationCenterDelegate is implemented in both /opt/anaconda3/lib/libgio-2.0.0.dylib (0x1265f3c30) and /usr/local/Cellar/glib/2.74.4/lib/libgio-2.0.0.dylib (0x13bdb76b0). One of the two will be used. Which one is undefined. objc[13408]: Class GNotificationCenterDelegate is implemented in both /opt/anaconda3/lib/libgio-2.0.0.dylib (0x125a9ec30) and /usr/local/Cellar/glib/2.74.4/lib/libgio-2.0.0.dylib (0x13b1576b0). One of the two will be used. Which one is undefined. objc[13411]: Class GNotificationCenterDelegate is implemented in both /opt/anaconda3/lib/libgio-2.0.0.dylib (0x129969c30) and /usr/local/Cellar/glib/2.74.4/lib/libgio-2.0.0.dylib (0x13f0d36b0). One of the two will be used. Which one is undefined. objc[13407]: Class GNotificationCenterDelegate is implemented in both /opt/anaconda3/lib/libgio-2.0.0.dylib (0x127cb9c30) and /usr/local/Cellar/glib/2.74.4/lib/libgio-2.0.0.dylib (0x13d4106b0). One of the two will be used. Which one is undefined. objc[13414]: Class GNotificationCenterDelegate is implemented in both /opt/anaconda3/lib/libgio-2.0.0.dylib (0x12ee9ac30) and /usr/local/Cellar/glib/2.74.4/lib/libgio-2.0.0.dylib (0x1446806b0). One of the two will be used. Which one is undefined. Numba: Attempted to fork from a non-main thread, the TBB library may be in an invalid state in the child process. Numba: Attempted to fork from a non-main thread, the TBB library may be in an invalid state in the child process. objc[13490]: Class GNotificationCenterDelegate is implemented in both /opt/anaconda3/lib/libgio-2.0.0.dylib (0x124cf9c30) and /usr/local/Cellar/glib/2.74.4/lib/libgio-2.0.0.dylib (0x13a4136b0). One of the two will be used. Which one is undefined. objc[13492]: Class GNotificationCenterDelegate is implemented in both /opt/anaconda3/lib/libgio-2.0.0.dylib (0x131710c30) and /usr/local/Cellar/glib/2.74.4/lib/libgio-2.0.0.dylib (0x146e806b0). One of the two will be used. Which one is undefined. Numba: Attempted to fork from a non-main thread, the TBB library may be in an invalid state in the child process. objc[13660]: Class GNotificationCenterDelegate is implemented in both /opt/anaconda3/lib/libgio-2.0.0.dylib (0x13455ec30) and /usr/local/Cellar/glib/2.74.4/lib/libgio-2.0.0.dylib (0x149c2f6b0). One of the two will be used. Which one is undefined. Numba: Attempted to fork from a non-main thread, the TBB library may be in an invalid state in the child process. objc[13699]: Class GNotificationCenterDelegate is implemented in both /opt/anaconda3/lib/libgio-2.0.0.dylib (0x131764c30) and /usr/local/Cellar/glib/2.74.4/lib/libgio-2.0.0.dylib (0x146ee86b0). One of the two will be used. Which one is undefined. Numba: Attempted to fork from a non-main thread, the TBB library may be in an invalid state in the child process. objc[13757]: Class GNotificationCenterDelegate is implemented in both /opt/anaconda3/lib/libgio-2.0.0.dylib (0x12ad09c30) and /usr/local/Cellar/glib/2.74.4/lib/libgio-2.0.0.dylib (0x1404af6b0). One of the two will be used. Which one is undefined. Numba: Attempted to fork from a non-main thread, the TBB library may be in an invalid state in the child process. objc[14239]: Class GNotificationCenterDelegate is implemented in both /opt/anaconda3/lib/libgio-2.0.0.dylib (0x1278c5c30) and /usr/local/Cellar/glib/2.74.4/lib/libgio-2.0.0.dylib (0x13d0326b0). One of the two will be used. Which one is undefined. Numba: Attempted to fork from a non-main thread, the TBB library may be in an invalid state in the child process. objc[14327]: Class GNotificationCenterDelegate is implemented in both /opt/anaconda3/lib/libgio-2.0.0.dylib (0x132a2ec30) and /usr/local/Cellar/glib/2.74.4/lib/libgio-2.0.0.dylib (0x1481d76b0). One of the two will be used. Which one is undefined. Numba: Attempted to fork from a non-main thread, the TBB library may be in an invalid state in the child process. Numba: Attempted to fork from a non-main thread, the TBB library may be in an invalid state in the child process. objc[14348]: Class GNotificationCenterDelegate is implemented in both /opt/anaconda3/lib/libgio-2.0.0.dylib (0x1343f7c30) and /usr/local/Cellar/glib/2.74.4/lib/libgio-2.0.0.dylib (0x149ba86b0). One of the two will be used. Which one is undefined. objc[14356]: Class GNotificationCenterDelegate is implemented in both /opt/anaconda3/lib/libgio-2.0.0.dylib (0x12f11cc30) and /usr/local/Cellar/glib/2.74.4/lib/libgio-2.0.0.dylib (0x1448ce6b0). One of the two will be used. Which one is undefined.
Out[20]:
| batch | barcode | condition | cell_label | scCODA_sample_id | nsbm_level_0 | nsbm_level_1 | nsbm_level_2 | nsbm_level_3 | nsbm_level_4 | nsbm_level_5 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| index | |||||||||||
| B1_AAACATACCACAAC_Control_Enterocyte.Progenitor | B1 | AAACATACCACAAC | Control | Enterocyte.Progenitor | B1 | 0 | 0 | 0 | 0 | 0 | 0 |
| B1_AAACGCACGAGGAC_Control_Stem | B1 | AAACGCACGAGGAC | Control | Stem | B1 | 1 | 5 | 3 | 1 | 0 | 0 |
| B1_AAACGCACTAGCCA_Control_Stem | B1 | AAACGCACTAGCCA | Control | Stem | B1 | 10 | 2 | 2 | 1 | 0 | 0 |
| B1_AAACGCACTGTCCC_Control_Stem | B1 | AAACGCACTGTCCC | Control | Stem | B1 | 34 | 3 | 3 | 1 | 0 | 0 |
| B1_AAACTTGACCACCT_Control_Enterocyte.Progenitor | B1 | AAACTTGACCACCT | Control | Enterocyte.Progenitor | B1 | 91 | 35 | 0 | 0 | 0 | 0 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| B10_TTTCACGACAAGCT_Salmonella_TA | B10 | TTTCACGACAAGCT | Salmonella | TA | B10 | 6 | 5 | 3 | 1 | 0 | 0 |
| B10_TTTCAGTGAGGCGA_Salmonella_Enterocyte | B10 | TTTCAGTGAGGCGA | Salmonella | Enterocyte | B10 | 142 | 36 | 4 | 1 | 0 | 0 |
| B10_TTTCAGTGCGACAT_Salmonella_Stem | B10 | TTTCAGTGCGACAT | Salmonella | Stem | B10 | 112 | 1 | 1 | 1 | 0 | 0 |
| B10_TTTCAGTGTGACCA_Salmonella_Endocrine | B10 | TTTCAGTGTGACCA | Salmonella | Endocrine | B10 | 146 | 36 | 4 | 1 | 0 | 0 |
| B10_TTTCAGTGTTCTCA_Salmonella_Enterocyte.Progenitor | B10 | TTTCAGTGTTCTCA | Salmonella | Enterocyte.Progenitor | B10 | 77 | 14 | 6 | 3 | 0 | 0 |
9842 rows × 11 columns
UMAP图很好地展示了schist的聚类（在这里是层次1和层次2）与细胞类型分配的关联。层次1的表示是上一级别的严格细化，即每个层次2的簇被分成多个更小的簇：
In [21]:
Copied!
sc.pl.umap(
adata, color=["nsbm_level_1", "nsbm_level_2", "cell_label"], ncols=3, wspace=0.5
)
sc.pl.umap(
adata, color=["nsbm_level_1", "nsbm_level_2", "cell_label"], ncols=3, wspace=0.5
)
现在，我们将细胞级数据转换为样本级数据并创建树结构。我们创建一个tasccoda_model对象，方法与scCODA相同，但使用由schist定义的聚类和树级别。
Tasccoda的load函数将准备一个MuData对象，并将我们的树表示转换为一个ete树结构，并将其保存为tasccoda_data['coda'].uns["tree"]。为了得到一些不过小的聚类，我们在最后一级之前切割树结构，省略"nsbm_level_0"。
In [22]:
Copied!
tasccoda_model = pt.tl.Tasccoda()
tasccoda_data = tasccoda_model.load(
adata,
type="cell_level",
cell_type_identifier="nsbm_level_1",
sample_identifier="batch",
covariate_obs=["condition"],
levels_orig=["nsbm_level_4", "nsbm_level_3", "nsbm_level_2", "nsbm_level_1"],
add_level_name=True,
)
tasccoda_data
tasccoda_model = pt.tl.Tasccoda()
tasccoda_data = tasccoda_model.load(
adata,
type="cell_level",
cell_type_identifier="nsbm_level_1",
sample_identifier="batch",
covariate_obs=["condition"],
levels_orig=["nsbm_level_4", "nsbm_level_3", "nsbm_level_2", "nsbm_level_1"],
add_level_name=True,
)
tasccoda_data
Out[22]:
MuData object with n_obs × n_vars = 9852 × 15256
2 modalities
rna: 9842 x 15215
obs: 'batch', 'barcode', 'condition', 'cell_label', 'scCODA_sample_id', 'nsbm_level_0', 'nsbm_level_1', 'nsbm_level_2', 'nsbm_level_3', 'nsbm_level_4', 'nsbm_level_5'
uns: 'neighbors', 'umap', 'schist', 'nsbm_level_1_colors', 'nsbm_level_2_colors', 'cell_label_colors'
obsm: 'X_pca', 'X_umap', 'CM_nsbm_level_0', 'CM_nsbm_level_1', 'CM_nsbm_level_2', 'CM_nsbm_level_3', 'CM_nsbm_level_4', 'CM_nsbm_level_5'
layers: 'counts', 'logcounts'
obsp: 'distances', 'connectivities'
coda: 10 x 41
obs: 'condition', 'batch'
var: 'n_cells'
uns: 'tree'
In [23]:
Copied!
pt.pl.coda.draw_tree(tasccoda_data)
pt.pl.coda.draw_tree(tasccoda_data)
Out[23]:
tascCODA的模型设置和执行与scCODA类似，自由参数reference和formula也相同。此外，我们可以通过pen_args参数中的phi和lambda_1调整树聚合和模型选择（详情见{cite}Ostner2021）。在这里，我们使用无偏设置phi=0和比默认值稍微宽松的模型选择lambda_1=1.7。我们使用簇18作为参考，因为它几乎与内分泌细胞相同。
In [24]:
Copied!
tasccoda_model.prepare(
tasccoda_data,
modality_key="coda",
reference_cell_type="18",
formula="condition",
pen_args={"phi": 0, "lambda_1": 3.5},
tree_key="tree",
)
tasccoda_model.prepare(
tasccoda_data,
modality_key="coda",
reference_cell_type="18",
formula="condition",
pen_args={"phi": 0, "lambda_1": 3.5},
tree_key="tree",
)
Zero counts encountered in data! Added a pseudocount of 0.5.
Out[24]:
MuData object with n_obs × n_vars = 9852 × 15256
2 modalities
rna: 9842 x 15215
obs: 'batch', 'barcode', 'condition', 'cell_label', 'scCODA_sample_id', 'nsbm_level_0', 'nsbm_level_1', 'nsbm_level_2', 'nsbm_level_3', 'nsbm_level_4', 'nsbm_level_5'
uns: 'neighbors', 'umap', 'schist', 'nsbm_level_1_colors', 'nsbm_level_2_colors', 'cell_label_colors'
obsm: 'X_pca', 'X_umap', 'CM_nsbm_level_0', 'CM_nsbm_level_1', 'CM_nsbm_level_2', 'CM_nsbm_level_3', 'CM_nsbm_level_4', 'CM_nsbm_level_5'
layers: 'counts', 'logcounts'
obsp: 'distances', 'connectivities'
coda: 10 x 41
obs: 'condition', 'batch'
var: 'n_cells'
uns: 'tree', 'scCODA_params'
obsm: 'covariate_matrix', 'sample_counts'
In [25]:
Copied!
tasccoda_model.run_nuts(
tasccoda_data, modality_key="coda", rng_key=1234, num_samples=10000, num_warmup=1000
)
tasccoda_model.run_nuts(
tasccoda_data, modality_key="coda", rng_key=1234, num_samples=10000, num_warmup=1000
)
sample: 100%|██████████| 11000/11000 [04:50<00:00, 37.83it/s, 127 steps of size 3.18e-02. acc. prob=0.97]
In [26]:
Copied!
tasccoda_model.summary(tasccoda_data, modality_key="coda")
tasccoda_model.summary(tasccoda_data, modality_key="coda")
Compositional Analysis summary ┌────────────────────────────────────────────┬────────────────────────────────────────────────────────────────────┐ │ Name │ Value │ ├────────────────────────────────────────────┼────────────────────────────────────────────────────────────────────┤ │ Data │ Data: 10 samples, 41 cell types │ │ Reference cell type │ 18 │ │ Formula │ condition │ └────────────────────────────────────────────┴────────────────────────────────────────────────────────────────────┘
┌─────────────────────────────────────────────────────────────────────────────────────────────────────────────────┐ │ Intercepts │ ├─────────────────────────────────────────────────────────────────────────────────────────────────────────────────┤ │ Final Parameter Expected Sample │ │ Cell Type │ │ 0 1.313 53.195 │ │ 1 1.098 42.904 │ │ 2 1.205 47.749 │ │ 3 0.526 24.215 │ │ 4 -0.707 7.057 │ │ 5 0.634 26.976 │ │ 6 -0.432 9.290 │ │ 7 1.038 40.405 │ │ 8 1.276 51.263 │ │ 9 1.345 54.925 │ │ 10 0.625 26.735 │ │ 11 0.817 32.394 │ │ 12 -0.359 9.994 │ │ 13 0.260 18.559 │ │ 14 0.851 33.514 │ │ 15 0.524 24.166 │ │ 16 0.934 36.414 │ │ 17 -0.142 12.416 │ │ 18 0.684 28.360 │ │ 19 0.857 33.716 │ │ 20 0.198 17.443 │ │ 21 0.209 17.636 │ │ 22 -0.159 12.206 │ │ 23 0.913 35.658 │ │ 24 1.190 47.038 │ │ 25 0.057 15.149 │ │ 26 -0.086 13.131 │ │ 27 -0.002 14.281 │ │ 28 0.786 31.405 │ │ 29 -0.589 7.940 │ │ 30 -0.713 7.014 │ │ 31 0.210 17.654 │ │ 32 -0.797 6.449 │ │ 33 -0.806 6.391 │ │ 34 -0.839 6.184 │ │ 35 -0.104 12.897 │ │ 36 1.443 60.580 │ │ 37 0.215 17.742 │ │ 38 -1.062 4.948 │ │ 39 -0.879 5.942 │ │ 40 0.084 15.564 │ └─────────────────────────────────────────────────────────────────────────────────────────────────────────────────┘
┌─────────────────────────────────────────────────────────────────────────────────────────────────────────────────┐ │ Effects │ ├─────────────────────────────────────────────────────────────────────────────────────────────────────────────────┤ │ Effect Expected Sample log2-fold change │ │ Covariate Cell Type │ │ conditionT.Hpoly.Day3 0 0.000 51.027 -0.060 │ │ 1 0.000 41.155 -0.060 │ │ 2 -0.257 35.423 -0.431 │ │ 3 0.439 36.030 0.573 │ │ 4 0.000 6.769 -0.060 │ │ 5 0.439 40.139 0.573 │ │ 6 0.000 8.912 -0.060 │ │ 7 0.000 38.759 -0.060 │ │ 8 0.439 76.276 0.573 │ │ 9 -0.257 40.746 -0.431 │ │ 10 0.000 25.645 -0.060 │ │ 11 0.000 31.073 -0.060 │ │ 12 0.000 9.586 -0.060 │ │ 13 0.000 17.803 -0.060 │ │ 14 0.000 32.148 -0.060 │ │ 15 0.000 23.181 -0.060 │ │ 16 0.000 34.930 -0.060 │ │ 17 0.000 11.910 -0.060 │ │ 18 0.000 27.204 -0.060 │ │ 19 0.000 32.342 -0.060 │ │ 20 0.000 16.733 -0.060 │ │ 21 0.439 26.242 0.573 │ │ 22 0.000 11.709 -0.060 │ │ 23 -0.257 26.453 -0.431 │ │ 24 0.000 45.121 -0.060 │ │ 25 0.000 14.532 -0.060 │ │ 26 0.000 12.596 -0.060 │ │ 27 0.000 13.699 -0.060 │ │ 28 0.000 30.125 -0.060 │ │ 29 0.000 7.617 -0.060 │ │ 30 0.000 6.729 -0.060 │ │ 31 0.000 16.935 -0.060 │ │ 32 -0.257 4.784 -0.431 │ │ 33 0.000 6.131 -0.060 │ │ 34 0.000 5.932 -0.060 │ │ 35 0.000 12.371 -0.060 │ │ 36 0.000 58.111 -0.060 │ │ 37 0.000 17.019 -0.060 │ │ 38 0.000 4.746 -0.060 │ │ 39 0.000 5.699 -0.060 │ │ 40 0.439 23.158 0.573 │ │ conditionT.Hpoly.Day10 0 -1.759 12.539 -2.085 │ │ 1 -0.786 26.759 -0.681 │ │ 2 -1.637 12.716 -1.909 │ │ 3 0.000 33.144 0.453 │ │ 4 0.373 14.025 0.991 │ │ 5 0.000 36.924 0.453 │ │ 6 0.000 12.716 0.453 │ │ 7 0.000 55.305 0.453 │ │ 8 0.000 70.166 0.453 │ │ 9 -1.637 14.627 -1.909 │ │ 10 0.000 36.593 0.453 │ │ 11 -0.242 34.808 0.104 │ │ 12 -0.242 10.739 0.104 │ │ 13 0.000 25.403 0.453 │ │ 14 -0.242 36.012 0.104 │ │ 15 -0.242 25.968 0.104 │ │ 16 0.000 49.842 0.453 │ │ 17 0.000 16.994 0.453 │ │ 18 0.000 38.817 0.453 │ │ 19 0.000 46.148 0.453 │ │ 20 -0.242 18.744 0.104 │ │ 21 0.000 24.140 0.453 │ │ 22 -0.242 13.116 0.104 │ │ 23 -1.637 9.496 -1.909 │ │ 24 -1.597 13.038 -1.851 │ │ 25 0.000 20.736 0.453 │ │ 26 -0.242 14.110 0.104 │ │ 27 0.000 19.548 0.453 │ │ 28 -0.242 33.746 0.104 │ │ 29 0.000 10.868 0.453 │ │ 30 0.000 9.601 0.453 │ │ 31 0.000 24.164 0.453 │ │ 32 1.217 29.810 2.209 │ │ 33 0.564 15.377 1.267 │ │ 34 1.186 27.712 2.164 │ │ 35 0.000 17.652 0.453 │ │ 36 -1.716 14.907 -2.023 │ │ 37 0.000 24.285 0.453 │ │ 38 0.000 6.772 0.453 │ │ 39 0.000 8.132 0.453 │ │ 40 0.000 21.303 0.453 │ │ conditionT.Salmonella 0 0.000 34.663 -0.618 │ │ 1 0.000 27.957 -0.618 │ │ 2 0.000 31.114 -0.618 │ │ 3 0.000 15.779 -0.618 │ │ 4 0.000 4.598 -0.618 │ │ 5 0.000 17.578 -0.618 │ │ 6 0.000 6.054 -0.618 │ │ 7 0.000 26.329 -0.618 │ │ 8 0.000 33.404 -0.618 │ │ 9 0.213 44.286 -0.311 │ │ 10 0.000 17.421 -0.618 │ │ 11 0.000 21.108 -0.618 │ │ 12 0.000 6.512 -0.618 │ │ 13 0.000 12.094 -0.618 │ │ 14 2.173 191.842 2.517 │ │ 15 1.547 73.971 1.614 │ │ 16 0.000 23.728 -0.618 │ │ 17 0.000 8.090 -0.618 │ │ 18 0.000 18.480 -0.618 │ │ 19 0.000 21.970 -0.618 │ │ 20 0.000 11.367 -0.618 │ │ 21 0.000 11.492 -0.618 │ │ 22 0.000 7.954 -0.618 │ │ 23 0.000 23.235 -0.618 │ │ 24 0.000 30.651 -0.618 │ │ 25 0.000 9.872 -0.618 │ │ 26 1.547 40.192 1.614 │ │ 27 0.000 9.306 -0.618 │ │ 28 1.547 96.127 1.614 │ │ 29 0.000 5.174 -0.618 │ │ 30 0.000 4.571 -0.618 │ │ 31 0.000 11.504 -0.618 │ │ 32 0.000 4.202 -0.618 │ │ 33 0.000 4.165 -0.618 │ │ 34 0.000 4.030 -0.618 │ │ 35 0.000 8.404 -0.618 │ │ 36 0.000 39.475 -0.618 │ │ 37 0.000 11.561 -0.618 │ │ 38 0.000 3.224 -0.618 │ │ 39 0.000 3.872 -0.618 │ │ 40 0.000 10.142 -0.618 │ └─────────────────────────────────────────────────────────────────────────────────────────────────────────────────┘
┌─────────────────────────────────────────────────────────────────────────────────────────────────────────────────┐ │ Nodes │ ├─────────────────────────────────────────────────────────────────────────────────────────────────────────────────┤ │ Covariate=condition[T.Hpoly.Day10]_node │ ├─────────────────────────────────────────────────────────────────────────────────────────────────────────────────┤ │ Final Parameter Is credible │ │ Node │ │ nsbm_level_4_0 0.00 False │ │ nsbm_level_3_2 0.00 False │ │ nsbm_level_3_0 0.00 False │ │ nsbm_level_3_1 0.00 False │ │ nsbm_level_3_3 -0.24 True │ │ nsbm_level_2_8 0.00 False │ │ nsbm_level_2_10 0.00 False │ │ 10 0.00 False │ │ 31 0.00 False │ │ nsbm_level_2_0 0.00 False │ │ nsbm_level_2_7 0.00 False │ │ nsbm_level_2_11 0.00 False │ │ nsbm_level_2_3 0.00 False │ │ nsbm_level_2_2 -1.64 True │ │ nsbm_level_2_13 0.00 False │ │ nsbm_level_2_1 0.00 False │ │ nsbm_level_2_4 0.00 False │ │ nsbm_level_2_6 0.00 False │ │ nsbm_level_2_14 0.00 False │ │ 11 0.00 False │ │ 16 0.00 False │ │ 37 0.00 False │ │ 19 0.00 False │ │ 27 0.00 False │ │ 30 0.00 False │ │ 0 -1.76 True │ │ 35 0.00 False │ │ 17 0.00 False │ │ 4 0.37 True │ │ 25 0.00 False │ │ 13 0.00 False │ │ 29 0.00 False │ │ 38 0.00 False │ │ 5 0.00 False │ │ 3 0.00 False │ │ 8 0.00 False │ │ 40 0.00 False │ │ 21 0.00 False │ │ 2 0.00 False │ │ 23 0.00 False │ │ 9 0.00 False │ │ 32 2.85 True │ │ 6 0.00 False │ │ 34 1.19 True │ │ 7 0.00 False │ │ 1 -0.79 True │ │ 24 -1.60 True │ │ 18 0.00 False │ │ 36 -1.72 True │ │ 33 0.56 True │ │ 39 0.00 False │ │ 26 0.00 False │ │ 14 0.00 False │ │ 28 0.00 False │ │ 15 0.00 False │ │ 12 0.00 False │ │ 20 0.00 False │ │ 22 0.00 False │ ├─────────────────────────────────────────────────────────────────────────────────────────────────────────────────┤ │ Covariate=condition[T.Hpoly.Day3]_node │ ├─────────────────────────────────────────────────────────────────────────────────────────────────────────────────┤ │ Final Parameter Is credible │ │ Node │ │ nsbm_level_4_0 0.00 False │ │ nsbm_level_3_2 0.00 False │ │ nsbm_level_3_0 0.00 False │ │ nsbm_level_3_1 0.00 False │ │ nsbm_level_3_3 0.00 False │ │ nsbm_level_2_8 0.00 False │ │ nsbm_level_2_10 0.00 False │ │ 10 0.00 False │ │ 31 0.00 False │ │ nsbm_level_2_0 0.00 False │ │ nsbm_level_2_7 0.00 False │ │ nsbm_level_2_11 0.00 False │ │ nsbm_level_2_3 0.44 True │ │ nsbm_level_2_2 -0.26 True │ │ nsbm_level_2_13 0.00 False │ │ nsbm_level_2_1 0.00 False │ │ nsbm_level_2_4 0.00 False │ │ nsbm_level_2_6 0.00 False │ │ nsbm_level_2_14 0.00 False │ │ 11 0.00 False │ │ 16 0.00 False │ │ 37 0.00 False │ │ 19 0.00 False │ │ 27 0.00 False │ │ 30 0.00 False │ │ 0 0.00 False │ │ 35 0.00 False │ │ 17 0.00 False │ │ 4 0.00 False │ │ 25 0.00 False │ │ 13 0.00 False │ │ 29 0.00 False │ │ 38 0.00 False │ │ 5 0.00 False │ │ 3 0.00 False │ │ 8 0.00 False │ │ 40 0.00 False │ │ 21 0.00 False │ │ 2 0.00 False │ │ 23 0.00 False │ │ 9 0.00 False │ │ 32 0.00 False │ │ 6 0.00 False │ │ 34 0.00 False │ │ 7 0.00 False │ │ 1 0.00 False │ │ 24 0.00 False │ │ 18 0.00 False │ │ 36 0.00 False │ │ 33 0.00 False │ │ 39 0.00 False │ │ 26 0.00 False │ │ 14 0.00 False │ │ 28 0.00 False │ │ 15 0.00 False │ │ 12 0.00 False │ │ 20 0.00 False │ │ 22 0.00 False │ ├─────────────────────────────────────────────────────────────────────────────────────────────────────────────────┤ │ Covariate=condition[T.Salmonella]_node │ ├─────────────────────────────────────────────────────────────────────────────────────────────────────────────────┤ │ Final Parameter Is credible │ │ Node │ │ nsbm_level_4_0 0.00 False │ │ nsbm_level_3_2 0.00 False │ │ nsbm_level_3_0 0.00 False │ │ nsbm_level_3_1 0.00 False │ │ nsbm_level_3_3 0.00 False │ │ nsbm_level_2_8 0.00 False │ │ nsbm_level_2_10 0.00 False │ │ 10 0.00 False │ │ 31 0.00 False │ │ nsbm_level_2_0 0.00 False │ │ nsbm_level_2_7 0.00 False │ │ nsbm_level_2_11 0.00 False │ │ nsbm_level_2_3 0.00 False │ │ nsbm_level_2_2 0.00 False │ │ nsbm_level_2_13 0.00 False │ │ nsbm_level_2_1 0.00 False │ │ nsbm_level_2_4 0.00 False │ │ nsbm_level_2_6 1.55 True │ │ nsbm_level_2_14 0.00 False │ │ 11 0.00 False │ │ 16 0.00 False │ │ 37 0.00 False │ │ 19 0.00 False │ │ 27 0.00 False │ │ 30 0.00 False │ │ 0 0.00 False │ │ 35 0.00 False │ │ 17 0.00 False │ │ 4 0.00 False │ │ 25 0.00 False │ │ 13 0.00 False │ │ 29 0.00 False │ │ 38 0.00 False │ │ 5 0.00 False │ │ 3 0.00 False │ │ 8 0.00 False │ │ 40 0.00 False │ │ 21 0.00 False │ │ 2 0.00 False │ │ 23 0.00 False │ │ 9 0.21 True │ │ 32 0.00 False │ │ 6 0.00 False │ │ 34 0.00 False │ │ 7 0.00 False │ │ 1 0.00 False │ │ 24 0.00 False │ │ 18 0.00 False │ │ 36 0.00 False │ │ 33 0.00 False │ │ 39 0.00 False │ │ 26 0.00 False │ │ 14 0.63 True │ │ 28 0.00 False │ │ 15 0.00 False │ │ 12 0.00 False │ │ 20 0.00 False │ │ 22 0.00 False │ └─────────────────────────────────────────────────────────────────────────────────────────────────────────────────┘
再次，tascCODA的接受概率大约在理想值0.85左右，表明优化没有明显问题。
tascCODA的结果首先应解释为对树节点的影响。节点上的非零参数意味着该节点下所有细胞类型的聚合计数显著变化。我们可以在树图中轻松地可视化这三种疾病状态的效果。蓝色圆圈表示增加，红色圆圈表示减少：
In [27]:
Copied!
pt.pl.coda.draw_effects(
tasccoda_data,
modality_key="coda",
tree="tree",
covariate="condition[T.Salmonella]",
show_leaf_effects=False,
show_legend=False,
)
pt.pl.coda.draw_effects(
tasccoda_data,
modality_key="coda",
tree="tree",
covariate="condition[T.Salmonella]",
show_leaf_effects=False,
show_legend=False,
)
Out[27]:
In [28]:
Copied!
pt.pl.coda.draw_effects(
tasccoda_data,
modality_key="coda",
tree="tree",
covariate="condition[T.Hpoly.Day3]",
show_leaf_effects=False,
show_legend=False,
)
pt.pl.coda.draw_effects(
tasccoda_data,
modality_key="coda",
tree="tree",
covariate="condition[T.Hpoly.Day3]",
show_leaf_effects=False,
show_legend=False,
)
Out[28]:
In [29]:
Copied!
pt.pl.coda.draw_effects(
tasccoda_data,
modality_key="coda",
tree="tree",
covariate="condition[T.Hpoly.Day10]",
show_leaf_effects=False,
show_legend=False,
)
pt.pl.coda.draw_effects(
tasccoda_data,
modality_key="coda",
tree="tree",
covariate="condition[T.Hpoly.Day10]",
show_leaf_effects=False,
show_legend=False,
)
Out[29]:
作为替代方案，对内部节点的影响也可以通过树结构转换到细胞类型层面，从而计算出类似于scCODA的对数折叠变化（log-fold changes）。为了可视化细胞类型的对数折叠变化，我们进行与scCODA相同的绘图，灵感来自“高分辨率单细胞图谱揭示了非小细胞肺癌中组织驻留中性粒细胞的多样性和可塑性”{cite}Salcher2022。
In [30]:
Copied!
pt.pl.coda.effects_barplot(tasccoda_data, modality_key="coda", covariates="condition")
pt.pl.coda.effects_barplot(tasccoda_data, modality_key="coda", covariates="condition")
Out[30]:
<seaborn.axisgrid.FacetGrid at 0x19ad2cd90>
Another insightful representation can be gained by plotting the effect sizes for each condition on the UMAP embedding, and comparing it to the cell type assignments:
In [31]:
Copied!
kwargs = {"ncols": 3, "wspace": 0.25, "vcenter": 0, "vmax": 1.5, "vmin": -1.5}
pt.pl.coda.effects_umap(
tasccoda_data,
effect_name=[
"effect_df_condition[T.Salmonella]",
"effect_df_condition[T.Hpoly.Day3]",
"effect_df_condition[T.Hpoly.Day10]",
],
cluster_key="nsbm_level_1",
**kwargs
)
sc.pl.umap(
tasccoda_data["rna"], color=["cell_label", "nsbm_level_1"], ncols=2, wspace=0.5
)
kwargs = {"ncols": 3, "wspace": 0.25, "vcenter": 0, "vmax": 1.5, "vmin": -1.5}
pt.pl.coda.effects_umap(
tasccoda_data,
effect_name=[
"effect_df_condition[T.Salmonella]",
"effect_df_condition[T.Hpoly.Day3]",
"effect_df_condition[T.Hpoly.Day10]",
],
cluster_key="nsbm_level_1",
**kwargs
)
sc.pl.umap(
tasccoda_data["rna"], color=["cell_label", "nsbm_level_1"], ncols=2, wspace=0.5
)
结果与scCODA的发现非常相似：
- 对于沙门氏菌感染，我们在细胞类型聚类中大致代表肠上皮细胞的簇中获得了聚合增加。这种增加在簇12中更为显著，因为在叶级别上有额外的正效应。
- 对于Heligmosomoides polygyrus感染，在感染3天后，我们没有发现可信的变化。10天后，我们观察到包含干细胞和转运扩增细胞的簇减少，以及肠上皮细胞和肠上皮祖细胞的较弱减少，这些变化也被scCODA检测到。
Without labeled clusters¶
并非总是可能或实际使用精确标记的簇（如细胞类型定义），特别是在我们研究细胞类型簇之间的过渡状态（如发育过程）或仅预期感兴趣条件影响细胞类型的一个亚群时。在这种情况下，基于已知注释确定组成变化可能不适用。
一组方法可以检测小于细胞类型簇的细胞亚群中的组成变化，通常从基于相似性的k近邻（KNN）图开始，计算聚类使用的相同低维空间中的相似性：
- DA-seq使用一系列k值计算每个细胞的得分，基于细胞邻域中来自两种生物状态的细胞的相对普遍性{cite}
Zhao2021。这些得分作为逻辑分类器的输入，用于预测每个细胞的生物条件。 - Milo将细胞分配到部分重叠的KNN图中的邻域，然后使用广义线性模型（GLM）进行差异丰度（DA）测试{cite}
Dann2022。 - MELD使用基于图的密度估计计算每个条件下观察到每个细胞的相对似然估计{cite}
Burkhardt2021。
这些方法各有优缺点。由于依赖于逻辑分类，DA-seq设计用于两种生物条件之间的成对比较，但不能用于测试与连续协变量（如年龄或时间点）相关的差异。DA-seq和Milo使用相同条件的重复样本之间的丰度统计量的方差来估计差异丰度的显著性，而MELD不使用此信息。虽然考虑重复样本的一致性可以减少由一个或几个样本驱动的假阳性，但所有基于KNN的方法在感兴趣的条件和混杂因素（由技术或实验变异源定义）强相关时都对信息丢失敏感。在构建KNN图之前使用批处理集成方法和/或在DA测试模型中纳入混杂协变量可以减轻混杂因素的影响，我们将在下面的示例中进一步讨论这一点。需要记住的另一个基于KNN方法的限制是邻域中的细胞可能不一定代表特定的、唯一的生物亚群，因为一个细胞状态可能跨越多个邻域。减少KNN图的k值或在特定谱系的细胞上构建图可以帮助减轻这个问题，确保预测效应对参数选择和使用的数据子集具有鲁棒性{cite}Dann2022。
总的来说，如果在可视化中大簇中明显存在大差异或细胞类型之间的不平衡感兴趣，使用细胞类型感知方法（如scCODA）进行直接分析可能更合适。基于KNN的方法在我们对细胞类型之间的过渡状态或特定细胞类型的特定亚群中出现的细胞丰度差异感兴趣时更为强大。
为了使用Milo进行差异丰度（DA）分析，我们需要构建一个KNN图，以代表细胞之间的生物相似性，就像我们在对单细胞数据集进行聚类或UMAP可视化时所做的那样。这意味着（A）为所有样本构建一个共同的低维空间，（B）最小化由技术因素（即批次效应）驱动的细胞间相似性。
首先，我们使用标准的scanpy工作流程进行降维，以定性评估该数据集中是否存在批次效应。
下面是使用scanpy进行降维分析的代码示例：
In [3]:
Copied!
milo = pt.tl.Milo()
adata = pt.dt.haber_2017_regions()
mdata = milo.load(adata)
mdata
milo = pt.tl.Milo()
adata = pt.dt.haber_2017_regions()
mdata = milo.load(adata)
mdata
Out[3]:
MuData object with n_obs × n_vars = 9842 × 15215
2 modalities
rna: 9842 x 15215
obs: 'batch', 'barcode', 'condition', 'cell_label'
milo: 0 x 0
In [4]:
Copied!
# use logcounts to calculate PCA and neighbors
adata.layers["counts"] = adata.X.copy()
adata.layers["logcounts"] = sc.pp.log1p(adata.layers["counts"]).copy()
adata.X = adata.layers["logcounts"].copy()
sc.pp.highly_variable_genes(
adata, n_top_genes=3000, subset=False
) # 3k genes as used by authors for clustering
sc.pp.pca(adata)
sc.pp.neighbors(adata, n_neighbors=10, n_pcs=30)
sc.tl.umap(adata)
# use logcounts to calculate PCA and neighbors
adata.layers["counts"] = adata.X.copy()
adata.layers["logcounts"] = sc.pp.log1p(adata.layers["counts"]).copy()
adata.X = adata.layers["logcounts"].copy()
sc.pp.highly_variable_genes(
adata, n_top_genes=3000, subset=False
) # 3k genes as used by authors for clustering
sc.pp.pca(adata)
sc.pp.neighbors(adata, n_neighbors=10, n_pcs=30)
sc.tl.umap(adata)
OMP: Info #276: omp_set_nested routine deprecated, please use omp_set_max_active_levels instead.
In [5]:
Copied!
sc.pl.umap(adata, color=["condition", "batch", "cell_label"], ncols=3, wspace=0.25)
sc.pl.umap(adata, color=["condition", "batch", "cell_label"], ncols=3, wspace=0.25)
虽然细胞类型簇大体上被捕获，但我们可以看到不同批次之间的残余分离，即使是同一处理的重复样本。如果我们在这个KNN图上定义邻域，我们可能会有很大一部分邻域仅包含一个或几个批次的细胞。这可能会引入假阴性，尤其是在不同重复样本之间的细胞数量方差过低（例如，所有重复样本为0细胞）或过高（例如，除了一个重复样本有大量细胞，其他所有样本为0细胞）时，还可能引入假阳性，特别是在每个条件的重复样本数量较少的情况下。
为了尽量减少这些错误，我们应用scVI方法来学习批次校正的潜在空间，如集成章节中所介绍的。
In [ ]:
Copied!
import scvi
adata_scvi = adata[:, adata.var["highly_variable"]].copy()
scvi.model.SCVI.setup_anndata(adata_scvi, layer="counts", batch_key="batch")
model_scvi = scvi.model.SCVI(adata_scvi)
max_epochs_scvi = int(np.min([round((20000 / adata.n_obs) * 400), 400]))
model_scvi.train(max_epochs=max_epochs_scvi)
adata.obsm["X_scVI"] = model_scvi.get_latent_representation()
import scvi
adata_scvi = adata[:, adata.var["highly_variable"]].copy()
scvi.model.SCVI.setup_anndata(adata_scvi, layer="counts", batch_key="batch")
model_scvi = scvi.model.SCVI(adata_scvi)
max_epochs_scvi = int(np.min([round((20000 / adata.n_obs) * 400), 400]))
model_scvi.train(max_epochs=max_epochs_scvi)
adata.obsm["X_scVI"] = model_scvi.get_latent_representation()
In [ ]:
Copied!
sc.pp.neighbors(adata, use_rep="X_scVI")
sc.tl.umap(adata)
sc.pp.neighbors(adata, use_rep="X_scVI")
sc.tl.umap(adata)
In [ ]:
Copied!
sc.pl.umap(adata, color=["condition", "batch", "cell_label"], ncols=3, wspace=0.25)
sc.pl.umap(adata, color=["condition", "batch", "cell_label"], ncols=3, wspace=0.25)
通过批次校正，我们可以看到批次之间的混合效果显著改善，细胞标签形成了更加均匀的簇。
批次校正会移除条件之间的生物差异吗？
这实际上归结为良好的实验设计。在理想的设置中，相同条件的重复样本将在不同批次中处理。这允许更准确地估计技术差异，并可能将批次作为混杂因素纳入差异丰度分析的线性模型中（见下文），以进一步减少假阳性。当批次与感兴趣的生物条件混杂时，我们必须认识到，虽然我们可能会减少假阳性，但假阴性的比例也可能增加。分析人员可以根据数据集和差异丰度分析的目的决定哪种类型的错误对分析更有害。
Define neighbourhoods¶
Milo是基于KNN的模型，其中细胞丰度在细胞邻域上进行量化。在Milo中，邻域定义为在无向KNN图中与同一细胞（索引细胞）连接的细胞组。虽然我们原则上可以为图中的每个细胞设置一个邻域，但这将效率低下并显著增加多重检验的负担。因此，Milo从一个随机抽样的一部分细胞开始，抽取一组细化的细胞作为邻域的索引细胞。初始比例可以使用milo.make_nhoods函数中的prop参数指定。默认情况下，我们建议使用prop=0.1（10%的细胞），并在大数据集（> 10万细胞）上减少到5%或2%以提高可扩展性。
如果未指定neighbors_key参数，Milo将使用.obsp中的邻居。因此，请确保在正确的表示（即如果需要批次校正，则为集成的潜在空间）上运行sc.pp.neighbors。
In [ ]:
Copied!
milo.make_nhoods(mdata, prop=0.1)
milo.make_nhoods(mdata, prop=0.1)
现在，细胞到邻域的二元分配存储在adata.obsm['nhoods']中。我们可以看到，正如预期的那样，邻域的数量应该小于或等于图中细胞数量乘以prop参数。在这种情况下，邻域的数量应小于或等于984。
In [ ]:
Copied!
adata.obsm["nhoods"]
adata.obsm["nhoods"]
Out[ ]:
<9842x847 sparse matrix of type '<class 'numpy.float32'>' with 22864 stored elements in Compressed Sparse Row format>
此时，我们需要检查每个邻域中的细胞数量中位数，以确保邻域包含足够的细胞以检测样本之间的差异。
下面是如何检查每个邻域中的细胞数量中位数的示例代码：
In [ ]:
Copied!
nhood_size = adata.obsm["nhoods"].toarray().sum(0)
plt.hist(nhood_size, bins=20)
plt.xlabel("# cells in neighbourhood")
plt.ylabel("# neighbouthoods")
nhood_size = adata.obsm["nhoods"].toarray().sum(0)
plt.hist(nhood_size, bins=20)
plt.xlabel("# cells in neighbourhood")
plt.ylabel("# neighbouthoods")
In [ ]:
Copied!
np.median(nhood_size)
np.median(nhood_size)
Out[ ]:
26.0
我们预计每个邻域中的最小细胞数量应该等于图构建过程中使用的k参数（在这种情况下为k=10）。为了增加DA测试的统计效力，我们需要在大多数邻域中包含来自所有样本的足够数量的细胞。以下是一个经验法则：为了在一个邻域中每个样本有3个细胞的中位数，邻域中的细胞数量应该至少是样本数量的3倍。在这种情况下，我们有10个样本。如果我们希望每个邻域中平均有3个来自每个样本的细胞，则最小细胞数量应为30。
基于上述绘图，我们有大量邻域的细胞数少于30，这可能导致统计效力不足的测试。为了解决这个问题，我们只需要使用n_neighbors=30重新计算KNN图。为了区分用于邻域级别DA分析的KNN图和用于UMAP构建的图，我们将其存储为adata.obsp中的一个独立图。
下面是重新计算KNN图的示例代码：
In [ ]:
Copied!
sc.pp.neighbors(adata, n_neighbors=30, use_rep="X_scVI", key_added="milo")
milo.make_nhoods(mdata, neighbors_key="milo", prop=0.1)
sc.pp.neighbors(adata, n_neighbors=30, use_rep="X_scVI", key_added="milo")
milo.make_nhoods(mdata, neighbors_key="milo", prop=0.1)
Let's check that the distribution of neighbourhood sizes has shifted.
In [ ]:
Copied!
nhood_size = adata.obsm["nhoods"].toarray().sum(0)
plt.hist(nhood_size, bins=20)
plt.xlabel("# cells in neighbourhood")
plt.ylabel("# neighbouthoods")
nhood_size = adata.obsm["nhoods"].toarray().sum(0)
plt.hist(nhood_size, bins=20)
plt.xlabel("# cells in neighbourhood")
plt.ylabel("# neighbouthoods")
Count cells in neighbourhoods¶
In the next step, Milo counts cells belonging to each of the samples (here identified by the batch column in adata.obs).
In [ ]:
Copied!
milo.count_nhoods(mdata, sample_col="batch")
milo.count_nhoods(mdata, sample_col="batch")
Out[ ]:
MuData object with n_obs × n_vars = 9842 × 15215
2 modalities
rna: 9842 x 15215
obs: 'batch', 'barcode', 'condition', 'cell_label', 'nhood_ixs_random', 'nhood_ixs_refined', 'nhood_kth_distance'
var: 'highly_variable', 'means', 'dispersions', 'dispersions_norm'
uns: 'hvg', 'pca', 'neighbors', 'umap', 'condition_colors', 'batch_colors', 'cell_label_colors', 'nhood_neighbors_key', 'milo'
obsm: 'X_pca', 'X_umap', 'X_scVI', 'nhoods'
varm: 'PCs'
layers: 'counts', 'logcounts'
obsp: 'distances', 'connectivities', 'milo_distances', 'milo_connectivities'
milo_compositional: 10 x 808
var: 'index_cell', 'kth_distance'
uns: 'sample_col'
这会存储一个邻域级别的AnnData对象，其中nhood_adata.X存储每个样本在每个邻域中的细胞数量。
In [ ]:
Copied!
mdata["milo"]
mdata["milo"]
Out[ ]:
AnnData object with n_obs × n_vars = 10 × 808
var: 'index_cell', 'kth_distance'
uns: 'sample_col'
我们可以验证每个样本的平均细胞数量乘以样本数量大致对应于一个邻域中的细胞数量。
In [ ]:
Copied!
mean_n_cells = mdata["milo"].X.toarray().mean(0)
plt.plot(nhood_size, mean_n_cells, ".")
plt.xlabel("# cells in nhood")
plt.ylabel("Mean # cells per sample in nhood")
mean_n_cells = mdata["milo"].X.toarray().mean(0)
plt.plot(nhood_size, mean_n_cells, ".")
plt.xlabel("# cells in nhood")
plt.ylabel("Mean # cells per sample in nhood")
Run differential abundance test on neighbourhoods¶
Milo使用edgeR的QLF测试来检验在每个邻域中感兴趣条件下细胞数量是否存在统计显著差异。
在这里，我们感兴趣的是检测在感染响应中哪些邻域的细胞数量显著增加或减少。由于condition协变量存储了许多不同类型的感染，我们需要指定在差异丰度测试中需要对比的条件（遵循R中使用的惯例，默认情况下将使用协变量的最后一个级别与其余级别进行对比，在本例中为Salmonella与其他条件）。要指定比较，我们使用GLM在R中的语法。
首先测试与沙门氏菌感染相关的差异：
In [ ]:
Copied!
milo.da_nhoods(
mdata, design="~condition", model_contrasts="conditionSalmonella-conditionControl"
)
milo_results_salmonella = mdata["milo"].obs.copy()
milo_results_salmonella
milo.da_nhoods(
mdata, design="~condition", model_contrasts="conditionSalmonella-conditionControl"
)
milo_results_salmonella = mdata["milo"].obs.copy()
milo_results_salmonella
Out[ ]:
| condition | batch | |
|---|---|---|
| B1 | Control | B1 |
| B2 | Control | B2 |
| B3 | Control | B3 |
| B4 | Control | B4 |
| B5 | Hpoly.Day3 | B5 |
| B6 | Hpoly.Day3 | B6 |
| B7 | Hpoly.Day10 | B7 |
| B8 | Hpoly.Day10 | B8 |
| B9 | Salmonella | B9 |
| B10 | Salmonella | B10 |
对于每个邻域，我们计算一组统计量。最重要的是：
- log-Fold Change (logFC)： 这表示细胞丰度差异的效应大小，对应于GLM中与感兴趣条件相关的系数。如果logFC > 0，表示邻域中富含感兴趣条件下的细胞；如果logFC < 0，表示邻域中感兴趣条件下的细胞减少。
- 未校正的p值 (PValue)： 这是QLF测试的p值，未进行多重检验校正。
- 空间FDR (SpatialFDR)： 这是调整后的p值，用于限制假发现率。计算方法是改编自Lun等人引入的加权Benjamini-Hochberg (BH)校正{cite}
lun2017，考虑到邻域是部分重叠的（即一个细胞可以属于多个邻域），因此不同邻域的DA测试并不是完全独立的。实际上，BH校正的权重是与k-最近邻到索引细胞的距离的倒数（存储在kth_distance中），这被用作与其他邻域重叠量的代理。您可能会注意到，SpatialFDR值总是低于或等于使用传统BH校正计算的FDR值。
在进行任何结果的探索和解释之前，我们可以通过一组诊断图来可视化这些统计数据，以验证我们的统计测试。
In [ ]:
Copied!
def plot_milo_diagnostics(mdata):
alpha = 0.1 ## significance threshold
with matplotlib.rc_context({"figure.figsize": [12, 12]}):
## Check P-value histogram
plt.subplot(2, 2, 1)
plt.hist(mdata["milo"].var["PValue"], bins=20)
plt.xlabel("Uncorrected P-value")
## Visualize extent of multiple-testing correction
plt.subplot(2, 2, 2)
plt.scatter(
mdata["milo"].var["PValue"],
mdata["milo"].var["SpatialFDR"],
s=3,
)
plt.xlabel("Uncorrected P-value")
plt.ylabel("SpatialFDR")
## Visualize volcano plot
plt.subplot(2, 2, 3)
plt.scatter(
mdata["milo"].var["logFC"],
-np.log10(mdata["milo"].var["SpatialFDR"]),
s=3,
)
plt.axhline(
y=-np.log10(alpha),
color="red",
linewidth=1,
label=f"{int(alpha*100)} % SpatialFDR",
)
plt.legend()
plt.xlabel("log-Fold Change")
plt.ylabel("- log10(SpatialFDR)")
plt.tight_layout()
## Visualize MA plot
df = mdata["milo"].var
emp_null = df[df["SpatialFDR"] >= alpha]["logFC"].mean()
df["Sig"] = df["SpatialFDR"] < alpha
plt.subplot(2, 2, 4)
sns.scatterplot(data=df, x="logCPM", y="logFC", hue="Sig")
plt.axhline(y=0, color="grey", linewidth=1)
plt.axhline(y=emp_null, color="purple", linewidth=1)
plt.legend(title=f"< {int(alpha*100)} % SpatialFDR")
plt.xlabel("Mean log-counts")
plt.ylabel("log-Fold Change")
plt.show()
plot_milo_diagnostics(mdata)
def plot_milo_diagnostics(mdata):
alpha = 0.1 ## significance threshold
with matplotlib.rc_context({"figure.figsize": [12, 12]}):
## Check P-value histogram
plt.subplot(2, 2, 1)
plt.hist(mdata["milo"].var["PValue"], bins=20)
plt.xlabel("Uncorrected P-value")
## Visualize extent of multiple-testing correction
plt.subplot(2, 2, 2)
plt.scatter(
mdata["milo"].var["PValue"],
mdata["milo"].var["SpatialFDR"],
s=3,
)
plt.xlabel("Uncorrected P-value")
plt.ylabel("SpatialFDR")
## Visualize volcano plot
plt.subplot(2, 2, 3)
plt.scatter(
mdata["milo"].var["logFC"],
-np.log10(mdata["milo"].var["SpatialFDR"]),
s=3,
)
plt.axhline(
y=-np.log10(alpha),
color="red",
linewidth=1,
label=f"{int(alpha*100)} % SpatialFDR",
)
plt.legend()
plt.xlabel("log-Fold Change")
plt.ylabel("- log10(SpatialFDR)")
plt.tight_layout()
## Visualize MA plot
df = mdata["milo"].var
emp_null = df[df["SpatialFDR"] >= alpha]["logFC"].mean()
df["Sig"] = df["SpatialFDR"] < alpha
plt.subplot(2, 2, 4)
sns.scatterplot(data=df, x="logCPM", y="logFC", hue="Sig")
plt.axhline(y=0, color="grey", linewidth=1)
plt.axhline(y=emp_null, color="purple", linewidth=1)
plt.legend(title=f"< {int(alpha*100)} % SpatialFDR")
plt.xlabel("Mean log-counts")
plt.ylabel("log-Fold Change")
plt.show()
plot_milo_diagnostics(mdata)
- P值直方图显示了多重检验校正前的P值分布。根据定义，我们预计在零假设下的P值（>显著性水平）是均匀分布的，而接近零的P值峰值表示显著结果。这可以让你了解测试的保守程度，并可能帮助及早发现一些病理情况。例如，如果P值的分布看起来是双峰的，第二个峰值接近1，这可能表明你有大量邻域在一个条件的重复样本之间没有方差（例如，一个条件的所有重复样本都有0个细胞），这可能表明存在残留的批次效应或需要增加邻域的大小；如果P值直方图向左倾斜，这可能表明模型中未考虑混杂协变量。有关其他病理情况和可能的解释，请参见这篇博客文章。
- 对于每个邻域，我们绘制未经校正的P值与控制空间FDR的P值。这里我们预计调整后的P值会更大（即点在对角线以上）。如果FDR校正特别严格（即许多值接近1），这可能表明病理情况。你可能在测试太多邻域（可以在
milo.make_nhoods中减少prop）或邻域之间的重叠过多（构建KNN图时可能需要减小_k_）。 - 火山图给我们一个关于多重检验校正后有多少邻域显示显著DA的想法（-log(SpatialFDR) > 1），并显示有多少邻域富含或缺少感兴趣条件下的细胞。
- MA图显示每个样本的平均细胞数与测试的log-Fold Change之间的依赖关系。在平衡情况下，我们预计点集中在logFC=0左右，否则偏移可能表明来自不同条件样本之间的平均细胞数存在严重不平衡。有关如何解释MA图的更多提示，请参见https://github.com/MarioniLab/miloR/issues/208。
在进行合理性检查后，我们可以通过索引细胞在UMAP嵌入上的位置来可视化每个邻域的DA结果，以定性评估哪些细胞类型可能受感染影响最大。
In [ ]:
Copied!
milo.build_nhood_graph(mdata)
with matplotlib.rc_context({"figure.figsize": [10, 10]}):
pt.pl.milo.nhood_graph(mdata, alpha=0.1, min_size=5, plot_edges=False)
sc.pl.umap(mdata["rna"], color="cell_label", legend_loc="on data")
milo.build_nhood_graph(mdata)
with matplotlib.rc_context({"figure.figsize": [10, 10]}):
pt.pl.milo.nhood_graph(mdata, alpha=0.1, min_size=5, plot_edges=False)
sc.pl.umap(mdata["rna"], color="cell_label", legend_loc="on data")
This shows a set of neighbourhoods enriched upon Salmonella infection corresponding to mature enterocytes, and a depletion in a subset of stem cell neighbourhoods. For interpretation of results, it's often useful to annotate neighbourhoods by the cell type cluster that they overlap with.
In [ ]:
Copied!
milo.annotate_nhoods(mdata, anno_col="cell_label")
# Define as mixed if fraction of cells in nhood with same label is lower than 0.75
mdata["milo"].var.loc[
mdata["milo"].var["nhood_annotation_frac"] < 0.75, "nhood_annotation"
] = "Mixed"
milo.annotate_nhoods(mdata, anno_col="cell_label")
# Define as mixed if fraction of cells in nhood with same label is lower than 0.75
mdata["milo"].var.loc[
mdata["milo"].var["nhood_annotation_frac"] < 0.75, "nhood_annotation"
] = "Mixed"
In [ ]:
Copied!
pt.pl.milo.da_beeswarm(mdata)
plt.show()
pt.pl.milo.da_beeswarm(mdata)
plt.show()
那组成效应呢？
将Milo结果与scCODA结果进行比较，我们在沙门氏菌感染后发现了肠上皮细胞的强富集，同时在一部分干细胞中也发现了减少，这与原作者报道的情况相似{cite}comp:Haber2017。尽管我们没有真实数据来验证干细胞丰度的减少是否真实，但需要注意的是，Milo中的GLM并未明确建模邻域中细胞丰度的组成特性，因此理论上结果可能会受到组成偏差的影响。实际上，在大量邻域上进行测试缓解了这一问题，因为相反方向的效应分布在数千个邻域而不是数十种细胞类型中。此外，Milo中使用的测试使用了修剪平均M值归一化方法（TMM归一化{cite}comp:Robinson2010）来估计对样本间组成差异具有鲁棒性的归一化因子。在这个特定的示例中，残留的组成效应可能可以用以下因素解释：（A）邻域数量相对较少（< 1000），（B）肠上皮细胞邻域中的效应量非常大，或（C）每个条件的重复样本数量非常少。
值得注意的是，Milo使用的GLM框架允许测试细胞的富集/减少，也适用于连续协变量。我们通过测试_Heligmosomoides polygyrus_感染时间过程中的差异丰度来演示这一点。
In [ ]:
Copied!
## Turn into continuous variable
mdata["rna"].obs["Hpoly_timecourse"] = (
mdata["rna"]
.obs["condition"]
.cat.reorder_categories(["Salmonella", "Control", "Hpoly.Day3", "Hpoly.Day10"])
)
mdata["rna"].obs["Hpoly_timecourse"] = mdata["rna"].obs["Hpoly_timecourse"].cat.codes
## Here we exclude salmonella samples
test_samples = (
mdata["rna"]
.obs.batch[mdata["rna"].obs.condition != "Salmonella"]
.astype("str")
.unique()
)
milo.da_nhoods(mdata, design="~ Hpoly_timecourse", subset_samples=test_samples)
## Turn into continuous variable
mdata["rna"].obs["Hpoly_timecourse"] = (
mdata["rna"]
.obs["condition"]
.cat.reorder_categories(["Salmonella", "Control", "Hpoly.Day3", "Hpoly.Day10"])
)
mdata["rna"].obs["Hpoly_timecourse"] = mdata["rna"].obs["Hpoly_timecourse"].cat.codes
## Here we exclude salmonella samples
test_samples = (
mdata["rna"]
.obs.batch[mdata["rna"].obs.condition != "Salmonella"]
.astype("str")
.unique()
)
milo.da_nhoods(mdata, design="~ Hpoly_timecourse", subset_samples=test_samples)
In [ ]:
Copied!
plot_milo_diagnostics(mdata)
plot_milo_diagnostics(mdata)
In [ ]:
Copied!
with matplotlib.rc_context({"figure.figsize": [10, 10]}):
pt.pl.milo.nhood_graph(mdata, alpha=0.1, min_size=5, plot_edges=False)
with matplotlib.rc_context({"figure.figsize": [10, 10]}):
pt.pl.milo.nhood_graph(mdata, alpha=0.1, min_size=5, plot_edges=False)
In [ ]:
Copied!
pt.pl.milo.da_beeswarm(mdata)
plt.show()
pt.pl.milo.da_beeswarm(mdata)
plt.show()
我们可以通过绘制在检测到显著富集或耗尽的区域中，按条件每个样本的细胞数量，来验证该测试是否捕获了时间过程中细胞数量的线性增加。
In [ ]:
Copied!
entero_ixs = mdata["milo"].var_names[
(mdata["milo"].var["SpatialFDR"] < 0.1)
& (mdata["milo"].var["logFC"] < 0)
& (mdata["milo"].var["nhood_annotation"] == "Enterocyte")
]
plt.title("Enterocyte")
pt.pl.milo.nhood_counts_by_cond(
mdata, test_var="Hpoly_timecourse", subset_nhoods=entero_ixs
)
plt.show()
tuft_ixs = mdata["milo"].var_names[
(mdata["milo"].var["SpatialFDR"] < 0.1)
& (mdata["milo"].var["logFC"] > 0)
& (mdata["milo"].var["nhood_annotation"] == "Tuft")
]
plt.title("Tuft cells")
pt.pl.milo.nhood_counts_by_cond(
mdata, test_var="Hpoly_timecourse", subset_nhoods=tuft_ixs
)
plt.show()
entero_ixs = mdata["milo"].var_names[
(mdata["milo"].var["SpatialFDR"] < 0.1)
& (mdata["milo"].var["logFC"] < 0)
& (mdata["milo"].var["nhood_annotation"] == "Enterocyte")
]
plt.title("Enterocyte")
pt.pl.milo.nhood_counts_by_cond(
mdata, test_var="Hpoly_timecourse", subset_nhoods=entero_ixs
)
plt.show()
tuft_ixs = mdata["milo"].var_names[
(mdata["milo"].var["SpatialFDR"] < 0.1)
& (mdata["milo"].var["logFC"] > 0)
& (mdata["milo"].var["nhood_annotation"] == "Tuft")
]
plt.title("Tuft cells")
pt.pl.milo.nhood_counts_by_cond(
mdata, test_var="Hpoly_timecourse", subset_nhoods=tuft_ixs
)
plt.show()
有趣的是，在邻域上进行的差异丰度（DA）测试检测到在感染后，在Tuft细胞和部分杯状细胞的子集中有丰度增加。我们可以通过检查邻域中细胞的平均基因表达谱来表征感染后富集的细胞类型亚群之间的差异。例如，如果我们考察杯状细胞的邻域，我们可以看到感染后丰度增加的邻域显示出更高的Retnlb表达，这是一种与抗寄生虫免疫相关的基因【引用：Haber2017】。
In [ ]:
Copied!
## Compute average Retnlb expression per neighbourhood
# (you can add mean expression for all genes using milo.utils.add_nhood_expression)
mdata["rna"].obs["Retnlb_expression"] = (
mdata["rna"][:, "Retnlb"].layers["logcounts"].toarray().ravel()
)
milo.annotate_nhoods_continuous(mdata, "Retnlb_expression")
# milo.annotate_nhoods(mdata, "Retnlb_expression")
## Subset to Goblet cell neighbourhoods
nhood_df = mdata["milo"].var.copy()
nhood_df = nhood_df[nhood_df["nhood_annotation"] == "Goblet"]
sns.scatterplot(data=nhood_df, x="logFC", y="nhood_Retnlb_expression")
plt.show()
## Compute average Retnlb expression per neighbourhood
# (you can add mean expression for all genes using milo.utils.add_nhood_expression)
mdata["rna"].obs["Retnlb_expression"] = (
mdata["rna"][:, "Retnlb"].layers["logcounts"].toarray().ravel()
)
milo.annotate_nhoods_continuous(mdata, "Retnlb_expression")
# milo.annotate_nhoods(mdata, "Retnlb_expression")
## Subset to Goblet cell neighbourhoods
nhood_df = mdata["milo"].var.copy()
nhood_df = nhood_df[nhood_df["nhood_annotation"] == "Goblet"]
sns.scatterplot(data=nhood_df, x="logFC", y="nhood_Retnlb_expression")
plt.show()
考虑混杂协变量： 除了我们感兴趣的条件外，一些混杂因素可能会影响细胞的丰度和比例。例如，不同的样本集可能在同一批次中被处理或测序，或者一组样本可能包含使用不同标记进行FAC排序以丰富感兴趣的细胞群的细胞。只要这些因素与感兴趣的条件不完全相关，我们就可以在用于差异丰度测试的模型中包括这些协变量，以估计与感兴趣条件相关的差异丰度，同时最小化由混杂因素解释的差异。在Milo中，我们可以使用语法 ~ confounder + condition 来表达这种测试设计。
In [ ]:
Copied!
## Make dummy confounder for the sake of this example
np.random.seed(42)
nhood_adata = mdata["milo"].copy()
conf_dict = dict(
zip(
nhood_adata.obs_names,
np.random.choice(["group1", "group2"], nhood_adata.n_obs),
)
)
mdata["rna"].obs["dummy_confounder"] = [conf_dict[x] for x in mdata["rna"].obs["batch"]]
milo.da_nhoods(mdata, design="~ dummy_confounder+condition")
## Make dummy confounder for the sake of this example
np.random.seed(42)
nhood_adata = mdata["milo"].copy()
conf_dict = dict(
zip(
nhood_adata.obs_names,
np.random.choice(["group1", "group2"], nhood_adata.n_obs),
)
)
mdata["rna"].obs["dummy_confounder"] = [conf_dict[x] for x in mdata["rna"].obs["batch"]]
milo.da_nhoods(mdata, design="~ dummy_confounder+condition")
In [ ]:
Copied!
mdata["milo"].var
mdata["milo"].var
Out[ ]:
| index_cell | kth_distance | SpatialFDR | Sig | Nhood_size | nhood_annotation | nhood_annotation_frac | nhood_Retnlb_expression | logFC | logCPM | F | PValue | FDR | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | B1_AAAGGCCTAAGGCG_Control_Stem | 1.304513 | 0.056105 | False | 53.0 | Stem | 0.830189 | 0.033807 | -3.696119 | 10.690300 | 9.083460 | 0.002595 | 0.066143 |
| 1 | B1_AACACGTGATGCTG_Control_TA.Early | 1.335187 | 0.938353 | False | 67.0 | Mixed | 0.477612 | 0.020691 | -0.248959 | 10.926409 | 0.078934 | 0.778762 | 0.941976 |
| 2 | B1_AACTTGCTGGTATC_Control_Enterocyte | 1.519376 | 0.693653 | False | 49.0 | Enterocyte | 1.000000 | 0.000000 | 0.951949 | 10.727155 | 1.416844 | 0.233993 | 0.720537 |
| 3 | B1_AAGAACGATGACTG_Control_Enterocyte | 2.143153 | 0.746709 | False | 39.0 | Enterocyte | 1.000000 | 0.000000 | 0.879631 | 10.467676 | 1.109896 | 0.292168 | 0.769131 |
| 4 | B1_AATTACGAAACAGA_Control_Enterocyte.Progenitor | 1.600587 | 0.436180 | False | 37.0 | Enterocyte.Progenitor | 0.945946 | 0.000000 | -2.440105 | 10.296494 | 3.202427 | 0.073604 | 0.478744 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 803 | B10_TTAGGTCTAGACTC_Salmonella_Goblet | 1.547428 | 0.400895 | False | 48.0 | Goblet | 1.000000 | 0.126426 | 1.931002 | 10.566431 | 3.591423 | 0.058150 | 0.443255 |
| 804 | B10_TTAGTCACCATGGT_Salmonella_TA.Early | 1.348982 | 0.880493 | False | 64.0 | TA.Early | 0.875000 | 0.010830 | -0.553709 | 10.876626 | 0.342947 | 0.558166 | 0.886244 |
| 805 | B10_TTATGGCTTAACGC_Salmonella_TA.Early | 1.357123 | 0.981884 | False | 51.0 | TA.Early | 0.862745 | 0.000000 | 0.071987 | 10.649724 | 0.007052 | 0.933080 | 0.982928 |
| 806 | B10_TTCATCGACCGTAA_Salmonella_TA.Early | 1.313244 | 0.908718 | False | 66.0 | TA.Early | 0.787879 | 0.021004 | -0.403998 | 10.825716 | 0.176318 | 0.674579 | 0.916060 |
| 807 | B10_TTGAACCTCATTTC_Salmonella_TA.Early | 1.333960 | 0.787177 | False | 55.0 | Mixed | 0.454545 | 0.012603 | 0.774925 | 10.712952 | 0.811296 | 0.367791 | 0.805382 |
808 rows × 13 columns
Key Takeaways¶
- 如果主要兴趣在于已知细胞类型或状态之间的组成变化，可以使用scCODA或tascCODA来统计评估丰度变化。
- 如果数据不明显聚类，例如在发育过程中，或者我们对可能出现在细胞类型之间过渡状态或某个给定细胞类型的特定子集中的细胞丰度差异感兴趣，则应使用基于KNN的方法如DA-Seq或MILO。
Quiz¶
- It is tricky to deduce compositional changes visually. Why?
- Why is it necessary to interpret cell type abundances as proportions instead of absolute counts? What are the dangers of not doing so?
- In which cases should tools that use cluster information, such as cell types be used, and in which cases tools that do not use cluster information?